多维激励下大跨上承式铁路钢桁拱桥空间地震响应

2020-10-17

中国铁道科学 2020年5期

（兰州交通大学土木工程学院，甘肃兰州 730070）

地震具有很强的随机性。地震发生时，不仅大小是随机的，方向也是随机的［1］。在地震响应分析过程中，需选择最不利的方向来施加地震动［2］。理论研究和震害经验均表明，地震时的地面运动是复杂的多维运动，严格来说有3 个平动分量和3 个转动分量［3-4］。目前对地震转动分量的观测资料还很少，地震响应分析时无法考虑。大跨度拱桥结构复杂，动力特性具有一定的空间耦合特性，地震响应分析时仅考虑一维地震作用是不够的，应该考虑多维地震动的联合作用。

关于地震动激励方式对拱桥地震响应影响的研究已有诸多成果。文献［5-6］采用4 种不同的地震动激励方式（纵向、横向及竖向单独输入与3个方向同时输入）分析了上承式简单体系钢筋混凝土拱桥、下承式钢管混凝土刚架系杆拱桥和钢筋混凝土箱板拱桥的地震响应特点。文献［7］采用单向及双向地震动输入模式分析了行波效应对重庆朝天门长江大桥（中承式连续钢桁架系杆拱桥）地震响应的影响。文献［8］采用欧洲规范［9］中的地震动激励组合方式对南京大胜关大桥进行了一致激励下的地震响应分析。文献［10］以中承式钢拱桥为研究对象，分析了纵+竖、纵+横+竖向地震动输入下钢拱桥的损伤发展情况。文献［11］以1 座上承式钢桁架拱桥为研究对象，分析了在纵向、横向和双向（横向+纵向）地震动输入下大跨度钢拱桥的损伤状态。文献［12］研究了几何非线性和材料非线性效应对上承式两铰钢拱桥地震响应的影响。从既有的文献看，研究对象多侧重钢筋混凝土拱桥或梁拱组合式等无推力拱桥，对钢桁拱桥主要研究其构件强度进入非线性后的损伤机理。但对结构复杂、杆件众多、振型密集及空间地震响应耦合显著的大跨度上承式钢桁拱桥的地震响应受力特征，即拱肋各内力分量分布特征，空间耦联效应研究较少。

本文以某490 m 大跨上承式铁路钢桁拱桥为研究对象，运用SAP2000 软件，进行1 维、2 维及3维地震动激励下大跨钢桁拱桥地震响应研究。

1 工程背景及全桥动力计算模型

某铁路上承式钢桁拱桥，如图1所示，其跨度为490 m，拱轴线采用拱轴系数2.0 的悬链线，矢跨比为1/4.475。拱肋采用提篮拱结构形式，拱肋内倾3.65°，4 片桁拱设计，每2 片构成1 肋，每肋2片主桁中心距为3.4 m，并通过横撑连接成整体。2 片拱肋中心距在拱脚处为32 m，拱顶处为18 m。桁拱采用变高度桁高，拱顶桁高为11 m，拱脚为16 m。上、下弦杆采用箱形截面，梁高、宽均为2.0 m。主拱圈及腹杆采用Q370q，主桁联结系采用Q345q，拱上立柱及钢箱梁采用Q345q，交界墩为钢筋混凝土桥墩。主桥拱座采用分离式嵌固基础。桥址区工程场地类别为Ⅱ类，地震动峰值加速度为0.248g（g为重力加速度），地震动响应谱周期为0.45 s。

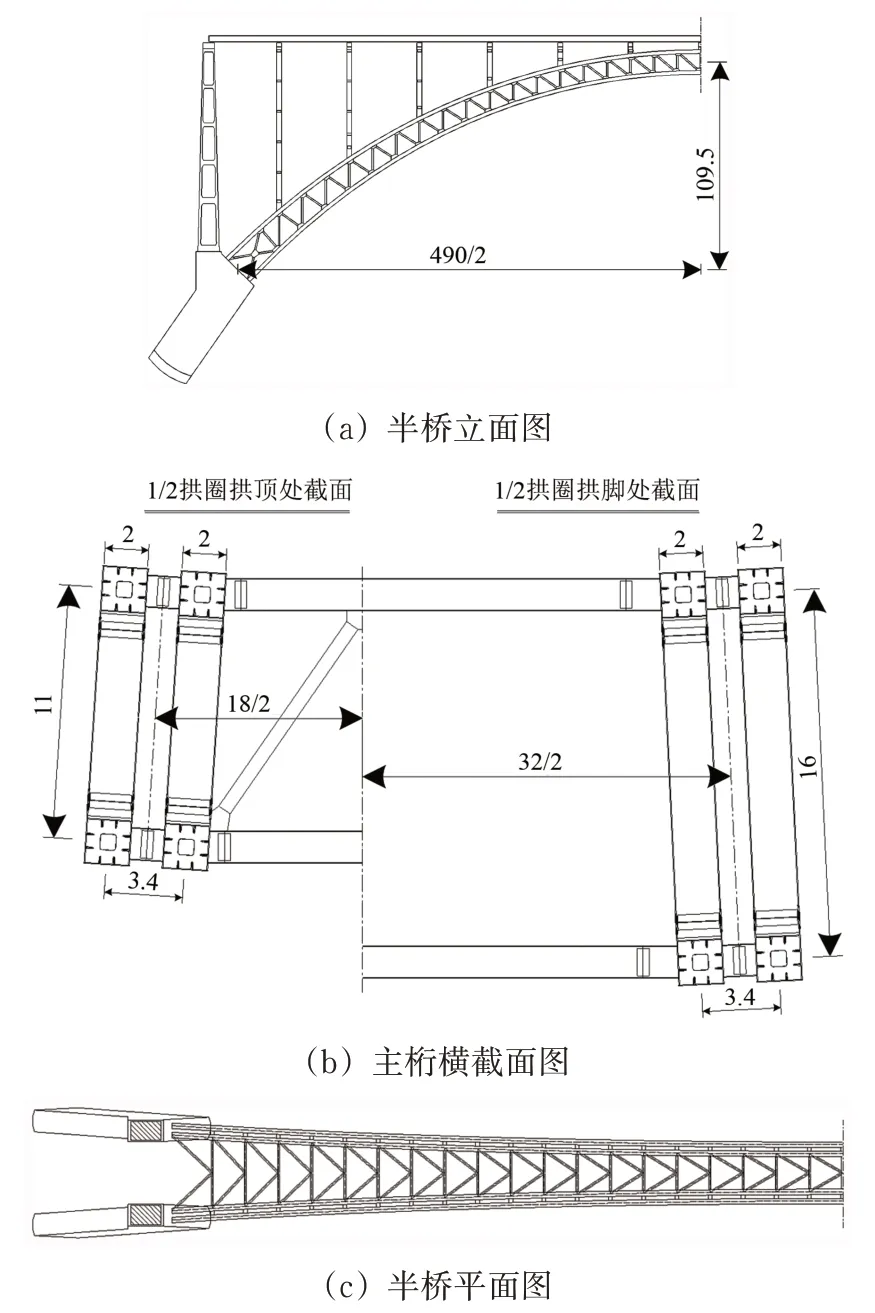
图1 大跨钢桁拱桥结构布置（单位：m）

依据该桥的结构特征，采用有限元软件SAP2000建立全桥有限元模型，如图2所示。主拱肋、拱上立柱、钢箱梁、交界墩均采用空间梁单元模拟；拱上立柱与主梁之间、交界墩与主梁间设置的支座采用自由度耦合方式模拟，交界墩墩底及拱脚均固结。模型总共1 040个节点、2 060个单元。

图2 全桥动力计算模型

根据桥址区场地特征，从太平洋地震工程研究中心（PEER 网站）地震动数据库选取有代表性的EL-centro 波（峰值加速度为341.7 cm·s-2，场地特征周期为0.55 s）及Taft 波（峰值加速度为175.9 cm·s-2，场地特征周期为0.44 s）作为纵向、横向、竖向输入地震动，并将EL-centro 波及Taft 波峰值均调整为0.248g，调幅后EL-centro 波及Taft波加速度时程如图3和图4所示。

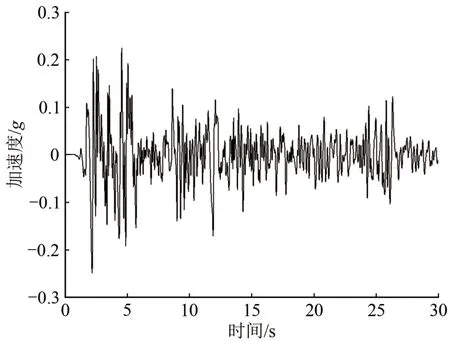
图3 EL-centro波加速度时程

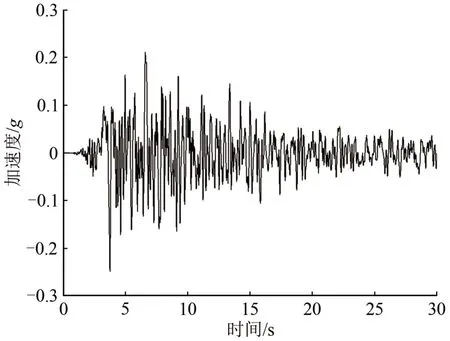
图4 Taft波加速度时程

2 大跨上承式钢拱桥地震响应的空间耦联性

考虑1 维地震动激励，分别沿纵向、横向及竖向输入，对大跨钢桁拱桥进行一致激励下地震响应分析。为了便于表达结构内力的空间耦联特性，引入结构内力空间耦联系数对结构内力进行无量纲化处理。当讨论轴力、面内弯矩时，空间耦联系数定义为横向或竖向输入引起的内力最大绝对值与纵向输入引起的内力最大绝对值比；当讨论面外弯矩时，空间耦联系数定义为纵向或竖向输入引起的内力最大绝对值与横向输入引起的内力最大绝对值比。在单向地震动激励下，由于结构的对称性，结构响应最大绝对值也满足对称性。EL-centro 波、Taft波激励下，拱肋上、下弦杆的内力空间耦联系数分析结果分别见表1和表2。

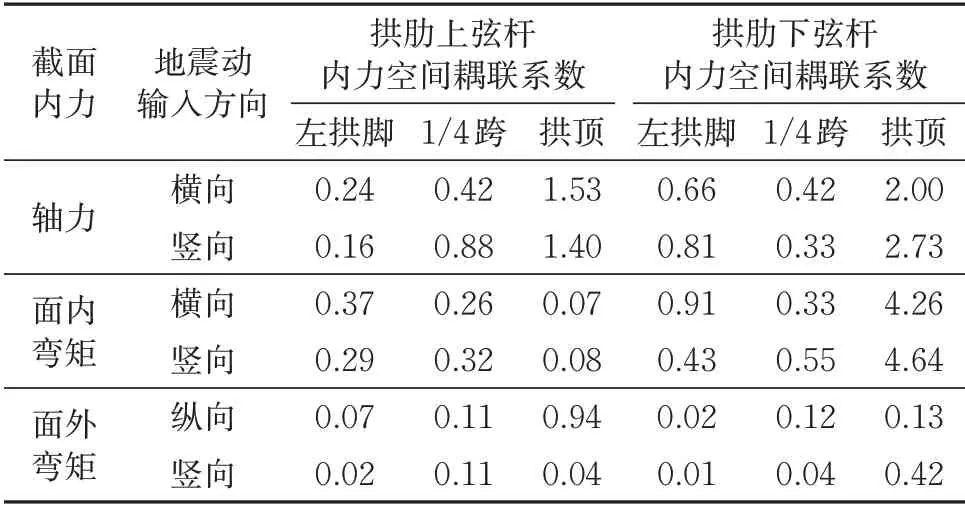
表1 EL-centro波激励下结构内力空间耦联系数

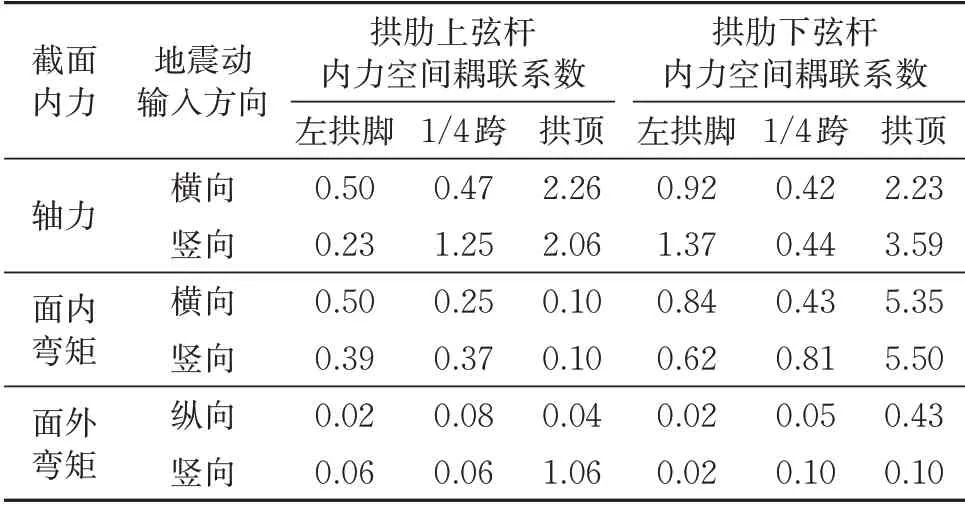
表2 Taft波激励下结构内力空间耦联系数

根据表1和表2的分析结果，可得到如下结论。

（1）对于由多片拱肋组成的钢桁拱桥，任何单方向地震动激励在拱肋弦杆内都将引起较大的轴力，拱肋弦杆轴力耦合显著，同时这种耦合也是必然的。原因有二：①纵向和竖向地震动激励下，拱肋将产生面内振动，而拱桥在面内为有推力结构，在拱肋弦杆内必产生轴力。②多片拱肋钢桁拱桥在横桥向可视为在拱脚处固定的多片曲线桁架结构，横向地震动激励下拱肋将发生侧倾变形，因框架效应将导致拱肋弦杆产生轴力［13-14］。

（2）横向和竖向地震动激励在拱顶区域弦杆内引起的轴力为纵向地震动激励下相应轴力的1.4～3.6 倍。这是因为横向和竖向地震动激励均能激发结构正对称振型，同时轴力又为正对称型结构内力，故导致拱顶处弦杆轴力显著增大，而纵向地震动激励只能激发反对称振型，故其在拱顶处引起的轴力较小。

（3）横向和竖向地震动激励在拱顶处下弦杆引起的面内弯矩为纵向地震动激励下相应弯矩的4.2～5.5 倍。除拱顶区域外，纵向和竖向地震动激励对拱肋弦杆引起的面外弯矩量值很小。

（4）普通的直线梁式桥水平向基本不存在耦合，但大跨复杂钢桁拱桥的地震响应空间耦联性显著，使结构地震响应变得更加复杂。

3 大跨上承式钢桁拱桥的地震动最不利激励方式及地震响应特征

由于地震动在时间和空间上的随机性，即地震动空间特性，因此对大跨度桥梁要确定结构产生的最大地震响应，仅考虑单维地震作用是不足的，还需要考虑多维地震动同时作用。对于地震动的选择，可以采用安评地震动或强震记录。对于大跨、复杂桥梁的抗震设计，通常由地震部门提供桥梁场址处的地震动安全评估报告，报告内提供了若干条超越概率不同的安评加速度时程记录。其中，加速度时程记录为水平方向的记录。对于地震动激励方式，《铁路工程抗震设计规范》［15］规定：竖向地震作用可按水平地震动的65%进行动力分析。而实际的地震动记录十分复杂，在不同的震级、震中距以及场地条件下记录的纵、横、竖向地震动强度及波形均不相同。综合考虑文献［15-16］的相关规定，本文假设沿桥梁纵向、横向及竖向输入的地震波均为同一条波，仅对其峰值进行调整，分析1维、2 维及3 维地震动激励对钢桁拱桥地震响应的影响。其中，1 维地震动激励方式为分别沿桥梁纵向（X向）、横向（Y向）输入地震波；2维地震动激励方式为沿X向，Z向或Y向，Z向同时输入（Z向指竖向）；3 维地震动激励方式为沿X向，Y向和Z向同时输入。具体地震动激励方式及组合见表3［17］。

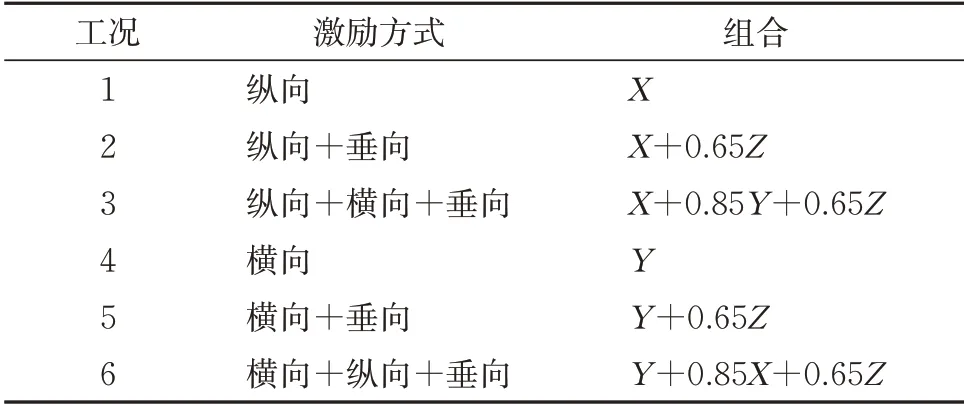
表3 地震动输入模式及组合

由于输入EL-centro 波和Taft 波时，2 条波的计算结果规律相似，所以只给出EL-centro 波的计算结果。输入EL-centro 波时不同地震动激励方式下拱肋上、下弦杆内力最大值包络图如图5—图10所示。为便于表述拱肋上、下弦杆最不利地震响应的影响规律，分2 组情况给出了拱肋上、下弦杆控制截面内力比的计算结果，见表4和表5。其中内力比定义为1 维和2 维激励时内力最大值与3 维激励时内力最大值的比值。

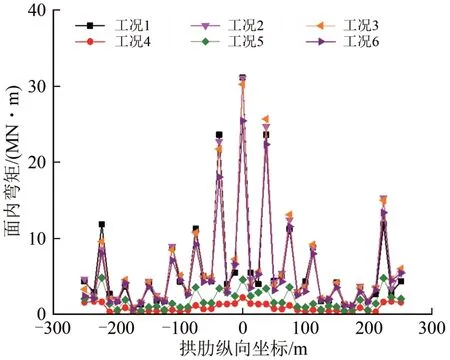
图5 拱肋上弦杆面内弯矩

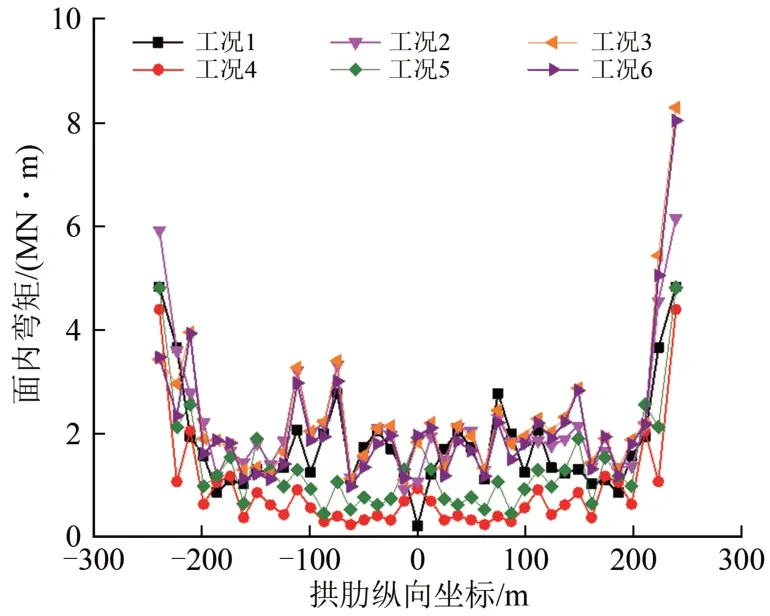
图6 拱肋下弦杆面内弯矩

图7 拱肋上弦杆面外弯矩

图8 拱肋下弦杆面外弯矩

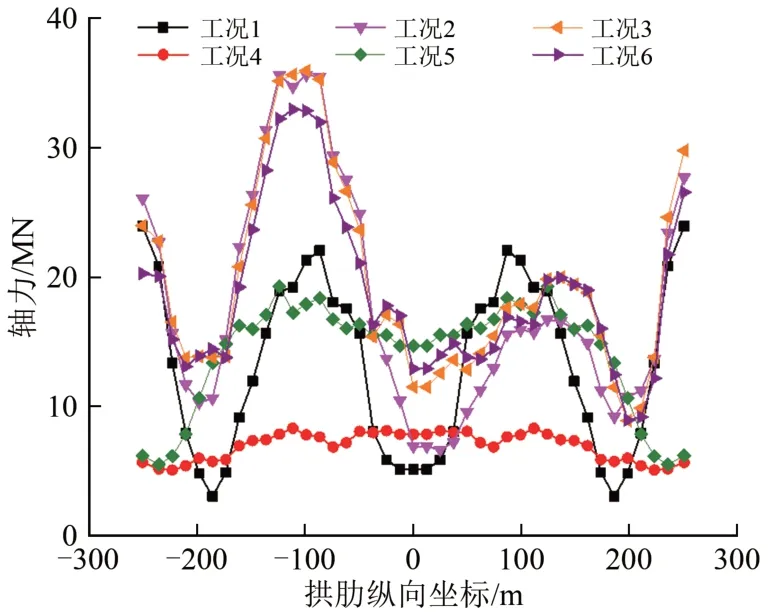
图9 拱肋上弦杆轴力

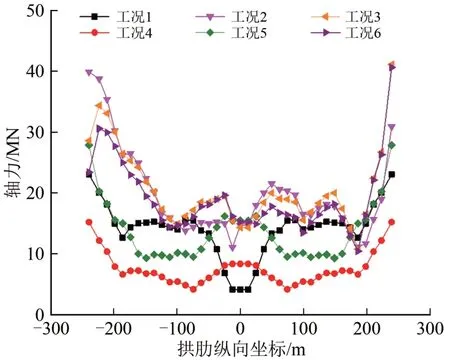
图10 拱肋下弦杆轴力

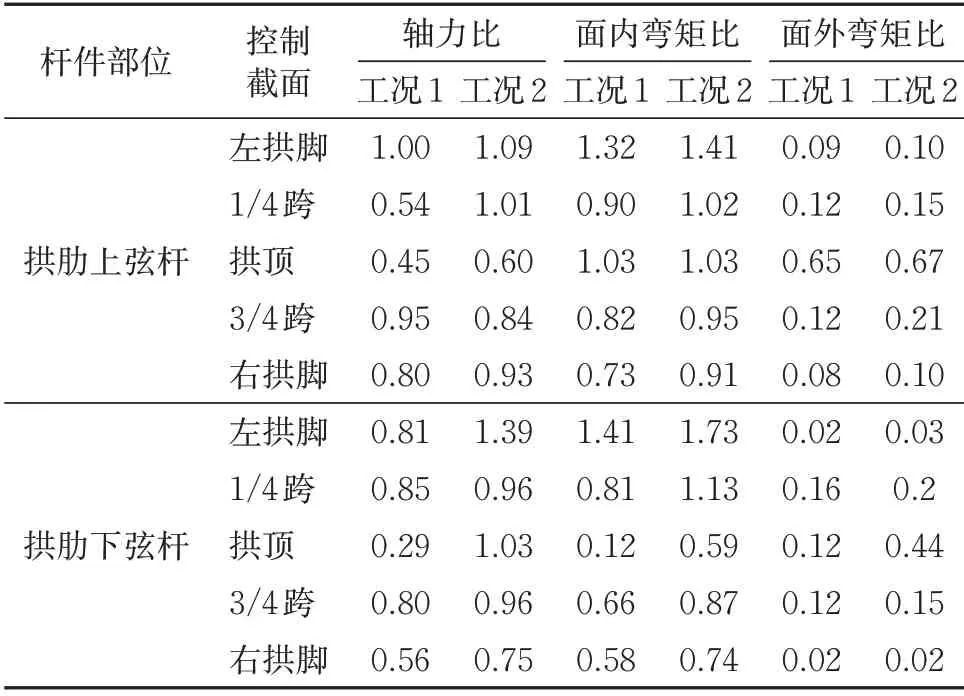
表4 拱肋控制截面内力比

由图5—图10及表4和表5可以看出如下结果。

（1）拱肋上弦杆在含有X向地震动激励下的面内弯矩与含有Y向地震动激励下的面外弯矩沿拱肋纵向均呈现明显的多峰值状分布特征，且各弯矩峰值点均与立柱的位置对应。拱肋上弦杆的面内、面外弯矩最大值均出现在拱顶处。而拱肋下弦杆的面内、面外弯矩最大值均出现在拱脚处，且该值明显大于拱肋其他部位的量值。

表5 拱肋控制截面内力比

（2）对拱肋下弦杆，因拱脚截面的轴力与弯矩均明显大于其他部位，故拱脚处为抗震薄弱部位。但对拱肋上弦杆，拱脚处、拱顶处及立柱与上弦杆相交部位的内力值均相对较大，故这些部位均可成为潜在的抗震薄弱部位。

（3）在多维地震动激励下，拱肋上、下弦杆的轴力最大绝对值分布规律明显不同。上弦杆轴力最值呈非对称简谐函数分布，但下弦杆轴力最值主要出现在拱脚处，向跨中方向急剧衰减。值得注意的是：在1维地震动激励下，拱肋弦杆的内力最大绝对值也是对称的。但在多维地震激励下，即使结构对称，拱肋弦杆对称位置的控制截面轴力最大绝对值并非呈现对称性，这一点与结构力学中的有关概念并非一致。因此采用时程反应分析法对钢桁拱桥进行多维地震动下地震响应分析时，应沿整个拱肋选取若干控制截面并逐一提取相应的内力进行组合验算。

（4）因结构空间耦合效应及各方向单维激励下拱肋内力响应最值不一定同步发生，导致并非地震动同时激励维数越多，主拱肋弦杆的截面内力就越大。多维地震动同步激励时，若各方向1维激励下拱肋内力响应同步同号，则多维激励下拱肋内力响应大于单维激励下拱肋内力响应。反之，若各方向1 维激励下拱肋内力响应异号，则多维激励下拱肋内力响应要小于1维激励下拱肋内力响应。总体上看，2 维及3 维激励的分析结果明显大于1 维激励，建议对复杂钢桁拱桥应同时进行2 维及3 维地震动激励，以确定其最不利响应。

关于上述第（3）条中拱肋弦杆内力分布不对称性解释如下。以输入EL-centro 波时±124 m 处拱肋上弦杆轴力响应为例，在X向和Z向1 维激励下前10 s轴力时程曲线（时间段已包含轴力响应峰值）如图11和图12所示。从图中可以看出：在X向和Z向激励下±124 m 处拱肋上弦杆轴力时程曲线分别呈反对称和正对称特征（即轴力性质不同），而在X向+Z向2维激励下弦杆轴力最值需根据对应的轴力时程曲线进行代数叠加，最终导致拱肋上弦杆轴力分布是不对称性的。

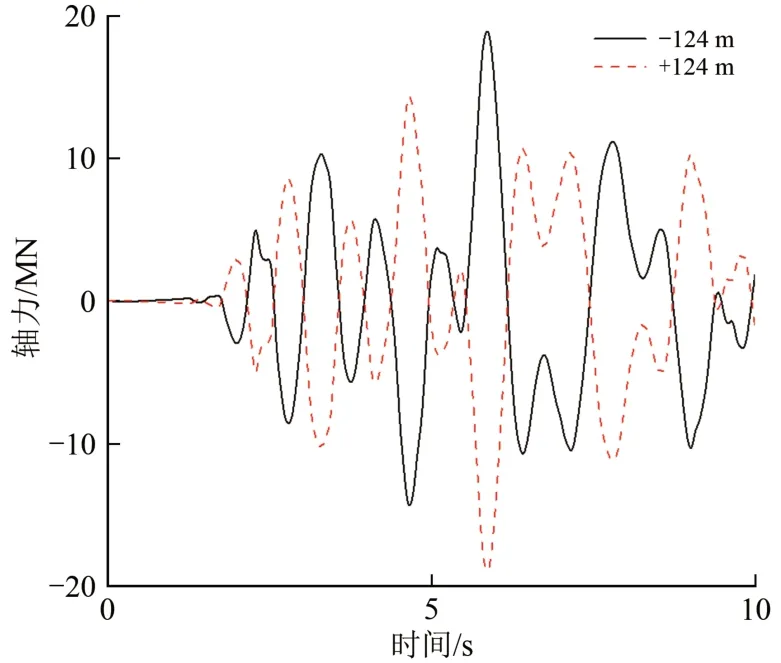
图11 X向激励下±124 m截面上弦杆轴力时程曲线

图12 Z向激励下±124 m截面上弦杆轴力时程曲线

关于上述第（4）条中拱肋弦杆内力最值与激励维数的关系解释如下。以输入EL-centro 波时拱肋上弦杆左、右拱脚轴力响应为例，在不同地震动激励方式下前10 s轴力时程曲线（时间段已包含轴力响应峰值）如图13和图14所示。从图13可以看出：在X向和Z向1 维激励下左拱脚上弦杆轴力响应峰值在同一时刻发生（6.90 s）但轴力性质不同，同时在该时刻Y向激励下上弦杆轴力响应和X向激励下的响应峰值也异号，使轴力存在相互抵消现象，因此左拱脚上弦杆轴力在3维激励下的响应并非最大。从图14可以看出：右拱脚上弦杆轴力在X向和Z向1 维激励下响应峰值在同一时刻发生（6.90 s）且轴力性质相同，而在该时刻Y向激励下上弦杆轴力响应与X向和Z向的峰值同号，导致轴力存在累积放大现象，因此右拱脚上弦杆轴力在3维激励下拱肋轴力响应最大。

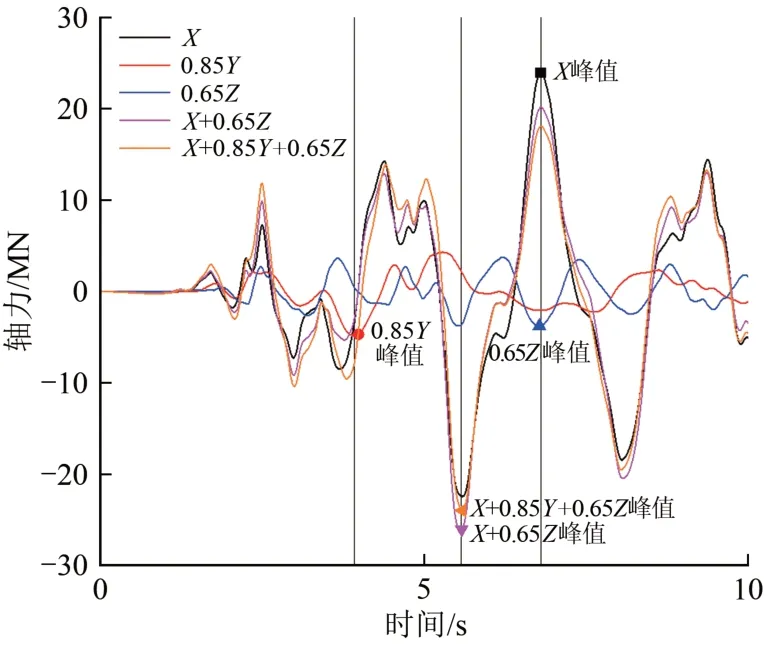
图13 左拱脚上弦杆轴力时程曲线

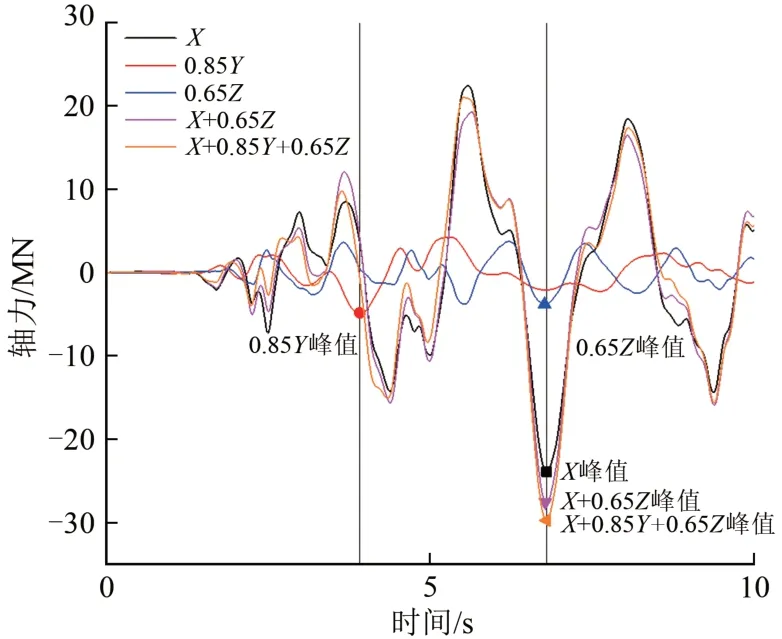
图14 右拱脚上弦杆轴力时程曲线

4 3维激励下拱肋弦杆内力控制分量

对于大跨上承式钢桁拱桥，因空间耦合效应显著，在多维激励下，弦杆内可产生6 个内力分量。其中，在弦杆截面产生正应力的内力分量主要有轴力、面内弯矩及面外弯矩。以弦杆截面的正应力分量为观察对象，以EL-centro 波作为输入地震动，采用工况6地震动激励方式，拱肋上、下弦杆各内力分量引起的正应力沿拱肋的分布情况如图15和图16所示。

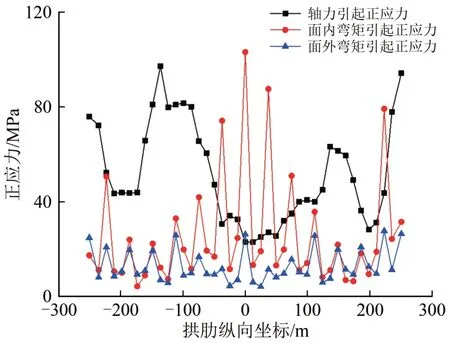
图15 拱肋上弦杆正应力分布

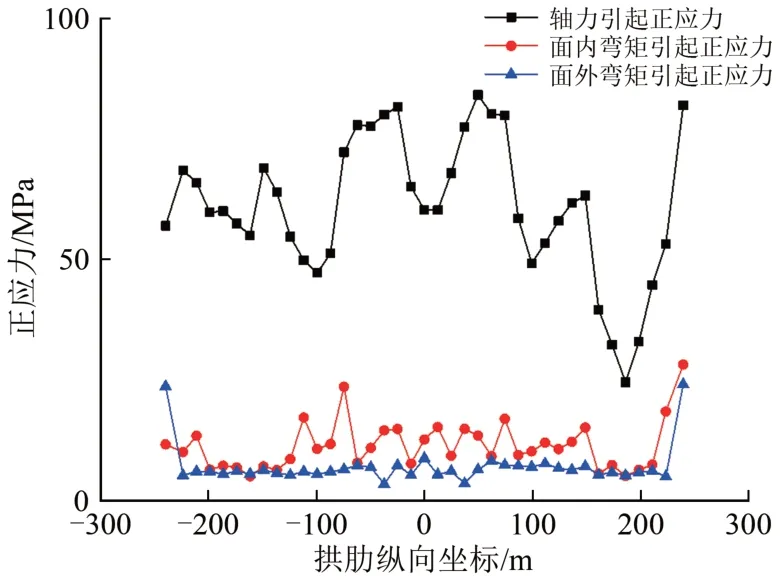
图16 拱肋下弦杆正应力分布

从图15和图16可以看出：对拱肋下弦杆，轴力引起的正应力显著大于面内弯矩和面外弯矩引起的正应力，即对拱肋下弦杆的正应力，轴力是起绝对控制作用的内力分量，这一点与桁架结构的受力特征相同。但从整个上弦杆的正应力量值大小及分布特征看，很难找到起绝对控制作用的内力分量，这一点与桁架结构的受力特征明显不同。在拱顶处、拱脚处和拱上立柱与拱肋连接处面内弯矩引起的正应力很大，尤其在拱顶处的面内弯矩引起正应力是轴力引起正应力的4倍以上，可见对拱肋上弦杆的正应力是由轴力、面内及面外弯矩共同控制的。探讨弦杆控制内力分量的意义在于可为杆件的截面尺寸定性调整提供参考：若杆件弯矩较大，则调整截面高度正应力变化显著；若杆件轴力较大，则可调整横截面面积，同时应关注其整体稳定性。