具有时滞状态导数反馈的高阶多智能体系统的一致性
2020-10-16晋守博
晋守博
近年来,多智能体系统的研究受到了广泛关注,该系统的优点在于能够较好地描述复杂的集体行为,如鱼群的游动、无人机群的控制以及计算机网络控制等.一致性是多智能体系统最重要的性质之一,为了使所有智能体随着时间变化能够达到一致,最关键的问题是构造控制策略.对多智能体系统的一致性的研究是目前的一个热点,针对如何实现系统的一致性,文献[1]和文献[2]分别从数值模拟和理论证明方面作了分析,多智能体系统是一种比较特殊的复杂系统,它的稳定性与系统的通讯时滞具有密切关系,近期许多学者都在研究时滞对系统的影响,针对低阶系统,文献[3-5]对该问题作了详细地讨论;针对高阶系统,文献[6-7]设计了一种仅依赖位置状态的控制策略,分析了系统的一致性问题.三阶多智能体系统可以表示如下:其中:i∈I,I= {1,2,…,N}表示智能体的数量集,函数xi(t),vi(t),zi(t) ∈R 代表位置、速度和加速度,函数ui(t) ∈R 是控制输入变量.
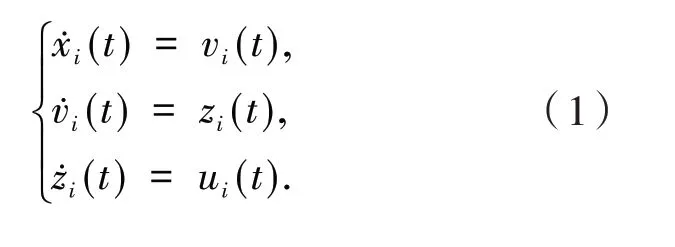
与一阶、二阶多智能体系统相比,系统(1)更加复杂,不仅能够描述智能体的位置和速度状态,而且能够描述加速度的变化情况[8-9].目前,对于高阶多智能体系统,大部分学者设计的控制策略里既包含位置状态,又包含速度和加速度的状态,然而,现实中智能体的速度和加速度很难测量,对于没有装备速度和加速度传感器的智能体,需要设计仅含有位置状态的控制协议,LIU 等讨论了只含有位置状态控制的二阶多智能体系统,我们将在如下控制策略下研究系统(1)的一致性,
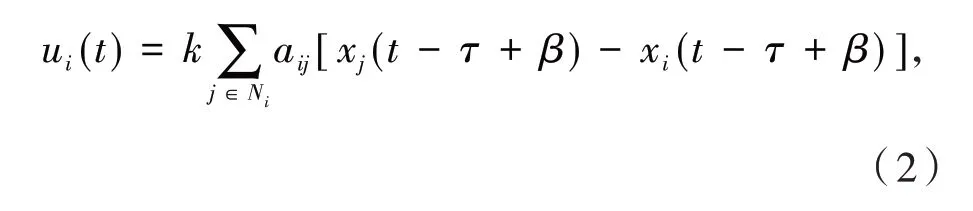
其中:常数β> 0,代表着反馈强度,aij为邻接矩阵的元素,能够反映出系统的网络拓扑结构,Ni表示与智能体i有关联的智能体集合,τ用来表示通讯时滞.
式(2)是一种包括反馈强度的控制协议,下文称协议(2),该协议最早在文献[10-11]中被提出,针对低阶情况,文章分析了反馈强度对一致性的影响,本文将把协议(2)用到更加复杂的三阶系统上.另外对于三阶多智能体系统,协议(2)仅含有位置状态,更具有现实意义,本文将结合文献[9-12]的方法,首先对xi(t-τ+β)做近似替换,计算公式为xi(t-
代入式(2),得到具有时滞状态导数反馈的一致性协议(3)
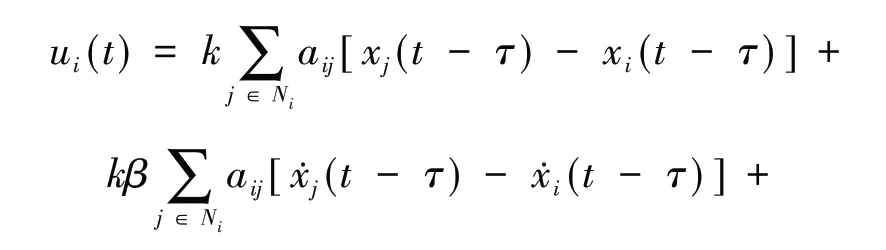

其中:β> 0 表示时滞状态导数的反馈强度,一般地,β越接近0,协议(2)和协议(3)的近似度越高,与文献[9]相比,协议(3)具有更强的实用性.
1 主要研究结果
定义1 如果对所有i,j∈I,系统(1)在任意初始条件下都满足0,则多智能体系统(1)称为渐近稳态一致,
本文将在无向拓扑结构下,研究系统(1)的渐近稳态一致性.
引理1[12]记L为系统的拉普拉斯矩阵,则当系统(1)的拓扑结构图无向且连通时,L必定有一个零特征值,特征向量为1N=(1,1,…,1)T,其他特征值实部都大于零.
引理2[9]如系统(1)在协议(3)下的渐近稳态一致性,则对任意i∈I下式成立.
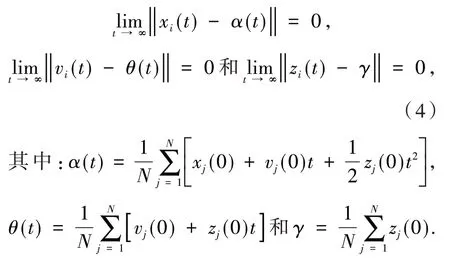
为了研究系统(1)在协议(3)下的一致性,记ξ(t) = (x1(t),v1(t),z1(t),…,xN(t),vN(t),zN(t))T,则式(3)可变为
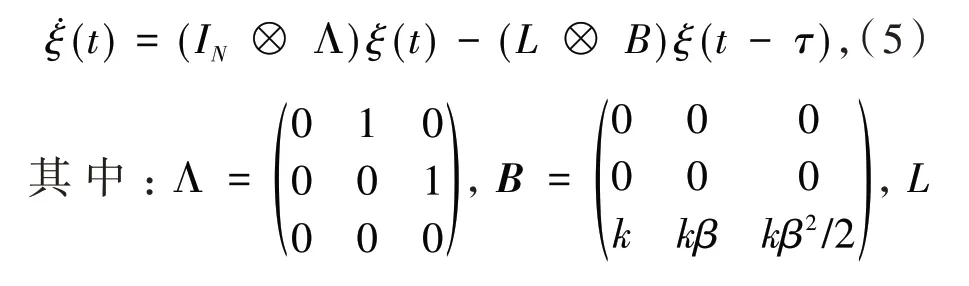
表示拉普拉斯矩阵,下面给出本文的主要结论.
定理1 对于多智能体系统(1),如果它的拓扑结构图是无向且连通的,则在协议(3)下,当且仅当
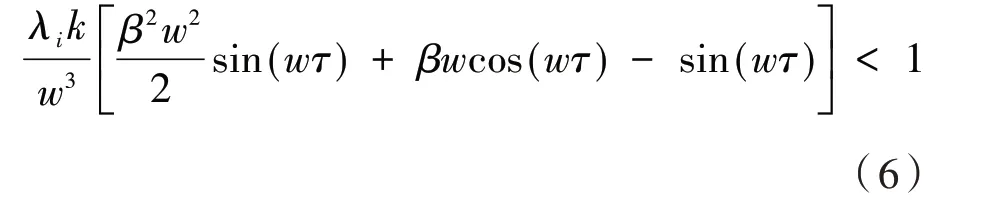
时,系统能够实现渐近稳态一致,这里的w为方程
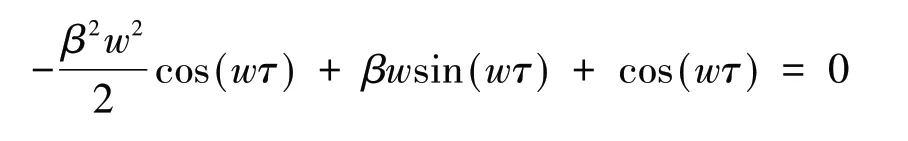
的根.
证明 利用引理 2,取E(t) =ξ(t) -式(5)经过计算后可得
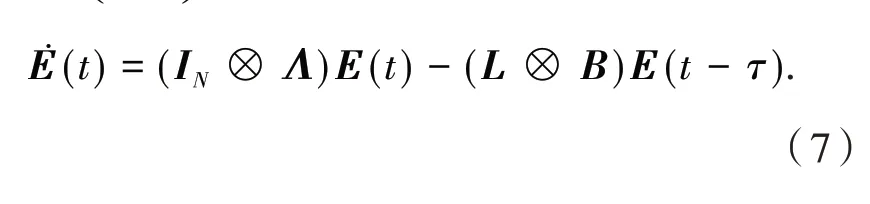
由引理1 可知,L的特征值可以记作λ1=0,0 <λ2<λ3< … <λN,而且必定可以找到一个正交矩阵W,满足
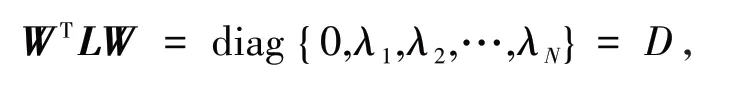
再利用引理1 中的特征向量是1N,则在 系 统(7)两边乘以WT⊗I3可得
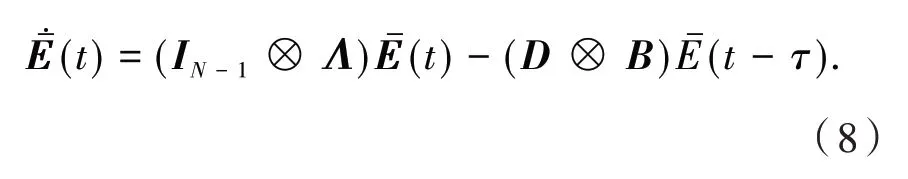
从上面分析可以看出,系统(7)的一致性与方程(8)的渐近稳定性等价,从而只要保证方程(8)的特征值全部在开的左半平面即可.
下面利用频域分析法证明方程(8)的特征值全部落在开的左半平面上.首先对方程(8)两边求拉普拉斯变换,可得
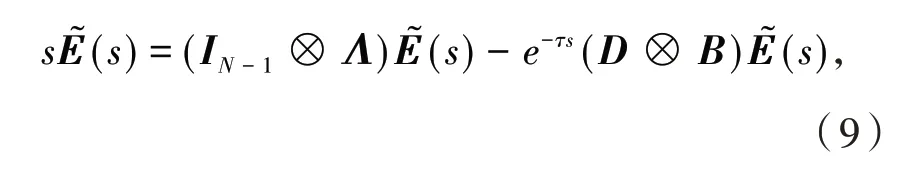
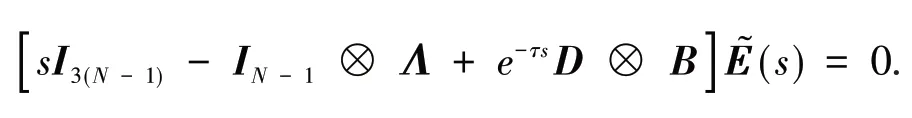
经过计算后可得
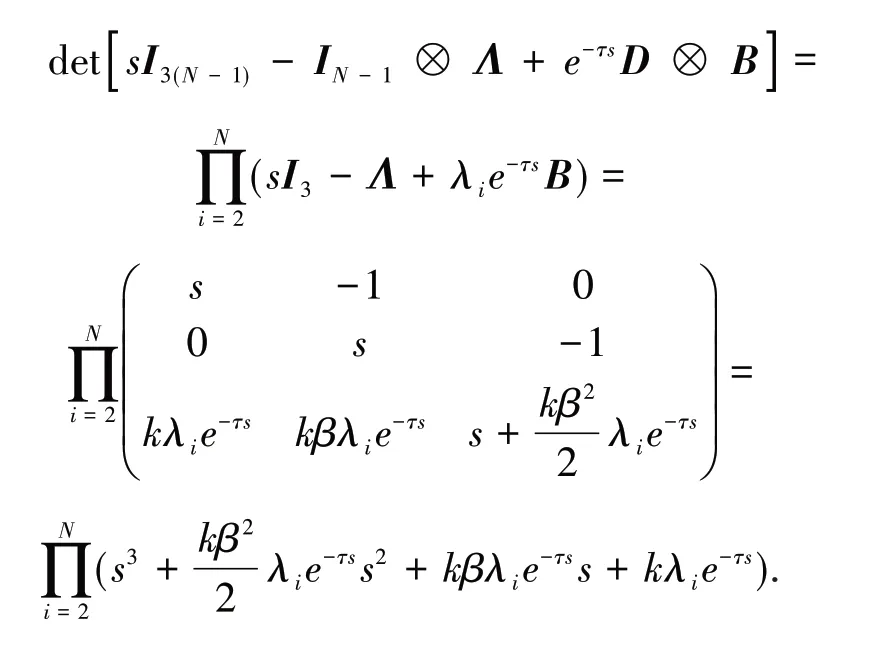
为了确保方程(8)的根在开的左半平面上,只要对任意i∈I/{1},方程

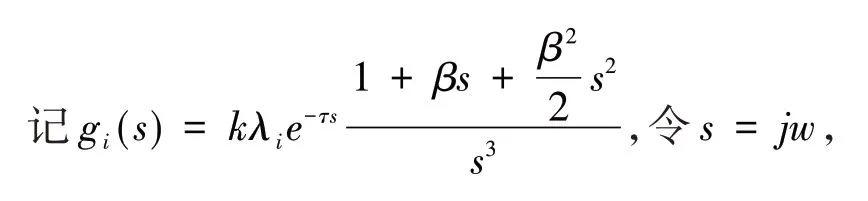
则
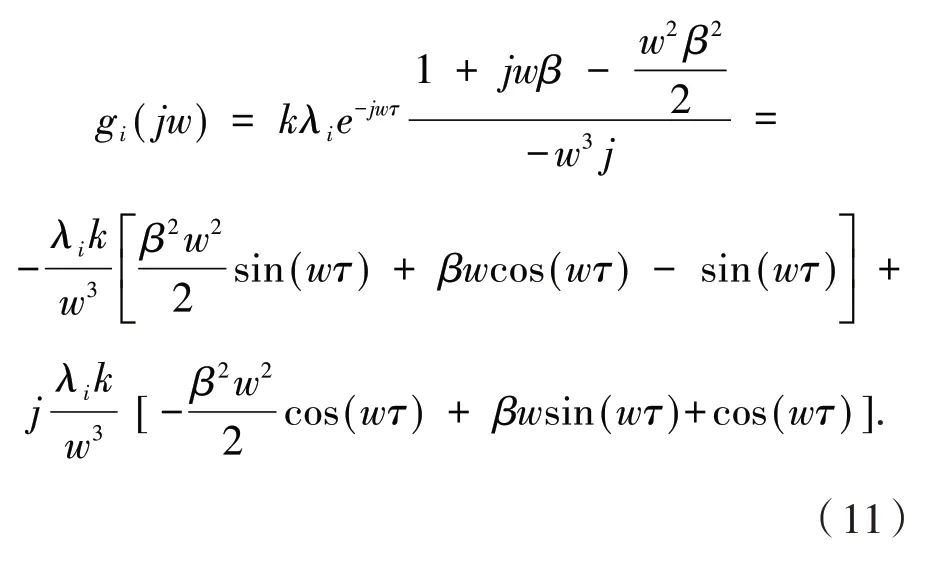
奈奎斯特稳定性判据是判定系统稳定性最常用的方法,此处将采用该方法分析方程(10)的稳定性,目前有很多学者都在采用这种方法证明稳定性问题,本文的核心思想也是该方法,关于该方法的更多应用可以参考文献[9],本文为了使得方程(10)的根全在开的左半平面,根据该稳定性判据,只要奈奎斯特曲线gi(jw) 不包围点(-1,j0) 即可. 另外,不包围点(-1,j0)的充要条件是
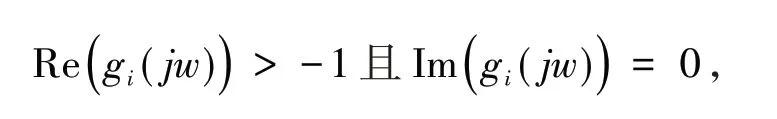
同时,由公式(11)可得
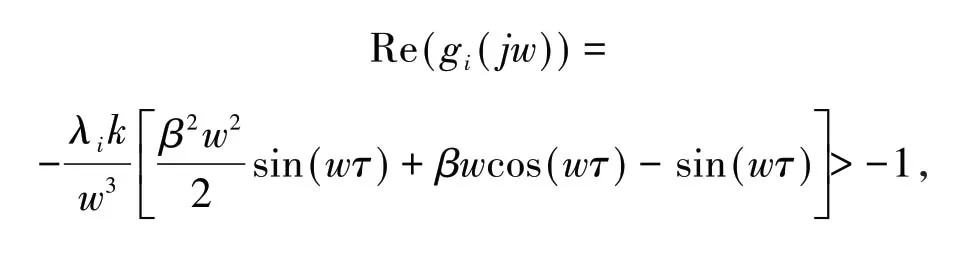
且

简单计算后可得
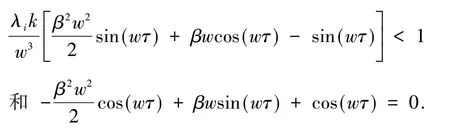
再利用λi的单调性,可得定理1 成立.
2 仿真实例
多智能体系统的拓扑结构见图1,系统的拉普拉斯矩阵可表示为经过计算,可以得到矩阵的四个特征值依次为λ1= 0,λ2= 2,λ3= 4,λ4= 4.
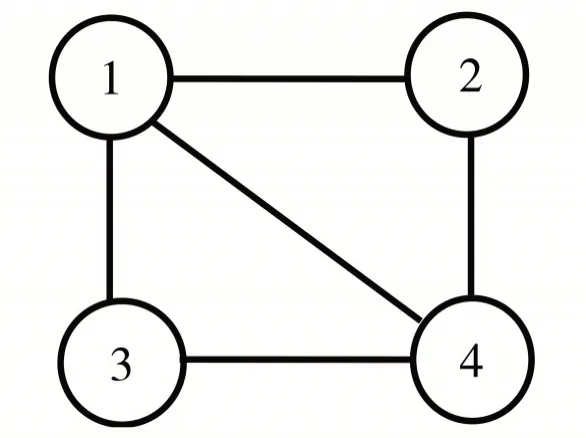
图1 多智能体系统的无向加权连通图
设参数k= 12,当β= 0.6,τ= 0.13 时,定理1 的条件可以满足;当β= 0.7,τ= 0.14时,定理1 的条件不能被满足,两种情况的仿真效果如图2 所示.

图2 系统(1)在不同反馈强度和时滞下的状态曲线
从图2 可以看出,当三阶多智能体系统引入时滞状态导数反馈协议后,只要通讯时滞和反馈强度满足一定的条件,即可实现渐近稳态一致性.
3 结语
研究表明,针对三阶多智能体系统,当输入状态仅与位置相关时,可以利用近似代换的方式,将输入状态转换为具有时滞状态导数反馈的多智能体系统,而该系统是一致的.另外,反馈强度越接近零,这种近似代换后的系统越能反映原系统的真实情况.
