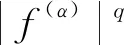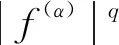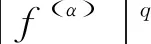分数积分下的关于m-凸函数的Hermite-Hadamard型不等式 *
2020-10-15叶小彩黄敏杰邱克娥
徐 冬,叶小彩,黄敏杰,邱克娥
(贵州师范学院数学与大数据学院,贵州 贵阳 550018)
0 引言
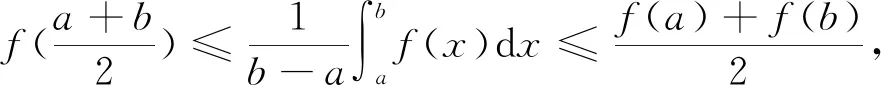
1 预备知识
记I为实数集R上的一个子集,I0为I的内部,Rα为分形空间上的实数集合,若aα,bα,cα∈Rα(0<α≤1),则在Rα中代数运算[5,6]满足:
(1)aα+bα∈Rα,aαbα∈Rα;

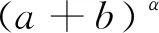
(4)aαbα=bαaα=(ab)α=(ba)α;
(5)aα(bαcα)=(aαbα)cα;
(6)aα(bα+cα)=aαbα+aαcα;
(7)aα+0α=0α+aα=aα,且aα1α=1αaα=aα.
定义1[5,6]设g:R→Rα,x→g(x)是一个不可微函数,如果对任意的ρ>0,总存在σ>0(其中ρ,σ∈R),使得当|x-x1|<σ时,有|g(x)-g(x1)|<ρα,则称不可微函数g(x)在x1处局部分数阶连续。如果g(x)在区间(c,d)上局部分数阶连续,则记为g(x)∈Cα(a,b).
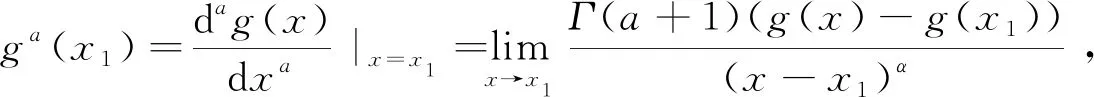
定义3[5,6]g(x)∈Cα(a,b),a=t0 定义4[7]设R+=[0,+∞],函数g:R+→Rα,对任意的x,y∈R+,t>0,有不等式g(tx+m(1-t))y≤tαg(x)+m(1-tα)g(y)成立,则称g为定义在R+上的广义m-凸函数(0 x(k-1) α; 引理4[4]设a (1) (2) 证明:对(1)式用幂均值不等式有 (3) (4) 由引理2可知 (5) (6) 同理可得: (7) (8) (9) 将(5)~(9)代入(4)式,并注意到 (10) 经计算简式可得(2)式,证毕。 (11) (12) 同理: (13) (14) (15) 将定理1的(4)、(10)以及(12)、(13)、(14)代入定理(9)式,经计算简式可得(11)式,证毕。 则下列带有局部函数积分的不等式成立: (16) 证明:对(3)式 (17) 再由引理2可得 所以 (18) 同理有 (19) (20) (21) 将(18)~(21)代入(17)中,通过计算化简可知(16)式成立,证毕。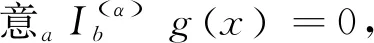
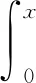
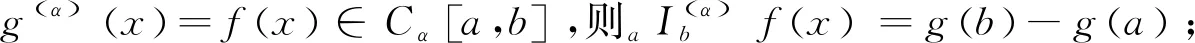
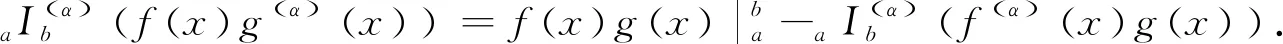
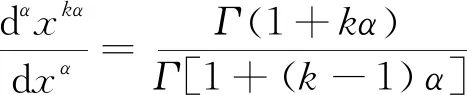
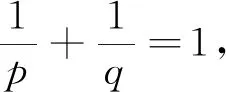
2 主要结果及其证明