例谈数学审题的“三要素”
2020-10-14◇闫瑞
◇ 闫 瑞
数学解题离不开审题,那么审题应该审什么?仁者见仁,智者见智.笔者认为审题主要有3个视角,即审条件、审结论、审方法,在此不妨称其为审题的三要素.本文以一道函数与导数综合问题的解答为例,从这三要素来谈谈审题.
例已知函数f(x)=sinx+alnx-1在点处的切线斜率为
(1)求a的值;
(2)求证:f(x)在(0,π)上存在唯一的极大值;
(3)直接写出函数f(x)在(0,2π)上的零点个数.
1 审条件
条件是题目所给的解题依据,是解题的入手点.题目所给的条件有的是直接的,有的是间接的,审清题目条件是解题的关键.
审本题中给出了曲线f(x)在点处的切线斜率,即点为切点,对于切点来说,其具有三重性质,即切点在曲线上、切点在切线上、在切点的导数值为切线的斜率.
解(1)求导得,解得a=1.
此问考查了导数几何意义的应用,此类问题求解中要注意曲线在某点的切线与过某点切线的区别.
2 审结论
结论是题目所求的或所证的内容,审结论要明确:要想得到这一结论,需要满足什么样的条件,接下来再去验证这些条件是否满足.
审本题第(2)问是求证f(x)在(0,π)上存在唯一的极大值.极值点,即导函数的变号零点,若结论成立,需满足f′(x)在区间(0,π)内单调,且f′(0)·f′(π)<0,其图象大致为图1或图2的情形.因此问题求证的过程,就是验证这些条件是否满足.
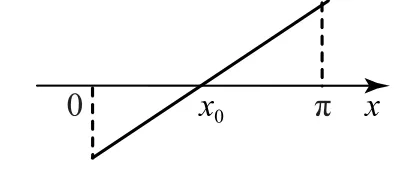
图1

图2
解(2)对函数f(x)=sinx+lnx-1求导得,易知当x∈(0,π)时,f″(x)<0恒成立,所以f′(x)在区间(0,π)内单调递减.又所以在区间(0,π)存在x=x0,使得f′(x0)=0.所以f(x)在区间(0,x0)内单调递增,在区间(x0,π)内单调递减,所以x=x0为f(x)在区间(0,π)内唯一的极大值点,f(x0)为唯一的极大值.
3 审方法
审方法是通过题目类型来确定简捷的求解方法,这就需要我们平时对题型进行归纳和总结.函数与导数的综合题,类型众多,但每种题型均有方法可循.
审本题第(3)问是判断函数的零点个数问题,常规方法往往需要借助函数零点存在定理,选择特殊点,并判断其函数值的正负.但此问要求直接写函数f(x)在(0,2π)上的零点个数,因此求解方法更加灵活,可将其转化为两个函数图象交点个数来处理.
解由f(x)=sinx+lnx-1=0,可得sinx=-lnx+1,设函数g(x)=sinx,h(x)=-lnx+1,在同一平面直角坐标系中画出函数g(x),h(x)的图象.其图形可能为图3或图4中的某种,再通过选取特殊值进行验证即可.
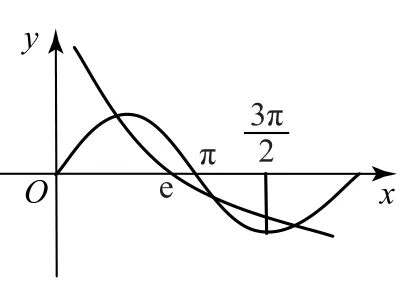
图4
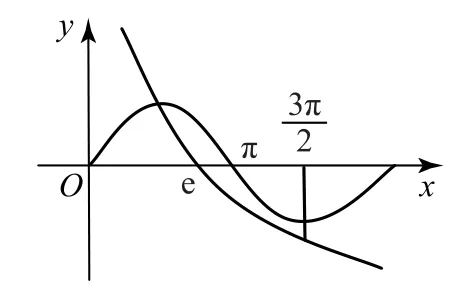
图3
由图易知在区间(0,π)内,函数g(x),h(x)有1个交点.在区间(π,2π)内,两函数图象交点的个数可借助的大小关系来判断.因所以函数g(x),h(x)的图象关系为图4所示情形,故两函数共有3个交点,函数f(x)有3个零点.
