高考大题增分专项之高考中的函数与导数

◇ 王学强

从近几年的高考试题来看，高考对函数与导数的考查已经从直接利用导数的正负讨论函数的单调区间(或利用函数单调性求函数的极值、最值问题)转变成利用求导的方法证明不等式，探求参数的取值范围，解决函数的零点、方程根等，甚至要求在某不等式成立的条件下，求某一参数或某两个参数构成的代数式的最值．

1 利用求导的方法证明函数不等式

突破策略1差函数法

证明函数不等式f(x)＞g(x)，可证f(x)－g(x)＞0，令h(x)＝f(x)－g(x)，或令h(x)为f(x)－g(x)表达式的某一部分，利用导数证明hmin(x)＞0．如果h(x)没有最小值，那么可以先利用导数确定出h(x)的单调性，再分析h(x)与0的关系．若h′(x)＞0，则h(x)在(a，b)上是增函数，若h(a)≥0，则当x∈(a，b)时，有h(x)＞0，即f(x)＞g(x)．

例1设函数f(x)＝lnx－x＋1．

(1)讨论f(x)的单调性；

(2)证明当x∈(1，＋∞)时

(3)设c＞1，证 明 当x∈(0，1)时，1＋(c－1)x＞cx．

(1)由题设可知，f(x)的定义域为(0，＋∞)，，令f′(x)＝0，解得x＝1．

当0＜x＜1时，f′(x)＞0，f(x)单调递增；当x＞1时，f′(x)＜0，f(x)单调递减．

(2)由(1)可知，函数f(x)在x＝1处取得最大值，最大值为f(1)＝0，所以当x≠1时，lnx＜x－1．故当x∈(1，＋∞)时，

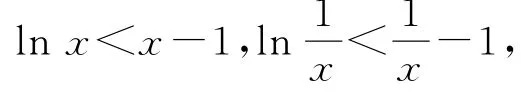
即

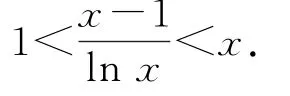
(3)由题设c＞1，设g(x)＝1＋(c－1)x－cx，则

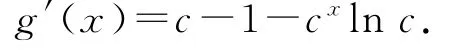
令g′(x)＝0，解得

当x＜x0时，g′(x)＞0，g(x)单调递增；当x＞x0时，g′(x)＜0，g(x)单调递减．由(2)知c，故0＜x0＜1，又g(0)＝g(1)＝0，故当0＜x＜1时，g(x)＞0．所以当x∈(0，1)时，1＋(c－1)x＞cx．

突破策略2求最值法

求最值法证明函数不等式依据表达式的结构有两种不同的证明方法:

1)要证f(x)≥h(x)，可令φ(x)＝f(x)－h(x)，只需证明φmin(x)≥0；

2)要证f(x)≥h(x)，可证fmin(x)≥hmax(x)；有时，要证f(x)＞h(x)，可引入g(x)，使得f(x)＞g(x)，然后再证明gmin(x)＞hmax(x)．

选用哪种方法要看用哪种方法构造出的函数的最值易求得．

例2已知函数

(1)求函数f(x)在区间[1，e2]上的最值；

(2)证明:对任意n∈N∗，不等式都成立(其中e为自然对数的底数)．

突破策略3设导函数零点法

若使用策略1或策略2解答中遇到方程f′(x)＝0不易求解，或无法解出导函数的零点x0时，可利用函数零点存在性定理设出导函数在区间(a，b)内的零点x0，再判断导函数在区间(a，x0)，(x0，b)的正负情况，从而判断出f(x)在x0处取得最值，求出最值，并通过对最值的处理消去x0使问题得到解决．

例3设函数f(x)＝e2x－alnx．

(1)讨论f(x)的导函数f′(x)零点的个数；

(2)证明:当a＞0时

(1)f(x)的定义域为(0，＋∞)，

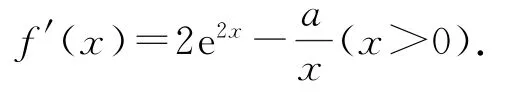
当a≤0时，f′(x)＞0恒成立，f′(x)没有零点；当a＞0时，因为y＝e2x在(0，＋∞)内单调递增，y＝内单调递增，所以f′(x)在(0，＋∞)内单调递增．又f′(a)＞0，假设存在b满足0＜b＜时，f′(b)＜0，故当a＞0时，f′(x)存在唯一零点．

(2)设f′(x)在(0，＋∞)的唯一零点为x0，当x∈(0，x0)时，f′(x)＜0；当x∈(x0，＋∞)时，f′(x)＞0．故f(x)在(0，x0)内单调递减，在(x0，＋∞)内单调递增，所以当x＝x0时，f(x)取得最小值，最 小 值 为f(x0)．由 于所以．故当a＞0时

2 有限制条件的求参数范围问题

突破策略1分离参数法

已知不等式在某一区间上恒成立，求参数的取值范围，一般先分离参数再转化为求函数在给定区间上的最值问题，即f(x)≥g(k)⇔fmin(x)≥g(k)，

f(x)≤g(k)⇔fmax(x)≤g(k)．

例4已知函数f(x)＝a(tanx＋1)－ex．

(1)若f(x)在x＝0处的切线经过点(2，3)，求a的值；

(2)由f(x)≥0，得令，则当时，g′(x)＞0；当时，g′(x)＜0．所以g(x)的最大值为故所求a的取值范围是

突破策略2分类讨论法

当不等式中的参数无法分离或含参不等式中左、右两边的函数具有某些不确定元素时，需应用分类讨论的方法来处理，使求参数的范围转换成讨论参数在哪些范围能使不等式成立．

例5已知函数f(x)＝(x＋1)lnx－a(x－1)．

(1)当a＝4时，求曲线y＝f(x)在(1，f(1))处的切线方程；

(2)当x∈(1，＋∞)时，f(x)＞0，求a的取值范围．(1)f(x)的定义域为(0，＋∞)．当a＝4时，．曲线y＝f(x)在(1，f(1))处的切线方程为2x＋y－2＝0．

(2)当x∈(1，＋∞)时，f(x)＞0等价于lnx－设，则

当a≤2，x∈(1，＋∞)时，x2＋2(1－a)x＋1≥x2－2x＋1＞0，故g′(x)＞0，g(x)在(1，＋∞)内单调递增，因此g(x)＞0．

当a＞2时，令g′(x)＝0，得x1＝a－1－和x1x2＝1，得x1＜1，故当x∈(1，x2)时，g′(x)＜0，g(x)在(1，x2)内单调递减，因此g(x)＜g(1)＝0．

综上，a的取值范围是(－∞，2]．

突破策略3求函数最值法

若等式两边变量不同的函数不等式恒成立，求不等式中的参数范围常用求函数最值法求解．

若对∀x1∈I1，∀x2∈I2，f(x1)＞g(x2)恒成立，则fmin(x)＞gmax(x)．

若对∀x1∈I1，∃x2∈I2，使得f(x1)＞g(x2)，则fmin(x)＞gmin(x)．

若对∀x1∈I1，∃x2∈I2，使得f(x1)＜g(x2)，则fmax(x)＜gmax(x)．

例6设

(1)讨论函数f(x)的单调性；

当x变化时，g′(x)，g(x)随x变化情况，如表1．

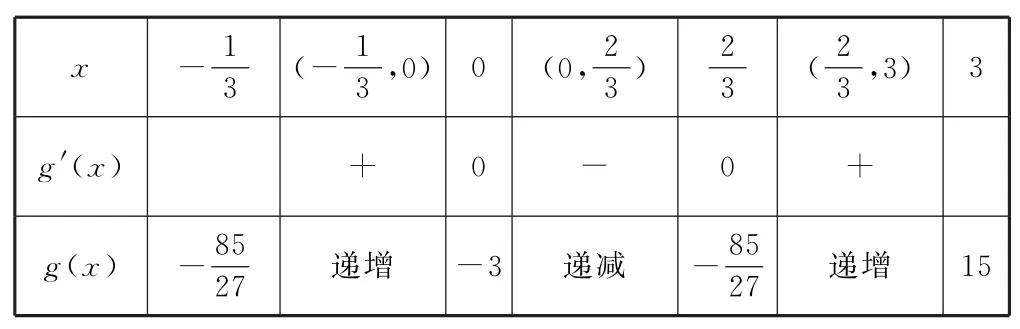
表1

由上表，可知

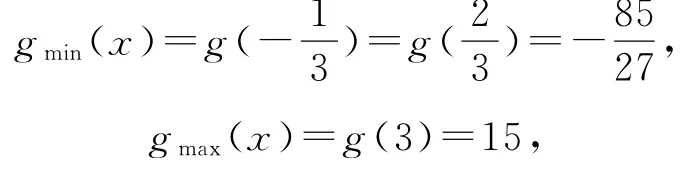
综上，a≥1．

3 判断、证明或讨论函数零点个数

突破策略1求导与数形结合法

研究函数零点或方程根的情况，可以通过导数研究函数的单调性、最大值、最小值、变化趋势等，并借助函数的大致图象判断函数零点或方程根的情况．其基本的思路为:1)构造函数并求其定义域；2)求导数得出单调区间和极值点；3)通过数形结合挖掘隐含条件，确定函数图象与x轴的交点情况进而求解．

例7函数f(x)＝(ax2＋x)ex，其中e是自然对数的底数，a∈R．

(1)当a＞0时，解不等式f(x)≤0；

(2)当a＝0时，求整 数t的所有值，使方程f(x)＝x＋2在[t，t＋1]上有解．(1)因为ex＞0，所以不等式f(x)≤0等价于ax2＋x≤0．又因为a＞0，所以不等式可化为，所以不等式f(x)≤0的解集为

(2)当a＝0时，方程f(x)＝x＋2即为xex＝x＋2．因为ex＞0，所以x＝0不是方程的解，所以原方程等价于

又h(1)＝e－3＜0，

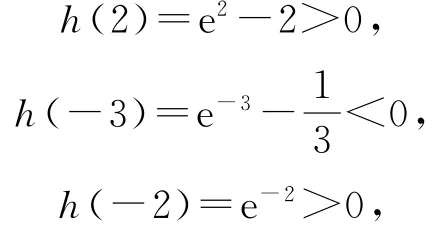
所以方程f(x)＝x＋2有且只有2个实数根且分别在区间[1，2]和[－3，－2]上，所以整数t的所有值为{－3，1}．

突破策略2分类讨论法

1)如果函数中没有参数，那么可以直接一阶求导得出函数的极值点判断极值点大于0和小于0的情况，进而判断函数零点的个数；

2)如果函数中含有参数，那么一阶导数的正负往往不好判断，这时要对参数进行分类讨论，判断导数的符号．如果分类后也不容易判断．那么需要对一阶导函数进行再次求导，在判断二阶导数的正负时，可能也需要分类．

例8已知函数(a∈R)．

(1)当a＝－1时，求函数f(x)的最小值；

(2)当a≤1时，讨论函数f(x)的零点个数．

(1)函数f(x)的定义域为{x|x＞0}，当a＝

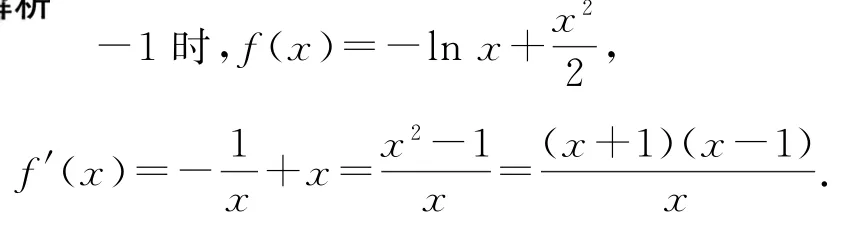
当0＜a＜1时，x∈(0，a)时，f′(x)＞0，f(x)为增函数；x∈(a，1)时，f′(x)＜0，f(x)为减函数；x∈(1，＋∞)时，f′(x)＞0，f(x)为增函数．所以f(x)在x＝a处取得极大值，f(x)在x＝1处取得极小值．

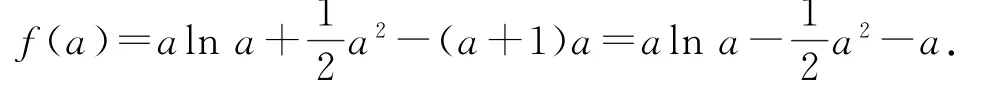
当0＜a＜1时，f(a)＜0，即当x∈(0，1)时，f(x)＜0．而f(x)在x∈(1，＋∞)时为增函数，且x→＋∞时，f(x)→＋∞，所以此时f(x)有1个零点．

当a＝1时在(0，＋∞)内恒成立，所以f(x)在(0，＋∞)内为增函数．且x→0(从右侧趋近于0)时，f(x)→－∞；x→＋∞时，f(x)→＋∞，所以f(x)有1个零点．

综上所述，当0≤a≤1或时，f(x)有1个零点；当时，f(x)无零点；当时，f(x)有2个零点．

4 专题总结

1)求解时，常常将不等式的恒成立问题转化为函数的最值问题；将证明不等式问题转化为函数的单调性与最值问题；将方程的求解问题转化为函数的零点问题、两个函数图象的交点问题等．

2)关于函数求导问题，在讨论函数单调性时，如果导函数值的符号不容易确定，那么一般是对导函数再次求导判断出导函数的单调性通过导函数的零点来确定导函数值的符号，从而判断出原函数的单调性；利用求导的方法可求出某一函数的最值，如果求出的最值仍然是含有变量的表达式，那么确定这一表达式的最值时仍然需要求导．

3)“恒成立”与“存在性”问题的求解是“互补”关系，即f(x)≥g(a)对于x∈D恒成立应求f(x)的最小值；若存在x∈D，使得f(x)≥g(a)成立应求f(x)的最大值．

4)所求问题如何转化成能利用导数解决的问题是关键．直接利用导数解决的问题一个是函数的单调性，一个是函数的极值或最值，所以应将具体问题通过等价转换(或构造函数)，使所求问题转化成与单调性或函数的极值、最值有关的问题．