城市污水处理过程出水氨氮优化控制
2020-10-12韩红桂杨士恒乔俊飞
韩红桂,杨士恒,张 璐,乔俊飞
(北京工业大学 信息学部;计算智能与智能系统北京市重点实验室,北京 100124)
出水氨氮浓度作为城市污水处理过程出水水质评价指标之一,其达标排放对确保城市污水处理过程稳定运行和保护水环境至关重要[1-2].然而,由于城市污水处理过程存在运行机理复杂、强非线性和随机干扰等特点,导致城市污水处理过程出水氨氮优化控制难以实现[3-4].如何设计一种有效的出水氨氮优化控制方法,提高出水氨氮处理效果,仍然是城市污水处理过程面临的难题[5-6].
为了实现出水氨氮浓度的优化控制,一些学者提出了基于城市污水处理过程机理模型的优化控制方法[7-8].Åmand等[9]设计了一种基于硝化反应机理的出水氨氮优化控制方法,该方法通过硝化反应过程物料平衡关系分析溶解氧浓度与硝化速率和出水氨氮浓度之间的关系,建立出水氨氮优化模型,利用非线性优化方法获取操作变量(氧气传递系数)的优化设定值,比恒定设定值控制方法减少了约4%的气体流量,降低了约14%的曝气能耗.Chen等[10]设计了一种基于活性污泥机理模型的优化控制方法,通过分析污水处理过程好氧阶段不同反应的耗氧量,建立曝气流量需求模型并结合氨氮及磷酸盐等水质约束条件优化该模型,优化调节溶解氧、水力停留时间和内回流等可控变量.虽然上述基于机理模型的出水氨氮优化控制方法能够改善城市污水处理运行效果,提高出水氨氮浓度去除率,然而,由于城市污水处理是一个时变的非线性操作过程,基于机理模型的出水水质氨氮性能指标模型参数难以根据动态的操作过程进行自适应调整,无法保证性能指标模型精度[11-14].为解决上述问题,Ozturk等[15]设计了一种基于混合整数非线性模型的出水氨氮优化控制方法,通过建立混合整数非线性性能指标模型来获取最优曝气剖面,得到溶解氧优化曲线,降低了出水氨氮浓度,减少了能耗.Antonio等[16]采用了一种基于非线性模型的优化曝气控制方法,通过非线性规划性能指标模型计算最优曝气策略,并将其应用于序批式反应器中,改善了出水水质,降低了能耗.Kim等[17]提出了一种实时反馈氨氮优化控制方法,根据溶解氧与氨氮之间的机理特征设计一种sigmod函数来表达两者之间的非线性关系,获得自适应变化的溶解氧浓度设定值,并采用PID控制器对溶解氧浓度进行跟踪控制,使溶解氧浓度变化范围更加理想,提高了氨氮处理效果.虽然上述基于数学模型的出水氨氮优化控制能够提高城市污水处理过程操作性能,但是依然难以满足出水氨氮优化控制的需求[18-19].
近年来,随着人工智能技术的快速发展,基于数据驱动的优化控制方法得到了学者的广泛关注[20-21].Zhang等[22]设计了一种污水处理过程泵送系统优化控制方法,通过神经网络建立泵速、流量等过程数据与泵耗之间的关系,获得了污水处理过程泵耗模型,并使用智能优化算法优化该模型获取泵速设定值,采用PI控制器对设定值进行跟踪控制,提高了系统表现并降低了能耗.Huang等[23]设计了一种混合神经网络控制的方法,利用模糊神经网络映射污水处理过程水质变量与曝气流量的关系,建立模糊控制规则库,从而实现对曝气流速率的控制,减少了约33%的能耗成本,降低了出水化学需氧量和出水氨氮的浓度.城市污水处理过程容易受到干扰的影响,设计有效的跟踪控制器实现对控制变量动态优化设定值的高精度跟踪控制仍然是一个挑战性难题[24-25].
为了解决上述难题,文中设计了一种数据驱动出水氨氮优化控制方法.通过机理分析建立曝气能耗与相关过程变量之间的非线性关系,构建了一种基于自适应核函数的污水处理过程曝气能耗模型,并使用梯度下降算法更新该模型,保证模型精度.同时,为了保证对溶解氧设定值的跟踪控制性能,文中设计了一种自适应模糊神经网络控制器(AFNNC)求取理想控制率.最后,将提出的出水氨氮优化控制策略应用于基准仿真平台BSM1,实现对出水氨氮浓度的优化控制.
1 城市污水处理过程运行特性分析
活性污泥法厌氧/好氧(A/O)工艺作为城市污水处理过程常用的处理方式如图1所示(SO,set(t)为溶解氧设定值,KLa为氧气传递系数,用于控制溶解氧的浓度),主要包括缺氧池、好氧池和二沉池3部分.在城市污水处理过程中,污水首先进入缺氧池,通过异养菌反硝化作用,将硝态氮转化为氮气,同时含氮有机物经过氨解作用将氨基转换为游离的氨氮,通过自养菌的硝化作用氨氮又转化为硝态氮,好氧池中污水一部分通过内回流将硝态氮送入缺氧池,进行反硝化过程,另一部分进入二沉池,经过沉淀、固液分离,将上清液排入自然水体.
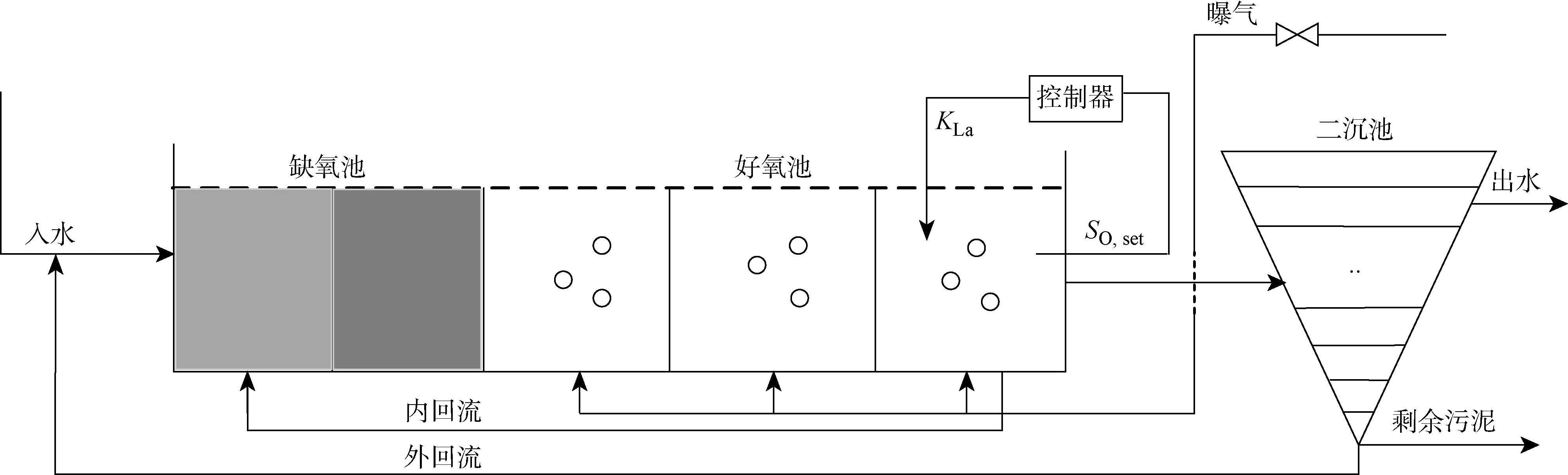
图1 A/O工艺过程Fig.1 Configuration of A/O
基于活性污泥1号模型(ASM1)中生化反应机理的描述[26],好氧池中氨氮浓度(下文中浓度均为质量浓度)变化过程可描述为
KaSNDXBH
(1)
式中:iXB为生物固态含氮量(质量分数);μH为异养菌最大比生长速率;SS为溶解性可快速生物降解有机物的质量浓度;KS为异养菌生长与底物利用饱和常数;SO为氧气浓度;KOH为异养菌氧呼吸饱和常数;XBH为活性异养菌的质量浓度;μA为自氧菌最大比生长速率;YA为自氧菌产率系数;SNH为氨氮浓度;KNH为自氧菌生长与底物利用饱和常数;KOA为自氧菌氧饱和常数;XBA为活性自氧菌的质量浓度;Ka为溶解性有机氮氨化速率;SND为溶解性可生物降解有机氮的质量浓度.
氨氮硝化反应过程受众多因素影响,在好氧阶段,氨氮的浓度主要受可生物降解底物和溶解氧浓度的影响,若好氧池中底物浓度充足,则溶解氧浓度为控制出水氨氮浓度的关键变量.一方面,如果溶解氧浓度过低,硝化反应速率和硝化菌生长速率将会受到影响,硝化过程不充分,导致系统的氨氮去除效率降低、出水氨氮浓度升高和反硝化的底物浓度不足,抑制反硝化作用;另一方面,若溶解氧浓度过高,不仅导致曝气能耗增加和运行成本提高,而且过多的溶解氧会随着内回流进入到缺氧区进而影响反硝化过程,最终降低脱氮效果.此外,污水处理过程中组分浓度变化剧烈频繁、干扰性强等因素也会影响氨氮硝化反应.因此,需要合理的优化控制氨氮去除过程,调节曝气池溶解氧浓度,适应不断变化的污水处理过程,达到最佳的控制效果.
2 基于自适应核函数的污水处理曝气能耗模型
在好氧阶段,氧气的消耗过程主要包含有机物的氧化、硝化作用和微生物的内源呼吸[27].自氧菌好氧生长过程中,氨氮作为硝化菌生长的能源用于合成新的细胞,所氧化的氨氮量与氧气消耗量成正比.异养菌利用氧气和可溶性底物进行好氧生长,需氧量为溶解性底物去除量减去微生物的增长量,自氧菌与异养菌的好氧生长过程为
(2)
(3)
式中:bA为自氧菌比衰减率;bH为异养菌比衰减率.
假设在曝气过程中溶解氧的浓度可以控制在恒定值,好氧池中溶解氧的浓度可表示为
SO,set(t)=
(4)
(5)
式中:Q为总进水流率(包括入水流率、硝酸盐回流和污泥循环流率);V为曝气池体积;SO,sat为溶解氧浓度饱和常数;r(t)为反应过程速率;SO,in为曝气池总进水溶解氧浓度;YH为异养菌产率系数.
基于上述分析,影响溶解氧浓度的过程变量主要为SNH、SS、XBH和XBA,而XBH和XBA的浓度又受到SNH、SS和SO的影响.因此,选择SNH、SO和SS为输入变量,EA为输出变量,建立以下模型:
EA(t)=y(SNH(t),SO(t),SS(t))
(6)
式中:EA(t)为曝气能耗;y(·)为关于自变量的非线性函数.
为了表征曝气能耗与相关过程变量之间的关系,通过自适应核函数的方法建立以下模型:
(7)
式中:y(t)和Wn(t)分别为系统t时刻模型的输出和对应权重;n(n=1,2,…,N)为核函数的个数;x(t)为t时刻模型的输入;cn(t)为t时刻第n个核函数的中心;σn(t)为t时刻第n个核函数的宽度.训练过程中,根据梯度下降法自适应调节模型的参数,使用误差平方和作为目标函数:
式中:E(t)为模型t时刻的误差平方和;e(t)为t时刻模型期望输出与实际输出之间的误差;yd(t)是模型t时刻的期望输出.模型的权值、中心和宽度表示如下:
式中:W(t+1)、c(t+1)、σ(t+1)分别为模型t+1时刻的权重、中心与宽度;η为学习率.t时刻各个参数的更新公式如下:
ΔW(t)=K(t)e(t)
(13)
Δc(t)=K(t)e(t)W(t)[x(t)-c(t)]/σ(t)2
(14)
Δσ(t)=K(t)e(t)W(t)[x(t)-c(t)]2/σ(t)3
(15)
式中:K(t)为模型包含的所有径向基核.
为了获得动态的溶解氧浓度,利用粒子群优化算法对建立的基于自适应核函数的曝气能耗模型进行优化,获得溶解氧浓度优化设定值,以保证城市污水处理过程的优化性能[28].
3 自适应模糊神经网络控制器
3.1 控制系统描述
溶解氧浓度控制系统特性表示如下:
s(t)=f(t)+g(t)u(t)+d
(16)
式中:s(t)为溶解氧浓度;f(t)和g(t)为未知函数;u(t)为控制输入;d为外界扰动.使用自组织模糊神经网络建立污水处理过程中的非线性动态模型,则最优控制率为
(17)
式中:qd(t)为期望输出;k为反馈增益系数,用于保证系统误差稳定性;控制器输入为a(t)和ov(t),a(t)为溶解氧浓度的实际值与期望值误差,ov(t)为误差变化量:
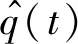
如图2所示,模糊神经网络分为4层,第1层为输入层:
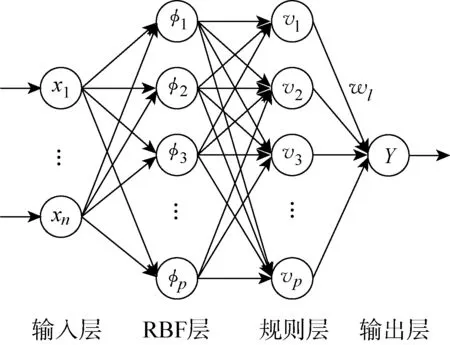
图2 模糊神经网络结构Fig.2 Configuration of fuzzy neural network
ui=λi
(18)
式中:λi为第i个输入变量,i=1,2,…,n.
第2层为径向基函数(RBF)层,该层对输入变量进行模糊化处理,选择高斯函数作为隶属函数,第j个神经元的输出为
(19)
式中:λ=[λ1λ2…λn]为第j个神经元的输入;zj=[z1jz2j…znj]为第j个神经元的中心;hj为第j个神经元的宽度;hj=[h1jh2j…hnj],i=1,2,…,n和j=1,2,…,p分别为输入变量的个数和RBF层神经元的个数.
第3层为规则层,神经元个数与RBF层相同(l=1,2,…,p),第l个神经元的输出为
(20)
第4层为输出层,功能为解模糊化,采用重心法进行归一化处理:
(21)
式中:Y为网络的输出;wl为规则层第l个神经元与输出层之间连接权重.
通过模糊化和去模糊化过程,AFNNC可以获得理想的控制率,实现对溶解氧浓度的控制,为了提高控制器的控制精度,需要对该控制器的参数进行更新.
3.2 参数更新
文中使用梯度下降算法对该控制器的中心、宽度、权值进行更新,定义控制器的优化目标函数如下:
(22)
rs(t)=g(t)[u*(t)-u(t)]
(23)
式中:rs(t)为系统控制误差;J(t)为性能函数.为使目标性能函数达到最小,各参数更新得
式中:zij、hij、wl和μ分别为控制器的中心、宽度、权值与学习率.
根据式(17)~(21),计算相应的控制率;根据式(22)~(26),对控制器参数进行更新.将上述控制器用于污水处理过程,实现对溶解氧浓度设定值跟踪控制.
4 实验结果与分析
文中采用BSM1中3种天气(晴天、雨天、暴雨)下的7天仿真数据进行实验,采样周期为15 min.通过对曝气能耗模型实时优化:优化周期为7 d,优化频率为12 h.为进一步分析所提出的优化控制方法的有效性,将该优化控制方法与不同天气下开环控制方法以及PID恒定设定值控制方法进行比较.此外,为了验证文中所提出的AFNNC控制器具有更好的控制性能,将其与PID控制器和BP网络控制器进行对比.
晴朗天气条件下的控制效果如图3所示,可得通过对曝气能耗模型进行优化,溶解氧浓度设定值随着时间不断变化,并且控制器能够较好的跟踪控制溶解氧的浓度.晴朗天气下溶解氧浓度的跟踪控制误差如图4所示,即使溶解氧浓度设定值在不断变化,控制器依然能够获得较好的控制效果,维持较小的控制误差.
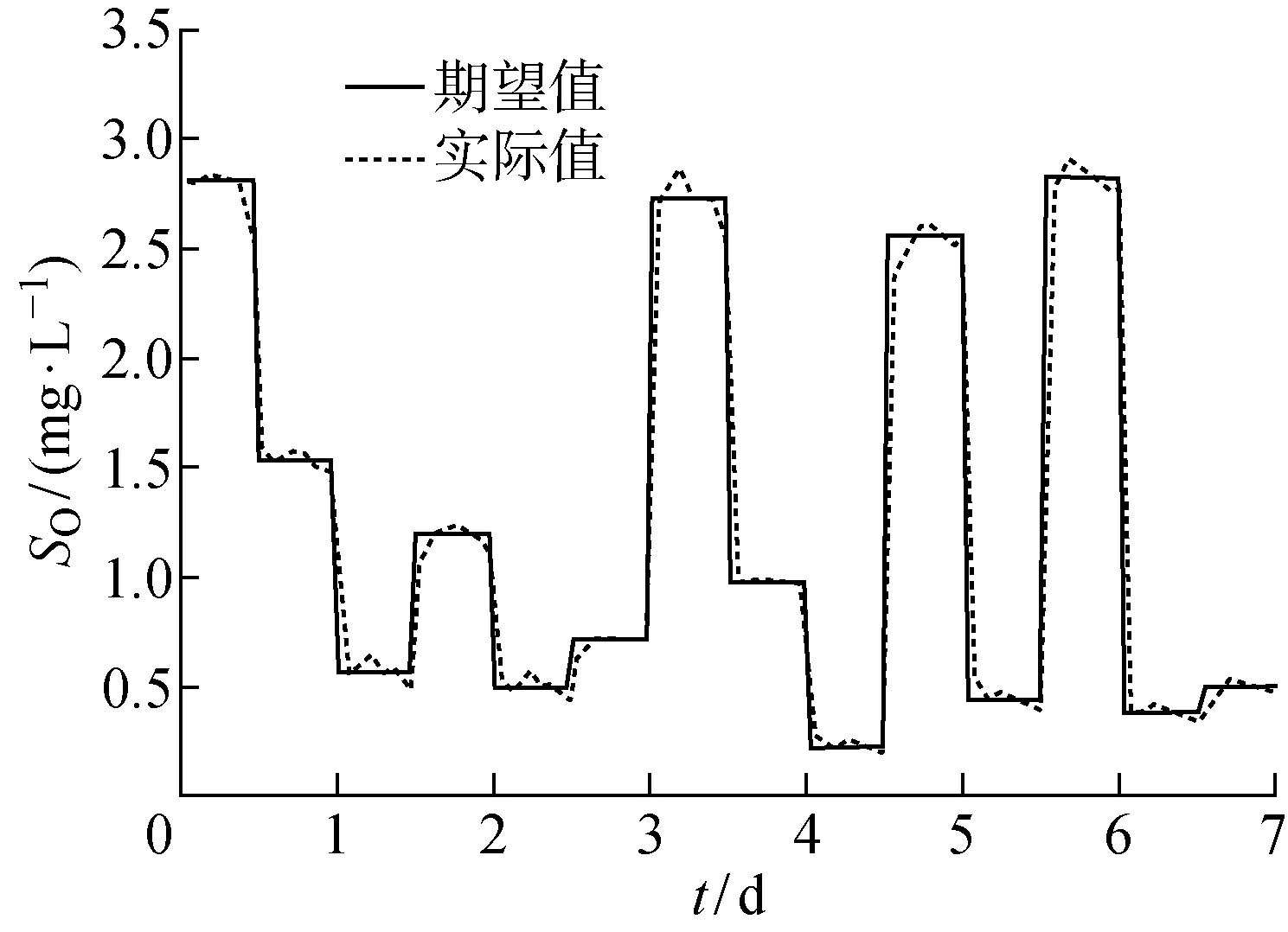
图3 晴天溶解氧跟踪控制Fig.3 Tracking control of oxygen on sunny days
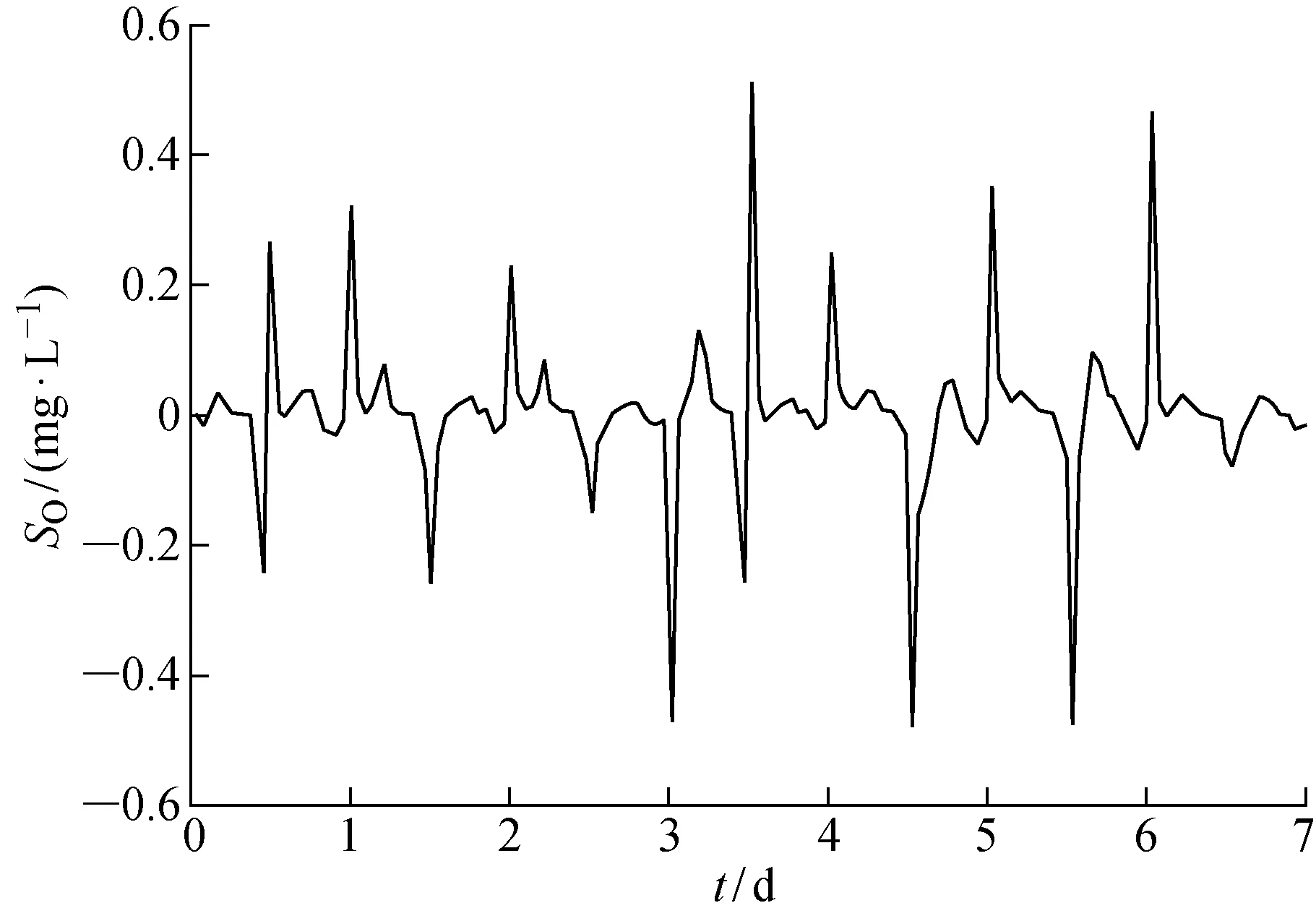
Fig.4 晴天溶解氧跟踪误差Fig.4 Tracking errors of oxygen on sunny days
雨天天气下溶解氧浓度的变化曲线,雨天天气下跟踪控制误差曲线,暴雨天气下溶解氧浓度的变化曲线和暴雨天气下跟踪控制误差曲线分别如图5~8所示,雨天天气和暴雨天气条件下伴随着水质和流量的不断波动.从图5和7中可知,即使在入水水质与入水流量波动的情况下,该曝气优化模型依然能够优化获得合适的溶解氧设定值,并且控制器能够对设定值进行稳定跟踪控制.从图6和8中可知,尽管系统存在着外界扰动,控制器依然能够保证较高稳定性与控制精度.
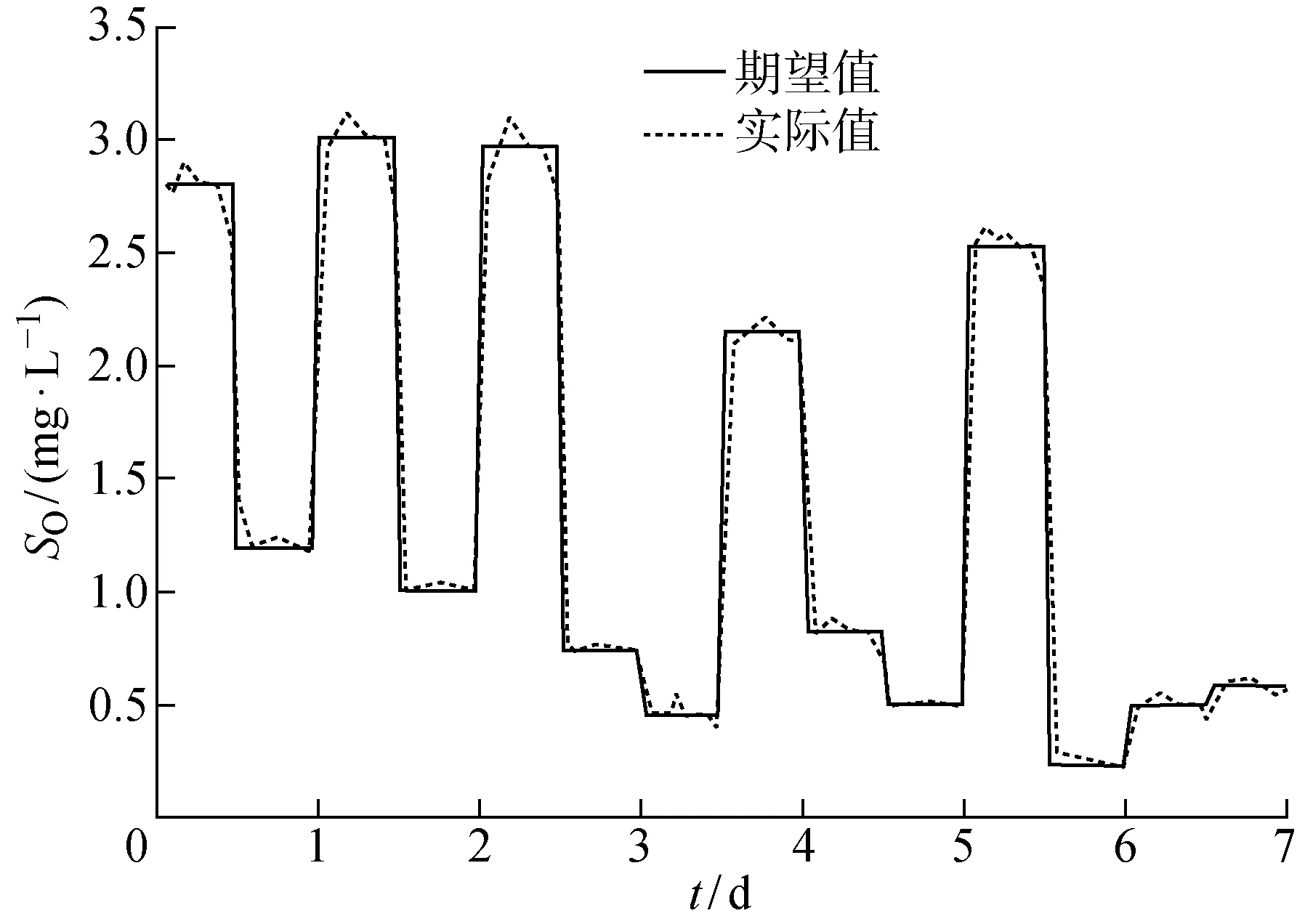
图5 雨天溶解氧跟踪控制Fig.5 Tracking control of oxygen on rainy days
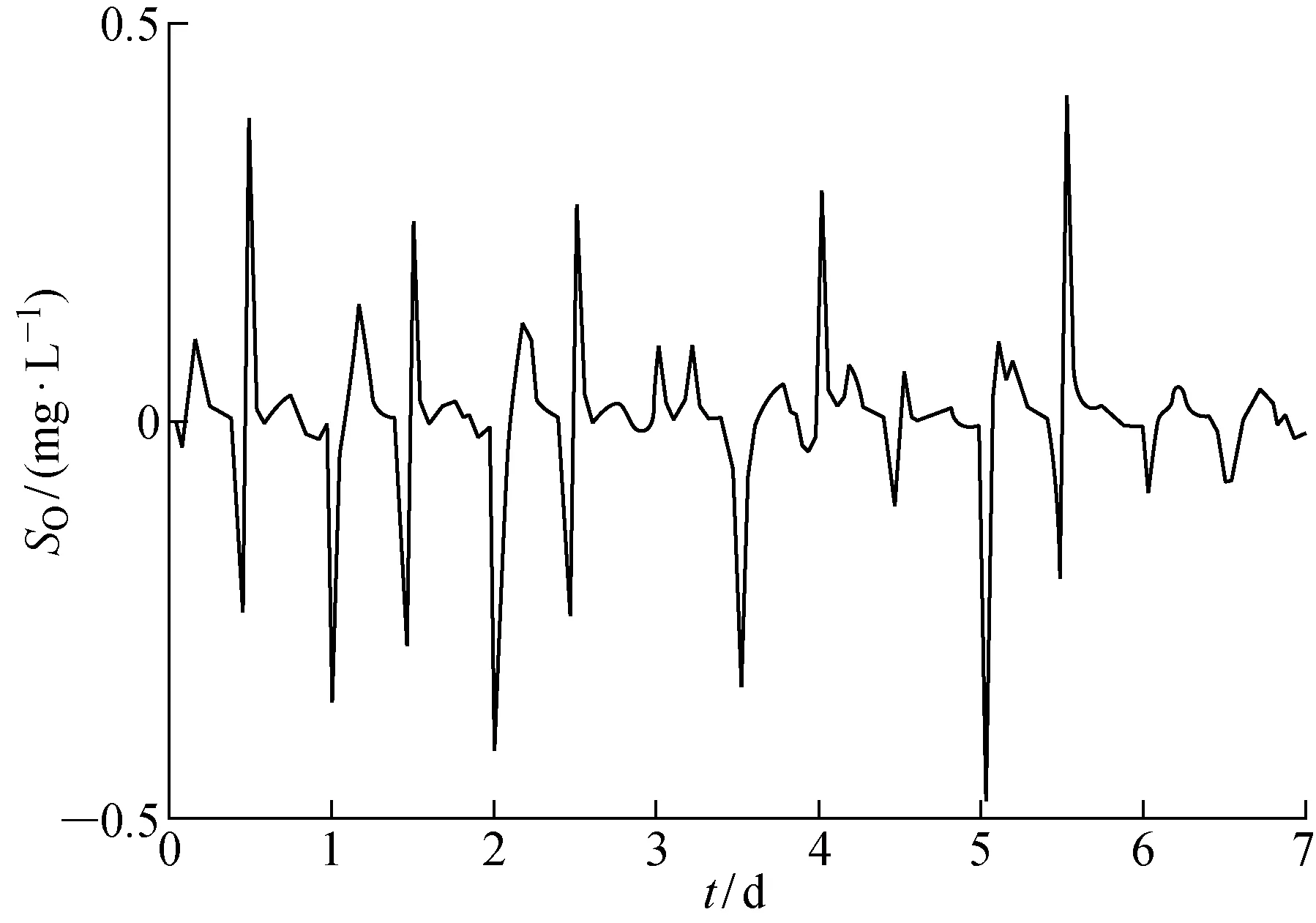
图6 雨天溶解氧跟踪误差Fig.6 Tracking error of oxygen on rainy days
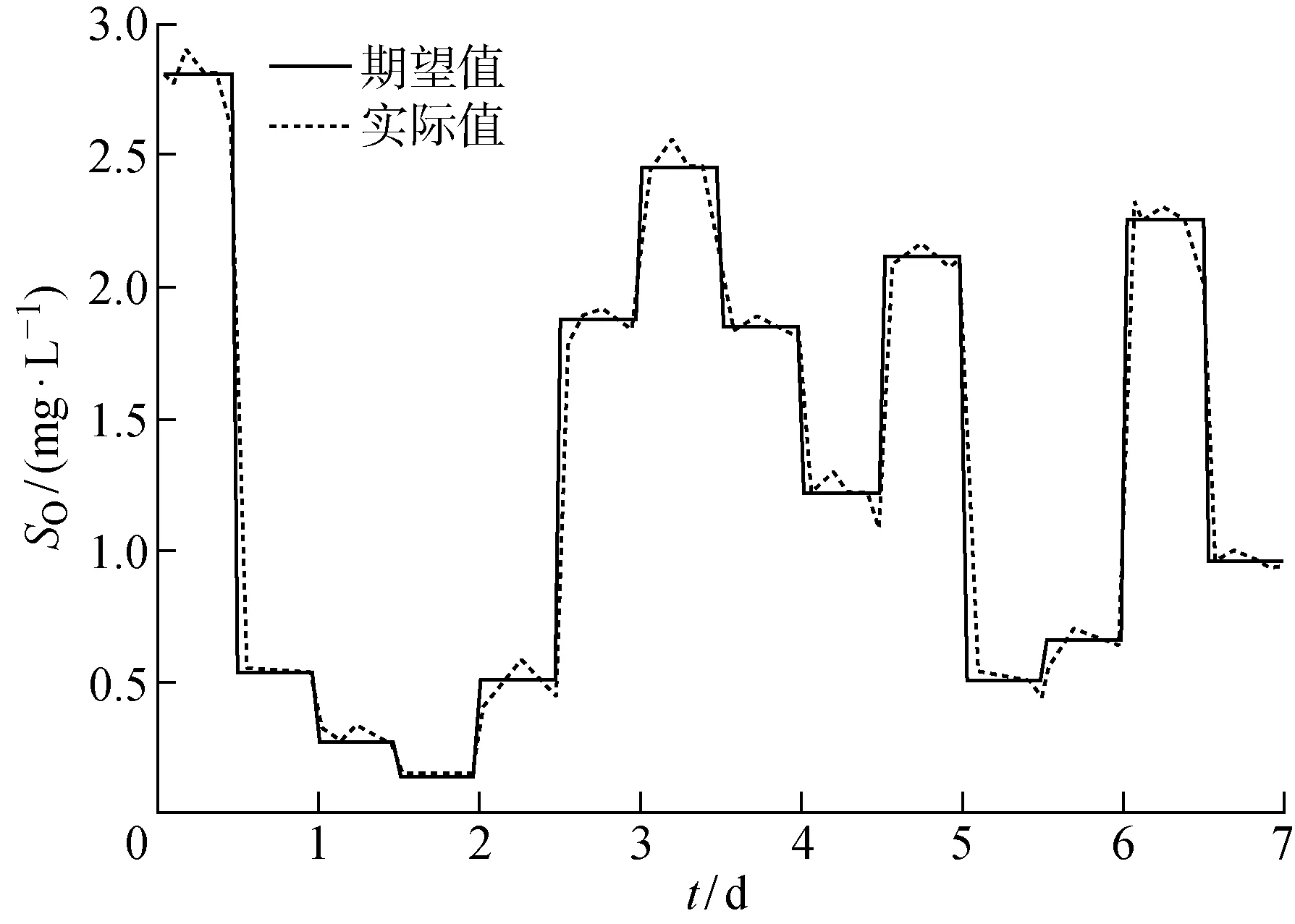
Fig.7 暴雨天溶解氧跟踪控制Fig.7 Tracking control of oxygen in storm day
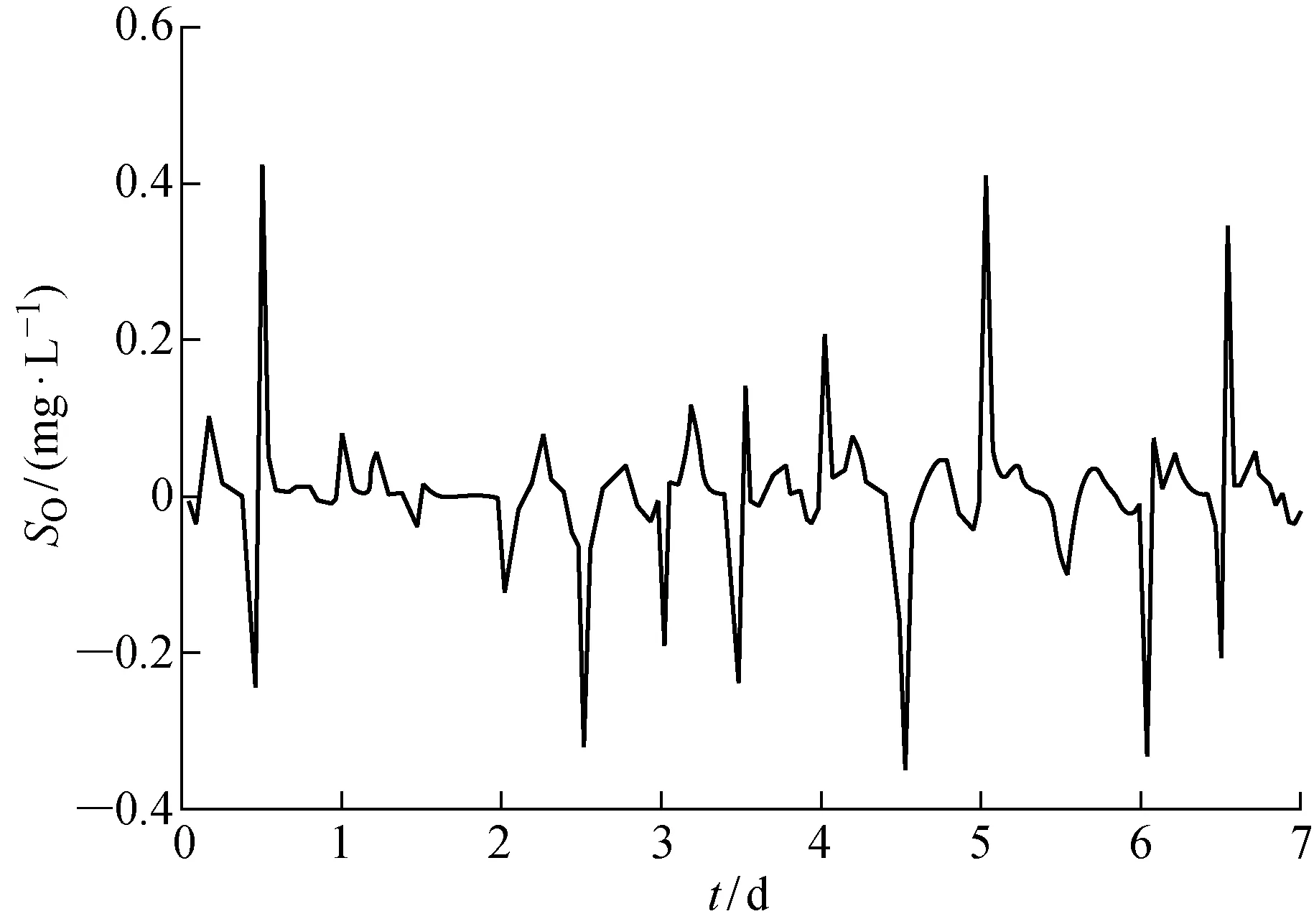
Fig.8 暴雨天溶解氧跟踪误差Fig.8 Tracking errors of oxygen on stormy days
3种天气下开环控制、PID恒定设定值控制和曝气过程优化控制3种方法比较结果如表1所示.从表中可见,在3种不同天气条件下,曝气能耗(AE)分别为 3 476 kW/h、3 425 kW/h和 3 443 kW/h,平均出水氨氮(SNH,avg)浓度分别为1.89 mg/L、1.95 mg/L和1.97 mg/L.与默认溶解氧设定值为2 mg/L的PID控制方法相比,减少了曝气能耗,降低了出水氨氮浓度.和开环条件下恒定KLa设定值控制相比,曝气能耗相对较高,但开环条件下出水氨氮浓度显著增高,导致出水水质恶化,相比之下,曝气优化控制方法出水氨氮浓度更低,效果更好.
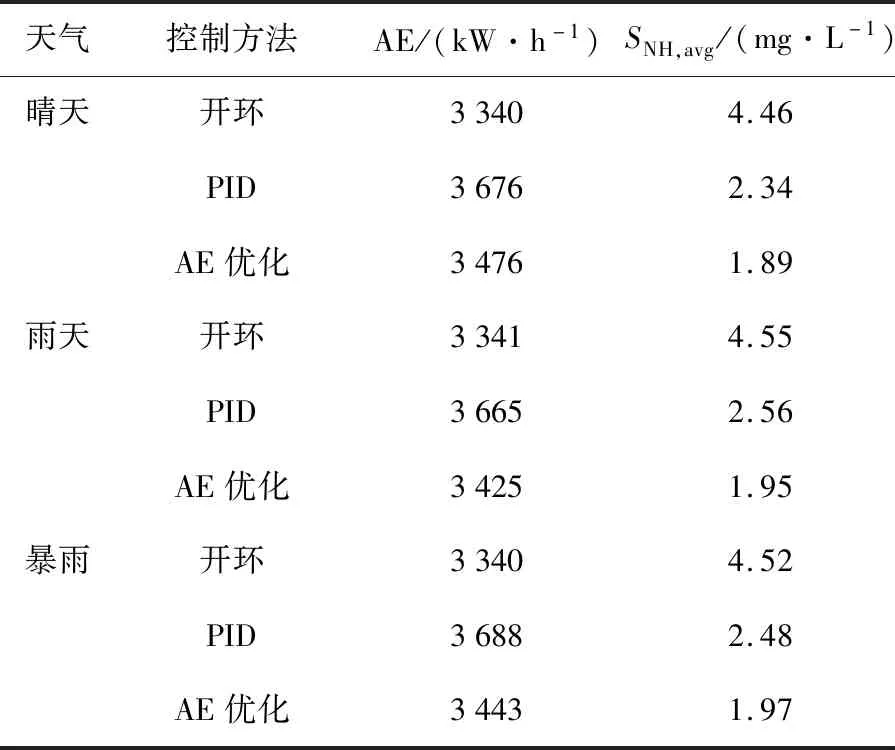
表1 不同控制方法比较Tab.1 Performance comparison of different control methods
为进一步验证文中提出的控制器的控制性能,将AFNNC控制器与其他控制器进行比较.3种天气下AFNNC控制器与其他两种控制器的比较结果如表2所示,在晴朗天气下,AFNNC控制器的绝对误差积分(IAE)和平方误差积分(ISE)分别为0.45和5.26×10-3;雨天条件下,AFNNC控制器的IAE和ISE分别为0.47和5.28×10-3;暴雨天气下,AFNNC控制器的IAE和ISE分别为0.43和5.16×10-3.结果显示,相比于其它两种控制方法,PID控制和BP算法控制,在不同天气条件下,无论是ISE还是IAE,AFNNC都具有更好的控制效果,显示了该控制器具有较强的稳定性与控制精度.
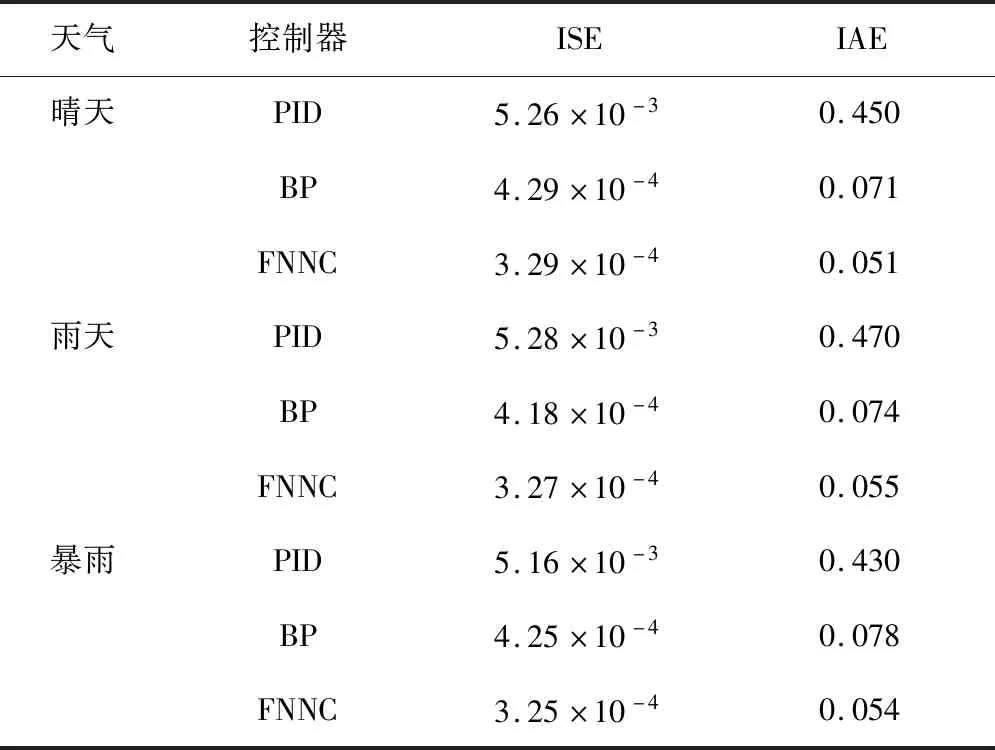
表2 不同控制器性能比较Tab.2 Performance comparison of different controllers
5 结语
针对城市污水处理过程出水氨氮难以控制的问题,文中设计了一种出水氨氮优化控制方法.该方法首先根据机理分析选择合适的相关变量,然后利用自适应核函数建立曝气模型,使用粒子群算法获取各个优化周期的溶解氧设定值并采用自适应模糊神经网络控制器保证跟踪控制性能.应用于BSM1的实验结果显示,该曝气模型能够充分反映污水处理过程中相关变量与能耗之间的特征,通过优化算法可以获取合适的溶解氧浓度设定值.与开环、恒定溶解氧浓度设定值两种方法相比,获得了更加优良的表现.此外,与传统的PID控制和BP算法控制对比,文中提出的自适应模糊神经网络控制器表现出了更高的控制精度与控制性能.
