欠驱动水面船舶的自适应神经网络-滑模路径跟随控制
2020-10-12贺宏伟邹早建曾智华
贺宏伟,邹早建,b,曾智华
(上海交通大学 a.船舶海洋与建筑工程学院;b.海洋工程国家重点实验室,上海200240)
船舶的路径跟随(Path Following)是要使船舶能够在一定的精度范围内有效地跟随预设的航线.与轨迹跟踪(Trajectory Tracking)问题不同的是,路径跟随只有空间的限制而没有时间的限制,因此可将其单纯地转化为对船舶横向偏差的控制问题.路径跟随控制的一大挑战是解决船舶的欠驱动问题,即要求通过采用某种制导方法,将船舶前进、横移、转艏3个自由度的运动控制简化为对航向(或航向和速度)的可控目标.在此领域内,使用最为广泛的是视线(Line-of-Sight,LOS)方法.LOS方法将对路径的跟随转化为对预设路径上一个点的跟踪,进而生成参考航向的时历曲线,船舶只要跟随参考航向便可有效地保持航迹[1-3].传统的LOS只能较好地处理无外界扰动时的路径跟随问题,甚至在无外界扰动的情况下,受漂角的影响,横向偏差也可能无法完全收敛至0.为了克服传统LOS的不足,衍生出了积分LOS(Integral Line-of-Sight,ILOS),其积分作用对只能依靠航向信息操舵的欠驱动船舶十分有效,使得这类船舶在海流或者慢漂波浪力的影响下能够有效地跟踪直线航路.Lekkas等[4]在LOS中引入积分环节,并设计自适应状态观测器预测定常海流成分,用于补偿定常海流的影响.同样地,Borhaug等[5]在LOS中加入另一种积分项,并对系统的全局稳定性给出了严密的证明.
路径跟随控制的另一大挑战是船舶运动的动力学模型参数随着自身状态、航行环境和外界干扰(速度、装载情况、水深以及风、浪、流作用等)的变化而改变,这对控制器的自适应能力或鲁棒性提出了更高的要求[6].许多学者在该领域开展了研究.Fossen等[7]使用ILOS以及滑模控制方法设计了间接和直接自适应路径跟随控制器;Liu等[8]综合应用神经网络和动态面控制方法,并考虑控制输入饱和的影响,解决了直线和曲线路径跟随问题;刘洋等[9]针对船舶模型参数不确定性和控制增益未知的非线性船舶航向控制问题,使用RBF神经网络逼近航向控制律;罗伟林等[10]采用神经网络对控制模型中的建模误差予以在线辨识和补偿,避免了对建模误差界定函数的经验选择.秦梓荷等[11]为实现对船舶速度的光滑控制,在滑模控制中引入了低通滤波器,以抑制因外界干扰和滑模切换面自身引起的横荡与艏摇速度的高频振荡.
本文首先对传统的LOS方法进行改进,加入漂角项并引入关于漂角的自适应状态观测器,以消除未计及漂角带来的稳态误差影响,使得在横向偏差为0的情况下仍可能产生一个不同于预设路径方向的参考航向,因此同时也可用于抵抗海流的影响;其次,采用滑模控制实现对参考航向时历曲线的跟踪,并使用神经网络拟合控制模型的建模误差及环境扰动,以增强控制系统的自适应能力;最后,建立仿真模型(包括波浪干扰力模型)进行了仿真研究,验证了本文所提出方法的有效性.
1 LOS制导方法
1.1 传统LOS制导方法
采用如图1所示的两个右手直角坐标系,即惯性坐标系O0-x0y0z0和船体坐标系Ob-xbybzb,来描述船舶在水平面内的操纵运动.本文只考虑对直线路径的跟随问题,为了简化表达,将惯性坐标系原点O0取在预设航线的起点位置,x0轴朝向预设的航线方向,z0轴垂直向下为正;船体坐标系原点Ob固定在船体重心,xb轴指向船艏,yb轴指向船体右舷.
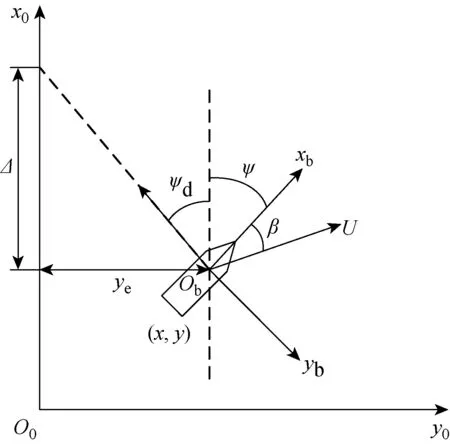
图1 LOS制导示意图Fig.1 Schematic of LOS guidance
图1中,Ψ为船舶的艏向角,定义从x0轴顺时针旋转至xb轴为正;β为漂角,定义从xb轴顺时针旋转至速度方向为正;(x,y)为船舶重心在惯性坐标系下的位置坐标;ye为船舶的横向偏差,ye=y;Δ为前视距离,是LOS制导算法中可调的设计参数,一般为船长量级;Ψd为制导的视线方向(参考航向),具体的表达将在下文中给出.
通过LOS制导方法可将路径跟随问题转化为对参考航向的跟踪问题,其控制目标是船舶能够在恒定航速下收敛至预设路径.船舶在水平面内运动的3自由度运动学模型为
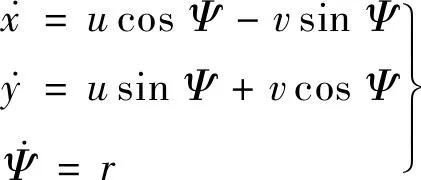
(1)
式中:u、v、r分别为船体坐标系下的前进速度、横移速度以及转艏角速度.
在传统LOS制导方法中,生成的参考航向为
(2)
结合图1可见,Δ越小,船舶收敛至预定路径越快,但同时会引起较大的超调量以及稳定时间.
1.2 漂角状态观测器
传统LOS制导方法未考虑船舶漂角的影响,在横向偏差为0时,生成的参考航向也为0°,但此时的漂角不一定为0°(即存在一定大小的漂角);在海流、波浪等环境干扰下,船舶最终也会存在一定的漂角.这些都会导致船舶不能稳定收敛到预定路径,而是出现一个稳态横向偏差(此时船速方向与预设路径方向平行,而实际航向与制导产生的参考航向相同).因此需要在LOS中加入漂角项,得到
(3)
然而漂角不易测得,某些船舶也无法获取其速度信息;有些船舶虽然可以测量得到速度信息,但传感器价格昂贵,或者测量时容易混入噪声.为此,本文通过设计关于漂角的自适应状态观测器来预测船舶漂角,以在LOS制导律中加入积分环节,消除环境干扰带来的稳态横向偏差.
将式(1)的第2式改写为
(4)
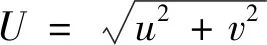
船舶的漂角会影响横向偏差的稳定,因此选取漂角与横向偏差作为状态变量,设计以下自适应状态观测器(根据Lyapunov稳定性判别方法进行反推设计得到):
(5)

引入状态观测器后,LOS生成的参考航向更新为
(6)
即有
由此可以看到,引入漂角状态观测器实质上是在LOS制导律中加入了积分环节,这将有助于提高控制器的自适应能力,使得改进后的LOS能够抵抗一定程度的缓慢时变的环境扰动力影响.
结合式(4)和(6),可以得到:
(7)

(8)
自适应状态观测器的动态误差为
(9)
选择候选Lyapunov函数:
(10)
式中:k4、k5为设计参数,取值为正.
对式(10)求导可得:

(11)

(12)
2 航向控制器设计
2.1 转艏动力学模型
通常采用Nomoto模型来描述船舶的转艏动力学过程.一阶非线性Nomoto模型可以表示为[12]
(13)
式中:K和T为操纵性指数;HN(r)为关于转艏角速度r的非线性函数;δ为舵角.
2.2 径向基函数神经网络
本文采用径向基函数(RBF)神经网络来拟合非线性函数HN(r).RBF神经网络是一种三层神经网络,输入层到隐含层的映射是非线性的,而隐含层到输出层的映射是线性的.对于非线性函数f(Z),可用以下公式描述[13]:
f(Z)=WTH(Z)
(14)
式中:Z∈Rn为输入向量,n为输入层神经元数;W∈Rl为权重向量,l为隐含层神经元数;H(Z)=[h1(Z)h2(Z) …hl(Z)]T是隐含层输出.选择高斯函数作为径向基函数:
(15)
i=1,2,…,l
式中:μi=[μi1μi2…μin]为中心点;σi为方差.研究表明[13],式(14)可以以任意精度逼近任意的非线性函数:
f(Z)=W*TH(Z)+ε
(16)
式中:W*为理想的权值系数;ε为估计误差.
定义损失函数为
(17)

(18)
2.3 滑模控制
将式(13)改写为
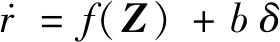
(19)
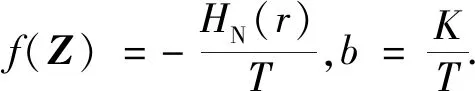
以下采用滑模控制来实现船舶的航向控制[14].首先定义一个滑模面:
S=c(Ψ-Ψd)+r
其中:c为设计常数.则有:
(20)
对式(6)求导,可以得到:
(21)
考虑系统的稳定性,下面利用Lyapunov稳定性判据来进行舵角控制律的设计.选取Lyapunov函数:
(22)
对式(22)求导,并将式(19)~(21)代入求导后得到的公式,可得:
(23)
滑模控制律可分为等效控制律和转换控制律两部分:
①优点:具有高延伸性、高抗拉性、高抗弯曲性的技术特性;管件电阻较大,不易产生电腐蚀,耐腐蚀性强;采用承插接口,柔性接头,承受局部沉降能力好;工作寿命长(一般50~100 年);管壁薄、重量轻(DN900 mm重量 0.28 t/m);价格适中(DN900 mm单价1 866元/m)。
δ=δeq+δsw
(24)
设计以下等效控制律:
(25)
将式(24)和(25)代入式(23),可得:
(26)
设计以下转换控制律:
(27)
式中:k6为正的设计参数.
再将式(27)代入式(26),得到:
(28)

3 仿真结果及分析
3.1 船舶运动数学模型
在此只考虑船舶所受的水动力以及波浪力,而忽略环境中风与海流的影响(事实上,缓慢时变的风载荷与流载荷可以等效地并入二阶波浪漂移力中),水面船舶三自由度操纵运动的Abkowitz模型为
(29)
式中:m为船舶质量:xg为船舶重心纵向坐标:IZ为绕过船舶重心垂直轴的惯性矩;Xhyd,Yhyd,Nhyd为水动力;Xwave,Ywave,Nwave为波浪力.
以Mariner实船为研究对象来验证前文所设计的控制器的控制效果,船长Lpp为160.93 m,设计航速为15 kn,水动力的具体表达形式以及其中的无因次水动力导数参见文献[15].
3.2 波浪力建模
在运动控制系统的仿真中,加入波浪力的影响可以检验控制器的鲁棒性.一般将波浪力分为一阶高频波浪力和二阶慢漂波浪力进行建模.参考文献[12],用二阶传递函数对波浪力及力矩进行建模,对于考虑三自由度运动的水面船舶有:
(30)

将二阶波浪慢漂力di(i=1,2,3)建模为缓慢时变偏差项:
(31)
式中:wi(i=4,5,6)也为随机的零均值高斯白噪声.


图2 无因次二阶及一阶波浪力矩Fig.2 Nondimensional second-order and first-order wave moments
3.3 数值仿真结果
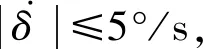



图3 航向控制仿真结果Fig.3 Simulation results of heading control
3.3.2自适应观测器的有效性 再验证NN-SM路径跟随控制算法中自适应漂角状态观测器的有效性.引入该观测器实际上是在LOS中加入积分环节,可以通过在二阶慢漂波浪力(非零缓变成分)干扰下的仿真试验来检验观测器的有效性.在此对预设路径y0=0进行跟随,初始状态设为 (x,y,Ψ)=(0,200 m,0°),并将NN-SM路径跟随控制结果和PID控制结果进行对比,PID控制参数设置同上.

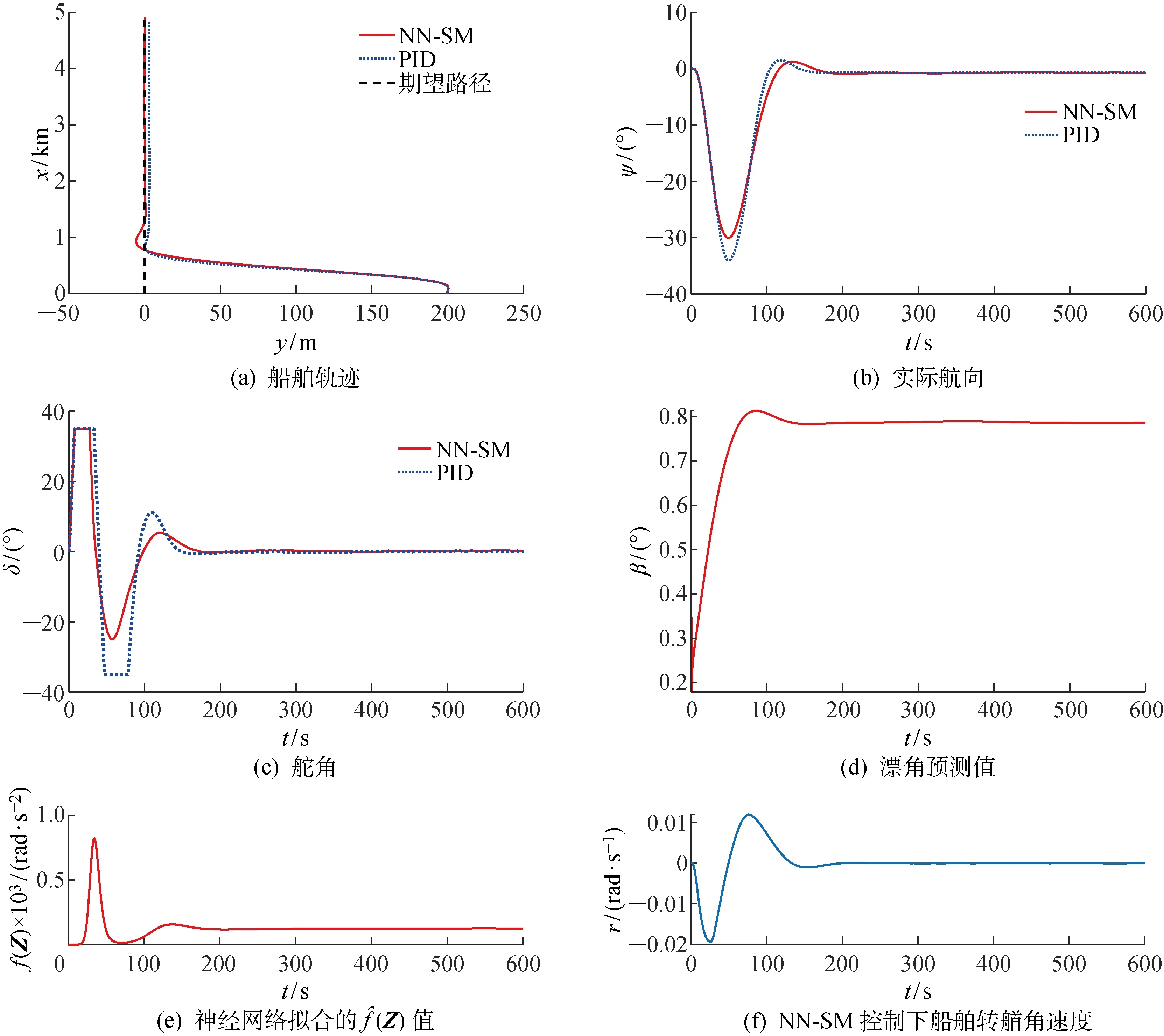
图4 二阶波浪力作用下路径跟随仿真结果Fig.4 Simulation results of path following under the second-order wave forces
3.3.3路径跟随控制器的有效性 通过在一阶高频波浪力(零均值)作用下的仿真试验来检验路径跟随控制器的有效性,仿真结果如图5所示.在一阶高频波浪力作用下,船舶仍能跟踪直线路径,说明控制器在抑制高频波浪力的影响方面是有效的.

图5 一阶波浪力作用下路径跟随仿真结果Fig.5 Simulation results of path following under the first-order wave forces
4 结论
本文提出了一种欠驱动水面船舶的自适应路径跟随控制器,使用LOS制导策略将对位置与航向的控制转化为单一对航向的控制,解决了欠驱动问题.仿真结果表明,通过在LOS中引入漂角状态观测器,能较好地预测船舶漂角,其积分作用可使船舶抵抗二阶慢漂波浪力的干扰.本文所提出的方法在欠驱动船舶(尤其是只能依靠航向信息操舵而无速度信息反馈的船舶)的运动控制问题中具有较强的实用性.
为了应对控制模型的不确定性问题(建模误差和环境扰动),利用RBF神经网络并结合滑模控制来实现航向控制,仿真结果表明设计的航向控制器具有较好的自适应能力.此外,在一阶高频波浪力的干扰下,该控制器仍能有效地使船舶跟随预设路径,表明其具有较好的鲁棒性.
