基于高斯过程回归的车辆巡航系统学习预测控制

何德峰，彭彬彬，顾煜佳，余世明

(浙江工业大学 信息工程学院，杭州 310023)

随着人们汽车保有量的增加，道路拥堵、环境污染、能源消耗、交通安全等问题越来越严重.作为传统巡航系统的增强技术，自动巡航控制(ACC)系统可通过控制节气门开度和制动系统自动调整车速，提高驾驶舒适性和安全性[1-2]，是目前智能交通系统的重要内容之一.早期ACC系统可以采用PID控制算法实现ACC系统的定速巡航和定距控制，文献[3]采用PID控制算法调整ACC系统的间距误差和相对速度，并通过零极点配置方法选取合适的控制参数.

随着对ACC系统研究的不断深入，研究人员希望在满足定速、定距巡航控制需求的基础上对驾驶的性能进行改善.由于模型预测控制(MPC)具有显式处理系统约束以及多变量的优点[4-6]，近年来被广泛地应用于ACC系统：文献[7]提出了3种基于MPC的ACC方法，并在文献[8-9]中做了进一步的应用验证；文献[10]针对前车信息跳变问题，提出车间反应时距的策略，结合MPC算法可有效减少ACC模式切换产生的加速度突变，提高乘车舒适性；文献[11]针对前车驶入驶出工况，实时调整MPC权重以提高燃油经济性和乘车舒适性.传统MPC假设是在预测时域内前车加速度不变的情况下预测前车加速度信息，但在实际情况中难以实现.当前车加速度不断变化时，由传统MPC所求得的最优解会产生偏差，对此，文献[12]采用闭环控制策略以补偿前车加速度变化的影响，改善了预测和控制效果.文献[13]将前车加速度看作一时间序列数据，比较了时间序列数据预测常用的参数化和非参数化方法，结果表明高斯过程回归方法具有更好的预测效果[14].

考虑车辆自动巡航系统前车加速度预测问题以及对安全性、舒适性和经济性要求，本文采用高斯过程回归方法对前车加速度进行学习建模，结合车间运动学模型实现前车加速度及驾驶状态的预测计算.再通过在线滚动优化车辆安全性、舒适性和经济性综合指标，设计了一种基于高斯过程回归的车辆自动巡航系统学习预测控制器.最后，结合CarSim/Simulink联合仿真平台和加减速典型驾驶工况，仿真验证了所提出的巡航控制方法.相比传统基于MPC的车辆巡航控制方法，本文方法具有更好的舒适性及更小的燃油消耗.

1 自适应巡航系统车间运动学模型

图1所示为自适应巡航系统自车和前车的纵向运动学关系，并定义

图1 车辆跟踪场景Fig.1 Tracking scenario of vehicles considered

(1)

式中：Δd为车间距误差；d为两车实际车间距；ddes为理想安全车间距；Δv为相对速度；vp为前车速度；vh为自车速度；xp为前车位置；xh为自车位置；th为车间时距；d0为最小固定车间距；ah为自车加速度；τd为时间常数；ades为期望加速度.

取车间距误差d、相对速度v、自车加速度ah作为状态变量x；期望加速度ades为控制输入u；将前车加速度ap看作系统扰动w；车间距误差d、相对速度v、自车加速度ah为系统输出y，得到的状态空间模型为

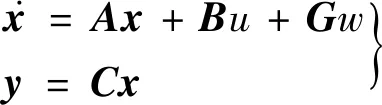
(2)

(3)

对式(2)所建立的状态空间方程进行离散化后，可以得到

(4)

(5)

式中：k为当前采样时刻；k+1为下一采样时刻；Tc为采样周期.

2 前车加速度高斯过程预测

在k时刻测得前车的p个历史时刻k-p,k-p+1,…,k-1的加速度分别为ap(k-p),ap(k-p+1),…,ap(k-1).令

(6)

此时将K和Ap当作训练集的输入和输出，其中假设Ap是服从高斯分布的，即

Ap=F(K,K)～N(μ(K,K),σ(K,K))

(7)

式中：μ(K,K)为F(K,K)的均值矩阵，将μ(K,K)设为0；σ(K,K)为F(K,K)的协方差矩阵，可通过协方差函数m(ka,kb)计算得到；ka,kb∈K，其中协方差函数m(ka,kb)选择平方指数函数型，即

(8)

(9)

0.5lg|σ(K,K)|-0.5plg (2π)

(10)

式(10)是一个非凸的优化问题，可采用牛顿法和共轭梯度法求取θ的最优值[15-16].

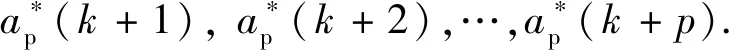
(11)

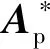
N(μ(K*,K*),σ(K*,K*))

(12)

(13)

计算测试集输入K*的协方差矩阵σ(K*,K*)，即

(14)

计算测试集输入K*与训练集输入K的协方差矩阵σ(K*,K)，即

(15)

参照式(13)联合高斯分布，根据高斯分布性质可以得到F(K*,K*)的条件分布F(K*,K*)|F(K,K)，即

F(K*,K*)|F(K,K)～

N(σ(K*,K)σ(K,K)-1Ap,σ(K*,K*)-

σ(K*,K)σ(K,K)-1σ(K*,K)T)

(16)

(17)

当在下一时刻k+1时,重新测得前车的新历史p个时刻的加速度值.重复上述步骤，即可在下一时刻来预测新未来p个时刻的前车加速度值，同时取预测值的第一个作为下一时刻的预测参考值.如此周而复始，即可实现在线预测前车加速度的值，并不断修正预测偏差.

3 基于高斯学习的预测巡航控制算法设计

将式(4)建立的自适应巡航系统车间运动学模型作为预测模型，对自适应巡航系统的未来行为进行p步预测，定义p步预测输出向量和p步输入向量[17]分别为

(18)

考虑到高斯过程回归预测的前车加速度扰动值，在这里定义p步加速度干扰项为

(19)

那么，对系统未来p步预测的输出可表示为

(20)

结合式(11)和(17)进一步展开可得到

Sxx(k)+SuU(k)+

Sdσ(K*,K)σ(K,K)-1Ap

(21)

(22)

稳态跟车工况中，期望车间距误差Δd，相对速度Δv同时趋于0，自车加速度能跟上前车加速度.因此可将优化目标写成一个加权形式的值函数[18]：

u(k+j)Ru(k+j)=

(23)

进一步考虑车辆的物理特性以及汽车行驶过程中的乘车舒适性要求，定义车辆速度和期望加速度约束：

vmin≤v(k)≤vmax，umin≤u(k)≤umax,∀k≥0

则在当前时刻k，定义车辆自动巡航系统滚动时域优化控制问题

(24)

s.t.x(j+1|k)=Akx(j|k)+

Bku(j|k)+Gkw(j|k)

y(j|k)=Ckx(j|k)

w(j|k)=σ(K*,K)σ(K,K)-1Ap

vmin≤v(j|k)≤vmax

umin≤u(j|k)≤umax

x(0|k)=x(k)

j=0,1,…,p-1

式中：整数p>0为预测时域；x(k)为车辆自动巡航系统在当前时刻k的状态；•(j|k)表示在时刻k对变量•在时刻k+j的预测值；Ap为根据式(6)求得的前车p个历史加速度值.根据式(24)得到控制序列U*(k)，将其第一个控制分量u*(0|k)作用于车辆自动巡航系统(4)；在下一时刻，重复上述运行过程，实现对车辆自动巡航系统的学习预测控制.

4 仿真与结果分析

在CarSim软件中搭建整车模型和仿真工况，前车和自车选取C级掀背式轿车，前轮驱动，发动机功率为125 kW，前车的速度设置为vp=v0+5.6sin(0.5t)，v0为前车的初始速度设为15.3 m/s，自车初始速度vh设置为13.9 m/s，两车初始距离相距40 m.在Simulink中搭建好控制系统模型，采用本文提出的算法，选取参数th=2 s、τd=0.2、p=10、Q=5I、R=10、Tc=0.1 s、umin=-4 m/s2、umax=5 m/s2、vmin=0和vmax=30 m/s，同时与传统模型预测控制算法(即在预测时域内前车加速度假定恒定)作对比，仿真结果如图2～5所示.

图2 本车加速度曲线Fig.2 Acceleration of host vehicle

图3 本车速度曲线Fig.3 Speed of host vehicle

从图2和3可得，当前车加速度不断增大时，由于传统MPC方法假定在预测时域内前车加速度不变，所以预测输出会偏小导致自车加速度偏小，故车速没有基于高斯过程回归的MPC方法的车速快.当前车减速度在不断减小时，由于传统MPC方法假定在预测时域内前车减速度不变，所以预测输出会偏大，导致自车减速度偏大，车速下降更剧烈.加入加速度预测后，自车能提前做好加减速的准备，避免了不必要的急加急减，速度变化更平缓，峰值更低，跟踪效果更理想.此外，采用上述高斯过程回归预测方法，能有效地预测前车加速度变化.

如图4所示，相对于传统方法，在基于高斯过程回归的车辆自动巡航系统学习预测控制方法下，当前车不断加速时，两车相对距离会更小，交通容量更大；当前车不断减速时，两车相对距离会更大，以确保行车安全.如图5所示，基于高斯过程回归的车辆自动巡航系统学习预测控制方法可使车辆燃油消耗减少.

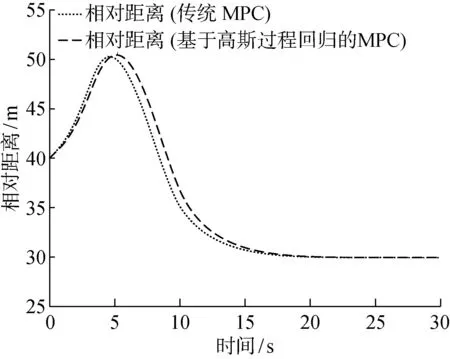
图4 车间距实时曲线Fig.4 Time evolution of inter-vehicle distances

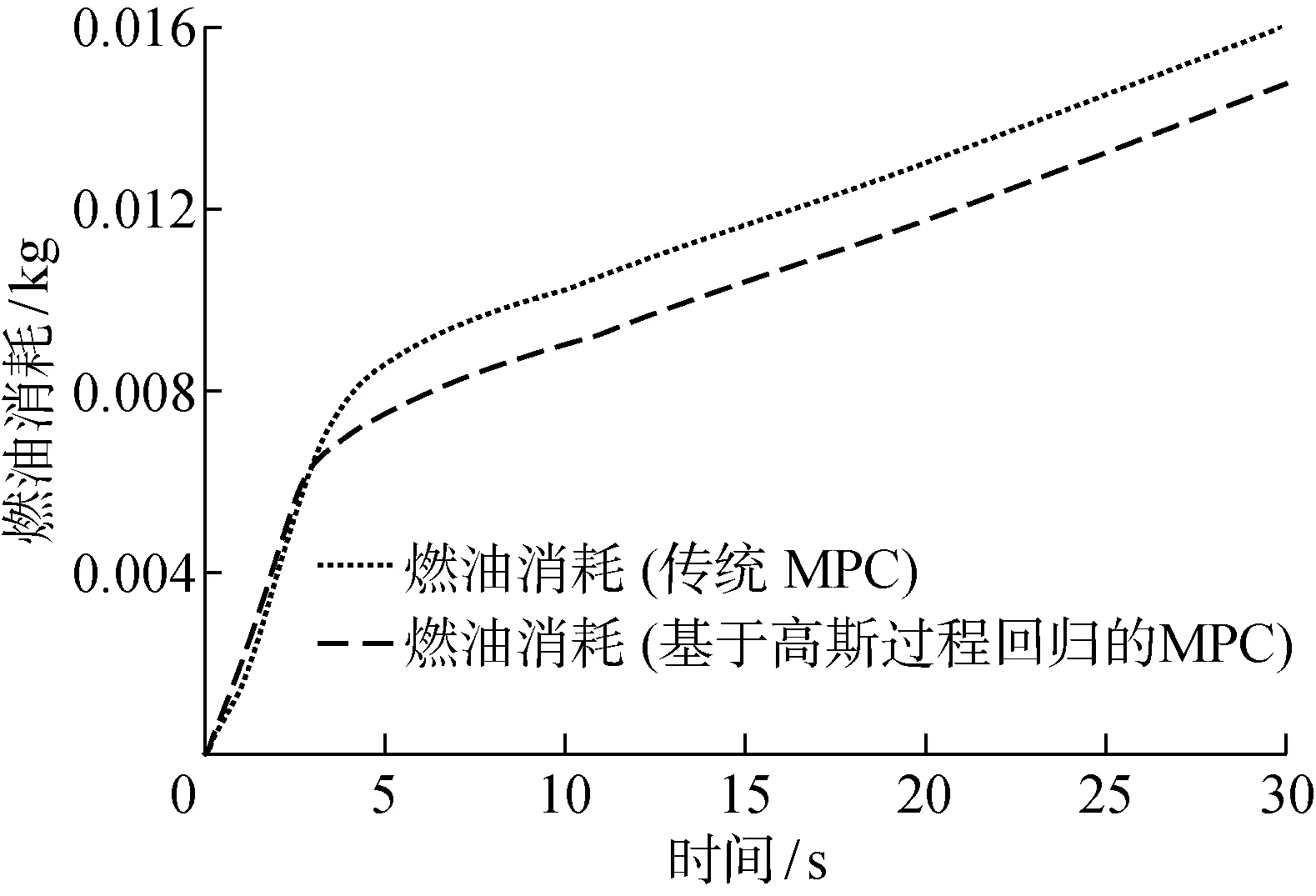
图5 本车燃油消耗实时曲线Fig.5 Time evolution of fuel consumption of host vehicle

5 结语

本文针对车辆自动巡航控制系统中前车加速度预测问题，以及为满足人们对安全性、舒适性和经济性要求，提出了一种基于高斯过程回归的车辆自动巡航控制系统学习预测控制策略.通过对前车加速度基于高斯回归的学习建模，预测在优化时域内的前车加速度，结合车间距运动学模型以及在线滚动优化安全性、舒适性和经济性综合性能指标，设计了车辆自动巡航控制系统学习预测控制器.仿真结果表明，与传统模型预测巡航控制策略相比，本文控制策略下的车辆乘车舒适性以及燃油经济性均得到有效提升.