基于航向约束的无人艇位姿保持制导策略
2020-10-12李朋博苑明哲肖金超熊俊峰
李朋博,苑明哲,肖金超,熊俊峰
(1.中国科学院沈阳自动化研究所,沈阳 110016;2.广州中国科学院沈阳自动化研究所分所, 广州 511458;3.中国科学院大学,北京 100049)
随着现代控制理论和智能控制技术的不断发展,无人艇智能水平得到了极大提高,推动了无人艇在多领域的广泛应用.目前在无人艇-无人机和无人艇-水下机器人协作系统中,当无人机或水下机器人等子系统进行回收时,作为母体的无人艇应保持固定的位姿为子系统提供稳定的回收平台.位姿保持是指系统的位置和姿态持续稳定或可快速回到稳定状态.然而无人艇作为典型的欠驱动系统,无法依靠自身推力系统同时实现自身的前向、侧向和转首运动[1].当无人艇受到风浪流等扰动产生位姿变化时,尤其是受到扰动发生较大横荡时,欠驱动无人艇无法像全驱动船舶依靠动力分配策略在在侧向施加动力,也无法依靠传统控制律兼顾其欠驱动特性,只能依靠前向和转首运动改变无人艇位姿,难以兼顾首向角保持或位置保持效果.因此,如何兼顾欠驱动特性已成为无人艇位姿保持研究的关键难题.
当前,学者解决无人艇位姿保持问题多采用传统控制理论和深度学习等智能方法.采用传统控制理论方法,主要基于非线性控制律.文献[2-3]针对风扰动问题,设计了自适应前馈控制器,并将滑模控制器应用于无人艇,降低了风扰动对位姿保持的影响,位姿保持效果较好.文献[4]设计了基于干扰观测器的鲁棒位姿控制系统,由干扰观测器对干扰建模误差给出补偿,有效减小了干扰对水下机器人位姿保持的影响.目前也有基于深度学习和视觉等智能方法的无人艇位姿保持控制方法研究,文献[5]提出了无模型的深度强化学习算法在水下航行器的6个自由度保持中的应用,平衡了计算的易处理性和性能,使系统可以迅速响应,但仍旧无法保持航向角的稳定.文献[6]创新地提出了一种视觉导航方法,通过CIALAB和k均值方法进行波峰检测并制定导航策略,从而实现系统的位姿保持.文献[7-8]针对无人艇不同行为设计了切换控制器,基于性能的监督切换控制系统指示控制器之间的切换以提高闭环性能,减小了在位姿保持时控制器切换带来的位姿误差.
目前,基于非线性控制器的位姿保持无法有效兼顾无人艇的欠驱动性,且控制器设计相对复杂.深度学习训练数据集大,训练集外的场景控制效果差;视觉等其他方法的响应速度慢,实时性有待提高.针对以上问题,本文提出了一种基于航向约束的位姿保持制导策略,通过将航向约束纳入外环制导,无人艇在不同区域执行不同的行为策略,生成的位姿期望与内环控制相结合,实现无人艇的位姿保持.相比于常规控制器,制导策略在执行过程中严格约束了航向角,降低了控制器设计的难度,同时兼顾了无人艇的欠驱动特性,简化了控制器设计.
1 问题描述
无人艇作为典型的欠驱动系统,其系统输入维数少于控制输出维数,即只依赖前向动力和偏航力矩控制无人艇的运动状态,因而无法同时控制无人艇的前向、侧向和转首运动.图1所示为无人艇的3自由度平面运动模型.

图1 无人艇运动模型:船体固定坐标系ObXbYb和惯性坐标系OEXEYEFig.1 Motion model of USV:body-fixed coordinate system ObXbYb and inertial coordinate system OEXEYE
无人艇具有6个自由度的复杂运动,往往难以建立精确的6自由度模型.为简化研究,本文不考虑无人艇的纵摇、横摇和升沉运动,只建立无人艇的纵荡、横荡和首摇3自由度耦合线性模型[9].建立的3自由度简化动力学模型为
(1)

系统在平衡点附近运动时,可看作线性模型,经简化得到考虑侧滑运动的一阶线性野本模型[1],推导过程参考文献[10]:
(2)
式中:Tr和Kr为船舶操纵性指数;δ为输入舵角;β为侧滑角;Tβ、Kβ为常数.欠驱动无人艇通常不配备侧向推进器,无法在Yb方向直接施加推力改变Yb轴方向位姿,而是通过前向运动和转首运动改变无人艇Yb方向位姿,因此无人艇无法以原路径返回期望位姿点.
2 基于航向约束的制导策略
基于航向约束的制导策略是指依据制导策略,对无人艇航向角施加约束,在整个过程中将首向角控制在偏差范围内,以此将航向约束由内环控制转为外环制导.当无人艇偏离期望位姿后,由外环制导根据当前位姿状态给出期望速度和期望航向角.下文将对制导策略作简要说明.
2.1 前提
本文只考虑在扰动场景下无人艇可控的情况.设定本文的航向角偏差范围为[-ψe,ψe],ψe为允许的误差角,期望位姿为(xd,yd,ψd),其中:xd、yd和ψd分别为期望纵向位移、横向位移和首向角;将任意时刻的位姿记为(x,y,ψ),x、y和ψ分别为任意时刻的纵向位移、横向位移和首向角.
2.2 位姿保持制导策略
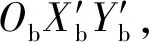
(3)
式中:(xE,yE,ψE)为无人艇在惯性坐标系下的位姿.
将固定坐标系划分为3个区域:可到达区域A、B和不可到达区域C.在可到达区域内,无人艇可依靠前向运动和转首运动回到期望位姿,避免由于无法侧滑导致首向角误差超出期望范围.同时设置容差半径Re,表示当无人艇在这个区域内时即视为其位置达到期望,容差带de是为了防止由于扰动影响在可到达区域A和不可到达区域C之间发生频繁的区域跳变,将容差带宽设置为可到达区域B.区域划分如图2所示.

图2 固定坐标系划分示意图Fig.2 Region-dependent segmentation of fixed coordinate system
可到达区域A定义为
A={(x,y)||x|≥|ytan(90°-ψe)|+de}
可到达区域B定义为
B={(x,y)||ytan(90°-ψe)|<
|x|<|ytan(90°-ψe)|+de}
不可到达区域C定义为
C={(x,y)||x|≤|ytan(90°-ψe)|}
令m为区域切换标记,初始化为0,定义为
C→B:m=1
B→A:m=0
2.2.2制导策略 如图3所示,无人艇受到外界扰动并偏离容差半径区域时,执行本文制导策略.

图3 策略流程图Fig.3 Flowchart of strategy
在区域A、B和C分别设置了不同的制导策略:当无人艇在位于不同的区域时,回到期望点的策略是不同的,本文将以无人艇位于第一象限为例进行说明.
策略1如图4所示,当m=0且位于区域A、B时,此时无人艇将直接以最终期望进行制导,整个过程中首向角均在期望误差范围内,因此直接制导可以返回期望.

图4 制导策略示意图——情形1Fig.4 Guidance strategy:situation 1
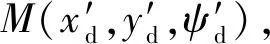
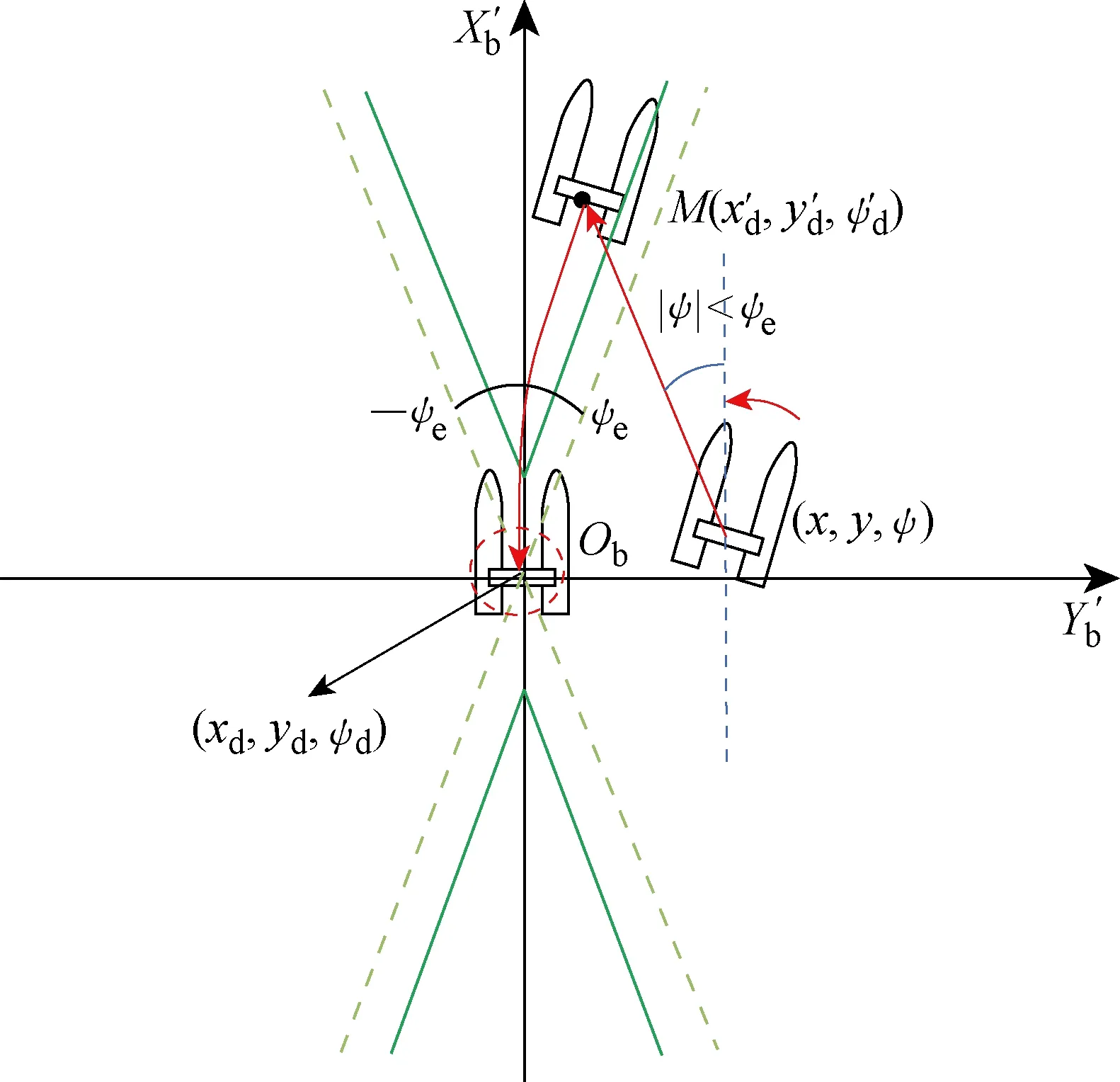
图5 制导策略示意图——情形2Fig.5 Guidance strategy:situation 2
将当前位姿设为(x,y,ψ),最终期望位姿(xd,yd,ψd),无人艇受到扰动偏离平衡后,位于不可到达区域C内时,需要执行策略2计算到达区域A的最短距离和期望位姿,计算当前至可到达区域A的最短距离:

(4)
式中:de为容差带高度,其作用为防止无人艇受限于自身回转半径或者受到环境扰动时,在区域切换过程中可能会出现频繁的区域跳变.

(5)
式中:θ=2ψ-Δ,Δ为容差角,由控制首向角控制的误差决定.
在制导方式上,采用视线法制导策略:
(6)
式中:xLos和yLos为期望点坐标.
3 仿真试验
3.1 仿真结构及相关参数
比例-积分-微分(PID)控制器是迄今最为常用的反馈控制形式,具有简单易用、鲁棒性强和适应性强等优点,因此本文采用PID控制器作为内环控制器,其控制结构如图6所示.

图6 位姿保持控制结构Fig.6 Control structure of station keeping
一阶线性速度动力学模型如下:
(7)
式中:ε为输入油门大小;a和b为速度方程参数.模型参数见表1[10].

表1 带侧滑的模型参数Tab.1 Parameters of model with sideslip
在MATLAB 2018a环境下进行仿真,在仿真实验中,加入扰动的解耦分量,各项速度上加入周期性扰动,同时加入利用MATLAB内置函数randn生成的随机数作为随机扰动.具体实验参数设置如表2.

表2 仿真实验的参数Tab.2 Parameters of simulation experiment
3.2 仿真实验
3.2.1仿真实验一 本文提出的基于航向约束的制导策略中,为了防止无人艇在制导过程中发生频繁的区域跳变,定义了容差半径Re和容差带高度de两个调整参数.在仿真实验中选取了不同的Re和de,图7所示为当Re=0.1 m,de=0.3 m时的仿真结果.从仿真结果可得,位置误差保持在一个较小的范围内.当由不可到达区域C穿过区域B到达区域A时,此时因为无人艇执行制导策略,导致部分仿真时刻出现XE向位移增大,致使整体位置误差变大,并且在整个制导过程中均会出现这种位置误差变化.仿真过程中,首向角误差长时间保持在期望误差ψ∈[-20°,20°]波动.
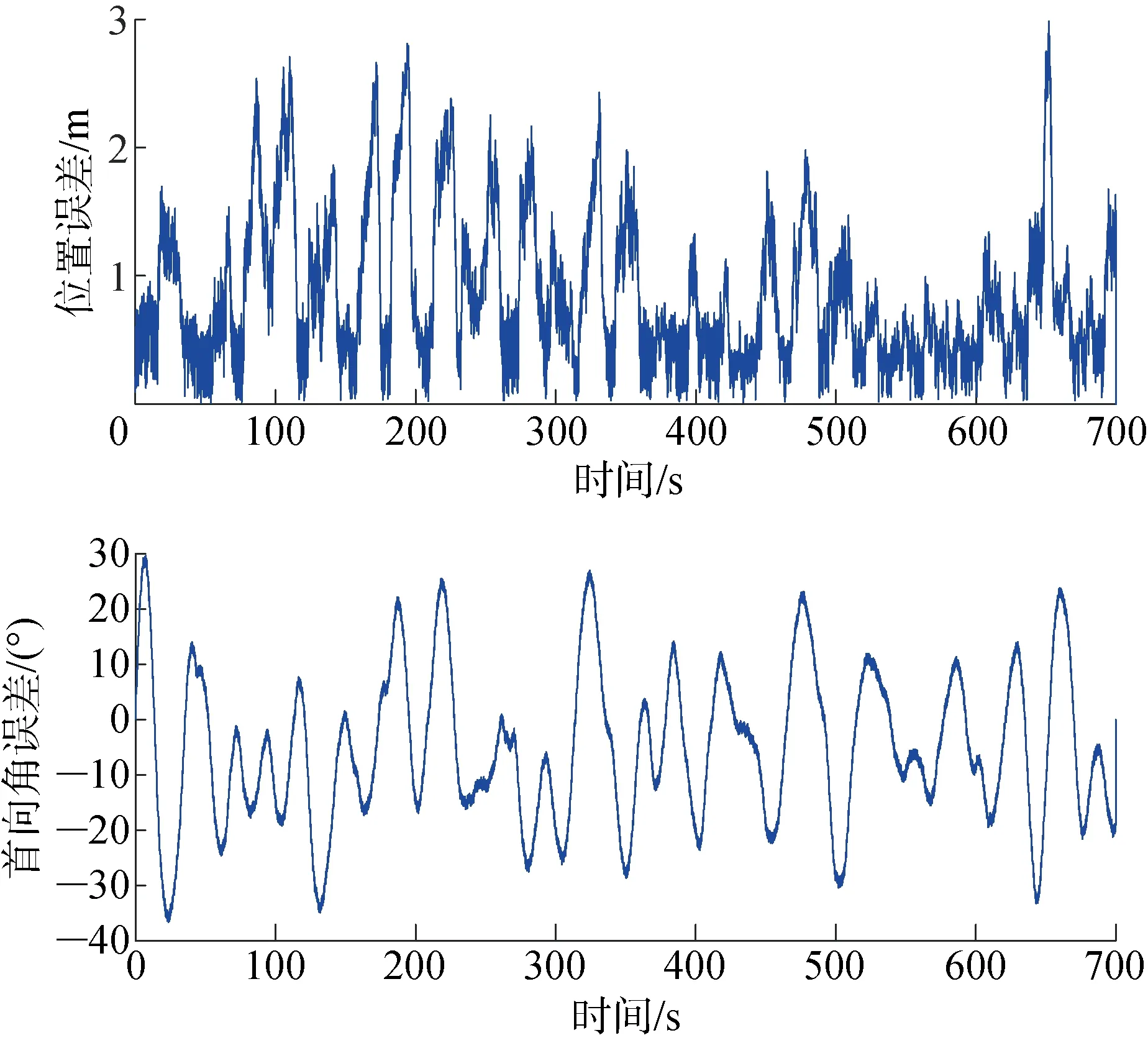
图7 当Re=0.1 m和de=0.3 m时的位置误差和首向角误差Fig.7 Position error and heading error at Re=0.1 m and de=0.3 m
受周期性扰动n1(t)、n2(t)和随机扰动的影响,在转向过程中由于转向能力不足致部分时刻的首向角越过期望误差角范围.表3所示为当Re和de取不同值时的位置误差和首向角误差.容差半径Re为0,即无人艇在期望位置附近,需要进行频繁制导,不断地改变自身位姿,导致位置和首向角不断变化.容差带高度de为0,会导致无人艇在区域切换时,发生频繁跳变.由于航向角变化过快,无法跟踪期望航向角跳变,前进后退控制困难.在低速下受环境干扰更大,会出现更大的位置偏差.当容差半径过大时,会由于容差带区域过大形成新的制导盲区,位置误差和首向角误差均有不同幅度的增大.逐渐增大容差带高度,首向角误差和位置误差无明显变化,是因为当容差带半径过大时,无人艇在容差带区域可以有足够的时间进行转向调整.容差半径和容差带高度的设置降低了在期望位置附近制导的频次以及执行机构的执行频次,有利于无人艇在期望位置附近保持状态稳定.由于无人艇进行位姿保持时是在低速状态下运行,推进器频繁的正反转切换会引起执行器过饱和,极易损坏执行机构.因此依据当前的制导策略,在实际进行容差带高度和容差半径设定时,容差半径的设定应当防止过大,容差带的设定应当防止过小,否则无人艇在环境干扰下,容易引起区域切换频繁导致的区域跳变,使得无人艇处于区域边界.

表3 不同Re和de下的位置误差和首向角误差Tab.3 Position error and heading error at different Re and de values
3.2.2仿真实验二 仿真实验二是本文提出的基于航向约束的制导策略与PD控制器对比仿真实验.在仿真实验中,设置了相同PD参数和相同的扰动.图8所示为当Re=0.1 m,de=0.3 m时,本文的方法和PD控制器通过仿真实验得到的一组对比结果.从图8(b)可以看出,本文方法的位置误差略大于PD控制器是由于执行制导策略时,无人艇向期望点M运动时导致位置误差偏大.从图8(b)可以看出,本文方法的首向角误差明显优于PD控制器是由于在制导策略中加入了首向角约束,致使首向角偏差明显减小.

图8 PD控制器和本文制导策略的位置误差和首向角误差对比(Re=0.1 m,de=0.3 m)Fig.8 Error for position and heading of PD controller and the guidance strategy proposed in this paper (Re=0.1 m,de=0.3 m)
进行了多次对比仿真实验,随机选择三组实验数据,结果如表4所示.从多次仿真结果可得,本文提出的基于航向约束的制导策略由于对实时航向施加约束,无人艇瞬时航向保持在期望范围内,无人艇首向角得到约束,因此首向保持效果更好.本文方法中的位置偏差相比PD控制器,会出现局部增大,这是由于本文制导策略下由区域C到穿过区域B最终到达区域A时引起的正常位置误差变化.考虑整体无人艇的首向和位置保持效果,认为增大的位置误差是可以接受的.因此,由仿真实验结果可以得出,本文提出的基于航向约束的制导策略相对传统的PD控制器具有更好的位姿保持能力.

表4 本文制导策略与PD控制器仿真对比Tab.4 Simulation comparison of PD controller and the guidance strategy proposed in this paper
4 结语
本文针对欠驱动无人艇位姿保持问题,提出了基于航向约束的无人艇位姿保持制导策略.将航向约束纳入外环制导,依据无人艇当前位姿执行相应的制导策略,给出符合期望的航向.通过内环控制器生成执行量,最终可以使无人艇返回期望位姿.相较于常规控制律,将首向角控制放入制导环,外环制导约束与内环控制约束相结合以兼顾欠驱动特性.实验一中仿真不同制导参数下的位姿保持实验,验证了本文方法的可行性.实验二仿真本文方法和常规PD控制器的对比实验,本文方法在航向约束的位姿保持过程中,无人艇具有更好的首向保持效果,验证了本文方法的有效性.
在仿真过程中虽引入了周期性扰动以及随机扰动,但在实际作业环境下,一方面需要对风浪流进行建模;另一方面,由于系统的位姿保持是在低速运动下进行的,需要提升低速运动状态下的无人艇控制精度以及无人艇进行前进和倒退的控制优化.
