绳牵连物体的运动研究

王维国

(江苏省海安高级中学，江苏 海安 226600)

绳杆关联系统是力学中的经典问题，对中学生来说是一个难点，在高考中屡见不鲜，也引起了一些研究者的关注．在研究绳杆关联系统速度和加速度关系时，不少人利用运动的合成与分解规律分析，或在直角坐标、自然坐标、极坐标下，用高等数学方法对几何关系式、速度关系式求导.[1]有研究者指出转动的绳牵连两物体的速度并非同时达到最大，并计算了速度最大的位置.[2]有人用几何画板、MATLAB作出了绳杆两端物体的加速度等物理量随角度变化的图像.[3，4]有的文献提及可用数值求解拉氏方程得到速度加速度和张力随时间变化，但没有详述．[5]而对绳牵连物体的运动量随时间变化规律定量关系的研究却未见到.本文对此及相关问题进行系统的分析，并将结论用图像进行直观呈现．

1 问题的由来

以某市2020届高三第一次调研试卷中的一道选择题为例.

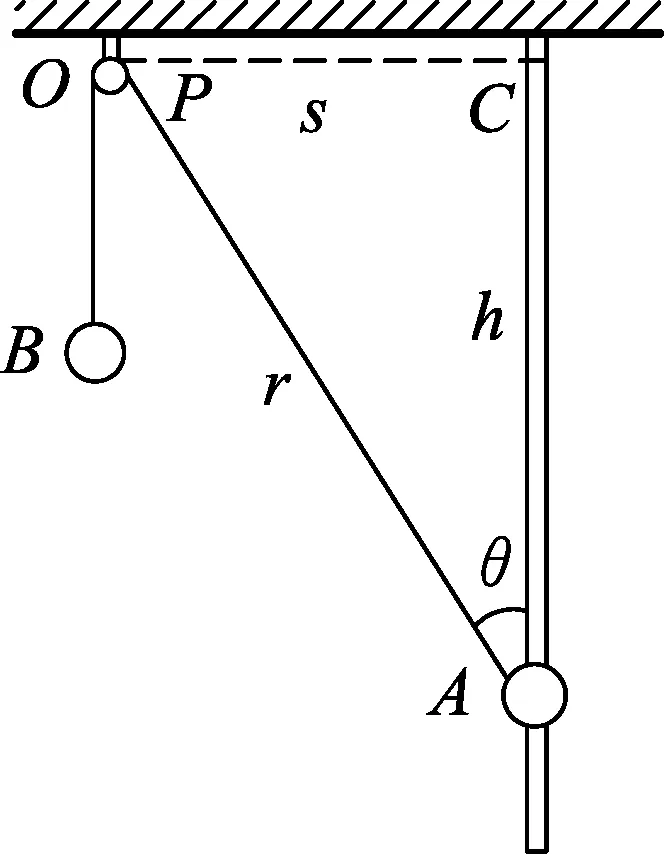
图1

例1.如图1所示，竖直杆上套有一个质量为m的小球A，用不可伸长的轻质细线通过轻质小定滑轮O，连接小球A、B．小球A从细绳与竖直方向的夹角为37°的位置由静止释放，恰能运动到细绳与竖直方向垂直的C点，一切阻力不计，已知sin37°=0.6.则

(A) 小球A在上升过程中加速度先减小后增大.

(B) 小球B在最低点时加速度和速度都为0.

(C) 小球B的质量为1.25m.

(D) 小球B的质量为2m.

答案： (A)、(B)、(D)．

不少教师对选项(B)有疑问，认为小球B从最高点开始运动先加速后减速，在最低点速度为0，而后向上做往复运动，所以在最低点时小球B加速度应该向上，而不为0．

本文就这个绳牵连物体问题从多个角度进行定量分析．

2 牵连加速度关系

因为张紧的刚性绳的总长度不变，所以两端物体沿绳方向的速度大小相等．有学生据此进行知识迁移，认为沿绳方向的加速度大小也相等．这个结论能否成立，需经推理证明．

2.1 绳牵连加速度关系的推导

我们用两种方法分析两小球在任意位置加速度aA、aB大小的关系．

2.1.1 相对运动法

取与轻小滑轮相切右侧绳上的点为P点，设P点到竖直杆的距离为s，绳与竖直方向的夹角为θ．任意时刻A球相对P点做圆周运动，有切向加速度aτ和向心加速度an，则A球相对动点P的加速度aAP有

aAP=aτ+an.

(1)

A球和绳上P点相对地面的加速度分别为aA、aP，由相对运动加速度关系有

aA=aAP+aP.

(2)

设B球的加速度方向向下，则绳上P点的加速度沿滑轮切向(AP方向)，与B球的加速度大小相等，aB=aP．

将(1)式代入(2)式，把(2)式投影到绳AP方向，得A球在AP方向上的加速度

aAcosθ=an+aB，

(3)

其中向心加速度为

(4)

将(4)式代入(3)式得任意位置两球加速度大小关系

(5)

此式中，A球加速度向上为正方向，B球加速度向下为正方向．

2.1.2 对几何关系式求导

在一些文献中，研究加速度关系用高等数学方法时涉及到单位矢量的导数，较为繁琐．如果在描述几何关系时，避免用角度参量，就能使运算过程更为简单．

设A球到P点距离为r，A球到C点距离为h，由几何关系得

r2=s2+h2.

(6)

将(6)式两边对时间求导得

(7)

因为r、h均随时间减小，所有

(8)

将(8)式代入(7)式得

rvB=hvA.

(9)

将(9)式两边对时间求导得

(10)

-vB2+raB=-vA2+haA.

即

(11)

(12)

(12)式与上一节所讲的结果(5)式相同．

2.2 牵连加速度关系讨论

在零时刻，A球在最低点，B球在最高点，vA=0，vB=0，则aAcosθ=aB；当A球运动到最高点，B球最低点，vA=0，vB=0，仍满足aAcosθ=aB．在这两个位置，“沿绳方向的加速度大小相等”是成立的，其条件是绳没有转动．B球最低点时，A球运动到最高点，绳水平，A球的加速度aA=g，且cosθ=0，则aB=aAcosθ=gcosθ=0.上述试题中的(B)选项“小球B在最低点时加速度和速度都为0”是正确的．在绳两端的物体的速度均为0时，绳的角速度为0，因此就没有向心加速度，此时两端物体沿绳方向的加速度相等．而很多人想当然地认为“B球在最低点会向上运动，所以加速度方向应向上”，其实在往返运动中，速度等于0时，加速度是可以同时为0的．

3 两球会同时达到最大速度吗？

两球速度都从0起先增大到极大值，然后减小到0，做往复运动.有人认为两球速度会同时达到极大，下面就这个问题进行定量分析．

3.1 两球达到最大速度的先后问题分析

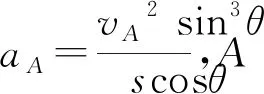
3.2 两球速度变化过程的图像分析

初始位置绳与竖直方向的夹角为θ0=37°，根据机械能守恒定律

(13)

得

mB=2mA=2m.

(14)

A从最低点运动到任意位置的过程中

(15)

vB=vAcosθ.

(16)

解得

(17)

(18)

将上式进行无量纲化处理，得

(19)

(20)

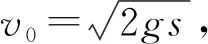
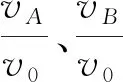
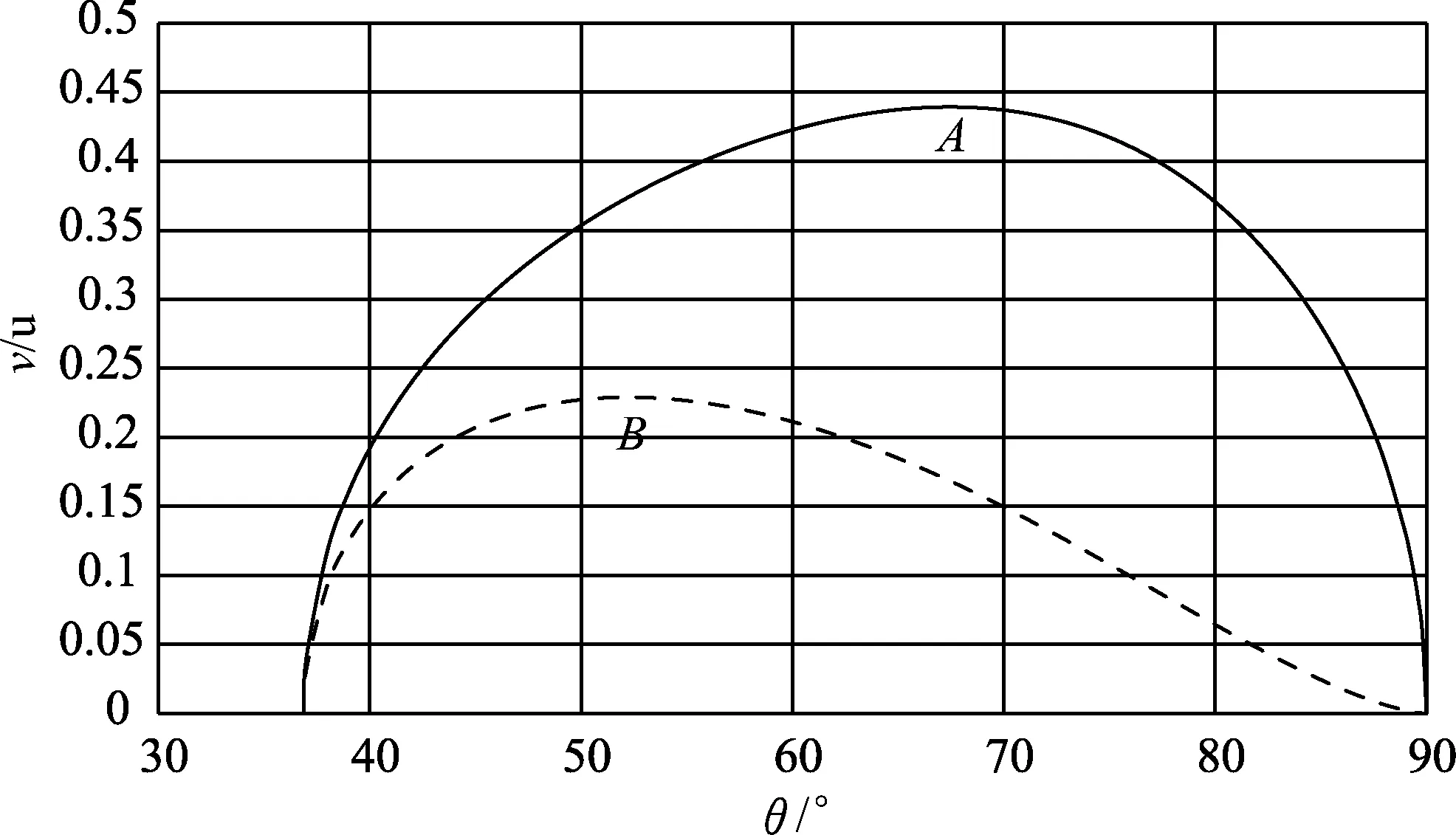
图2 速度随角度变化

从图2可知，在A球上升B球下降过程中，θ从37°增大到90°,当θ=52°时，B球的速度先达到极大值，θ=67°，A球的速度后达到极大值．用Excel的数值计算功能可得A、B两球速度先达到极大值的角度分别为52.2°和67.5°．在A球下降B球上升过程中，θ从90°减小到37°,A球的速度先达到极大值，B球的速度后达到极大值．

3.3 加速度随位置的变化情况

根据牛顿第二定律，有

Tcosθ-mg=maA.

(21)

2mg-T=2maB.

(22)

根据(12)、(17)-(22)式解得

(23)

(24)

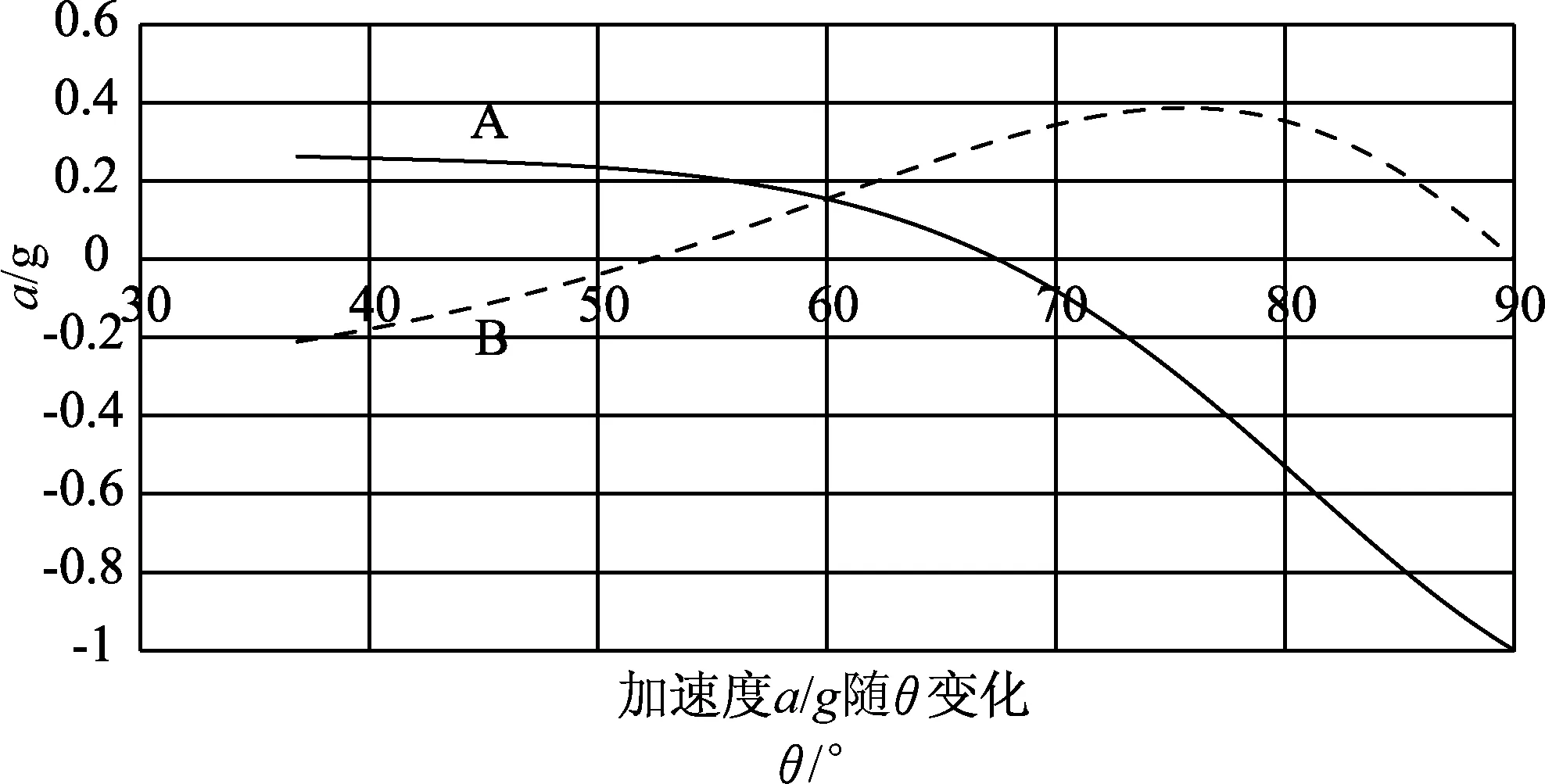
图3 加速度随角度变化

从图3可知，当θ=52°时，aB=0，B球的速度达到极大值，θ=67°时，aA=0，A球的速度达到极大值，与图2中位置一致．当θ=90°时，A球在最高点，vA=0，aA=g，B球在最低点，vB=0，aB=0，即B球的速度与加速度同时为0．

3.4 速度与加速度随时间的变化规律

由牵连加速度关系式写成微分方程，不易得到解析解．采用MATLAB程序，可以作出两球运动的速度随时间变化的图像．

由理论力学规律可知保守系的拉格朗日函数：[7]

L=T-V，

(25)

其中L代表体系的动能与势能之差，体系的动能为

(26)

(27)

拉格朗日量中势能的零势面对解没有影响.为方便表述，取A球的势能在C点时为0，B球的零势能面取B球运动的最低点下方s处，则体系的势能为

(28)

将(26)-(28)式代入(25)式得拉格朗日量为

(29)

保守力系的拉格朗日方程为

(30)

令广义坐标q(t)=θ，则广义速度q′(t)=ω，

(31)

(32)

最终方程为

(33)

化简后用MATLAB程序求解得到θ和ω，再代入下式中的速度关系．

(34)

设s=1 m，得到速率v随时间t变化图像，如图4所示图线A,B分别指vA,vB．

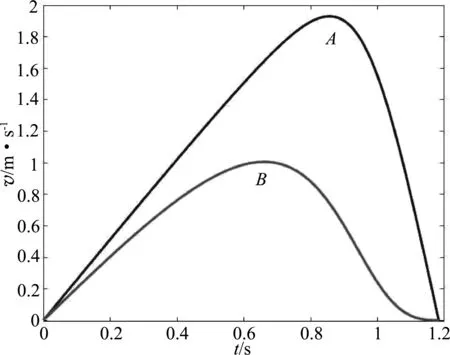
图4 v-t图像

从图4可以看出，在B球下降过程中，速度从极大值减小到0的过程中图像中存在一个拐点，加速度先从0起增大后减小到0，在B球速度为0时速率图线的切线的斜率为0，从另一个角度印证了选项(B)是正确的．

从图5可以看出，在B球下降过程中，加速度大小在两个时刻为0，一是速度为极大值时，另一个是速度减小到0时．

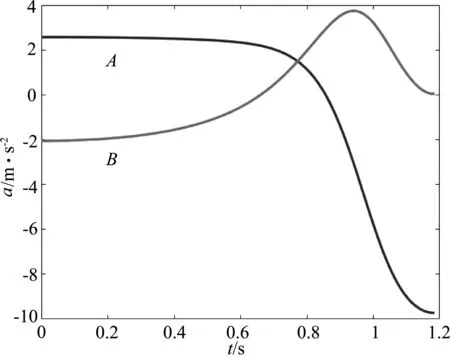
a-t图

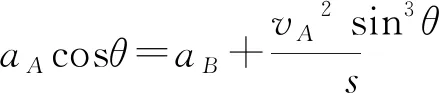
4 教学与命题建议

绳杆关联系统问题，常见诸高考试卷，如2018年高考江苏卷第15题.

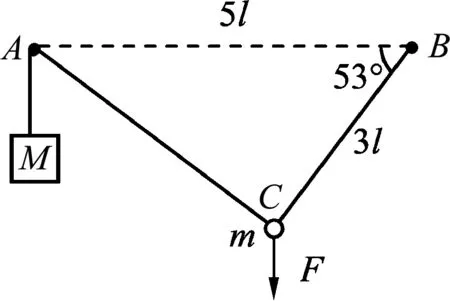
图6

例2.如图6所示，钉子A、B相距5l，处于同一高度．细线的一端系有质量为M的小物块，另一端绕过A固定于B．质量为m的小球固定在细线上C点，B、C间的线长为3l．用手竖直向下拉住小球，使小球和物块都静止，此时BC与水平方向的夹角为53°．松手后，小球运动到与A、B相同高度时的速度恰好为0，然后向下运动．忽略一切摩擦，重力加速度为g，取sin53°=0.8，cos53°=0.6．求：

(1) 小球受到手的拉力大小F；

(2) 物块和小球的质量之比M:m；

(3) 小球向下运动到最低点时，物块M所受的拉力大小T．

在第(3)问中，必须用到在此位置沿绳方向加速度大小相等的结论，分析CA方向的小球受力，列出牛顿第二定律表达式T-mgcos53°=ma，才能求出物块所受的拉力．

小球在绕B点做圆周运动的过程中，相对与钉子A接触的绳上的A1点做圆周运动，小球相对A1点有切向和向心加速度，只有在最高点和最低点，小球的速度为0，相对A1点的向心加速度为0，沿绳方向的加速度相等．在教学中，如果不强调这个加速度关系成立的条件，直接使用这个结论，会让学生误认为在任何情况下沿绳方向的加速度都相等．在高考命题中应尽量避免考查绳杆模型的加速度关系，可考查其中的力和能量问题．

在教学中为了打破“沿绳方向的加速度相等”这个思维定势，可以通过分析一些实例来纠错，单摆模型就是一个很好的例子，固定的悬点没有加速度，在摆球运动过程中除了在最高点外都有向心加速度，所以沿绳方向加速度不一定相等．

5 结束语

本文通过分析一个绳牵连模型实例，阐述了绳转动时牵连物体的速度、加速度随位置、时间变化的规律，形象展现了相关物理量变化的图景，有助于纠正“沿绳方向的加速度都相等”、“往返运动中速度为0时一定有加速度”等错误认知．理论需要实验的检验，期待有研究者能减小摩擦阻力设计绳牵连模型的实验，利用Tracker等影像追踪分析软件研究实际运动规律，与理论分析结论进行印证．