畸形波作用下锚泊方柱系泊张力特性研究

潘文博，崔成，何萌，曾繁旭，梁晨，张宁川

( 1. 大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；2. 交通运输部天津水运工程科学研究院，天津300456)

1 引言

畸形波是一种广泛存在且具有突发性和能量集中性的异常大波。近年来，畸形波造成海上结构物及航行船舶安全事故的实例众多，通过大量海上观测得出畸形波广泛存在及非小概率事件的结论，促使工程及学术界对畸形波的研究越发关注。在畸形波生成机理、数值和物理模拟及其与结构物作用等方面的研究均已取得重要进展。迄今，畸形波的数值和物理再现技术日臻成熟。如Slunyaev 等[1]用非线性薛定谔（NLS）方程数值模拟畸形波。Clauss 等[2]基于一种改进的非线性方法在波浪水槽中生成“新年波”，再现“新年波”波面过程，并根据研究需要生成不同波高和波长的畸形波。Pei 等[3]用一个随机波列和两个瞬态波列叠加的方法，在实验室高效率定点生成畸形波。Cui 等[4]基于流体体积（VOF）方法建立完全非线性波浪数值模型，控制方程采用雷诺时均方程和k-ε方程，使用该模型模拟畸形波的生成、演化以及非平底地形对畸形波传播的影响。不同数值模拟方法在畸形波与结构物相互作用的适用性上，已有诸多讨论。如El Moctar 等[5]采用流体体积界面捕捉法来确定水和空气界面，结合计算流体动力学（CFD）和有限单元法（FEM），建立数值模型预测自升式钻井平台的畸形波载荷，与基于Morison 公式预测结果比较，基础剪切力和倾覆力矩两者预测差别不超过25%。Rudman和Cleary[6]成功地将光滑粒子（SPH）方法应用于畸形波和张力腿平台（TLP）相互作用研究，结果表明SPH方法可用于模拟波浪和结构物相互作用，可为波浪非线性提供一种有效的模拟方法。Zhao 等[7]基于固定笛卡尔网格系统的高阶有限差分法（CIP）模拟畸形波作用下浮式结构物的大幅度运动，并在二维水槽中进行试验以验证数模有效性。结果表明扭曲的自由水面（波浪破碎、水气混合等）和大振幅运动的数值结果与试验结果拟合效果很好，但波浪压力最大值与实际情况有些差异。Ning 等[8]提出了一种基于完全非线性势流理论的时域数值模型，研究了直立式防波堤在极端海浪下的性能，分析波谱带宽、直墙位置、波浪非线性等对垂直防波堤上海浪爬高和最大波浪荷载的影响。结果表明该数值模型能反映出主要的物理问题，尽管在预测波浪爬升时波浪压力方面存在一些差异，这可能是由于势流理论固有的假设，即目前的数值模型没有考虑涡流效应及波浪和垂直海堤之间的空气。

在畸形波与结构物相互作用方面，现有研究多见于时域方面的成果。Clauss 等[9]通过时域模拟和模型试验分析半潜式平台GVA4000 在畸形波作用下的运动响应和产生的冲击力，发现最大响应与畸形波波高直接相关，但运动响应的增加明显低于波高的增加。Schmittner[10]试验研究了畸形波作用下浮式生产储油船（FPSO）、大型起重船及半潜平台的运动和荷载响应。结果表明，考虑畸形波后各浮体结构的动力响应均大于规范和频域分析所预测的最大值。沈玉稿等[11]通过数值模拟结果，比较海洋平台在两种不同形式畸形波作用下的运动响应，分析了“孤立的”畸形波和“三姐妹”畸形波（连续出现3 个极大波浪）对平台运动的影响。结果表明，畸形波波峰是影响平台运动的主要参数，在平台设计时应主要考虑平台工作海域中极限波浪可能达到的最大峰值；在波峰值相同的条件下，平台运动的最大值随着畸形波的谱峰周期和有义波高的增加而增加；“三姐妹”波中的“邻波”对平台运动有一定的影响，随着“邻波”波高的增加，平台纵荡和垂荡都有所增加，但“邻波”对纵荡的影响相对较小。Deng 等[12]试验研究了畸形波、风和流与半潜平台之间的相互作用，讨论了系泊刚度的影响。结果表明，畸形波可能引起软系泊系统的大水平运动，并导致紧系泊系统的大系泊张力。Gao 等[13]数值模拟了指定畸形波序列与不同淹没深度水平圆柱的相互作用，结果表明畸形波会引起水平结构产生很大的垂向荷载，最大垂向载荷发生在畸形波接近抵达时刻。Pan 等[14]以相同试验频谱为出发点，基于模型试验，对比研究了畸形波和不规则波作用下，有限水深条件下系泊方柱的时域运动响应差异问题。定量地讨论了相对波高、相对周期与畸形波参数对系泊浮体运动时域响应的影响。本文在该工作的基础上，对比研究畸形波和不规则波作用下浮体系泊张力的差异，旨在明确不规则波浪序列中含有畸形波时浮体系泊张力特征的变化及其与畸形波参数的关系。采用小波方法计算畸形波和不规则波作用下浮体系泊张力的时频能量谱，研究它们的时频能量结构特点及畸形波参数对时频域能量分布的影响，为探讨畸形波对结构作用机理提供基础。

2 物理模型试验

2.1 实验设备和测试仪器

试验在大连理工大学海岸及近海工程国家重点实验室非线性波浪水槽中进行，该水池长60m、宽4m、深2.5m。造波机采用液压伺服不规则波造波系统，造波周期能力为0.5～5.0 s。水池尾部布置有多层消能设备，以尽量减少波浪的反射。

浮体运动量测量采用大连理工大学研制的浮式结构运动姿态光点摄像测量系统，采用双CCD 摄像记录光点的运动过程，基于配套软件获得刚性浮体6 个自由度运动分量。图像采集频率为50 Hz，位移量分辨率为10–4m 级，精度为10–3m 级；角度量分辨率为0.01°级，精度为0.1°级。锚绳拉力测量使用北京水利水电科学研究院研发的DYL-1A 型应变式水下拉力传感器。传感器线性度在0.999 以上，锚绳拉力测量精度为10–1N 级。波高测量采用北京水利水电科学研究院研发的DS30 型测量系统。该系统可配套64 点LG 型浪高传感器，同步采集波面过程并进行数据分析。LG 型浪高传感器的量程为50 cm，精度可达10–4m 级，标定线性度均在0.999 以上。

2.2 模型参数及布置

试验模型以中国海上某风电场锚地的3万t 级船舶锚泊结构为背景原型，其基本外轮廓为正方形柱体（边角为圆弧型），对系统进行适当简化，对应的模型截面边长D=50 cm，高h=62 cm，边角处为半径R=6.6 cm的圆弧，模型比尺为λ=35。浮体原型、模型的几何尺寸及水动力参数参见表1。

系泊缆绳原型采用直径75mm 尼龙材质缆绳，采用尼龙绳+弹簧+单位配重的形式来模拟，满足弹性（张力−相对伸长曲线满足相似条件）、长度和重量相似，锚泊采用四角八字方式。模型缆绳总长4m，系泊张力（Tm）和缆绳伸长量（Δs）满足

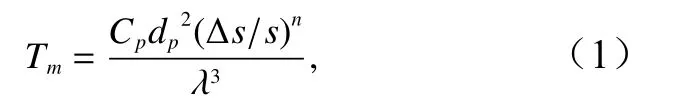
式中，Cp表示原型缆绳弹性系数，尼龙缆绳弹性系数可取Cp=1.540×104MPa；dp为原型缆绳直径（单位：m）；n为指数，尼龙缆绳指数取n=3。

基于系泊张力和缆绳伸长量满足弹性相似和重力相似，得到模型缆绳系泊张力与伸长量曲线如图1所示。

模型布置于畸形波生成指定位置，距离造波板21m。锚绳下端固定于水底，上端系泊点距模型底端25 cm 的圆弧中心位置，水下拉力计置于缆绳上端靠近模型系泊点位置。模型在水槽中的布置及模型系泊方式如图2 所示。

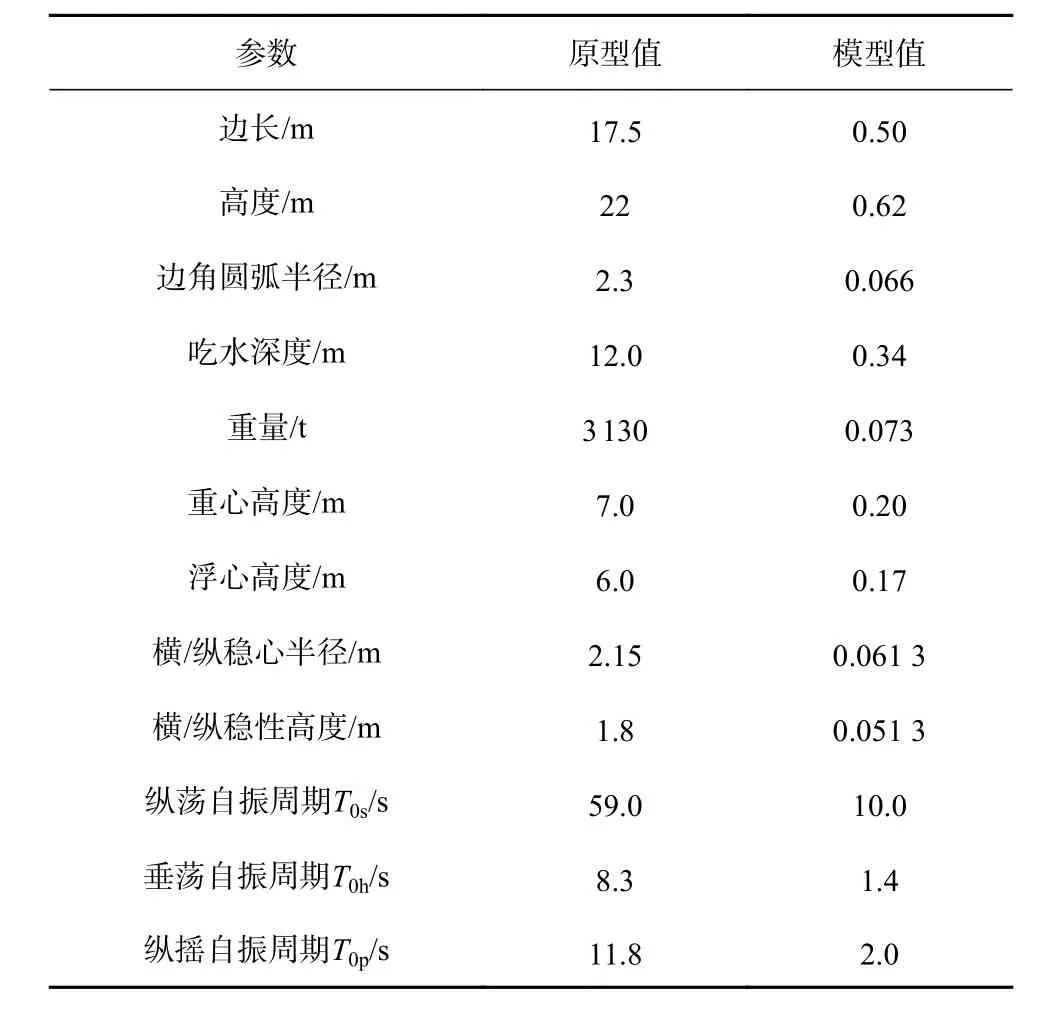
表1 浮体模型几何尺寸及水动力参数Table 1 Mechanical parameters of the rectangular cylinder

图1 系泊张力与缆绳伸长量关系曲线Fig. 1 Relationship ofmooring tension versus deformation

2.3 模型试验内容及方法

试验内容包括系泊浮体运动分量固有频率测试（静水衰减试验）、运动及系泊张力响应因子测试（规则波）、运动及系泊张力时间历程测试（畸形波和不规则波试验）4 部分，相关参数见表2。

影响系泊浮体动力响应因素主要包括浮体几何参数（边长D、高度h）、浮体水动力参数（表2）、波浪参数（有效波高Hs、最大波高Hmax、谱峰周期Tp、畸形波参数αn，αn包含4 项：α1=Hmax/Hs，α2=Hmax/Hmax−1，α3=Hmax/Hmax+1，α4=ηmax/Hmax。其中，Hmax−1和Hmax+1分别为最大波紧邻的前、后波波高，ηmax为最大波的波峰值）、系泊方式及缆绳初张力、水深等。本试验中将水深、浮体入水深度、系泊方式及缆绳初张力F0分别固定为：d=1.4m，h0=34 cm，F0=1.0～1.2 N。

在模型安装前，进行波要素率定试验，畸形波模拟采用三波列叠加方法[3]。试验测试了不同波浪条件下浮体运动响应和缆绳张力，本文只对缆绳张力展开讨论。对试验测定的参量进行时域统计分析和小波分析。时域统计分析获得各参量时间序列的最大值、1/10 大值、1/3 大值及平均值等统计特征值。采用小波分析方法计算畸形波和不规则波作用下浮体系泊张力时频能量谱，研究它们的时频能量结构特点及畸形波参数对时频域能量分布的影响。

2.4 小波分析方法

采用小波分析方法[15]计算浮体系泊张力时频能量谱，研究它们的时频能量结构特点和变化规律。将Morlet 小波函数作为小波变换的母函数，其解析式为

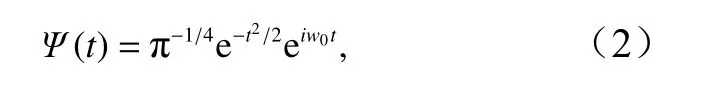
式中，t表示时间；w0表示无量纲频率，为了满足容许性条件，其值取为6。对离散序列xn的连续小波变换可写为

式中，*表示复共轭；s为小波尺度；n表示时间序列编号；δt表示时间间隔。

为了提高对离散序列的连续小波变换计算效率，根据卷积定理，小波变换可以写成傅里叶逆变换的表达形式为

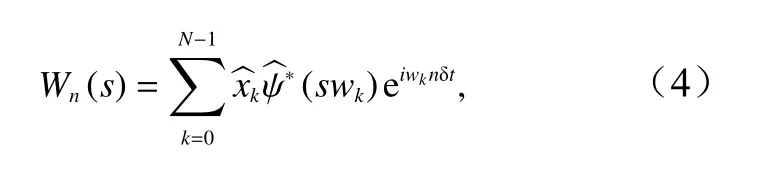
式中，k表示频率标号；δt表示时间间隔；(swk)表示傅里叶变换；wk为角频率，表示为

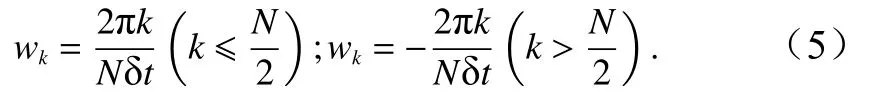
求解出小波变换系数，就可以定义小波能量谱的谱密度S(f,t)为

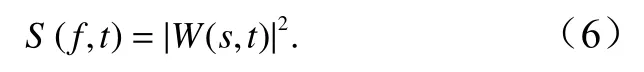
谱密度同时从时域和频域描述某物理参量的变化。对浮体系泊张力，可以刻画出畸形波（或最大波）发生时刻及其前后一定时段内，它们的时域和频域变化情况。为了定量研究这些变化，定义以下两个参数：

1）广义能量谱

对某物理量任意i时刻的时频谱，将其在频率内积分，其结果可类比地视为一种“广义能量谱”的时间变化过程，记为E（t），其时均值记为Etmean，计算公式为

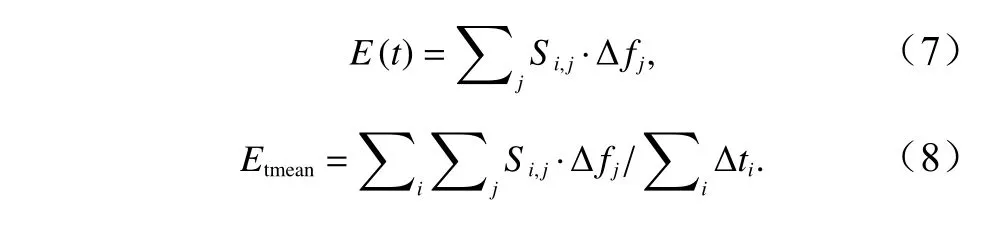
式中，小波谱S可同时表示时域和频域上能量分布情况；i表示任意时刻i；j表示任意频率j；Si,j表示任意i时刻j频率下的小波谱值。

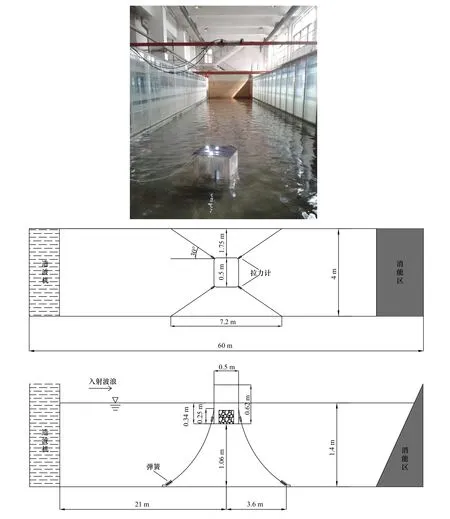
图2 模型系泊方式及在水槽中的布置Fig. 2 Mooring pattern and layout of themodel in the wave flumea. 模型布置实况；b. 平面布置图；c. 立面布置图a. Model placement; b. floor plan; c. elevation plan

在畸形波发生时刻（或不规则波序列中最大波时刻，t=c时刻）某物理量各频率成分的“广义”总能量记为Ec，即Ec=E（t）|t=c

表2 试验组别及相关参数Table 2 Summary of test groups and correlation parameters

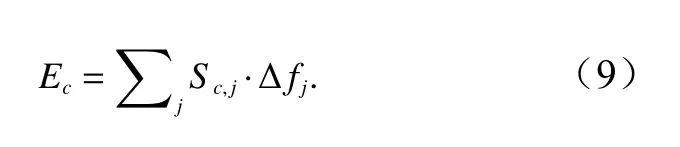
2）能量集中时域分布范围参数（ΔTE）

我们关注的是具有相同波浪频谱的两组不规则波序列作用时，浮体系泊张力差异问题。这两组不规则波序列，一组含有畸形波，另一组不含畸形波但有一个最大波。

不含畸形波序列作用下某响应的“广义能量谱”时间变化E（t）的最大值记为EImax；畸形波序列中，畸形波作用后，某响应的E（t）≥EImax起始时刻记为TEmin，E（t）≥EImax结束时刻记为TEmax，则畸形波响应时长ΔTE定义为

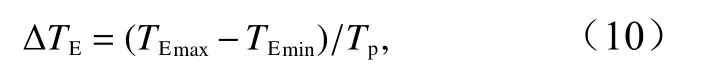
式中，Tp表示波浪谱峰周期，限定附加条件为TEmax～TEmin时段内均满足E（t）≥EImax。

显然畸形波响应时长ΔTE是一个无量纲的时间。物理含义上，畸形波响应时长ΔTE反映了畸形波发生后对某物理响应的“广义能量谱”超过不规则波序列中最大“广义能量谱”的持续时间。

3 试验结果分析

基于模型试验，讨论畸形波和不规则波作用下浮体系泊张力时频域特征随相对波高、相对周期和畸形波参数等因素的变化规律，采用小波方法计算畸形波和不规则波作用下浮体系泊张力时频能量谱，研究它们的时频能量结构特点及畸形波参数对时频域能量分布的影响。

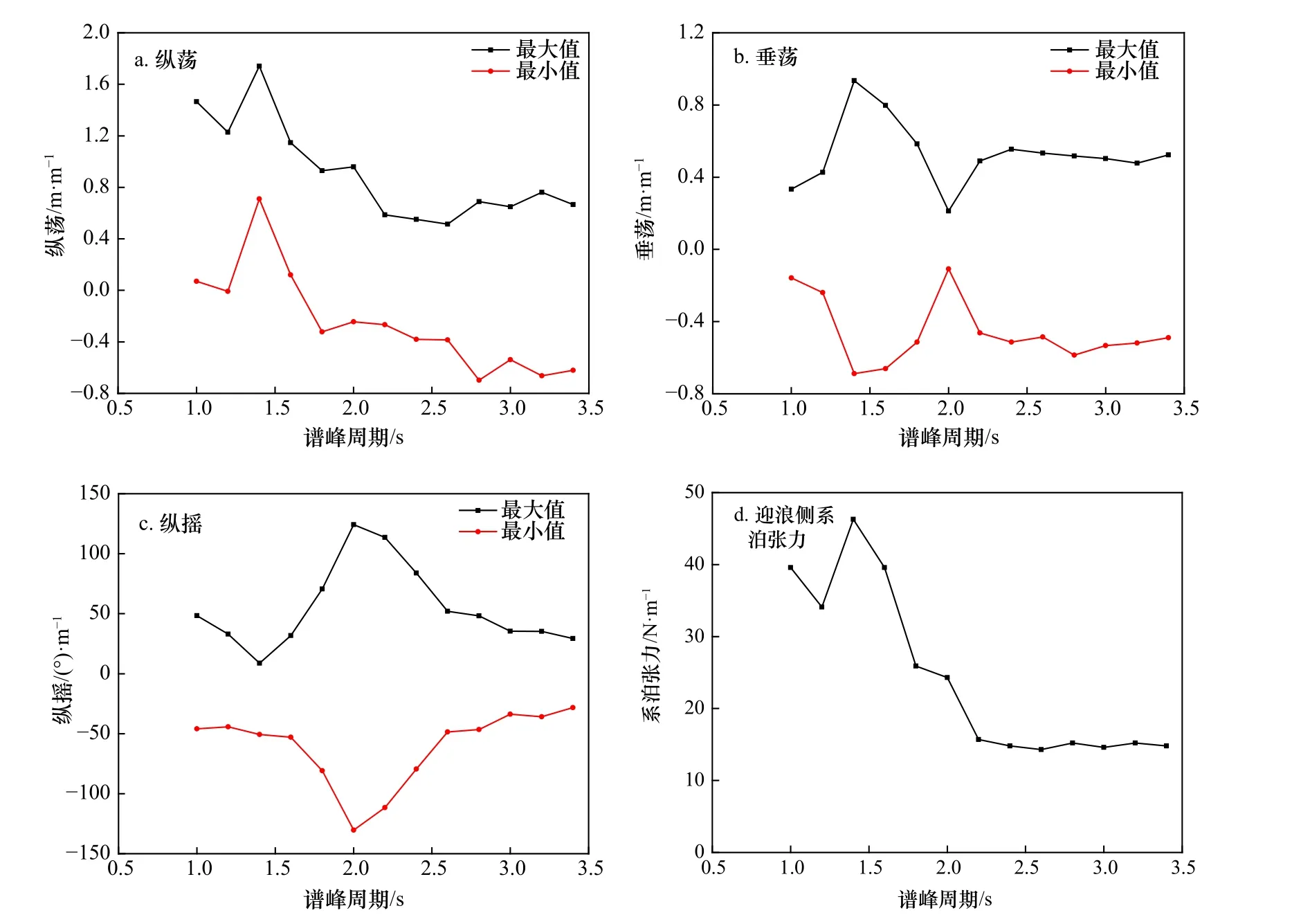
图3 浮体运动及迎浪侧系泊张力幅值响应算子试验结果Fig. 3 Response amplitude operators of themotion responses andmooring tension

3.1 静水衰减及RAO 试验结果

系泊浮体的固有周期是影响系泊系统动力响应的重要参数。基于静水衰减试验，得到系泊方柱的纵荡、垂荡和纵摇3 个运动分量固有周期分别为T0s=10.0 s，T0h=1.4 s，T0p=2.0 s。幅值响应算子（RAO）试验在规则波条件下进行，波高固定为H=10 cm，周期T=1.0～3.4 s，周期变化间隔为0.2 s。图3 给出了系泊方柱运动响应及迎浪侧系泊张力幅值响应算子随周期变化的试验结果（RAO 试验曲线）。由图3 可以看出，系泊方柱的垂荡和纵摇运动分别在各自的固有周期处产生各自的最大运动响应，且在正负方向上的幅值近似对称。受试验设备限制，试验周期范围未能达到纵荡运动固有周期，故该试验曲线并未能全面反映纵荡运动的RAO 特征。由纵荡运动RAO 曲线可以看出，纵荡在沿波浪传播方向的运动幅值大于负向幅值。在试验周期区间内纵荡运动最大值出现在Tp=1.4 s 附近，这可能是由于垂荡共振运动的耦合作用引起的。系泊浮体在小周期作用时产生较大的纵荡运动，Song 等[18]在扁平型沉管系泊试验中也阐释了该现象。Pinkster[19]将其解释为较小周期作用时，波浪的二阶平均漂移作用更为显著。浮体迎浪侧系泊张力RAO 曲线与浮体纵荡运动的幅值响应算子随周期变化的试验结果规律相同。

3.2 畸形波和不规则波波面及浮体系泊张力时间过程和频谱分析

选取两组不规则波，它们的有效波高Hs和谱峰周期Tp相同（Hs=8.0 cm，Tp=1.14 s），其中一组含有畸形波，畸形波参数为α1=2.0，α2=1.72，α3=2.03，α4=0.62；另一组为不含畸形波的常规不规则波，依然采用畸形波的4 个参数描述其中的最大波，其对应的值分别为α1=1.61，α2=1.40，α3=1.45，α4=0.61。

由于天然海浪具有随机性，相同的谱可对应无数个不规则波。同时这些样本中最大波高可能都是不同的。因此我们认为保证畸形波和不规则波的目标谱一致，其结果更有普遍性。图4 给出了畸形波和不规则波波面及对应的缆绳系泊张力历时曲线。由图4a 可以看到波列中显著存在的畸形波。由图4b和图4d 可以看出，两组波浪作用下，系泊张力均呈现出明显低于波浪频率的低频振荡特征，这是因为系泊系统中，纵荡运动是起控制作用的运动量。就两组波浪作用下系泊张力最大值而言，迎浪侧系泊张力在畸形波作用下显著大于不规则波作用，而背浪侧系泊张力在两组波浪作用下大小接近。由图4b 可以看出，畸形波作用下迎浪侧系泊张力显著增大后，出现背浪侧系泊张力大于迎浪侧的现象，这可能是由于畸形波出现后伴随着极深的波谷导致的[17]。

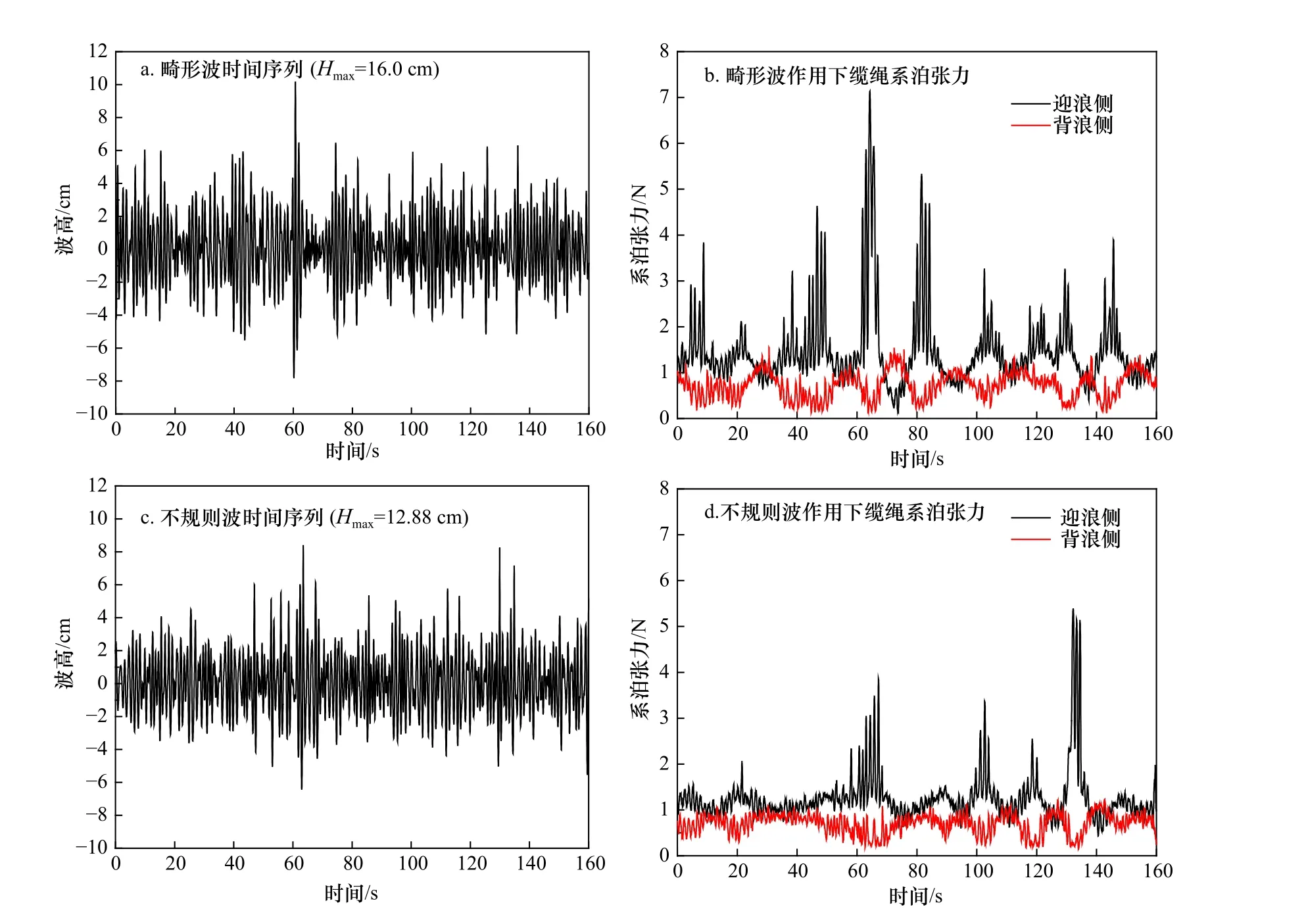
图4 缆绳系泊张力历时曲线（Hs=8.0 cm，Tp=1.14 s）Fig. 4 Time history ofmooring tension of the floater (Hs=8 cm, Tp=1.14 s)

3.3 系泊张力统计特征随相对波高变化对比分析

为考察相对波高变化时，畸形波和不规则波作用下浮体系泊张力规律及差异，选择一组相对波高变化的试验结果进行分析。在该试验序列中，波浪谱峰周期固定为Tp=1.4 s，有效波高和试验水深之比Hs/d=0.032～0.097。畸形波参数变化范围为：2.01<α1<2.20，1.71<α2<2.15，1.35<α3<2.13，0.53<α4<0.62；依然采用畸形波的4 个参数描述不规则波中的最大波，其对应值分别为1.51<α1<1.59，1.33<α2<1.69，1.92<α3<1.99，0.51<α4<0.63。通过时域统计分析，获得各个参数时间序列的最大值、1/10 大值、1/3 大值及平均值等统计特征值。图5 给出了畸形波和不规则波对应的迎浪侧系泊张力统计特征值随相对波高变化。图中横坐标以水深d为参量进行无量纲化。可以看出，无论是畸形波还是不规则波，迎浪侧系泊张力均随波高增大而增大，畸形波作用下系泊张力最大值明显大于不规则波作用，这与浮体纵荡运动结论一致[14]。统计迎浪侧系泊张力的1/10 大值、1/3 大值及平均值可见，畸形波和不规则波作用结果几乎一致。这说明畸形波对浮体迎浪侧系泊张力的影响限于畸形波发生的短时段内。

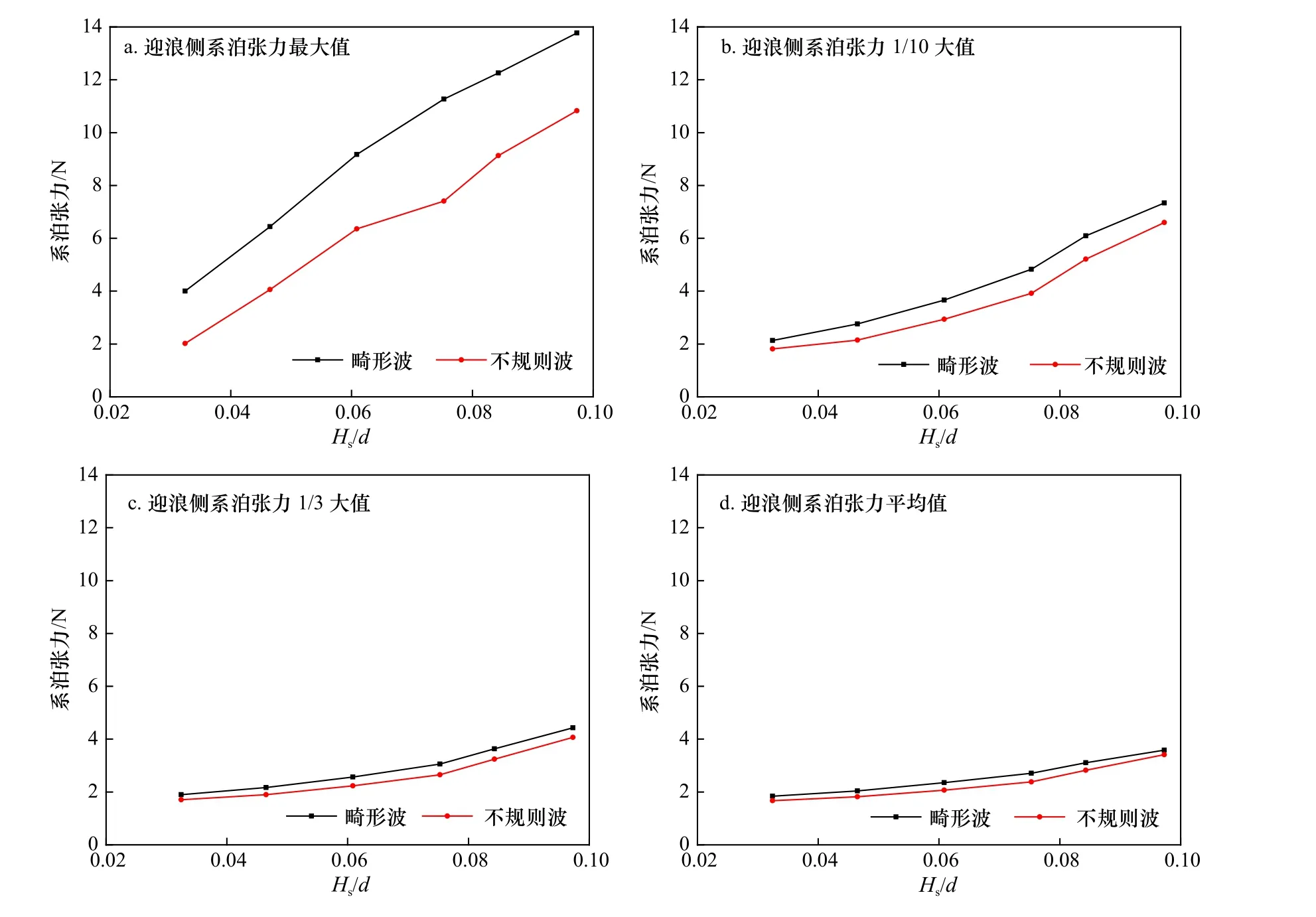
图5 畸形波和不规则波作用下缆绳迎浪侧系泊张力随相对波高变化比较（Hs/d=0.032～0.097，Tp=1.4 s）Fig. 5 Comparison of themooring tension varying with the relative wave height under the freak and random waves (Hs/d=0.032～0.097, Tp=1.4 s)

为进一步探究相对波高对浮体系泊张力的影响，图6 给出了两种波浪作用下迎浪侧系泊张力统计值比值随相对波高变化的试验结果。Fmax（f）/Fmax（i）、F1/10（f）/F1/10（i）、F1/3（f）/F1/3（i）和Faverage（f）/Faverage（i）分别表示畸形波与不规则波作用时，浮体迎浪侧系泊张力最大值、1/10 大值、1/3 大值及平均值之比。由图可见，在相对波高Hs/d=0.032～0.097 试验范围内，畸形波作用下迎浪侧系泊张力最大值比不规则波作用时增大27%～98%，1/10 大值比不规则波作用时增大11%～28%，1/3 大值比不规则波作用时增大8%～15%，平均值比不规则波作用时增大4%～14%。由图6 还可以看出畸形波与不规则波作用时，迎浪侧缆绳系泊张力的最大值之比随相对波高增大而减小，与浮体纵荡运动的变化趋势类似[14]。

3.4 系泊力统计特征随相对周期变化对比分析

为考察相对周期变化时，畸形波和不规则波作用下浮体系泊张力规律及差异，选择一组相对周期变化的试验结果进行分析。在该试验序列中，有效波高固定为Hs=8 cm，谱峰周期变化范围Tp=1.14～3.1 s，谱峰周期和浮体纵摇固有周期之比Tp/T0p=0.57～1.55，畸形波参数变化范围：2.01<α1<2.20，1.40<α2<2.14，1.40<α3<2.37，0.51<α4<0.66；依然采用畸形波的4 个参数描述不规则波中的最大波，其对应的值分别为1.45<α1<1.53，1.06<α2<2.16，1.29<α3<1.99，0.51<α4<0.64。

图7 给出了畸形波和不规则波作用下迎浪侧系泊张力统计特征值随相对周期变化。可以看出，无论是畸形波还是不规则波，迎浪侧系泊张力随周期的变化规律基本相同，且与RAO 试验结果一致，系泊浮体在较小周期作用时产生较大的系泊张力，然后迎浪侧系泊力随相对周期的增大而减小，这是因为较小周期作用时，波浪的二阶平均漂移作用更为显著。在相对周期Tp/T0p=0.57～0.92（Tp/T0h=0.81～1.31）范围内，系泊张力随周期增大呈振荡性变化并出现最大值，这可能是因为波浪谱峰周期与垂荡固有周期接近，各个运动量之间的耦合作用引起的[16]。在相对周期Tp/T0p<1时，畸形波作用下系泊张力显著大于不规则波作用，在相对周期Tp/T0p>1 时，随相对周期的增大，畸形波作用下系泊张力逐渐接近不规则波的作用，两者基本一致。由图7 还可以看出在相对周期Tp/T0p<1 时，迎浪侧系泊张力明显大于背浪侧，这是因为平均漂移力的影响，纵荡运动的平均值有所漂移的缘故。当在相对周期Tp/T0p>1 时，迎浪侧和背浪侧系泊张力最大值差距随波浪相对周期增大而减小，甚至出现背浪侧系泊张力大于迎浪侧现象，这可能是因为长周期波浪的浅水效应，波峰变陡和波谷变平变长，对应纵荡运动平均漂移值为负，且随着相对周期增加，背浪侧系泊张力几乎保持不变，畸形波和不规则波对应的背浪侧系泊张力几乎一致。

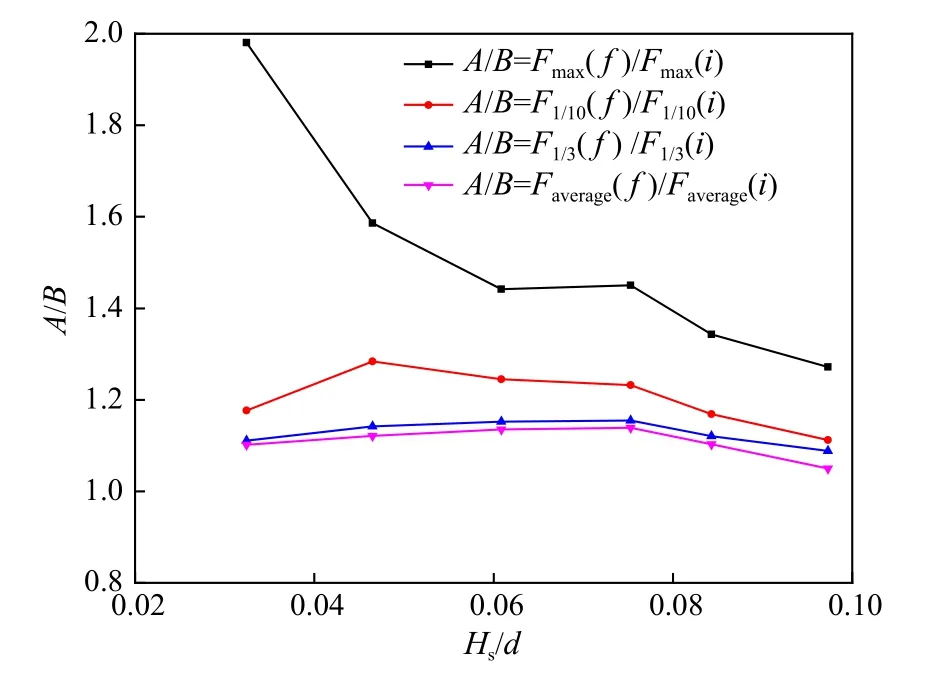
图6 系泊张力统计特征值比值随相对波高变化（Hs/d=0.032～0.097，Tp=1.4 s）Fig. 6 The variation of statistical characteristics ofmooring tension versus the relative wave height(Hs/d=0.032～0.097, Tp=1.4 s)Fmax(f)/Fmax(i)、F1/10(f)/F1/10(i)、F1/3(f)/F1/3(i)和Faverage(f)/Faverage(i)分别表示畸形波与不规则波作用时，浮体迎浪侧系泊张力最大值、1/10 大值、1/3 大值及平均值之比Fmax(f)/Fmax(i), F1/10(f)/F1/10(i), F1/3(f)/F1/3(i), and Faverage(f)/Faverage(i) are the ratio of themaximum value, 1/10 value, 1/3 value and the average value of themooring tension under freak and random waves

为了定量比较相对周期对浮体迎浪侧系泊张力的影响，图8 给出试验范围内，两种波浪作用下迎浪侧系泊张力比值随相对周期变化试验结果。由图可以看出畸形波和不规则波作用下浮体迎浪侧系泊张力最大差别出现在相对周期Tp/T0p<1 范围内，在该区畸形波比不规则波作用下的迎浪侧系泊张力约增大22%～39%。

3.5 系泊张力统计特征随畸形波参数α1 变化对比分析

为考察畸形波参数α1对浮体系泊张力影响，选择一组α1变化的试验序列（α1=1.91～2.83）结果进行分析。该试验序列中，固定有效波高和谱峰周期（Hs=8 cm，Tp=1.6 s），畸形波其他3 个参数变化范围为：α2=1.30～1.52；α3=1.42～1.60；α4=0.51～0.56。图9 给出浮体迎浪侧和背浪侧系泊张力最大值随畸形波参数α1变化试验结果。图中同时还给出3 组不规则波的试验结果。对不规则波中的最大波，依然采用畸形波的4 个参数描述，其对应值分别为：1.57<α1<1.60，2.15<α2<2.31，1.92<α3<1.99，0.54<α4<0.55。

由图9a 可以看出，浮体迎浪侧系泊张力和畸形波参数α1显著相关，随α1的增大而增大（接近线性增长），在α1=1.91～2.83 范围内，畸形波作用下迎浪侧系泊张力可达不规则波作用时的1.32～1.90 倍。图9b显示，当畸形波参数α1>2.0 时，背浪侧系泊张力随畸形波参数α1的增大而适当增大，可达不规则波作用时的1.03～1.66 倍，这可能是因为畸形波发生前和发生后对应于较大波峰的是较大波谷[17]。

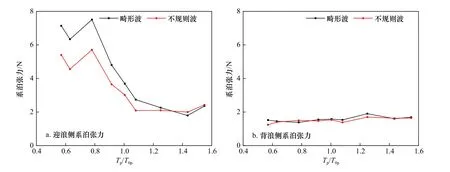
图7 畸形波和不规则波作用下缆绳系泊张力随相对周期变化（Hs=8 cm，Tp/T0p=0.57～1.55）Fig. 7 Comparison of themooring tension varying with the relative period under the freak and random waves (Hs=8 cm, Tp/T0p=0.57～1.55)

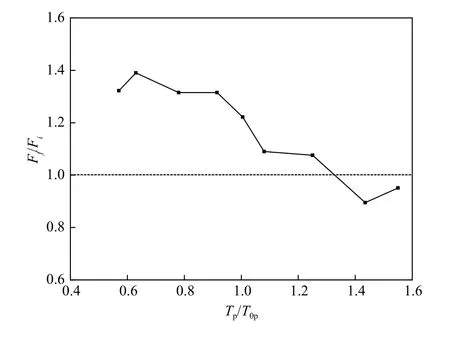
图8 迎浪侧系泊张力最大值比值随相对周期变化（Hs=8 cm，Tp/T0p=0.57～1.55）Fig. 8 The variation of statistical characteristics ofmooring tension versus the relative period (Hs=8 cm, Tp/T0p=0.57～1.55)Ff /Fi 表示畸形波与不规则波作用时，浮体迎浪侧系泊张力最大值比值Ff /Fi represents the ratio of themaximummooring tension on the windward side of the floating body under the freak and random waves

3.6 系泊张力时频谱和广义能量谱分析

上述分析可以看出，畸形波作用下浮体系泊张力显著大于不规则波的作用结果。为进一步分析两种波浪作用下浮体系泊张力的异同，采用小波分析方法计算系泊张力的时频能量谱，研究它们的时频能量结构特点及畸形波参数对时频域能量分布的影响。图10给出了基于小波分析方法得到的相同波谱条件下，畸形波和不规则波作用时，浮体迎浪侧系泊张力时频谱计算结果示例。由图可见，两种波浪作用下浮体系泊张力时频谱有所不同。畸形波作用下系泊张力时频谱显著增大。目前畸形波作用下时频谱大值出现的时、频范围及特征尚无研究，在此引入“广义能量谱”E（t）来描述。图11 给出畸形波和不规则波作用时，浮体系泊张力广义能量谱计算结果示例。由图可见，畸形波和不规则波作用下系泊张力的广义能量谱显著不同，且随着畸形波参数α1的增大，畸形波响应时长ΔTE有增大趋势。

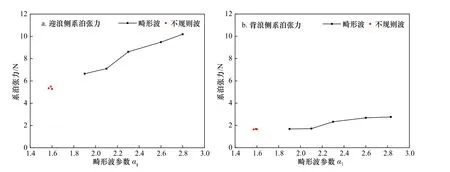
图9 畸形波和不规则波作用下系泊张力随畸形波参数α1 变化（Hs=8 cm，Tp=1.6 s）Fig. 9 Comparison of themooring tension varying with α1 under freak and random waves (Hs=8 cm, Tp=1.6 s)

4 结论

（1）相同频谱条件下畸形波和不规则波对系泊方柱作用，系泊张力最大值有相当大的差别，该差别与相对波高、相对周期有关，同时与畸形波参数α1显著相关，但系泊张力的1/3 值和平均值则无工程意义的不同。

（2）在相对波高Hs/d=0.032～0.097 试验范围内，畸形波作用下迎浪侧系泊张力最大值比不规则波作用约增大27%～98%，1/10 大值约增大11%～28%，1/3 大值约增大8%～15%，平均值约增大4%～14%。畸形波与不规则波作用时，迎浪侧系泊张力最大值之比随波高增大而减小。

（3）在相对周期Tp/T0p=0.57～1.55 试验范围内，畸形波和不规则波作用下迎浪侧系泊张力随周期变化规律基本相同，且与浮体纵荡运动规律相同。在相对周期Tp/T0p=0.57～0.92（Tp/T0h=0.81～1.31）范围内产生较大的系泊张力，该范围内系泊张力随周期增大呈振荡性变化并出现最大值，此后随相对周期增大而减小。在相对周期Tp/T0p<1 时，畸形波作用下系泊张力显著大于不规则波作用，约增大22%～39%。在相对周期Tp/T0p>1 时，随相对周期增大，畸形波作用下系泊张力逐渐接近不规则波的作用，两者基本一致。

（4）畸形波参数α1和迎浪侧、背浪侧系泊张力显著相关。在α1=1.91～2.83 试验范围内，畸形波作用下迎浪侧和背浪侧系泊张力最大值可达不规则波作用的1.32～1.90 倍和1.03～1.66 倍。

（5）采用小波分析方法，讨论系泊浮体系泊张力特征是一个有效的方法。该方法与统计分析和谱分析方法比较，更能有效地描述畸形波作用时浮体动力响应特征，同时更能清晰地区分畸形波和不规则波作用下的差异。畸形波和不规则波作用比较，浮体系泊张力的广义能量谱E（t）和能量集中时域分布范围参数ΔTE有显著的差别。

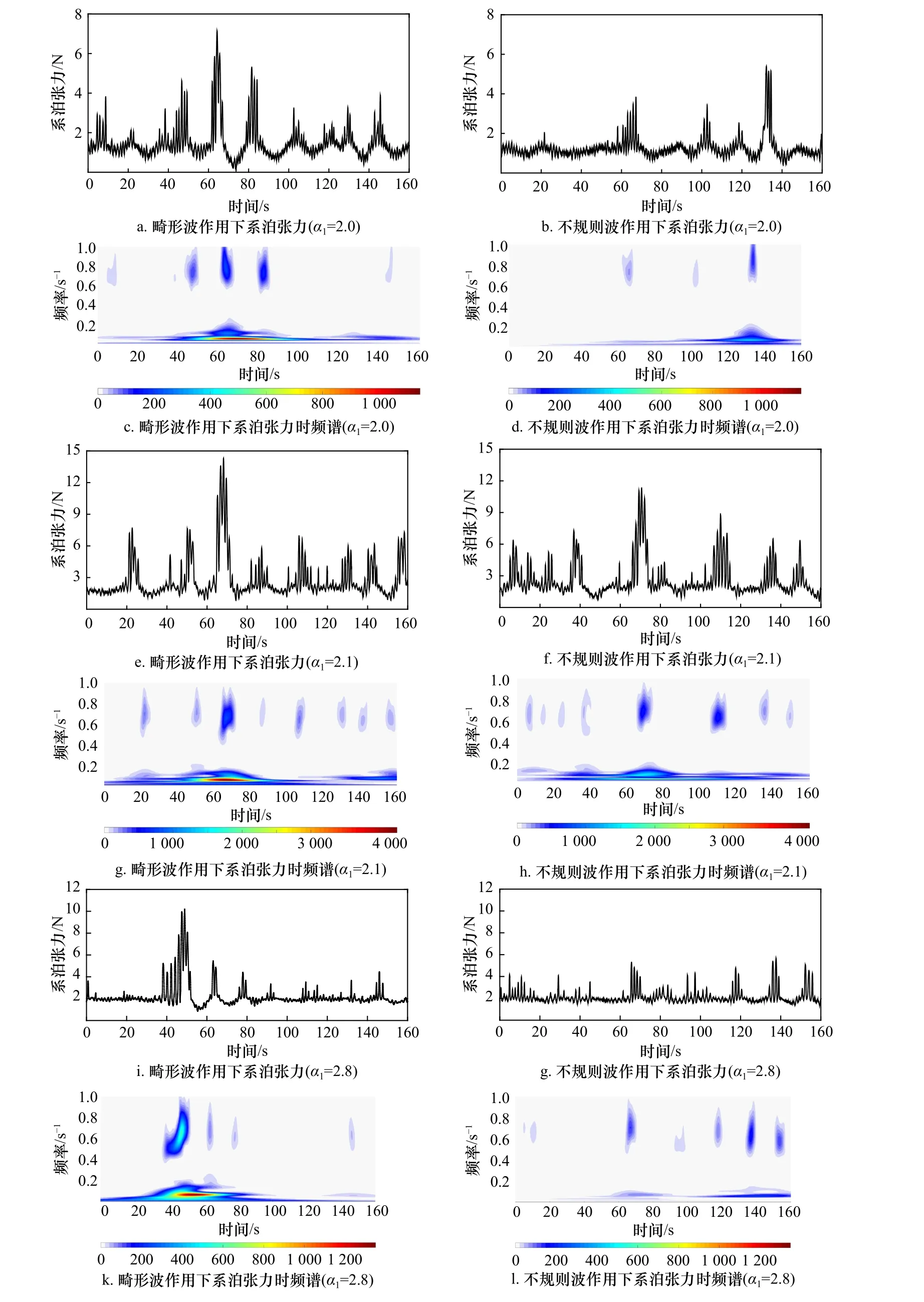
图10 不同波高和周期条件畸形波和不规则波作用下缆绳系泊张力时频谱对比Fig. 10 Time-frequency spectra ofmooring tension under the freak and random waves of different conditionsa−d. Hs=8.0 cm, Tp=1.14 s; e−h. Hs=13.6 cm, Tp=1.4 s; i−l. Hs=8.0 cm, Tp=1.4 s

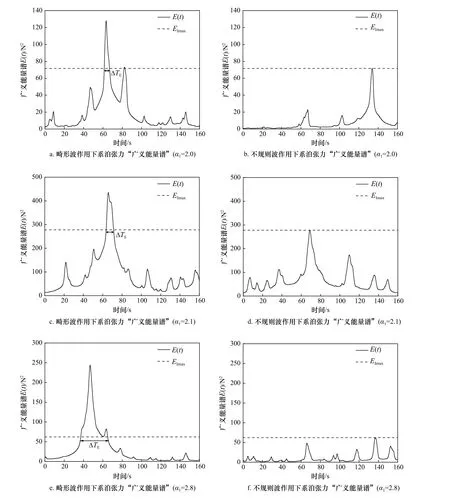
图11 不同波高和周期条件下畸形波和不规则波作用下系泊张力“广义能量谱”E(t)对比Fig. 11 Generalized energy spectrum ofmooring tension under the freak and random waves of different conditionsa, b. Hs=8.0 cm, Tp=1.14 s; c, d. Hs=13.6 cm, Tp=1.4 s; e, f. Hs=8.0 cm, Tp=1.4