海底地形对洋中脊热液对流活动的影响研究<br/>——基于海水压力的空间变化

海底地形对洋中脊热液对流活动的影响研究
——基于海水压力的空间变化

2020-10-09范庆凯李江海

海洋学报 2020年9期

范庆凯，李江海*

( 1. 北京大学地球与空间科学学院造山带与地壳演化教育部重点实验室，北京 100871；2. 北京大学石油与天然气研究中心，北京 100871)

1 引言

洋中脊热液对流循环是地壳热量输出的主要方式，通过这种方式输出的总热量大致可占全球地壳热输出的25%[1]，也是新生洋壳产生和地球化学循环的主要影响因素[2–3]。在洋中脊扩张中心，海水沿洋壳内的断裂−裂隙系统向下渗透至岩浆侵入体附近，在岩浆熔体等热源的加热和驱动下与围岩发生热化学反应并逐渐汇集上涌，形成富集的热液矿体。

前人研究结果表明，影响洋中脊热液对流系统的因素包括洋壳渗透率结构、热源位置与温度，以及洋壳增生模式等[4–9]。洋壳内部热液对流的形态直接取决于各方向的流体压力梯度，热液流体倾向于沿高流体压力梯度向低压区汇集、喷发。洋底地形起伏引发的下伏洋壳流体压力梯度变化也导致了热液喷发活动多发育于洋底高地形[10]。发育于快速和慢速扩张洋中脊的多个热液区（如东太平洋海隆（EPR）9°17′N 热液区和大西洋洋中脊Lucky Strike 热液区）直接证明了海底地形对其下伏热液对流系统的影响。相关的解析模型和数值模拟研究表明洋底高地形对热液上涌和喷发的汇聚作用[11–13]。

然而，除了引起下伏洋壳内部流体压力梯度的变化之外，洋底地形起伏相关的水深变化也直接导致了洋底上覆海水压力的变化，即高地形上覆压力较低，低地形则较高。这种海水压力的空间变化是否会对洋壳内部热液对流形态产生影响，从而导致其沿高地形汇聚、喷发仍不得而知。本文主要从这一方面入手，通过基于弹性孔隙模型的数值模拟，主要聚焦于洋底地形起伏引起的上覆压力跨轴变化对下伏热液对流系统的形态和热液喷发位置的影响，即基于洋底上覆压力的单因素研究。旨在探索一个可以定量描述海底高地形和热液对流系统的横向偏移程度之间关系的实验模型，并结合实际观测[14–18]，对比不同类型洋中脊的热液活动。

2 研究方法与数据来源

本文应用基于弹性孔隙模型的有限体积模型，基于Matlab 计算平台运行。该模型通过孔隙介质中达西流体的运动规律来模拟洋壳内部实际的热液对流活动，具体的模拟方法与文献[19]相似，但采用不同的初始、边界条件，来探讨海水压力的空间变化这一单因素的影响。另外，我们选择EPR 9°17′N 热液区和Lucky Strike 热液区作为对比实例，主要因为：（1）两个研究区分别属于快速扩张洋中脊和慢速扩张洋中脊，从而更具全面性；（2）二者皆发育有不同规模的高温热液活动（前者喷发温度约388℃，后者约333℃，引自Interridge 数据库[20]），且均喷发于洋底高地形；（3）在二者下伏洋壳内均发现了可维持热液对流活动的地震波速异常[14,17]，从而可以直观、合理地对比热源的位置和规模。其中，EPR 9°17′N 热液区和Lucky Strike 热液区的跨轴地形数据均引自海洋地学数据库系统（MGDS, http://www.marine-geo.org/portals/gmrt/[21]）。

3 热力学数值模拟

3.1 控制方程

本文的数值模型通过应用基于布辛涅司克近似定义（Boussinesq Approximation）[19,22]的达西定律来解孔隙介质中的流体和热量传导方程，以获得不同时间的流体速度和温度。在这种基本框架内，模型中流体的质量守恒定律可以表述为

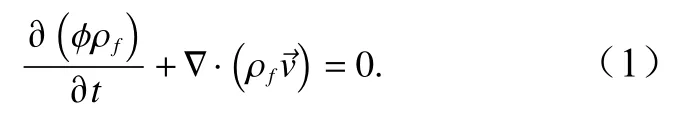
方程（1）对应基于单相流体充填、各向均一介质的对流模型。式中，ρf为流体密度；ϕ为模型基质孔隙度；为达西流体速度，可通过达西定律直接获得，即

孔隙介质热传递方程[23]可表述为

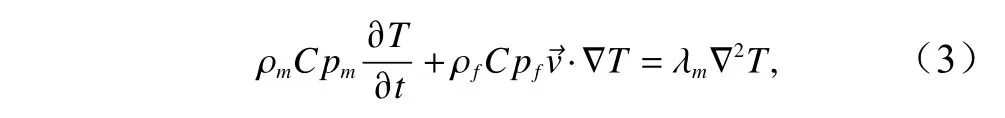
式中，T为温度；t为时间；ρm和Cpm分别代表流体−围岩混合体的密度和比热容；Cpf为流体比热容；λm为流体−围岩混合体的热传导系数。上覆箭头则代表矢量参数。

关于流体参数，本文应用温度、压力相关的非线性流体性质（密度、黏度、比热容等[24–26]）。而基于简化的线性流体方程，流体密度可视为温度的线性函数，即

式中，ρf0和T0分别表示海水的密度和温度；α为热扩张系数；T为洋壳内部流体温度。

在洋壳内部热传导的背景下，当热液流体的达西速率远大于热传导速度时，洋壳内部明显的热液对流循环得以发生，二者的比值即为瑞丽数（Ra），即

式中，αf为流体热扩张系数；κm为流体−围岩混合体热扩散系数；υf为流体的运动学黏度；TH为热源温度；H为模型高度；λm为热传导系数。当瑞丽数大于特定的临界值（Rac）时，热液对流最终产生，该临界值会随着模型的形状、参数等变化，具体数值可由实验获得。另外，瑞丽数的大小直接与热液对流系统的强度呈正相关关系，瑞丽数越大，热液对流越剧烈，反之则越微弱[9,27]。

热传导的输出功率（QC）可由海底热扩散温度与下伏热源温度差、模型高度等参数获得，即

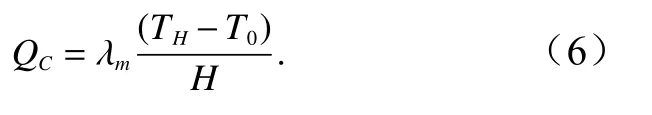
洋底的总热量输出（Q）通常表现为洋壳内部热对流与热传导功率的总和，与热传导输出量的比值称为纳赛尔数（Nu>1），即

Nu与热液对流系统的Ra表现为线性相关（ζ～0.1）：

因此，可最终获得洋中脊总热量输出功率为

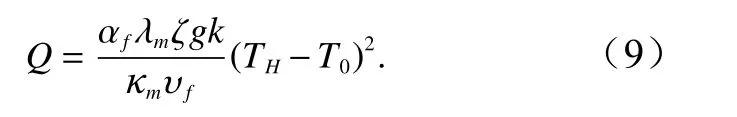
3.2 模型设置与边界条件

本文应用的模型为长方形块体，代表洋中脊轴向或离轴一定距离（l=20km）和深度（h=10km）的剖面（图1）。模型主体为具有固定孔隙度（3%）的渗透层[22]，代表以喷发性玄武岩为主的洋壳。上界为海底面，设置为对流体开放的边界，并赋予固定（20 MPa）或变化的上覆压力和温度（0℃），代表固定或变化的海水深度和海底地形起伏。模型的边界和底界均被设置为绝热、封闭的边界。

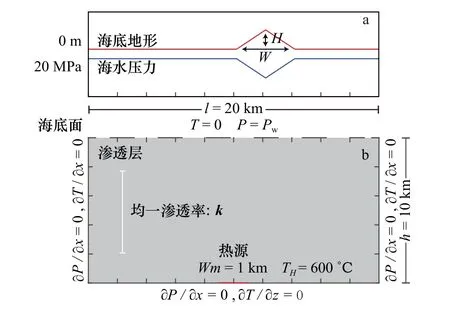
图1 模型设置与边界条件Fig. 1 Model setup and boundary conditionsa. 上覆压力分布与其所代表的海底地形起伏示意图;b. 模型尺寸与边界条件a. Schematic sketch for the distribution of overlying pressure and bathymetric relief; b.model size and boundary conditions

为了研究洋壳上覆海水压力的单因素影响，排除包括难以预测的洋壳渗透率结构[28–29]和洋壳增生方式对洋壳内部热液对流形态的潜在影响，并鉴于模型运行的时间成本，本文赋予模型各向均一分布的渗透率值（k=1×10−15m2）。依据前人研究结果[30]，高于600℃的洋壳层位可被视为非渗透层，且在发育有稳定岩浆透镜体的快速−中速扩张洋中脊，其透镜体的宽度均在1km 左右[31–32]。基于上述原因，我们将固定温度（600℃）、固定宽度（1km）的高温区域设置于模型底界的中心位置，代表驱动、维持上覆热液对流循环的热源。海底上覆压力的变化及其代表的海底地形起伏作为数值模拟的唯一变量，主要通过设置一定高度（H）和宽度（W），且两侧固定的高地形（图1a）来实现，高地形之外统一设置为平坦地形。与洋底地形相关的海水深度直接决定了海底上覆压力的分布（图1a）。其中，高地形高度值分布范围为5～150m，宽度则分别为2000m、4000m、6000m 和8000m，且高地形左侧起点与热源中心位置保持在相同的水平位置（图1b）。

为了研究稳态下热液喷发位置和地形高点间的关系，我们将各模型分别运行至1～10 Ma 不等，以确保其全部达到稳态。

4 研究结果

4.1 数值模拟结果

经过模拟不同规模高地形引发的海底上覆海水压力变化对其下伏热液对流系统形态的影响，本文最终获得约120 组稳态数值模拟结果（海底高地形起伏值5～150m，以5m 为间隔，高地形起伏宽度值分别为2000m、4000m、6000m 和8000m）。基于数值模拟结果，不同规模的地形起伏会使下伏热液系统产生不同程度的横向偏移，最终致使洋壳内部热液羽向海水压力低值点（地形高点）汇集。

综合所有模拟结果，洋壳内部上升热液羽表现为大致相同的宽度（约3km）和相似的热液喷发温度（约250℃）以及热流输出功率。当海水压力低值为19.5 MPa（对应地形高度约50m），压力低异常区宽度为约2km 时（图2a），下伏高温热液羽表现为一定程度地向海底低压区转移的现象，具体表现为偏离原始热源位置约800m（图2b）。保持海底低压区的规模不变，将其谷值减小至19 MPa（图2c，对应100m 的地形高度），洋壳内部热液羽则表现为明显的偏移，完全汇聚并喷发于海水压力低值点（地形高点，图2d）。

将地形起伏区增加至4km 宽，最大高度保持为50m（图2e），洋壳内部热液羽表现为偏离热源位置约1700m，并向海底压力低值区（高地形点）转移的特征（图2f）。相似地，在地形起伏规模不变的基础上，进一步减小地形高点的海底压力极值（至约19 MPa，对应100m 高的地形高点，图2g），洋壳内部热液对流系统则表现为完全程度的偏离和汇聚效应，即海底热液喷发位置完全与海底高地形点重合（图2h）。

综合上述现象，并结合所有的模拟输出结果（图3），海底地形起伏的横向宽度和纵向高度均会对洋壳内部热液对流系统的形态产生不同程度的偏移影响，具体表现为海底高地形规模和地形起伏程度的增加均会明显提升其对洋壳内部热液对流系统的偏移影响。在特定海底高地形宽度的情况下，洋壳内部上升热液羽会在某一特定临界高度值形成完全程度的偏移效果，即海底热液喷发完全集中于地形高点的位置（图3a），并且此临界值表现为随海底高地形宽度的增加而增加的趋势。同理，洋壳内部热液羽的横向偏移角度可根据相应的偏移距离得出（图3b），并表现出类似的规律。

4.2 解析模型

依据模拟得出的洋壳内部热液羽偏移距离和偏移角度的统计结果（图3），我们可以通过一定的统计学规律来获得可以定量描述海底地形起伏（海底上覆压力变化）与洋壳内部热液羽偏移程度以及热液喷发位置的解析模型，

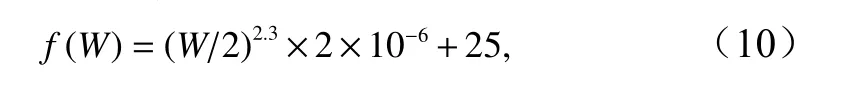
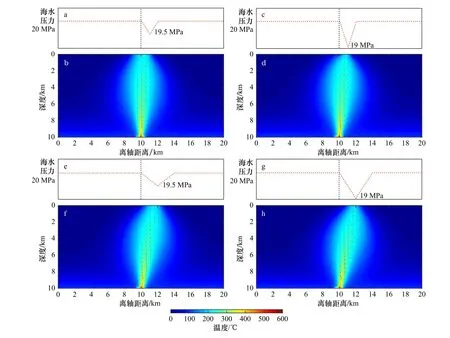
图2 数值模拟结果Fig. 2 Simulation resultsa. 2000m×50m 高地形数值模拟结果; b. 2000m×100m 高地形数值模拟结果; c. 4000m×50m 高地形数值模拟结果; d. 4000m×100m高地形数值模拟结果a. Simulation with a bathymetric high of 2000m×50m; b. simulation with a bathymetric high of 2000m×100m; c. simulation with a bathymetric high of 4000m×50m; d. simulation with a bathymetric high of 4000m×100m

式中，W为海底高地形起伏的宽度；H为海底高地形起伏极值的高度；D表示洋壳内部热液羽的偏移距离。

依据获得的基于统计学的解析模型，洋壳内部热液羽向高地形的偏移距离（图4a）和偏移角度（图4b）均由海底高地形的规模决定。基于该模型（图4），洋壳内部热液羽的偏移程度表现为最大偏移距离约5km 和最大偏移角度约26°，二者均表现为海底高地形起伏的宽度和高度的函数，且海底地形越高，规模越大，下伏热液羽向高地形的偏移程度就越大，符合上述模拟结果（图2）。

5 讨论

上述数值模拟结果表明海底上覆海水压力的不均一分布会最终导致洋壳内部热液对流系统向海底高地形区域汇集并喷发，这也符合前人的研究结果[11–13]。本节主要聚焦于现今仍在活动的洋中脊热液系统，应用热液系统相关的实际海底地形剖面和已知的岩浆热源尺寸与位置，来探究实际的海底地形对热液对流系统的偏移影响。

5.1 EPR 9°17′N 热液区热液活动

东太平洋海隆是典型的快速扩张洋中脊（全扩张速率约110～150mm/a[33]，EPR 9°17′N 及其相邻区域表现为相对平缓的跨轴地形变化和洋脊轴处相对较高的地形[18,34–35]（图5a），并在下伏约1.5km 的深度发育连续的透镜状岩浆熔融体[3]，EPR 9°17′N 热液区即为发育于该研究区轴部高地形[15]（图5a）的高温热液活动区（约388℃, 引自Interridge 数据库[20]）。依据研究区跨轴水深分布，我们计算出研究区跨轴海水压力剖面（图5b），并将其设置为模型上界的压力边界条件。

基于EPR 9°17′N 热液活动区的实际情况（包括上覆海水压力的跨轴变化和下伏岩浆热源的规模、位置），我们将模型设置为10km×3km，代表10km 的跨轴距离和3km 的洋壳厚度，高温（约600℃，宽度约为2km）热源位于模型底界中央，代表EPR 9°17′N热液活动区下伏的连续性岩浆透镜体（图5c），同时将模型渗透率设置为均一值（约11×10−15m2）。运行该模型至 100 ka，确保其到达稳定状态。

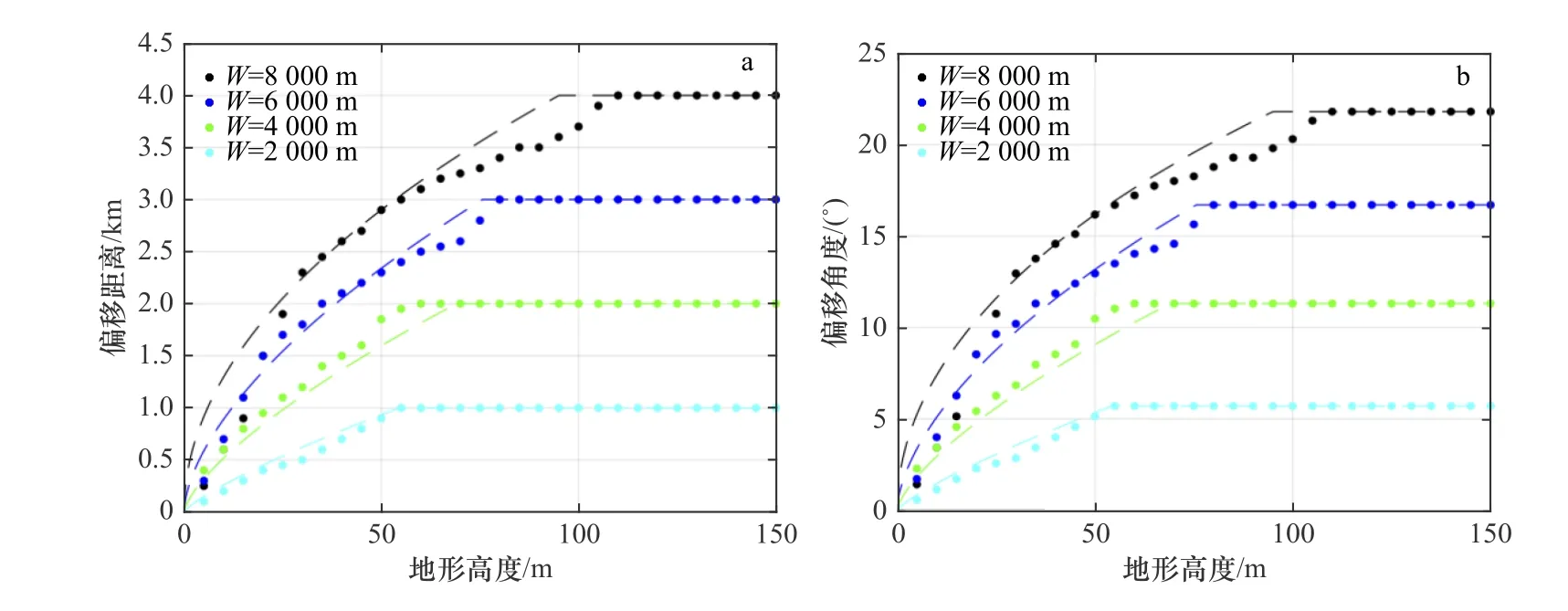
图3 热液羽偏移程度与地形高度的关系Fig. 3 Relationship between deviation of fluid plumes and height of bathymetric highsa. 热液羽偏移距离与地形高度的关系; b. 热液羽偏移角度与地形高度的关系a. Relationship between deviation distance of plumes and height of bathymetric highs; b. relationship between deviation degree of plumes and height of bathymetric highs

图4 热液羽偏移程度实验模型Fig. 4 Experimentalmodel of the deviation of plumesa. 热液羽偏移距离实验模型; b. 热液羽偏移角度实验模型a. Model of the deviation distance of plumes; b.model of the deviation degree of plumes

依据稳态数值模拟结果（图5c），EPR 9°17′N 下伏洋壳发育约1km 宽的高温（约330℃）热液羽，并离轴向洋脊轴高地形偏移约1km 的水平距离，最终的热液喷发位置与实际的EPR 9°17′N 热液区位置（图5a）保持高度一致，表明这一模型较好地展示了高地形对实际热液活动喷发位置的影响。

5.2 大西洋Lucky Strike 热液区

Lucky Strike 热液区位于慢速扩张（全扩张速率约为21mm/a[36]）的大西洋洋中脊37°17′N，是全球范围内最大规模的热液循环系统之一。受到其北东方向Azores 热点的影响[37]，该热液区范围内发育大量玄武质熔岩[38]和明显的高地形起伏，Lucky Strike 热液区便位于区内较高的地形上（图6a）。文献[17]通过地震反射波速异常揭示了在Lucky Strike 热液区下伏3km 的深度范围内发育约4km 宽的透镜状岩浆部分熔融体，可认为其为维持上覆Lucky Strike 热液对流系统运行的岩浆热源。

基于Lucky Strike 热液区的实际情况，我们将模型设置为10km×3km，高温热源（600℃，宽约4km）位于模型底界中央，对应实际的岩浆部分熔融体[17]。通过研究区跨轴水深分布计算得出对应的跨轴海水压力剖面（图6b），并将其设置为模型顶界的压力边界条件，其他边界条件则保持不变。考虑到Lucky Strike 热液区位于慢速扩张洋中脊的构造背景下，更加充分的洋中脊构造伸展作用使其洋壳渗透率较快速扩张环境明显提升[39]，因此，我们赋予模型相对EPR 9°17′N 热液模型更高的均一渗透率（约5×10−15m2）。将模型运行至100 ka 以确保其到达稳态。

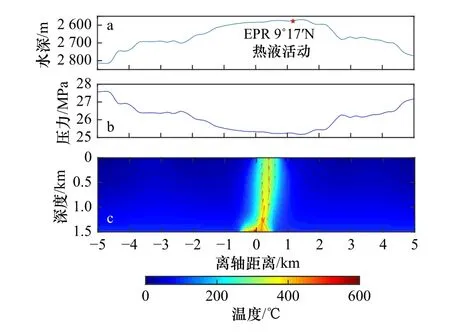
图5 基于EPR 9°17′N 热液区地形剖面的数值模拟结果Fig. 5 Simulation result based on the bathymetric profile of the EPR 9°17′N venta. EPR 9°17′N 热液区跨轴剖面; b. 基于水深剖面计算的海水压力剖面; c. 稳态数值模拟结果，离轴距离为0 代表洋脊轴的位置a. Cross-axis profile of EPR 9°17′N vent; b. calculated seawater pressure profile; c. running result in steady-state, distance=0means the location of ridge axis

图6 基于Lucky Strike 热液区地形剖面的数值模拟结果Fig. 6 Simulation result based on the bathymetric profile of the Lucky Strike venta. Lucky Strike 热液区跨轴剖面; b. 基于水深剖面计算的海水压力剖面; c. 稳态数值模拟结果，离轴距离为0 代表洋脊轴的位置a. Cross-axis profile of Lucky Strike vent; b. calculated seawater pressure profile; c. running result in steady-state, distance = 0means the location of ridge axis

在稳态的数值模拟结果中，洋壳内部稳定发育一个规模相对较小（宽度约为500m）的高温（约300℃）热液羽，并发生约800m 的离轴偏移（图6c），最终导致热液海底喷发位置与Lucky Strike 热液区的实际位置保持很好的吻合效果。因此，该模型可以较好地模拟出实际的Lucky Strike 热液对流系统的形态和喷发位置。

5.3 对流模型的建立

基于上述地形起伏相关的热液系统偏移程度的解析模型（图4）和符合实际热液系统的模拟结果（图5，图6），关于洋底地形起伏聚集上涌热液流体的理论模型最终得以建立（图7）。在该模型中，洋壳内部辉绿岩墙底界的透镜状岩浆熔融体作为上部新生洋壳的来源[3]和维持区内热液循环系统的热源，低地形部分及其下伏渗透性洋壳表现为主要的海水充注区域，而高地形由于上覆海水压力的相对减小，使其成为热液上升、释放和喷发的主要汇集区域（图7）。