细分双冠图的拉普拉斯矩阵的广义逆及其应用
2020-10-10刘家保陈靓
刘家保,陈靓
(安徽建筑大学 数理学院,安徽 合肥230601)
0 引言
在本文中,所考虑的图都是简单无向图。图G的顶点集为V( )G ={ }v1,v2,…,vn,边 集 为E( )G ={ }e1,e2,…,em,被表示为G =(V(G),E(G))。图G 的邻接矩阵A(G)是一个阶数为n 的方阵,如果顶点vi和vj邻接,它的( )i,j 的元素等于1,否则等于0。设dG( )vi是顶点vi的度,它的度矩阵D( )G 是一个对角矩阵,对角线元素为dG( )vi。图G 的拉普拉斯G - A( )G = D( )G 。设M( )G 表示矩阵被定义为L( )G 的点边关联矩阵,是一个n×m 的矩阵,如果vi邻接于ej,它的元素是1,否则,它的元素为0。
矩阵理论不仅是经典数学的基础,同时也是有实用价值的数学理论,被广泛应用于不同的学科领域,在理论和实践中都起着十分关键的作用。矩阵广义逆目前应用于系统辨识、控制论、规划论、测量、计量学和统计学等多方面。
Klein 和Randić 于1993 年定义了图的电阻距离的相关概念,它是一种新的图的度量[1]。如果每个边用一个单位电阻来代替,那么在两个顶点之间的有效电阻距离用Rij表示。Klein 于2002 年给出了电阻距离总和的一些规则[2],关于电阻距离的其他结果可以看[3-5]。在各种不同的图中,计算任意两点间的电阻距离是最近的热点问题之一。图的拉普拉斯矩阵广义逆可以用来计算连通图中任意两点之间的电阻距离。2014 年,卜长江教授用广义逆理论的方法给出了“大图”的电阻距离可由“小图”的电阻距离计算而得到[6],更多图的电阻距离可以看[7-11]。受以上工作的启发,本文将研究细分双冠图的拉普拉斯矩阵广义逆和细分双冠图中任意两点之间的电阻距离。
本文的接下来部分组织如下。在第1 节中,主要介绍一些定义和引理。在第2 节中,给出主要结果和证明。在第3、4 节中分别给出了主要结果的应用例子和总结全文。
1 预备知识
在本节中,回顾一些矩阵理论的概念,介绍下文用到的定义和引理。
定 义1[12]设A ∈Cn×n,若X ∈Cn×n,满 足:AXA = A 则称为X 矩阵A 的{1 } -逆,记作A{1}.
定义2[12]设A ∈Cn×n,若X ∈Cn×n,满足下列条件:AXA = A,XAX = X,AX = XA 则称X 为矩阵A的群逆,记作A#.
定义3[12]矩阵A =( aij)m×n,B =( bij)p×q的克罗内克积A ⊗B 是一个mp×nq 矩阵,其元素可以通过用aijB 取代矩阵A 中aij得到。



M-1=( )A-1+ A-1BS-1CA-1- A-1BS-1-S-1CA-1- S-1,
其中S = D - CA-1B.

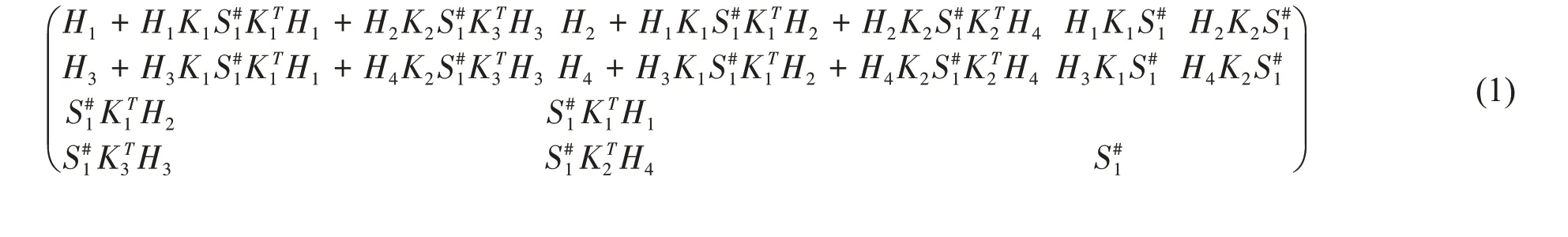
2 主要结果和证明
本部分,将给出细分双冠图的拉普拉斯矩阵的广义逆。
定理1:设G 是一个有n 个顶点,m 条边r -正则图,G1和G2分别有n1和n2个顶点,则式(1)是

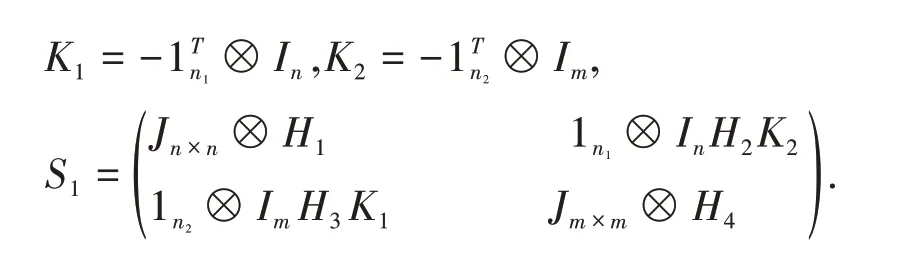
证明设1n表示维数为n,元素全为1 的列向量,Jm×m表示元素全为1 的m×n 矩阵,In表示元素全为1 的n×n 矩阵。类似的,0n表示维数为n,元素全为0 的列向量,0m×m表示元素全为0 的m×n矩阵。设M( G )表示G 的点边关联矩阵。设l( G)是G 的线图。根据图的拉普拉斯矩阵定义,图的L( G( S)∘{G1,G2} )的拉普拉斯矩阵可以表示为式(2)。

接下来计算S 和S-1,根据矩阵逆理论,由(3)式

得出(4)式,根据引理2,可以求出(5)式、(6)式和(7)式。
最后,令
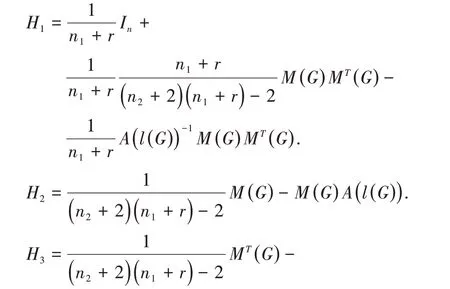
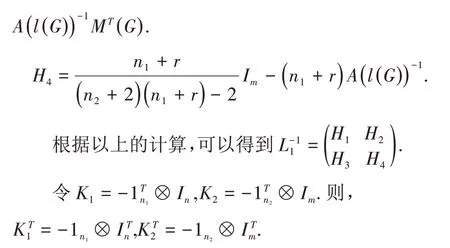
接着计算S1,根据引理1 和引理3,可以求得(8)式、(9)式、(10)式和(11)式。
最后根据引理2 和引理3,可以求得L( G(S)∘{G1,G2} )对称{1 } -逆为式(12),



从而,定理1 成立。
3 应用和例子
设Pn表示一个带有n 个顶点的路,图1 是P2(S)∘{P3,P2} 的图。



图1 细分双冠图∘{P 3,P2}

物理学中的欧姆定律,有r1,10= r1,3+ r3,10=. 这个结果和作者得到的结果是一致的,说明了本文的结果是有理论意义和实际价值的。
4 结束语
图的广义逆和电阻距离涉及图论、系统工程、网络化学、生物、线性规划等相关知识,其理论被广泛应用到电网路理论研究、复杂网络分析、化学分子的属性预测等领域。本文研究了细分双冠图的拉普拉斯矩阵的广义逆,求出了任意两点之间的电阻距离。对于其它图操作的广义逆,是进一步值得研究的主要方向。
