运营期地铁车站与下穿道路一体化结构的动力响应
2020-10-10翟朝娇程桦柳军修
翟朝娇,程桦,柳军修
(1.安徽建筑大学 建筑结构与地下工程安徽省重点实验室,安徽 合肥 230601;2.安徽大学 资源与环境工程学院,安徽 合肥 230601;3.安徽建筑大学 安徽省城市建设和地下空间工程技术研究中心,安徽 合肥 230601)
0 引言
随着城市人口的增加,人类生活节奏的加快,地面空间越来越紧张,城市交通问题日益凸显,地铁在缓解城市交通压力、拓展城市空间等方面发挥着重要的作用,以地铁为核心的城市轨道交通系统逐渐成为城市交通系统的重要组成部分。地铁在给人类带来快捷、便利、有序的交通和良好的乘车环境的同时,也存在着诸多问题,地铁运行所引发的结构振动问题,自地铁开始运营以来就一直受到人们的关注。
刘建达等[1]运用ABAQUS 建立了隧道-地基动力相互作用分析模型,分析了地铁列车运行引起的地表振动特性,给出了地铁隧道断面几何形式、隧道埋深、两平行区间隧道间的净距和场地条件等因素对地表振动特性的影响规律;Yang 等[2]运用有限元方法探讨了地铁运行引起的波的传播规律,分析了阻尼比、土层深度、隧道埋深,衬砌厚度、列车速度和频率等对地面振动的影响;唐益群等[3]以上海地区隧道为研究对象,用数值模拟和现场监测相结合的方法,得到饱和软黏土地区地铁振动荷载作用下隧道周围土体的变形,并进一步计算得到地铁振动荷载作用下引起的地面沉降量;宋文杰[4]利用FLAC3D 建立北京地铁10 号线双井站模型,分析了列车动荷载作用下地铁车站结构的力学性能;Patrícia 等[5]运用多结构数值计算方法研究了土体刚度对地铁运行引发的振动传播的影响;夏倩等[6]以地铁旁砌体结构为研究对象,对上海某线地铁振动进行了详细的数值分析,研究不同影响因素对振动响应分布规律影响;赵斌等[7]建立了车站结构-土的准三维有限元模型,分析车站结构型式对地铁诱发环境振动的影响;祁晓雨等[8]采用MIDAS GTS软件构建地铁车站数值计算模型,计算地铁列车运行振动对地铁车站及上部建筑造成的沉降,得出地铁列车运行振动对地铁车站及上部建筑沉降的影响;雷晓燕等[9]以大型综合交通枢纽车站南昌西站进行现场实测,研究地铁2号线列车运行荷载的振动传播规律及频率分布特点,分析综合交通枢纽车站站房结构的局部振动规律及频谱响应规律;张厚贵等[10]结合工程实际,从理论上分析了在列车运行引起的随机振动作用下,地下隧道钢筋混凝土结构产生疲劳破坏的机理,得到在地铁正常运营情况下,北京地铁2 号线隧道结构安全及正常使用的振动控制标准。以上学者对地铁动荷载下结构的动力响应问题的研究大多依托于某个特定的工程背景,不同的工程差别很大,其在动荷载作用下的动态响应也千差万别。
本文以合肥市地铁1 号线长淮站为依托,针对车站主体与下穿路面一体化结构体系,运用有限元软件Midas GTS NX 建立三维数值模型,分别计算地铁从车站左侧、右侧、双侧经过三种情况下路面沉降、车站一体化结构的动力响应,并将就计算结果与地铁隧道结构的安全标准值相对比,得到在正常运营情况下,长淮站车站一体化结构的动力响应处于安全允许范围内,研究结果对地铁的后期运营和维护具有重要的意义。
1 工程背景
长淮站位于胜利路与凤阳路交叉口处,沿胜利路南北方向布置。胜利路原状主路为双向六车道,辅路为一条机动车道,为保证胜利路方向交通畅通,在胜利路与凤阳路交叉口处设置下穿道路。长淮站车站主体与胜利路下穿道路一体化结构设置,即下穿路面结构直接施作在车站顶板上,车站围护结构作为下穿路的永久挡土结构。胜利路与凤阳路交叉口处下穿路上部设置梁、板结构形成下穿桥,保证凤阳路方向的交通。位于道路交叉口处沿凤阳路方向已建成畅通北一环高架桥上跨胜利路,桥桩距离一体化结构最近处约14 m,桥梁底部距离路面约为4.5 m。车站总宽23 m,与上部下穿路同宽。一体化结构为双层三跨框架结构,13.5 m岛式站台,采用明挖法施工车站与下穿道路平面布置情况如图1 所示。
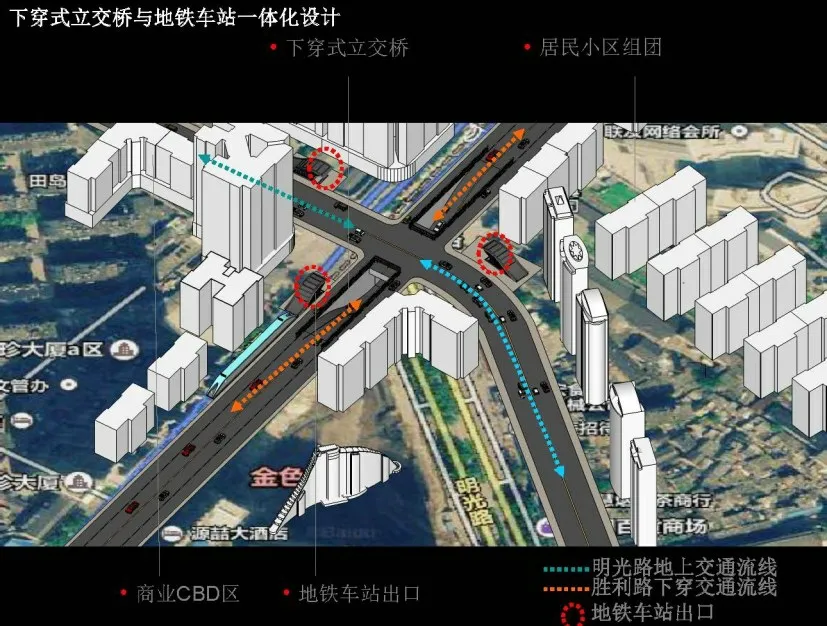
图1 车站与下穿道路平面图
勘探揭露的场地主要土层和物理力学指标如表1 所示。

表1 土层物理力学参数
2 数值计算
2.1 参数选择
地铁站结构剖面宽23 m,埋深为16.5 m,纵向长184.5 m。地连墙底板以下嵌入深度取13 m,抗拔桩长度为15 m、17 m 间隔布置。距车站始端36.3 m~119.6 m 处设有下穿桥,桥梁板距路面6.75 m。车站主体结构混凝土强度等级:车站顶板、顶纵梁C35;侧墙、底板、底纵梁及端墙C35。中板、中纵梁及加强梁C35;中柱C50;底板回填素混凝土C30。所有结构均设置为各向同性模型。
2.2 模型建立
本文采用Midas GTS 数值分析软件进行地铁车站运营期的数值模拟,具体模型参数如下:影响深度取开挖深度的3-4 倍,影响宽度取车站宽度的2 倍,最后整个模型宽116.1 m、高70 m,纵向长度为275.4 m。整体模型采用先划分平面网格,再进行纵向拓展的方法,考虑到计算模型的网格划分对计算结果的影响较大,故对一体化结构的网格密度做了适当的加密以满足计算精度的要求,模型共包括58 889 个单元和51 744 个节点,本构模型采用摩尔库伦模型,结构单元是Midas GTS 自行连接,结构和土体因刚度相差较大,采用界面单元连接,法向和切向约束均是非线性变形。建立如图3、图4 的三维数值计算模型。

表2 材料相关参数
车站主体结构主要承受人行、车辆、列车三种荷载,人群荷载作用在中板和沿凤阳路梁板上,考虑最不利因素,中板和梁板上布满人,则人群荷载密度0.7 kN/m2,研究表明车辆动荷载冲击系数随车速、路面波长(不平整度)变化,但其量值始终处于0.1~0.4 之间,考虑最不利因素,下穿路面布满车辆,冲击系数取0.4,车辆面荷载为21 kN/m2。合肥市地铁1 号线采用六辆车编组,荷载可根据图2(所示为两节车厢)计算,并考虑冲击力的影响。选用列车通过时实测的道床振动速度时程,车站长185.4 m,列车全长112.4,二者相差不大,为方便计算,近似假设列车荷载为作用在道床表面的沿轨道方向无限长同相位振动,将列车荷载以速度方式直接施加到地铁车站上,冲击系数取0.3,参考合肥地铁运营速度,列车平均时速取60 km/h。

图2 车辆编组简图
3 计算结果与分析
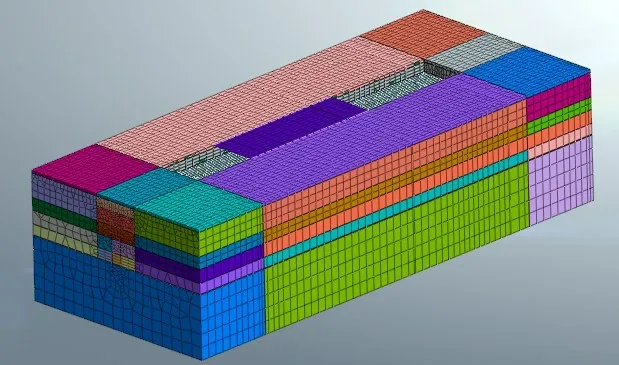
图3 三维模型图

图4 剖面图
地铁运行时产生的动荷载的形式具有多样性,即可以是单一列车动荷载作用的情况,也可以是多个动荷载同时作用的情况。基于这一点的考虑,本文分三种情况建立模型,分别为仅在车站左侧有地铁经过的情况,左右两侧都有地铁经过的情况以及仅在车站右侧有地铁经过的情况,左右两侧列车行驶方向相反。
3.1 静荷载作用下梁板的响应
不考虑列车荷载,将人群荷载和车辆荷载以静力的形式施加在下穿道路之上,得到车站模型的竖向位移和竖向应力,如图5、图6。
由图5 可知,人群、车辆静荷载作用下车站梁板结构的竖向最大位移为8.136 mm,位于顶板中部,梁板结构整体位移呈中间大,两端小的趋势。由图6 可知,梁板的最大竖向应力为10.8 MPa,位于纵向距车站中板中部。位移与应力符合梁板静力作用下的基本特性,证明了本数值模型的准确性。
3.2 列车动荷载作用下路面沉降
列车从车站左侧通过、右侧通过、双侧通过时,下穿路面的累积沉降图为图7、图8、图9。由图7-图9 可知,当列车动荷载分别作用在车站左侧和右侧时,其引起的下穿路面最大沉降均位于荷载作用侧路面的前后两端,其值分别0.315 mm、0.318 mm,两种情况相差不大。而由图9 可知,列车动荷载同时作用于车站两侧时,下穿路面最大沉降位于路面的正中心,其值为0.389 mm,成中间大两头小,说明双侧通车对路面沉降的影响比单侧通车稍大。
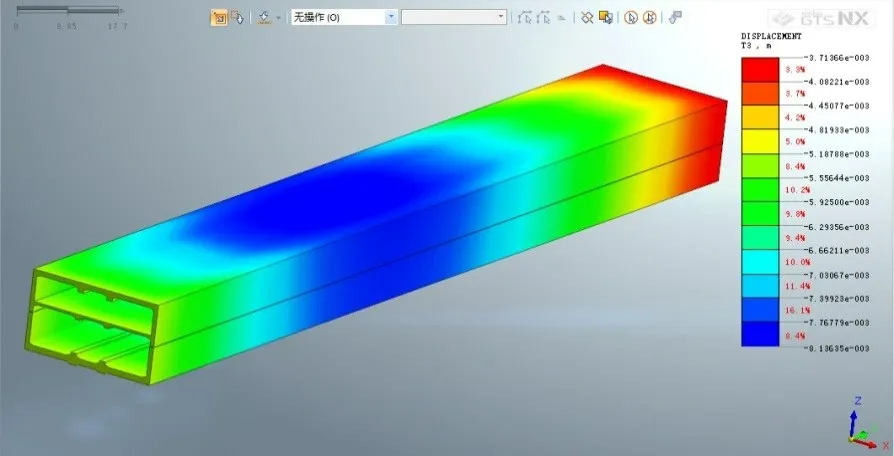
图5 人群、车辆静荷载下的梁板竖向位移

图6 人群、车辆静荷载下的梁板竖向应力

图7 列车荷载作用在车站左侧时下穿路面沉降包络云图

图8 列车荷载作用在车站右侧时下穿路面沉降包络云图
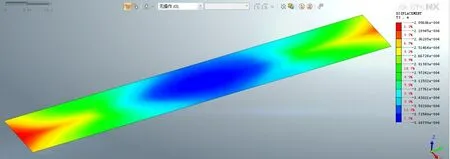
图9 列车荷载作用在车站两侧时下穿路面沉降包络云图
列车从车站双侧同时通过时整体模型位移如图10 所示,由图10 可知,列车从车站双侧同时通过时引起的地(路)面沉降沿车站纵向中心线基本呈左右对称,且中间大两端小,距离列车荷载越远沉降越小,车站两端大约23 m 以外的土体基本不会产出地面沉降,说明列车荷载对地面沉降的影响是有范围的,超出这一区域,列车荷载对地面沉降的影响可以忽略不计。
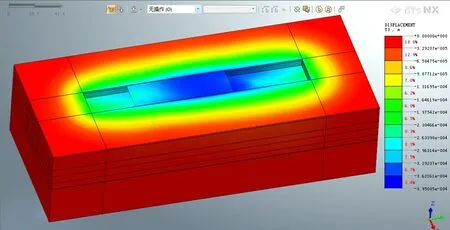
图10 列车荷载作用在车站两侧时整体模型沉降包络云图
3.3 列车动荷载作用下车站主体结构动力响应
车站长185.4 m,列车全长112.4。若将车头到站时刻设为0 秒,则车尾出站的时刻为17.87 秒。本文将动力响应的研究时间定为0~30 秒。由于地铁运行时所引起的振动主要表现为竖直方向上的振动,故本文只分析结构沿竖直方向的动力响应。
列车从车站左侧通过、右侧通过、双侧通过时,一体化结构速度响应包络云图为图11、图12、图13。由图11-图13 可知,左侧通车和右侧通车时,一体化结构的速度基本相同,竖直方向最大速度分别为0.3149 mm/s、0.3505 mm/s,双侧通车时竖直方向最大速度为0.3566 mm/s,略大于单侧通车时的速度响应。说明双侧通车时的动力响应并不是简单地把两个单侧通车工况下的动力响应数值相叠加,这是因为双侧通车时的荷载虽然增加了,但是两侧荷载中心对称的加载方式会减小一体化结构的振动响应。
为更好地说明以上计算结果,将列车从车站左侧通过、右侧通过、双侧通过时梁板的动力响应结果汇总,结果如表3。

图11 左侧通车时车站梁板速度包络云图
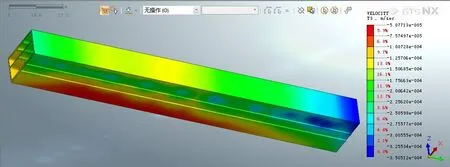
图12 右侧通车时车站梁板速度包络云图
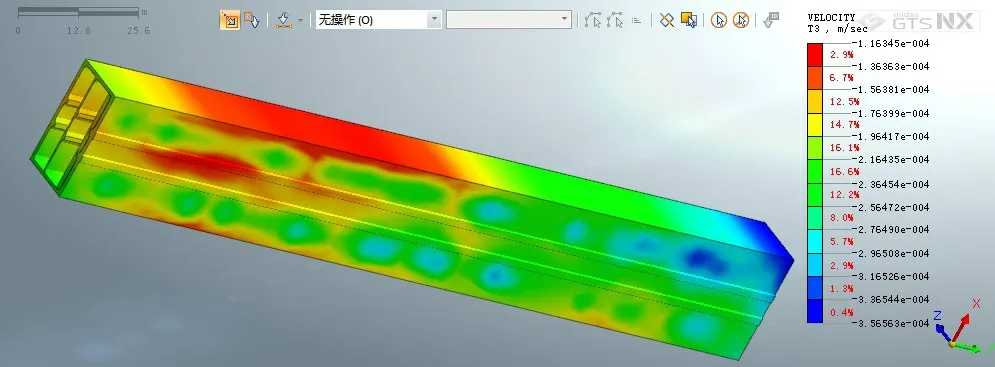
图13 两侧通车时车站梁板速度包络云图
三种情况下,车站与下穿一体化结构速度响应最强的位置均为:纵向距车站末端30 m 左右,底板的动力响应最大,其后依次是中板、顶板、中间柱、侧墙。造成速度响应纵向不对称的情况主要是因为下穿桥位于车站的前段,并不是纵向对称的,桥梁增加了前段结构的刚度,使后段的速度响应强于前段。

表3 梁板响应汇总表
地铁隧道结构的安全振速标准值为2.5 mm/s[10],同时从上图11、图12 以及图13 可以看出,当车站有地铁运行时,一体化结构在竖直方向产生的最大速度没有超过一体化结构振动影响控制标准值2.5 mm/s,一体化结构处于安全允许范围内。
3.4 列车动荷载作用下车站梁板加速度时程曲线
列车双侧通车比单侧通车时车站的动力响应更强,因此选取列车双侧通车时车站顶板、中板、顶板、中间柱和侧墙加速度最大的点,绘制加速度时程曲线,如图14。从图中可以看出,最大加速度为14.020 mm/s2,出现在车站底板位置,车站中板的最大加速度时程曲线与顶板的相似且略小于底板,车站顶板、中间柱和侧墙的加速度响应要小得多,前者约为底板的0.5,中间柱和侧墙的加速度响应约为底板的0.2~0.25,因此从车站后期安全运营的角度来讲,应该适当加强底板和中板的抗振性能。
4 结论与讨论
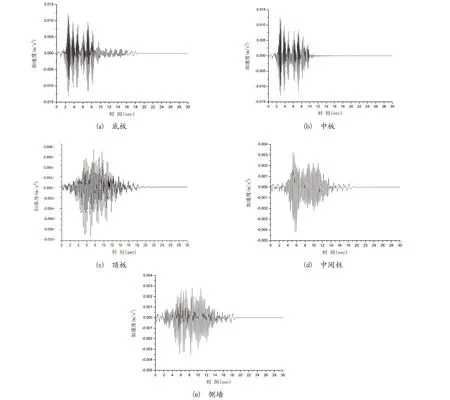
图14 两侧通车时一体化结构竖直方向加速度时程曲线
本文通过对合肥地铁一号线长淮站车站与下穿一体化结构在地铁运营期的动态响应进行计算,可以得出以下结论:
(1)当列车动荷载分别作用在车站左侧和右侧时,其引起的下穿路面最大沉降均位于荷载作用路面的前后两端且相差不大,当列车动荷载同时作用于车站两侧时,下穿路面最大沉降位于路面的正中心,成中间大两头小,说明双侧通车对路面沉降的影响比单侧通车稍大。
(2)左侧通车、右侧通车和双侧通车时一体化结构的动力响应差别不大,三种情况下,一体化结构动力响应最大点位于纵向距车站末端30 米左右,底板的动力响应最大,其后依次是中板、顶板、中间柱、侧墙。
(3)计算结果表明车站运营期一体化结构在竖直方向产生的最大速度没有超过振动影响控制标准值,处于安全允许范围内。
(4)本文的研究基于有限元法进行,不能实现与监测数据做对比,后期的研究中计划开展现场实测以完善这方面的工作。
