改进的SLIC超像素图像分割与合并算法

刘安琪，刘华勇，王焕宝，

(1.安徽建筑大学 电子与信息工程学院，安徽 合肥 230601；2.安徽建筑大学 数理学院，安徽 合肥 230601)

0 引言

随着科学技术的发展，可视化设备的画面变得越来越清晰，设备所生成图像的尺寸剧增。早期的图像分割技术效率较低，且不能在高分辨率的图像中保持较好的实时性。为了解决高像素图像的分割问题，Ren[1]提出了超像素的概念。迄今为止，超像素分割算法基本分成两种。一种是基于数学中图论的方法；另一种则是基于聚类思想的梯度上升方法[2]。基于图论的超像素分割方法包括Ncuts[3]、Graph Cuts[4]、Grab Cuts[5]等；基于梯度上升的超像素分割方法包括Mean Shift[6]、Turbopixel[7]、SLIC(Simple Linear Iterative Clustering，SLIC)[8]等。其中SLIC 超像素分割算法(后文简称为SLIC 算法)在时间复杂度、边界召回率以及分割错误率等方面优于前两者。近年来，国内外研究人员提出了多种基于SLIC 算法的改进形式[9-11]。文献[9]提出的有偏聚类提升了算法的计算效率，但在欠分割问题的处理上效果不够明显；文献[10]近邻分类虽提升了算法的计算效率，但欠分割问题未得到解决，分割结果的边缘贴合度也有待提高；文献[11]提出的区域合并仅建立在颜色特征上，并未融入图像的纹理特征。本文提出的采用像素抽样、基于纹理特征的K-means 聚类对SLIC 算法进行改进，提升算法的计算效率的同时对欠分割区域进行修正。最后在改进的算法分割结果基础上结合双向邻域图分割结果进行区域合并。

1 相关算法

1.1 SLIC算法

SLIC 算法首先将图像从原来的RGB 颜色空间转变为CIELab 颜色空间；然后结合CIELab 颜色空间的三个分量和像素点在图像中的位置信息构建一个5 维的特征向量Pi=[li,ai,bi,xi,yi]，i 是像素的下标；最后对图像中的像素点进行局部聚类处理。算法步骤如下：

步骤1：种子点的初始化

假设输入图像共有N 个像素点，分割结果预计需要得到K 个超像素块，那么每个超像素块中应有约N K 个像素点，种子点间的距离约为S =N K。选取种子点时，为了降低其落在图像边界的位置的可能性，会在原种子点的3×3 区域内寻求一个梯度最小的位置作为新种子点。每个种子点代表一个类别。

步骤2：衡量相似度

在给定的步长范围内，计算每个像素点与种子点间的相似度。SLIC 的相似度度量方法如下。

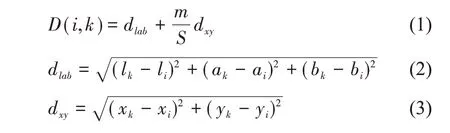
dlab为像素间的颜色距离。dxy为像素间的欧式距离。D(i,k)的值代表像素点i 与种子点k 间的相似度，D(i,k)越小则越相似。m 为权重参数，取值范围为[1，40]。

步骤3：像素点分类

根据相似性度量结果，像素点类别与其相似度最高的种子点的类别保持一致。重复步骤2、步骤3，直到聚类结果无显著变化或达到要求的迭代次数。

步骤4：后续处理

结合连通性准则，将多连通及面积过小的超像素块与其相邻的大超像素块合并。

1.2 K-means算法

K-means 聚类算法通过像素与种子点间的欧氏距离来衡量像素间的相似度，将像素点分成多个类别[12]。K-means 聚类算法原理简单、对低维且相对集中的数据具有较好的分类效果。K-means 算法具体步骤如下。

输入：待聚类图像。

输出：聚类结果。

步骤1：初始化K 个种子点(K≥2)；

步骤2：比较所有像素点到种子点间的欧氏距离，像素点类别与欧氏距离最小的种子点保持一致；

步骤3：计算类中所有像素的平均值，将均值作为新的种子点；

步骤4：重复上述步骤2、步骤3，直到聚类结果不再发生明显变化或达到要求的迭代次数为止。

2 本文算法

2.1 像素抽样

相比于SLIC 算法，本文算法首先对待分割图像进行像素点的间隔抽样，抽样方式如图1 所示。

图1 像素采样

其中，黑色部分为采样像素点，白色部分为未采样像素点。对于采样部分的像素点，采用公式(1)计算；对未采样部分像素点，以如图2 所示的每9 个像素为单位，用像素点间的相关性进行标签分配。由像素间的相关性可知，一个像素的标签大概率与其相邻的像素保持一致。根据这一性质，在计算1 号像素的标签时，只计算1 号像素和其左右相邻的两个已知标签像素间的颜色距离dlab。其余像素点均可用上述方法求出标签，5 号像素需要与其相邻的四个像素点计算相似度。

图2 未采样像素标签分配

2.2 基于纹理特征的K-means聚类修正

2.2.1 灰度共生矩阵

灰度共生矩阵是一种基于统计方法的描述图像纹理特征的方法。灰度共生矩阵定义为从灰度级i 的点离开某固定的位置关系d =(Dx,Dy)以达到灰度为j 的概率Pd(i,j)=(i,j = 0,1,2,3,...,L -1)。其中，i，j 分别表示像素的灰度值，L 为图像的灰度级，d 表示两个像素间的步长；i 与j 间的夹角θ 表示灰度共生矩阵生成时的方向[13]。示意图如图3 所示。

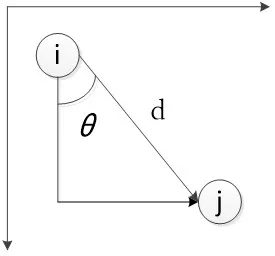
图3 像素与角度的关系

步长确定后，图像的灰度共生矩阵的一般形式如式4 所示。

d 分别取1、2、3 时的纹理图像如图4 所示。

图4 不同步长d的纹理分割结果

由图4 可知，当步长d 较小时，纹理更为细致。本文利用纹理特征修正超像素分割结果中的欠分割区域，即图像中的子块，要对纹理特征进行精细的表征，所以本文中步长d 取为1。

2.2.2 灰度共生矩阵的特征表示

灰度共生矩阵共有14 种纹理特征值，其中应用较广泛的有4 种，分别为能量、对比度、相关度以及熵。本文选取对比度和熵表征图像的纹理特征。

对比度是度量灰度共生矩阵的值是如何分布和图像中局部变化的多少，反应了图像的清晰度和纹理的沟纹深浅。对比值越大，反差越大，效果越清晰；反之，对比值小，则沟纹浅，效果模糊。对比度的计算如式(5)所示。

熵可以衡量信息量，纹理是一种信息，由此熵也可以衡量纹理。熵反映了图像中纹理非均匀度或复杂性。纹理越复杂，熵值越大。熵的计算如式(6)所示。

计算特征值前，先确定计算过程中的相关参数。本文选择3×3 大小的滑动窗口进行特征值计算，步长d 设为1，方向选取0 °、45 °、90 °、135 °等4 个方向。

综上所述，基于纹理特征的K-means 聚类修正算法步骤如下。

输入：初始分割结果。

输出：修正结果。

步骤1：灰度级量化

计算灰度共生矩阵时，为避免大计算量，将灰度级量化为8 个灰度级。

步骤2：计算纹理特征值

通过灰度共生矩阵计算4 个方向上的对比度和熵，然后计算两个参数在4 个方向的均值，作为窗口中心像素的最终纹理特征。

步骤3：

移动窗口，重复步骤2，直到遍历完所有像素点为止。

步骤4：

用所求的对比度和熵来代替传统K-means 聚类中像素的位置信息，对欠分割区域进行聚类，直至达到所设聚类次数为止。

2.3 双向邻域图区域合并

对修正后的结果，用区域邻接图(Region Adjacency Graph，RAG)将分割结果映射为一个无向图G=(V，E)[14]。其中V 为图中结点的集合，代表分割结果中的超像素块，E 为图中边的集合，代表超像素块间的相邻关系。构造区域邻接图的过程如图5 所示。

RAG 能记录所有区域间的关系。但若得到的初始分割区域数量太多，会造成RAG 的节点数量和边的数量过多，从而造成计算复杂度增大，这时可采用双向邻域图(Bidirectional Neighbor Graph，BNG)对RAG 进行改进。一个已确定的RAG，其改进形式BNG 为Gm=(Vm,Em)。Gm表示有向图，Vm表示原RAG 中所有节点的集合，Em是有向边的集合。BNG 中的每个节点都有一条有向边指向与该节点最相似的节点。RAG 转换为BNG 过程如图6 所示。

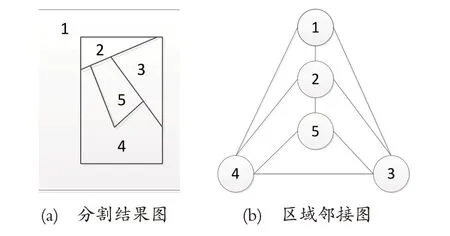
图5 构建区域邻接图

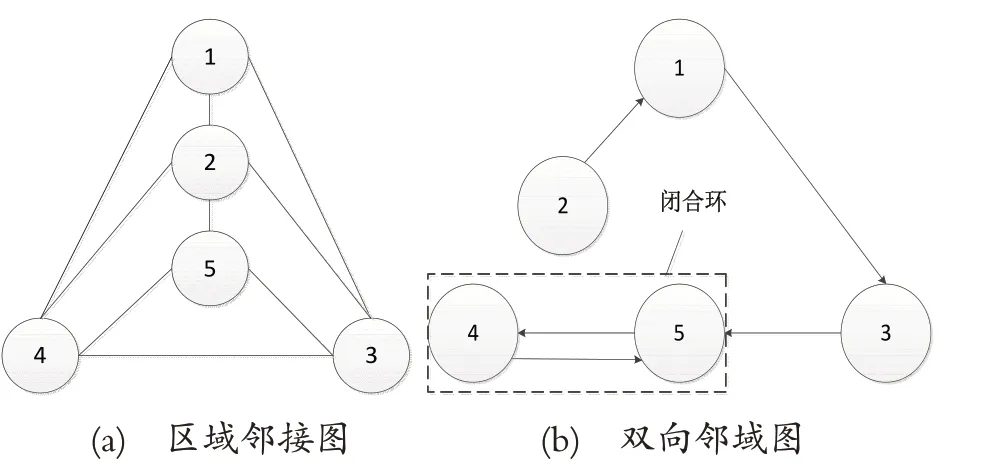
图6 构建双向邻域图

由RAG 转换为BNG 时，在RAG 中需保留全部边，而在BNG 中只需保留部分边，合并时每次只合并闭合环两端的区域，大大提高了计算速度，加快了合并效率。改进的区域合并算法步骤如下：

输入：初步分割结果图。

输出：最终分割结果。

步骤1：对输入的分割结果图进行RAG 的构建；

步骤2：计算每个区域与其相邻区域的相似度，将RAG 转换为BNG；

步骤3：在BNG 中先对闭合环两端的节点进行合并，所有闭合环合并完成后，更新BNG；直到循环结束为止；

步骤4：输出合并结果。

2.4 相似性度量

2.4.1 颜色特征

颜色特征是图像最基本的特征之一。本文采用超像素块的颜色直方图对颜色特征进行描述。为简化计算，对RGB 颜色空间中的3 个分量作均匀量化处理，由原来的256 级降为16 级，则共有4096 级颜色；再用巴氏系数计算超像素块间的相似性，计算式如式(7)所示。

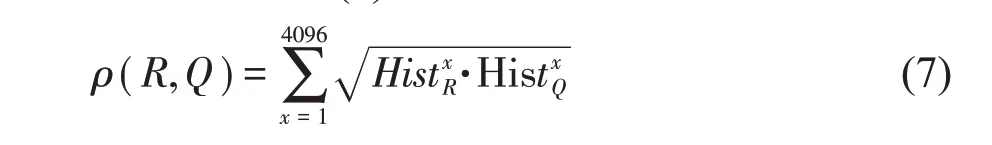
2.4.2 纹理特征

局部二进制模式(Local Binary Patterns，LBP)是由Ojala[15]等提出的一种纹理描述算子。其定义为在3×3 的窗口内，以窗口中心像素的灰度值为阈值，与相邻的8 个像素的灰度值比较，若周围的像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样3×3 邻域内的8 个点经比较可产生8 位二进制数，即得到该窗口中心像素点的LBP 值。LBP 计算式如(8)所示。

式中(xc,yc)为中心像素，ic为中心像素灰度值，ip为相邻像素灰度值，s(·)为符号函数，定义如式(9)所示。

本文采用LBP 提取纹理特征。首先，将超像素块分成4×4 的16 个区域；然后，计算每个区域的归一化灰度直方图；最后，整合16 个区域的归一化灰度直方图，利巴氏系数来计算超像素块间的相似性，计算如式(10)所示。

A 为区域数量，HistvQ和HistvR分别表示区域Q和R 的归一化灰度直方图，v 为元素下标，α(Q,R)的值越大，区域Q 和R 间的相似度越大。

综上所述，本文区域间的相似性度量计算如式(11)所示。

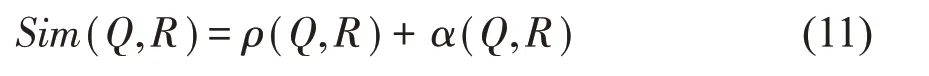
本文算法步骤如下：

输入：待分割图像。

输出：分割结果。

步骤1：像素抽样处理；

步骤2：对抽样像素点与未抽样像素点进行标签分配，得到初步分割结果；

步骤3：采用基于纹理特征的K-means 聚类方法修正欠分割区域；

步骤4：提取超像素块的颜色与纹理特征，利用双向邻域图进行合并，得到最终分割结果。

综上所述，本文算法流程如图7 所示。

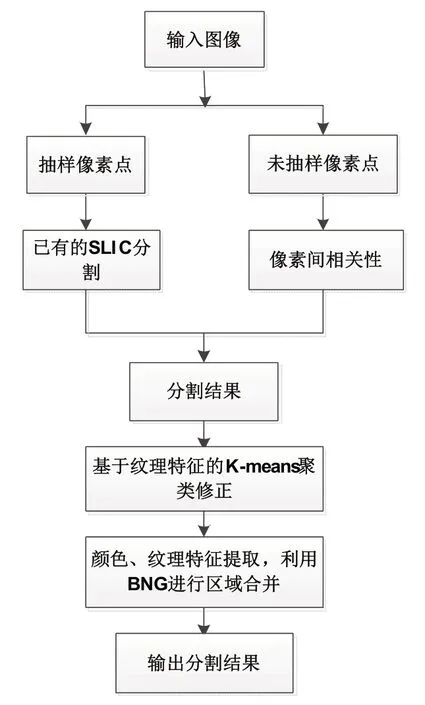
图7 算法流程图

3 实验结果与分析

3.1 实验结果

本文实验所用图片均来自BSD500 数据集。图8 为SLIC 算法分割结果图，其中a 为原图，b、c、d 分别对应为超像素块K 取100、500、1000 的分割结果。

SLIC 算法的分割结果有时会存在背景与目标区域没有完全分开的欠分割情况，如图9 所示。用本文提出的改进的SLIC 超像素分割算法对图像进行分割，分割结果如图10 所示。从图中可以看出，欠分割区域经过基于纹理特征的K-means 聚类修正后，树干基本与天空完全分离。

对修正后的分割结果构建双向邻域图，利用结合颜色与纹理特征的相似性度量公式计算区域间的相似度，进行区域合并，结果如图11 所示。

图8 不同K值的分割结果图

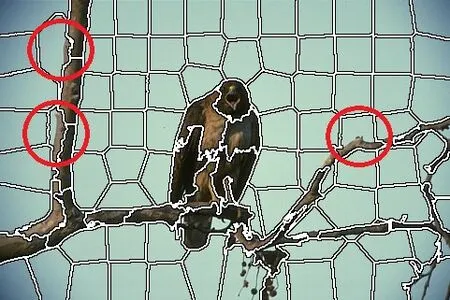
图9 分割结果中的欠分割区域

图10 欠分割区域的修正

图11 BNG区域合并结果

3.2 实验对比

3.2.1 不同权重m 与欠分割的关系

m 为调节颜色距离的权重，起着调节像素点间颜色距离与欧式距离比重的作用。由图12 可知：m 较小时，分割结果的欠分割错误率低；而当m 较大时，分割结果的欠分割错误率较高。但当m 较小时，虽取得了较低的欠分割错误率，但超像素块多以扁平、细长为主，形状不规则，紧凑度较低，不利于超像素的后续处理。当m 较大时，分割结果的欠分割错误率较高，但所得的超像素块形状规则，紧凑度较高。所以综合分析，当m 取15、20、25时，所得分割结果的超像素块相对规则，紧凑度相对较高，同时也能取得不错的欠分割错误率。

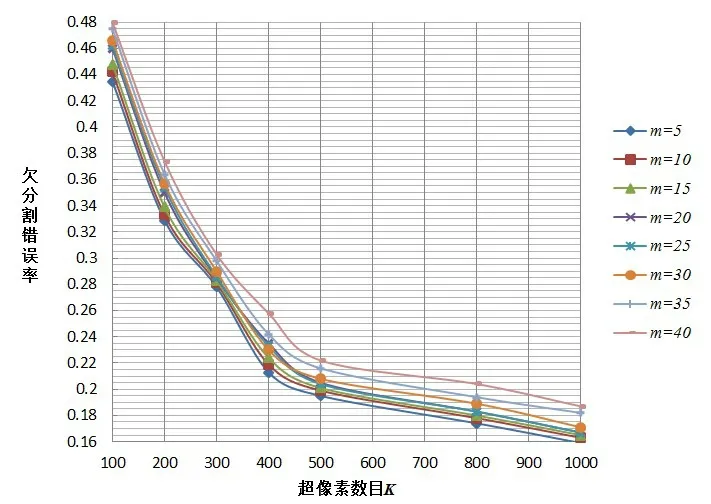
图12 权重m与欠分割错误率的关系

3.2.2 时间对比

表1 展示了四种超像素分割算法分割同一图像时所用时间。由表1 可知，SLIC 算法在计算速度上优于其余三种超像素分割算法。

表1 不同超像素分割算法时间对比

在SLIC 算法中，每个像素点在2S×2S 的范围内搜寻种子点，示意图如图13 所示。在规定搜索空间中每个像素点最少计算1 次，最多计算9 次。在本文算法中，采样部分的像素利用原相似度度量公式进行计算，采样部分的像素约占总像素的四分之一。对于未采样部分的像素点，以每9 个像素点为一个计算单位，利用像素点间的相关性，采用颜色距离公式进行相似度计算，计算式由五维降到了三维。在计算次数上，由原来的1 到9 次计算降到了现在的0 次、2 次或4 次。改进的SLIC 算法从计算公式维度和像素点的计算次数两个方面对SLIC 算法进行改进，提高算法的运算速度。表2为SLIC 算法与本文算法在K 取不同值时，每个像素点的计算次数统计。

图13 搜索示意图

表2 不同K值的像素点计算次数

图14 展示了不同K 值下未加入纹理修正和加入纹理修正的时间与SLIC 算法的时间对比。由表2 可知，在K 取不同值时，SLIC 算法像素点的计算次数约为本文所提方法的2 倍，这在图14 中得以体现，经过像素抽样后获得不同K 值的分割结果所需时间约为SLIC 算法的一半。在加入对欠分割区域的修正处理后，时间消耗虽有所增加，但仍低于SLIC 算法所用时间。

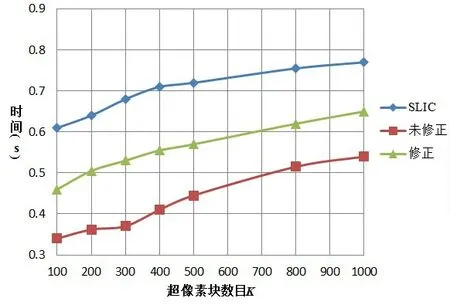
图14 时间对比

3.2.3 客观评价标准

边界召回率是衡量算法生成的边界之间和真值边界的一致性程度的指标。边界召回率越高，说明算法生成的边界越贴近真值边界。边界召回率定义如式(12)所示。

其中B(g)和B(s)分别为超像素边界真值和算法生成的超像素边界的集合。I(·)为指示函数，如果算法生成的超像素中的边界像素位于超像素真值中的边界像素范围之内，则返回1；否则返回0。Area(s)表示集合s 的面积。

欠分割错误率计算的是算法生成的超像素块和真值间不重合部分的比值。欠分割错误率的定义如式(13)所示。

其中gi为Ground Truth 中的第i 个部分。S是超像素算法对目标的分割结果，sk为S 中第k 个超像素块。运算符||表示超像素区域内像素点的数量。

表3 展示了不同超像素分割算法分割同一图像时的边界召回率与欠分割错误率的对比。

表3 不同超像素分割算法BR和UE对比

由表3 可知，相比于其余3 种超像素分割算法，SLIC 算法的边界召回率最高，欠分割错误率最低。

图15 为本文算法与SLIC 算法的客观评价对比。由图15 可知，本文算法在边界召回率上要优于SLIC 算法，说明本文方法相较于SLIC 算法能获得更好的边界贴合度。在欠分割错误率方面，当超像素数目小于500 时，本文方法的欠分割错误率要低于SLIC 算法；当超像素数目大于500 时，本文方法与SLIC 算法的欠分割错误率非常接近。综上所述，本文方法在超像素的客观评价结果中要优于SLIC 算法。

4 结论

图15 本文算法与SLIC算法的客观评价对比

本文在SLIC 算法的基础上，提出一种改进的SLIC 图像分割算法。针对SLIC 方法对分辨率高的图像进行分割时的时耗问题，利用像素抽样和像素间的相关性对图像进行分割。在运行速度上，本文算法相比于SLIC 算法，提升了约22%。同时，为了减少分割结果中的欠分割现象，采用基于纹理特征的K-means 聚类对欠分割区域进行修正。修正后的分割结果的边界召回率也优于SLIC 算法。最后，以颜色和纹理特征相结合征构建相似性函数，利用双向邻域图合并超像素块。实验表明，本文算法在时间复杂度与客观评价上均优于SLIC算法。