带微型扰流片旋转稳定弹气动特性分析
2020-10-09常思江
钱 龙,刘 丹,常思江
(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.西北工业集团有限公司 设计二所,陕西 西安 710043)
在众多弹道修正方案中,扰流片作为一种新型二维修正气动执行机构具有结构简单、执行动作简捷、成本较低等优势,有相当大的发展前景。作为一种新型弹箭变外形控制方式,扰流片组件采用微型电子机械装置,可以节省能耗,减小外形尺寸,还可以提高弹箭机动性,扩大作战范围。目前以尾翼弹为平台开展的扰流片应用研究较多:Dykes等[1]研究微型扰流片作用机理及其对弹丸飞行姿态的影响,该研究表明,这种控制方式能够有效提高弹箭的气动控制效率;Scheuermann等[2]采用计算流体力学和刚体动力学耦合模型,对超声速尾翼弹的微型扰流控制系统进行分析,并与靶道纹影实验结果进行对比,在阻力增加较小的情况下,该弹在3 km射程上具有80 m的侧向机动能力;Leonard等[3]针对尾翼弹扰流片排布优化问题进行研究,探索了尾翼的存在对扰流效果的影响,发现无尾翼时扰流片产生的控制力和力矩约为有尾翼时的一半;国外文献[4-7]也对此进行了研究,此处不再赘述。国内方面,刘凯等[8]研究了扰流片机构在尾翼弹上应用的可行性及修正特性。与之相对的是,以旋转稳定弹为平台的扰流片应用研究较少。Fresconi等[9]利用六自由度弹道模型进行了该概念的可行性验证,结果表明,弹道修正范围大于弹道散布,故弹丸具有足够的机动性,并可稳定飞行;法国国防部为专门研究旋转稳定弹的二维修正技术,设立了一个名为MANEGE的项目;文献[10-11]将扰流片控制执行机构应用于155 mm口径弹丸,对不同初速、射角下的修正能力进行了研究,结果表明,任何射击条件下在弹道末端激活扰流片即可使修正距离大于无控散布范围;文献[12]对扰流片外形结构的优化问题进行了研究,提出采用克里金模型和人工神经网络作为获取扰流片气动力系数的代理模型,文中指出,在给定扰流片展开时间的条件下即可确定其最优结构。国内对于微型扰流片机构在旋转稳定弹上的应用尚未见报道。以往文献偏重于对尾翼弹扰流机构开展研究,而微型扰流片在旋转稳定弹上的应用研究相对较少,亟待深入探讨。
微型扰流片应用于旋转稳定弹,首要涉及的是气动特性问题。本文以带微型扰流片的旋转稳定弹为研究对象,分析了不同来流马赫数下扰流片对弹丸轴向力、法向力和静力矩的影响,研究了扰流片高度、弧长变化对扰流片表面以及靠近扰流区域的弹体表面压力分布的影响,在一定条件下得到了扰流气动特性随扰流片外形的变化关系,以期为该类修正弹的工程研制提供理论基础。
1 物理模型与数值方法
1.1 物理模型
本文所取的物理模型为某155 mm旋转稳定弹,该弹丸没有尾翼,其气动压心位于质心之前,采用陀螺稳定方式。在发射时通过弹带挤压、膛线导转获得较高的初始转速,在弹道初始段陀螺稳定因子不断上升,直至弹道末端都具备良好的飞行稳定性。而正是其稳定方式使得以旋转稳定弹为平台的弹药智能化、制导化改造相比依靠尾翼稳定的弹药更加复杂。现通过在弹丸尾部加装扰流片机构的方式使其获得气动控制,从而使旋转稳定弹具备二维弹道修正功能,如图1所示。弹丸未发射时,扰流片收纳在后体组件的控制舱内,全弹外表和普通旋转弹无异。弹丸发射后,前、后体可差动旋转,前体高旋以保持全弹陀螺稳定;后体组件中装有反旋电机可实现低旋或相对静止,由于后体质量占全弹质量比例较小,不影响陀螺稳定性。在控制指令作用下,微型扰流片可适时弹出控制舱。
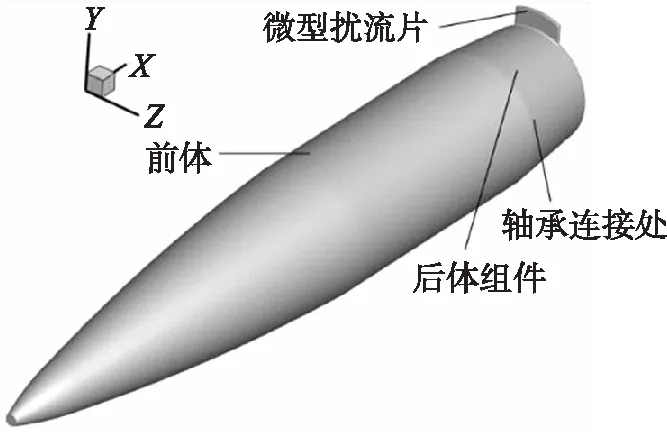
图1 带微型扰流片旋转弹的物理模型
1.2 数值模拟方法
本文基于三维雷诺平均方程,采用可实现的k-ε湍流模型,对带微型扰流片旋转稳定弹的流场进行数值模拟。数值计算域分为外层固定区、前体弹身区和后体扰流区,都为六面体结构化网格。因计算的马赫数区间包含亚声速,令弹体直径为D,则远场区域前方为20D,径向和远场后方为45D,满足亚声速压力远场边界足够远的要求[13]。图2为弹丸表面的前、后体合并网格以及后体区边界网格示意图。
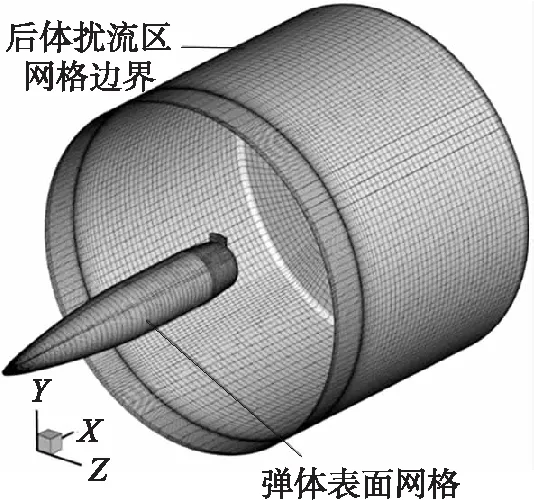
图2 部分计算网格示意图
图2中,外层固定区边界较远,故不显示。对弹丸弹头、弹身折转和后体扰流片等区域的网格都进行了加密,经多次计算达网格收敛后,整个区域网格数量约为450万。
弹体表面为无滑移壁面边界条件,壁面附近区域用标准壁面函数,其优点为在有效计算类雷诺应力条件下缓解网格细密程度,外部网格的外边界采用压力远场边界条件。本文重点关注扰流片在亚、跨及超声速下对弹丸轴向力、法向力和静力矩的影响,不考虑马格努斯力矩,并采用定常计算。
2 气动参数模型及外形设计
2.1 相关气动参数分析
弹丸无控飞行时,扰流片位于弹体内部,弹丸整体外形为轴对称。本文考虑如下3种气动力:轴向力Fa、法向力Fn和静力矩M,对应的轴向力系数、法向力系数和静力矩系数分别为CFa,CFn以及CM[14]。当扰流片伸出弹体后,气动外形不对称使弹箭所受气动力发生改变,产生的附加增量分别表示为ΔFa,ΔFn,ΔM,分别对应扰流片轴向力系数CFa,c、扰流片法向力系数CFn,c和扰流片静力矩系数CM,c,上述气动力变化量与扰流片各气动系数的关系如下:
ΔFa=q∞SCFa,c, ΔFn=q∞SCFn,c, ΔM=q∞SDCM,c
(1)
式中:q∞为来流动压(q∞=ρv2/2,ρ为空气密度,v为弹丸速度),S为特征面积。
ΔFn和ΔM本质上就是由扰流片产生的控制力和控制力矩。此时即使攻角δ=0°,仍有法向力和静力矩,只有当攻角为δM0时静力矩才为0,攻角为δFn0时法向力才为0,其中δM0,δFn0为附加力矩和附加力的气动偏心角。对于本文研究的该类气动非对称弹,δM0≠δFn0,且两者符号相反。
由于弹体任何部位的受力都可以等效到质心位置,故可用CFn,c,CM,c的符号和大小描述弹体飞行中所受控制力的方向和大小变化。如图3所示(图中X轴为弹丸速度方向,Y轴为静力矩的反方向,Z轴与X轴、Y轴构成右手坐标系),当扰流片向下打开时,扰流产生的控制力靠近弹底且指向Z轴正向,则CFn,c>0,CM,c<0。由于旋转弹的压心位于质心之前,只有当攻角增大到图示δM0位置时,静力矩才为0,而此时由于CFn,c>0,附加控制力方向与弹体所受法向力方向一致,此时法向力并不为0,存在法向力的叠加效应。
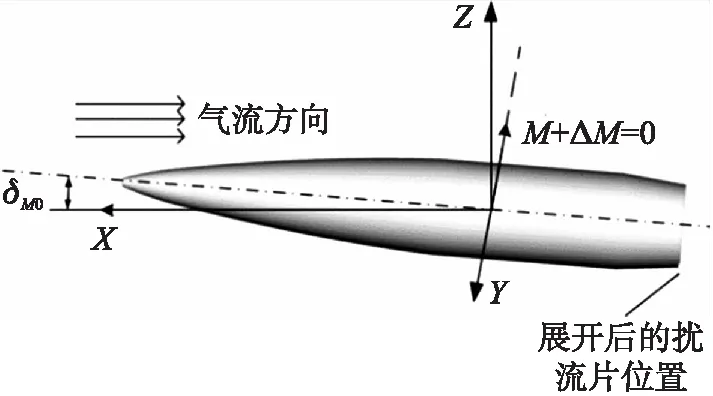
图3 带微型扰流片旋转弹所受气动力示意图
假设在扰流片作用下形成动态平衡时有如下关系式:
q∞SDC′MδM0+ΔM=0
(2)
式中:C′M为对攻角的导数。
若已知控制力矩ΔM和C′M,由式(2)及式(1)可得平衡攻角大小:
δM0=-CM,c/C′M
(3)
进而有全弹升力的表达式:
Fn=q∞S(C′FnδM0+CFn,c)
(4)
式中:C′Fn为无控弹的法向力系数导数。可见全弹的法向力大小与气动偏心角δFn0无关,只与平衡攻角δM0以及附加法向力和力矩有关,即和CM,c,CFn,c有关。因此,本文关注不同扰流片外形参数、不同马赫数对应的CM,c,CFn,c。
2.2 外形设计
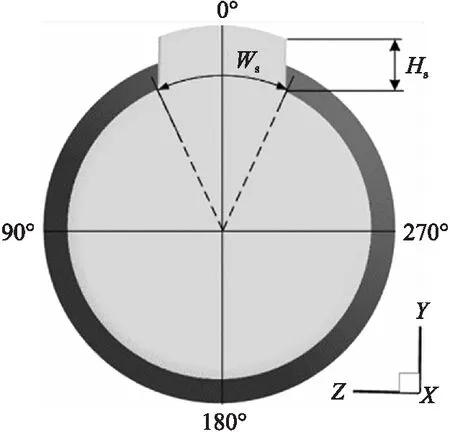
图4 外形参数描述及计算坐标系示意图
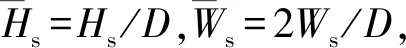
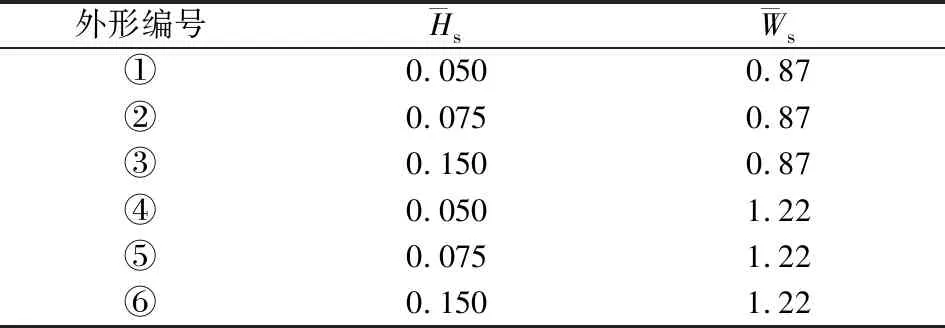
表1 扰流片气动外形参数取值表
考虑尽可能增大扰流控制机构的操纵性,本文将扰流片布置于弹丸尾部[15]。由于该弹飞行马赫数范围较大,为全面分析扰流片的影响,选取Ma=0.5~1.5,攻角δ=0°,4°。
2.3 扰流性能函数
为对不同扰流外形的气动特性进行评估分析,并期望寻求较优的扰流片结构参数,需要建立扰流片性能函数。当仅考虑由于扰流产生的附加法向力和附加轴向力时,可将两者之比作为性能函数:
(5)
而文献[3]考虑附加轴向力尽可能小而附加力矩尽量大,得出的性能函数为
(6)
为了深入研究扰流片所引起的气动干扰对全弹的影响,本文考虑带微型扰流片旋转稳定弹全弹的升阻比,构造如下性能函数:
(7)
式中:CD0,CD2分别为无扰流片时的零升阻力系数和诱导阻力系数。将式(3)代入式(7),得:
(8)
3 数值模拟结果与分析
为分析扰流片外形参数对扰流性能的影响,采取控制变量法,分析在马赫数、攻角一定时扰流情形随气动外形参数的变化,流场分析时主要选取Ma=1.5,0.95,0.8,δ=0°。由于δ=4°时流场情形与δ=0°时差别不大,仅在后文做补充讨论。
3.1 扰流后体区的压力分布
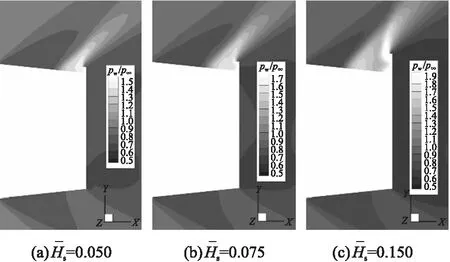
图5 Ma=1.5时扰流区纵向截面压力云图
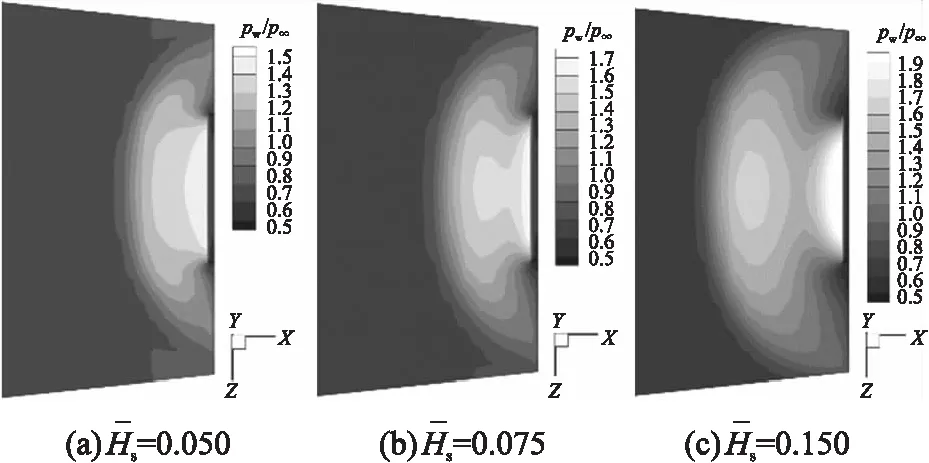
图6 Ma=1.5时扰流区弹体表面压力云图
由图5和图6可见,在超声速条件下扰流片的存在使弹尾局部产生了剧烈的压力变化,扰流片迎风表面压力最大,且靠近扰流片前方的区域压力也较大;扰流产生的马赫波系在弹体表面呈类似半椭圆形分布,随着马赫波系距离扰流片越来越远,相应位置的弹体表面压力逐渐降低。
从左至右观察图5和图6,随着扰流片高度的增加,扰流片表面以及靠近扰流片的弹体表面处的压力最大值增加,扰流片前方压力梯度区域不断扩大;当扰流片高度超过一定值后,扰流片表面压力随高度方向出现波动,扰流片上方以及靠近弹体表面的下方产生了2个高压区,并且前方弹体表面区域也产生了一个压力最大值较低的副高压区(与脱体激波类似),副高压区将扰流片产生的压力影响区域扩大。因此,扰流片高度越大,弹体表面压力影响区域相应越大。
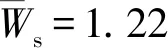
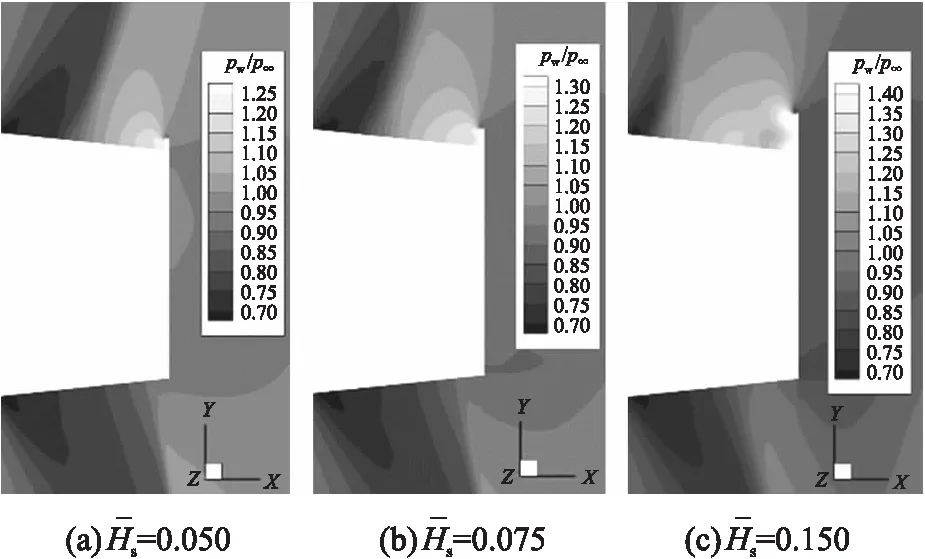
图7 Ma=0.95时扰流区纵向截面压力云图
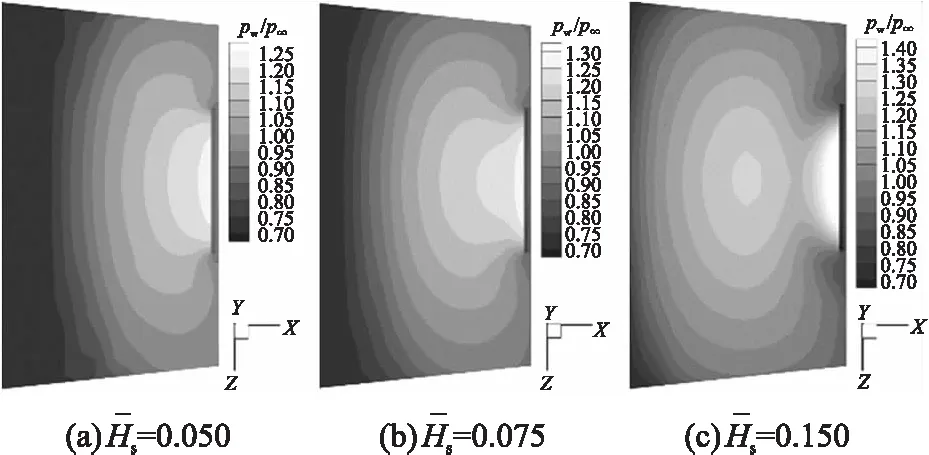
图8 Ma=0.95时扰流区弹体表面压力云图

图10 Ma=0.8时扰流区弹体表面压力云图
图11~图13分别为不同马赫数条件下采用不同扰流片高度时不同X截面的弹体表面压力系数pw/p∞分布的对比。
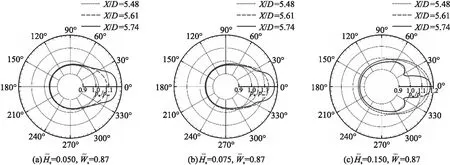
图11 Ma=0.8时不同X截面的压力分布
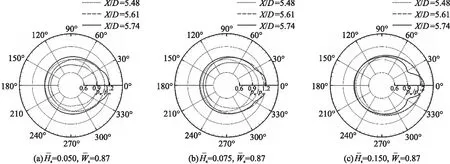
图12 Ma=0.95时不同X截面的压力分布
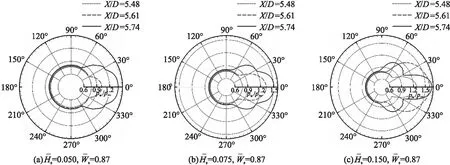
图13 Ma=1.5时不同X截面的压力分布
由图可见,在对称面两侧压力分布对称,同一截面沿周向压力分布θ=0°处最大,且越靠近扰流片压力基本呈增加趋势;任一截面θ∈(90°,270°)时,压力最低且几乎不变;靠近扰流片近处的周向压力变化较剧烈,亚、跨声速下扰流片达到一定高度后出现压力副峰值,而超声速下即使扰流片高度较小,沿周向的压力变化也具有较高波动。
综上所述,在亚、跨和超声速条件下,扰流片均具有改变弹尾压力分布的能力,且超声速下其扰动性能更为明显,弹尾的周向压力变化更为剧烈。
3.2 扰流气动特性分析
为了定量描述不同外形扰流片引起的压力效应,从3.1节的数值模拟结果中提取各气动系数,列于表2~表4,其中,表2为不同外形尺寸对应的扰流气动系数,表3和表4为外形参数改变引起的扰流气动系数增量。
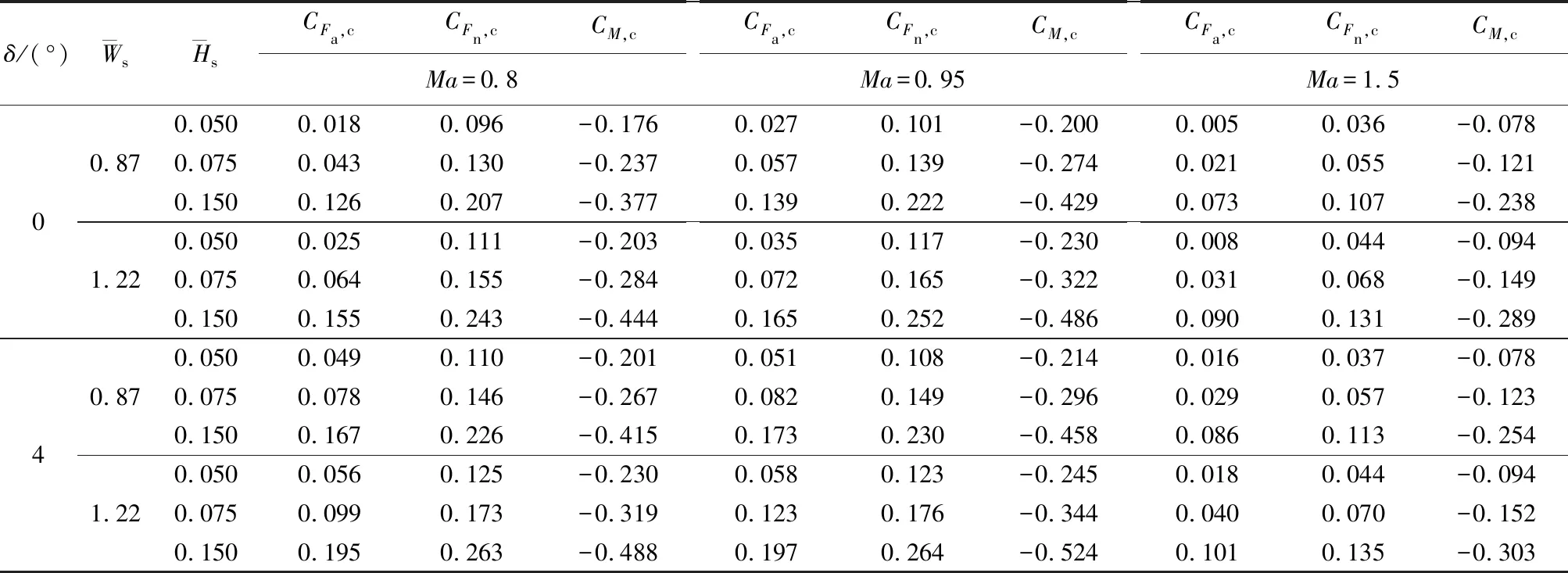
表2 扰流气动系数计算结果
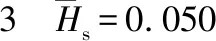
表时扰流片高度变化引起的各气动系数增量
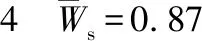
表时扰流片弧长变化引起的各气动系数增量

为便于描述改变外形参量提高控制力和控制力矩的效果,定义增加单位面积引起的控制力和控制力矩增量百分比分别为EFn,EM,计算公式如下:
(9)
式中:Sb,Sa分别为原外形和外形变化后对应的扰流片面积;CFn,c|Sb,CM,c|Sb分别为原外形的扰流片法向力系数和静力矩系数;CFn,c|Sa,CM,c|Sa分别为外形变化后的扰流片法向力系数和静力矩系数。因EFn和EM强相关(计算值十分接近),下文以讨论EFn为主。
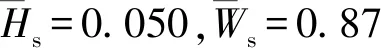
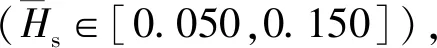
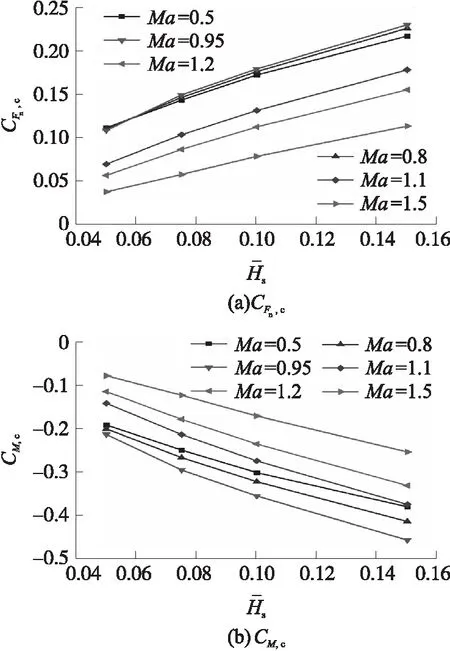
图14 CFn,c和CM,c随的变化曲线
图15给出了不同扰流片尺寸时的全弹法向力系数CFn和静力矩系数CM随马赫数的变化(δ=4°),同时与不带扰流片的情况进行了对比,图中,外形编号对应的扰流片尺寸见表1。
由图15可知,带扰流片的全弹法向力系数远大于无扰流片时,且低马赫数时的增加量相对较大,并且全弹静力矩系数的改变量较大。结合2.1节可知,其改变弹体姿态的能力也较好,因此扰流片在Ma为0.5~1.5的范围内都具有良好的控制效果。
以上主要考察了气动力系数CFn,c,CM,c随扰流片几何外形的变化,为结合扰流片轴向力系数分析外形变化对扰流性能的影响,根据2.3节公式给出各性能函数的值,其随扰流片结构参数的变化情况如图16所示,图中给出了Ma=1.5时Jr1,Jr2的指数拟合曲线,以便更好地观察其变化趋势。表5给出了计算Jr3所需的气动系数CD0,CD2,C′M及C′Fn,这些系数是对无控弹数值计算得到的。
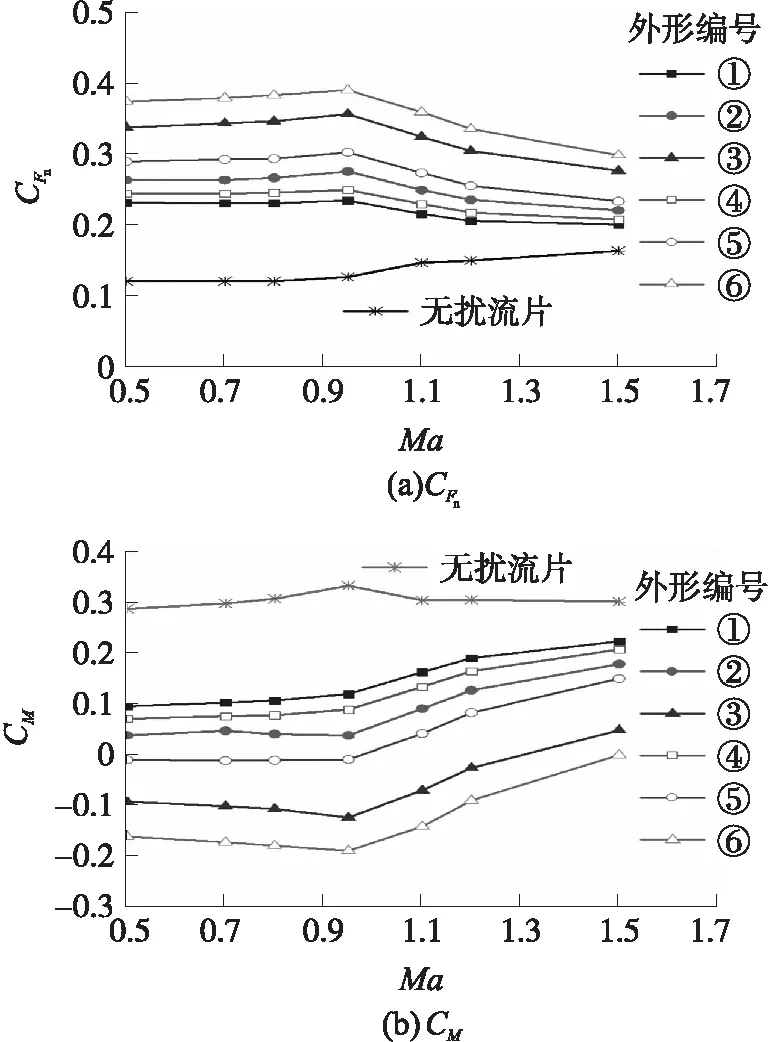
图15 CFn和CM随Ma的变化曲线
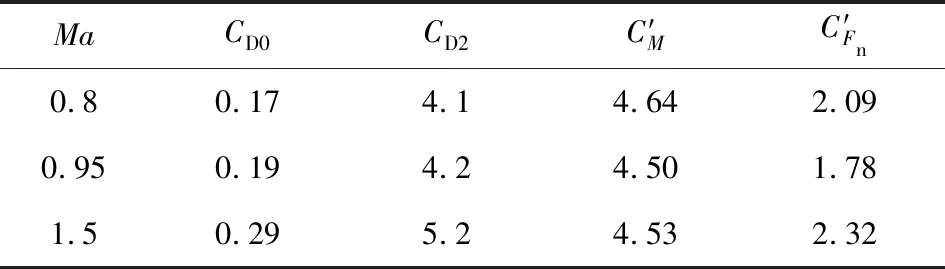
表5 计算Jr3所需的无控弹气动系数
综上分析,对于同一外形扰流片,Jr3在Ma=0.95时最大,Ma=1.5时最小,且各性能函数都在Ma=1.5时变化最大;增加同等单位面积的条件下,倾向于选择增加扰流片高度,并且在超声速下增加高度的效果更明显;随着高度增加,单位面积增加的扰流效果逐渐降低,Jr3上升趋势减慢,Jr1和Jr2数值减小并趋于稳定。可见,增大扰流效果必将导致Jr1和Jr2数值的下降。
采用旋转稳定方式的弹药,因没有大面积尾翼或弹翼,本身不可能产生较大的升力,故其升阻比不高,但采用扰流片布局方式的控制作用力远离全弹气动压心,能够有效改变弹体姿态。因此带微型扰流片旋转稳定弹今后的发展方向仍以远距离作战打击的二维修正弹为主,可以发挥其末端弹道修正,降低射击误差,提高打击精度的主要功能,同时其升阻比上限较低的特性不会对其主要功能产生较大影响。
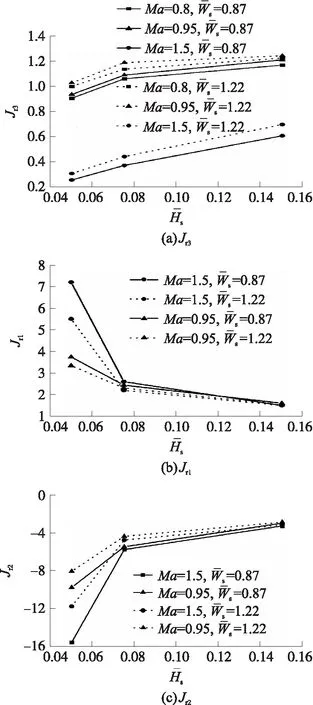
图16 性能函数随扰流片高度的变化
4 结论
本文以带微型扰流片的旋转稳定弹为研究对象,采用计算流体力学方法,数值模拟了不同来流条件下该类旋转稳定修正弹的流场,研究了扰流片高度和弧长变化对扰流片表面以及靠近扰流区域弹体表面压力分布的影响,得到如下结论:
①扰流片位于弹体尾部时产生的气动控制效应明显,其附加气动力作用方向与弹体攻角姿态调整方向相同,并随着攻角增大其扰流效果有所提升。
②扰流片法向力系数CFn,c和扰流片静力矩系数CM,c与扰流片高度呈良好的线性关系,且在超声速下的线性度比亚跨声速下更好。
③增加扰流片高度产生的单位面积扰流效果要优于增加扰流片弧长产生的效果,实际研制过程中可通过生产不同高度的扰流片来调整控制力的大小。
