基于变形热的NEPE推进剂本构模型
2020-10-09宋峻
宋 峻
(中国船舶726研究所,上海 200025)
目前,固体火箭被广泛地运用到火箭弹、战术火箭武器和运载火箭助推中。通常,火箭武器在发射过程中都会承受很大的轴向过载,这对于固体推进剂药柱的结构完整性是一个巨大的挑战。然而,固体火箭发动机中药柱在发射过程中的结构完整性是固体火箭发动机正常工作的前提。为了准确分析固体推进剂药柱在高应变率下的结构完整性,需要了解推进剂在高应变率下的力学特性和建立准确的本构模型。因此,众多研究者通过分离式霍普金森装置(split Hopkinson pressure bar,SHPB)研究固体推进剂在高应变率下的力学特性[1-4]。
在进行SHPB实验中,固体推进剂材料试件在受到入射杆撞击后,固体推进剂试件有明显的发热现象。多次实验中,触摸推进剂试件表面,都会感觉到明显的温度升高,这说明这种现象并不是偶然发生的,然而却很少有研究人员对此现象进行解释和分析。“变形热效应”理论可以很好地用于解释固体推进剂材料在SHPB实验中的温升现象。非理想弹性材料受到外力的作用时会发生变形,外力会做不可回复的塑性功,塑性功会以热能的方式释放出来,从而改变材料内部温度。在材料变形程度很大或者变形速度极快的情况下,材料内部的温度改变会非常明显,这就是“变形生热效应”。固体推进剂是一种典型的黏弹性材料,在冲击载荷下,固体推进剂材料变形速率极快,会迅速将试件压溃,所以冲击过程对推进剂试件所做的功造成的变形是无法回复的。发生这一过程的时间又极短,这样便造成生成热的速率远大于流失热的速率,可以近似于绝热过程,由此便会导致固体推进剂材料自身温度急剧升高,固体推进剂材料表面会表现出发热现象[5]。
大多数研究人员在研究材料动态力学本构模型时,对于SHPB等高应变率实验没有考虑材料温升对材料力学响应的影响,认为材料变形中的温度场是稳态的(即材料内部温度与外界环境温度一致)[6-7]。固体推进剂是属于典型的黏弹性材料,冲击变形过程中的外力做的功所引起的温升对固体推进剂力学性能有显著的软化作用。在高应变率加载下,实验时间非常短,短时间的热流失可以忽略,由此得到的应力-应变曲线可以认为是绝热曲线,且随着应变率的升高,材料的温升也会随着升高[8],温升产生的软化效应对固体推进剂力学响应的影响势必更加明显。因此,固体推进剂的动态本构模型还应该考虑固体推进剂在高应变率下的变形温升对其力学性能的影响,这样才能准确地描述固体推进剂在高应变率下的动态力学响应。
1 考虑变形生热的本构模型
1.1 黏-超弹本构模型的建立
由以往的研究可知,固体推进剂具有明显的黏弹特性,又具有较大的变形。这种力学特性常常不能通过黏弹性本构模型进行准确的描述,因此,研究人员引入超弹性本构模型与黏弹性模型结合,从而构建黏-超弹本构模型来描述固体推进剂在高应变率下的力学行为。对于固体推进剂黏弹性模型,具有2个Maxwell单元的朱王唐(ZWT)模型[9]被研究人员广泛应用,因为它是一种可以表示高应变率和低应变率下材料力学行为的非线性黏弹性本构模型,其一维形式如下:

(1)
式中:右边第一项fe(ε)=E0ε+aε2+bε3,为非线弹性平衡响应单元,其中,E0,a,b为对应的弹性常数,ε为应变;第一个积分项表示材料在低应变率下的黏弹性响应,第二个积分项表示材料在高应变率下的黏弹性响应;E1,E2分别为低频Maxwell单元和高频Maxwell单元的弹性常数;τ1,τ2分别为低频Maxwell单元和高频Maxwell单元的松弛时间。
在高应变率加载条件下,由于实验时间非常短,远小于低频Maxwell单元中的松弛响应时间,因此,在高应变率加载实验中,低频Maxwell单元可以被近似为弹性常数为E1的简单弹簧,则式(1)可以简化为

(2)
式中:σe(ε)=fe(ε)+E1(ε),为非线弹性平衡响应。
为了描述NEPE推进剂大变形的特性,需要对ZWT本构模型进行修正,将其非线弹性体部分替换为一个超弹响应单元。选择两参数的Mooney-Rivlin[10]超弹模型代替非线性弹性项σe(ε),即
(3)

λ=1-εeng
(4)
将上述的超弹响应部分式(3)和ZWT高频响应单元式(2)结合,即构成黏-超弹本构模型:
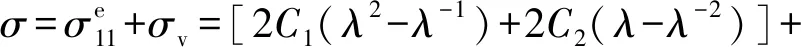
(5)

1.2 冲击生热计算方法
根据热传导理论,应变和温度之间的关系可以表示为
(6)
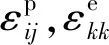
(7)
对式(7)积分,可以得到温升表达式:
(8)
固体推进剂试件在变形中所做的功都转化为热,即取β=1[5],由此变形生热计算公式为
(9)
由于不能准确确定NEPE推进剂在高应变率下的屈服点,且如果对弹性和塑性分段也会导致本构模型的分段,增加了复杂程度。因此,采用式(9)计算NEPE推进剂材料在高应变率加载下的温升将存在一定程度的困难,为了计算的简单,需要对式(9)的计算方法进行一定程度的简化。在高应变率压缩实验中,NEPE推进剂的初始弹性段应变相对于总应变来说所占的比例很小,而且这一段初始弹性应变相对应的应力值也相对较小。因此这里为了计算的简单,采用不区分弹性与塑性阶段的方法,用整个应变段的积分结果来计算温升,最终可以得到NEPE推进剂材料冲击加载变形生热温升理论计算公式[5]:
(10)
1.3 考虑变形生热的本构模型
为了准确表述在冲击加载下固体推进剂变形引起的温度升高对固体推进剂力学行为造成的软化影响,参照J-C模型中考虑温度的形式,本文引入热软化函数f(T)对式(5)所示的黏-超弹模型进行修正,即σtrue,T=f(T)σtrue,其中,σtrue,T表示考虑温升影响的真实应力。软化函数f(T)的形式表示为
f(T)=1-T*m
(11)
式中:m为试件材料的热软化系数,T*为无量纲化的温度项,即T*=ΔT/T0,T0为冲击加载实验初始温度,本文实验初始温度为293.15 K。
2 NEPE推进剂SHPB实验
图1为分离式霍普金森实验装置,主要包括高压气炮、子弹杆、入射杆和透射杆等。分离式霍普金森压杆装置的实验原理为[12]:首先,利用空气压缩机往前端的高压气炮中充入高压气体,高压气体推动子弹杆加速。然后,子弹杆以一定的初始速度冲出炮口与入射杆撞击,给予入射杆一定的冲击能量,在入射杆的被撞击端产生压缩波。最后,入射杆也以一定速度撞击固体推进剂试件。由于入射杆和固体推进剂2种材料的横截面以及阻抗不同,压缩波在两者的接触面既会发生透射现象又会发生反射现象,其中小部分压缩波会反射形成反射波返回到入射杆中,剩下的压缩波信号则会穿过固体推进剂进入透射杆中形成透射波。如果在入射杆和透射杆中分别贴上半导体应变片,便可以测量到入射杆上的入射波信号和反射波信号以及透射杆上的透射波信号。对测试系统得到的信号,采用Matlab程序进行处理,即可获得固体推进剂材料在高应变率压缩加载条件下的真实应力-工程应变曲线。调节输入高压气炮中的压力,可以获得不同高应变率下固体推进剂的压缩力学响应。

图1 SHPB试验装置实物图
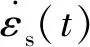
(12)
(13)
(14)
式中:c0为杆中弹性波速;L0为试样的原始长度;A,As分别为入射杆和推进剂试件的横截面积;E3为压杆的弹性模量;εr(t),εt(t)分别为反射波、透射波的应变值。
为了验证SHPB实验的有效性,需要检测试件两侧的应力是否平衡。图2给出了通过“二波法”获取的理论投射应变和实验结果的对比曲线,可以看出理论计算结果与实验测试结果基本吻合,这说明实验中试件两端的应力基本相当,因而实验结果是可靠的。
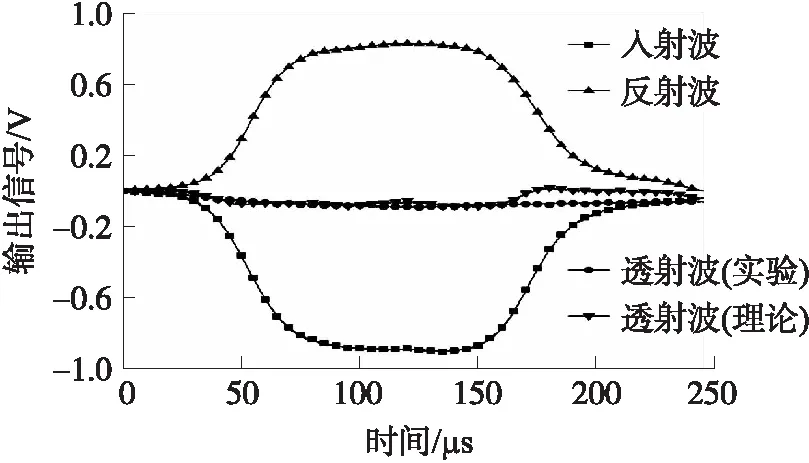
图2 应力平衡检验结果
NEPE推进剂试件尺寸如图3所示,其中管状试件的外径2r1=10 mm,内径2r2=3 mm,固体推进剂试件长度L=2.5 mm。调节输入气炮的压力,可以得到1500 s-1,2 500 s-1,3 500 s-1,4 500 s-14个应变率下NEPE推进剂真实应力-工程应变曲线。对于同一应变率加载条件,获取3组有效实验数据,最后取平均值,实验结果如图4所示。
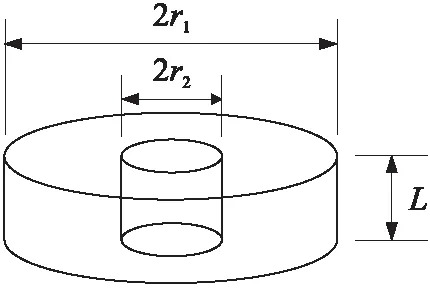
图3 NEPE推进剂试件示意图
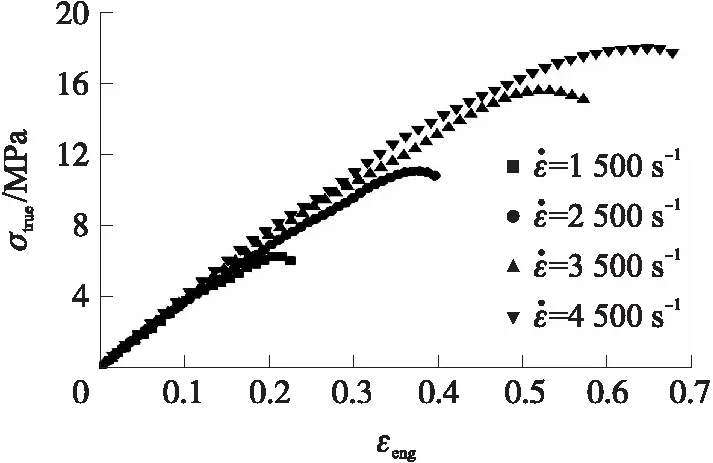
图4 NEPE推进剂压缩真实应力-工程应变曲线
3 本构模型参数确定及验证
3.1 温升函数的拟合


图5 不同应变率下温升函数拟合结果
3.2 本构模型材料参数的确定
对黏-超弹本构模型参数的确定,仍然利用1 500 s-1,2 500 s-1,3 500 s-1实验结果,取C1=8.20,C2=-1.025 6,E2=84.859 6,τ2=0.000 45和m=2.728 9,拟合结果如图6所示。

图6 实验曲线拟合结果
3.3 本构模型的验证
根据前文参数结果,得到考虑变形生热的黏-超弹本构模型的具体形式:
将4 500 s-1的实验数据代入到本构模型中,得到理论预测曲线,与实验曲线的对比结果如图7所示,可以发现该模型的预测效果很好,可以很好地反映NEPE推进剂在变形较大时的软化情况。
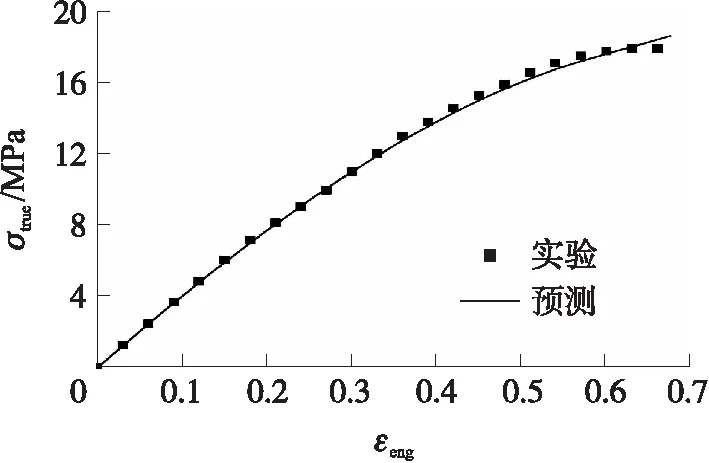
图7 考虑变形生热的黏-超弹本构模型预测曲线与实验曲线的对比
4 结论
通过冲击载荷下的理论温升计算方法,得到了不同应变率和应变下的理论温升曲线,并将其拟合为应变相关和应变率相关的经验函数代入到本构模型中。利用NEPE推进剂的SHPB实验数据,获取了黏-超弹本构模型参数,最后利用4 500 s-1实验数据对该模型进行了验证,结果表明,该模型可以很好地预测NEPE推进剂在冲击载荷下较大应变时的软化现象,这表明在研究聚合物冲击载荷条件下本构模型时应该考虑冲击生热对聚合物造成的软化影响。
