弹体穿越冰水混合物流动过程的数值模拟

张 军,蔡晓伟,宣建明,王英霖

(1.南京航空航天大学 航空学院 非定常空气动力学与流动控制工业和信息化部重点实验室,江苏 南京 210016;2.中国船舶科学研究中心 水动力学重点实验室,江苏 无锡 214082;3.南京理工大学 能源与动力工程学院,江苏 南京 210094)

潜射导弹作为一种可以进行水下发射的武器系统,具有射程远、速度快、反应时间短、命中精度高、隐蔽性强等诸多优点,具有重要的军事与战略意义[1-2]。在高纬度以及部分中纬度海域,如我国黄海、渤海部分海域,由于气候的原因,存在着一定时间的冰期[3]。海面具有大面积的冰体覆盖,可以进一步提高潜射导弹发射的隐蔽性与突然性。

国内外均已开展了水下发射导弹出水过程的数值与试验研究[4-7],但对于细长导弹穿越冰水混合物出水过程的研究较少,其流场的变化比单纯的出水过程更加剧烈,成为导弹冰下发射成功与否的关键因素之一。ANSYS/LS-DYNA软件基于有限元算法,对流固耦合问题具有良好的适应性[8-9]。本文利用ANSYS/LS-DYNA有限元分析软件,对细长弹体穿越冰水混合区域出水过程进行数值模拟研究,获得这一过程中流场的变化规律以及弹体质心位移变化等结果,研究成果可以为导弹冰下发射研究提供技术支持。

1 数值模型

1.1 数值方法

采用ALE算法[10],先执行一个或者几个Lagrange时间步计算;当单元网格产生变形之后,再执行ALE时间步计算,对内部单元进行网格重新划分,将变形网格中的单元变量和节点矢量值插值到重新划分后的网格中。基于ALE方法,在LS-DYNA中可以方便地将Euler网格与Lagrange网格进行耦合,以处理流体与结构之间的相互作用问题。本文采用此方法进行弹体穿越冰水气混合物流场的数值模拟研究。

采用流固耦合算法时,通常需要对Lagrange结构进行约束,将结构的相关参量传递给流体单元。本文采用罚函数约束[11]的方法进行耦合计算,罚函数耦合系数考虑拉格朗日节点(弹体,即从物质)和欧拉流体(水与空气,即主物质)之间的相对位移。检查每一个节点对主物质表面的贯穿,如果从节点不出现贯穿,就不进行任何操作;如果发生从节点对主节点的贯穿,界面力F就分布到欧拉流体的节点上。

1.2 材料模型与状态方程

流体区域包含水与空气2种流体介质,水与空气采用NULL材料模型,水介质的状态方程采用Gruneisen状态方程:

(1)

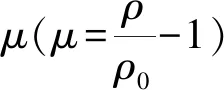
空气介质采用线性多项式状态方程:

p=C0+C1θ+C2θ2+C3θ3+(C4+C5θ+C6θ2)E

(2)

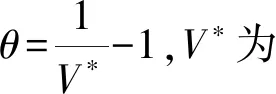
对于弹体,在出水的过程中,弹体的变形量很小,为了加快运算的速度,减少计算时间,将弹体作为刚体处理,弹体的材料模型选择RIGID模型。表1给出了冰体材料参数,水、空气、弹体、冰体对应的材料模型与状态方程[12]如表2所示。

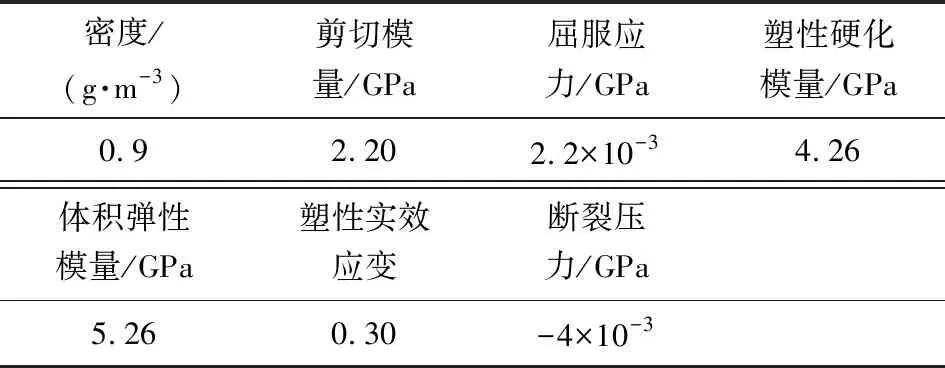
表1 冰体材料参数

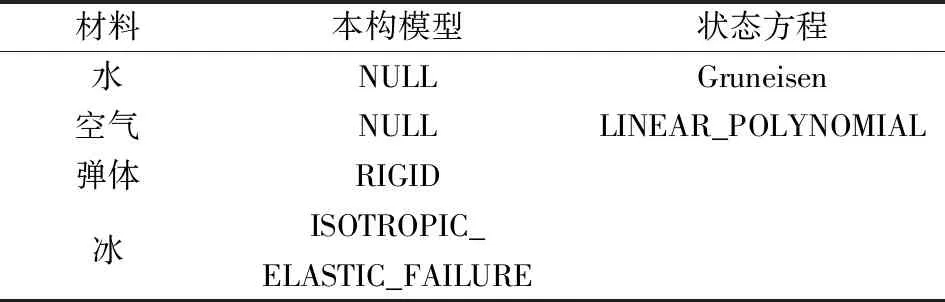
表2 材料模型与状态方程

2 计算模型

计算模型包括细长弹体(见图1)、冰体,以及由空气域和水域组成的流体区域,弹体的底部直径为118 mm,弹体长1 247 mm(质心距离头部顶点676.12 mm),弹体材质为铝合金,壳体厚度为5 mm。由于本文主要关注的是流场的变化以及弹体的运动姿态,因此忽略弹体的变形,将弹体作为刚体进行模拟计算,弹体采用Lagrange单元。弹体的初始速度为20 m/s,运动方向为竖直向上,攻角为0°;初始时刻,弹的运动方向和z轴正方向重合。所建立的三维有限元网格模型如图2所示。

图1 弹体外形侧视图

图2 弹体出水网格模型

3 数值模拟状态及结果分析

冰体的分布方式以及弹体相对位置对出水过程存在一定的影响,本文研究了3种不同的分布方式(规则分布、菱形分布、随机分布,见图3)及2种不同的相对位置(冰体正下方和冰体间隙)对质心运动轨迹的影响,共有6种计算工况,具体工况定义见表3。

图3 冰体分布方式

对于以上6种不同工况,细长弹体穿越冰水混合区域出水时,弹体质心在x、y2个方向上的位移如图4所示。表4给出了t=1 s时,弹体质心位移。从计算结果可以发现,弹体的初始相对位置对弹体出水后x方向质心位移影响最大,弹体从冰体间隙之间出水相较于弹体从冰体正下方出水,在x方向上的偏移要大数倍至数百倍。在同样的冰体分布方式下,弹体质心在y方向上的位移同样受到相对位置的影响,弹体从冰体间隙之间出水时,在y方向上的位移要明显小于从冰体正下方出水时的位移。相对位置相同、冰体分布方式不同时,弹体质心在x方向位移差距不大,但是弹体质心在y方向位移存在着较大的偏差。

表3 计算工况条件定义

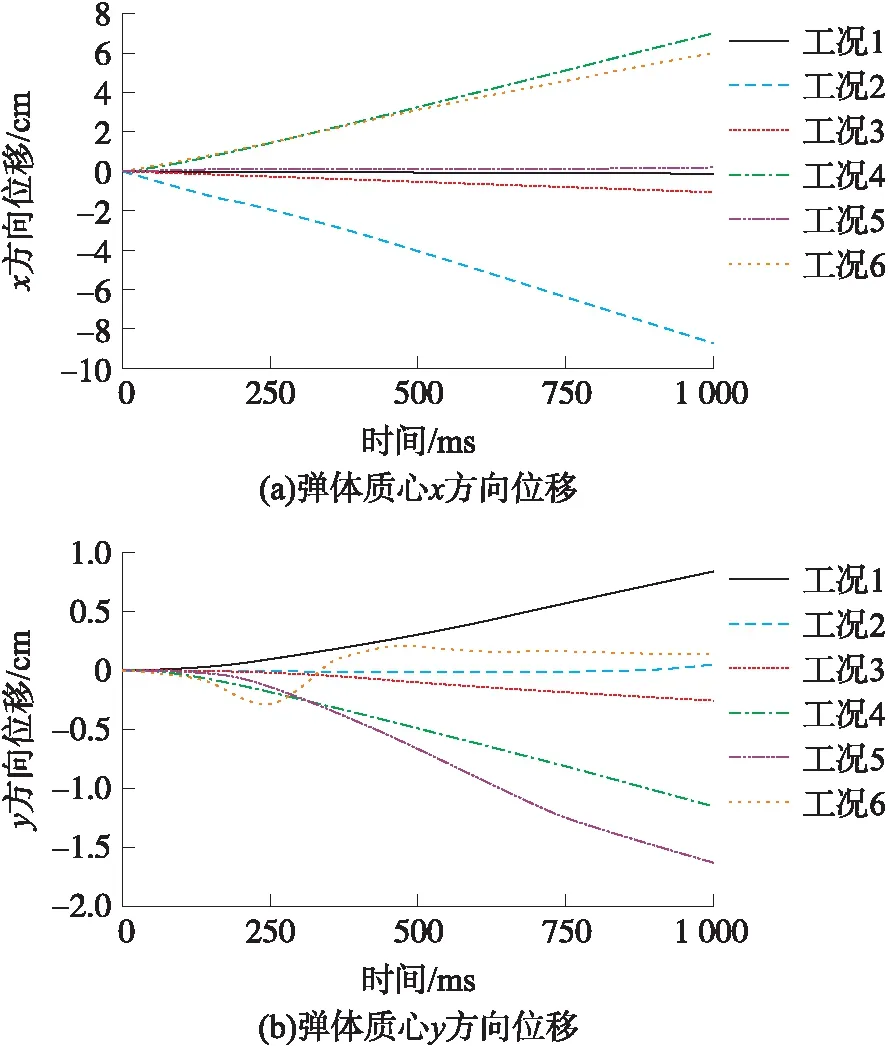
图4 6种工况下弹体质心位移

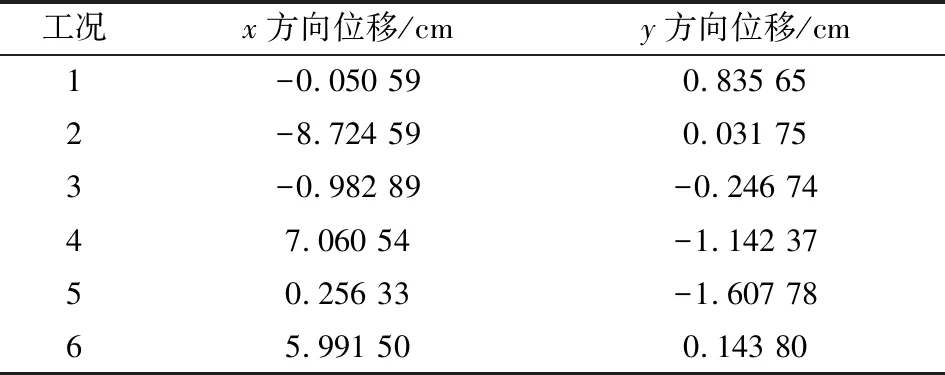
表4 t=1 s时弹体质心的位移

对工况1进行深入的流场结果分析,图5～图10给出了具体的流场云图和速度随时间变化曲线。

弹体在离开水域时(t=1 s),流场的密度等值线图如图5所示,从图中可以看出,弹体在穿越冰水混合区域后,水域流场中密度的等值线在各个方向上均有分布。弹体在出水时,水域与空气域界面上,围绕弹体周围的密度等值线分布较为密集,说明此位置流体的密度梯度较大,变化较为剧烈。随着到水-气界面距离的增加,水域中的密度等值线变得稀少,同时水域流场的四周出现了因为空泡而形成的密集等值线圆环。浮在水面的冰体受水与弹体的作用,位置发生改变,位于弹体正上方的冰体被推离出水面,同时出现较大程度的破碎。

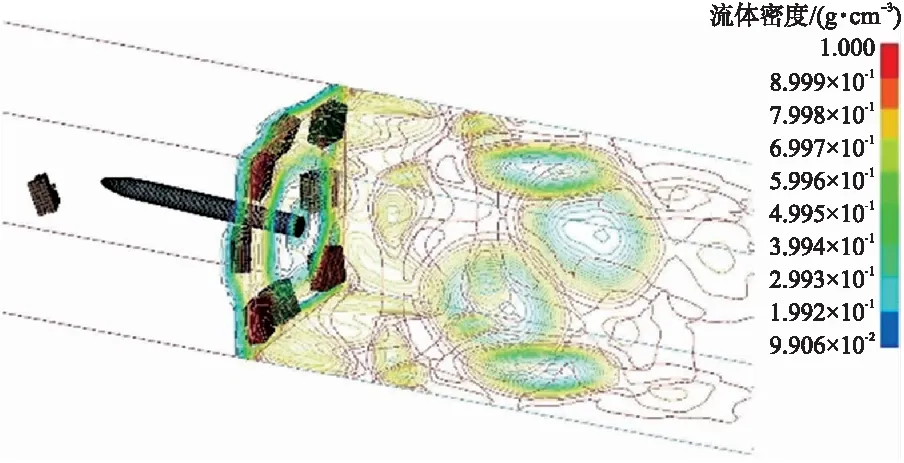
图5 流场密度等值线图

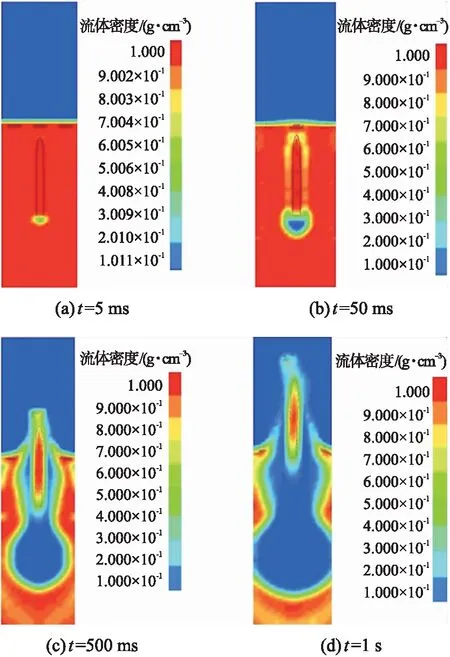
图6 流体密度变化云图

为了更清楚地分析弹体出水过程,选取4个时间节点,获得截面的流场属性云图,见图6～图9。

截面上的流体密度云图如图6所示。从图中可以发现:在t=5 ms时,如图6(a)所示,在弹体的底部,流体的密度开始变小,出现了空化的现象;随着弹体的运动,当t=50 ms时,如图6(b)所示,随着弹体在水中的运动,弹底部空泡体积逐步增大,弹体侧面也出现了空化现象;随着时间的进一步推进,弹体周围空化现象加剧,使得弹体侧面与弹底的空泡连成一体,如图6(c)所示;当弹体出水时,部分的水被带入空气中,如图6(d)所示。

弹体出水过程中的流场应力云图如图7所示。从图中可以看到:当t=5 ms时,如图7(a)所示,弹底处有较大的应力值,同时弹体侧面也有较大的应力值,但是和弹底处相比,值要小一些;随着弹体的运动,流场出现较大应力值的范围逐渐扩大,逐步向远离弹体的区域扩散,但是应力峰值开始减小,如图7(b)所示;当t=500 ms时,弹体部分进入空气中,此时弹头以及弹体侧面与空气接触的位置出现较大的应力值,其他位置的应力值较小, 如图7(c)所示;当t=1 s时,弹体完全进入空气中,弹体周围出现了明显的高应力值,且出现了较大的应力峰值,弹后空泡区域的应力值变得极小,如图7(d)所示。

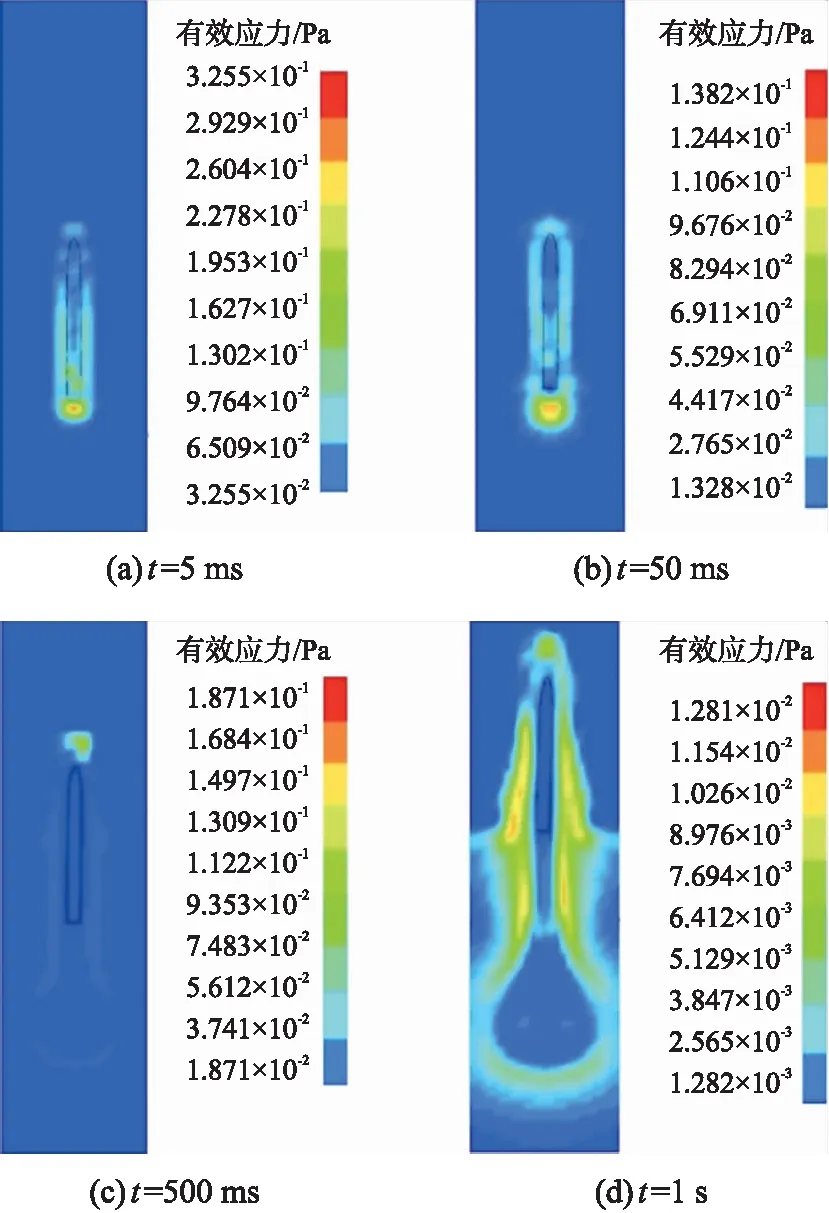
图7 流体应力变化云图

流体区域的压力云图如图8所示。从图中可以发现:在弹体运动的初期t=5 ms时,如图8(a)所示,流场中的压力主要集中在弹体所在位置且集中于弹体的后部,最大压力约为1.192 MPa;当t=50 ms时,如图8(b)所示,流场中压力集中分布的区域发生变化,最大压力值减小,约为0.268 7 MPa,当弹体还未出水时,流场中压力主要集中在弹体所在位置;当t=500 ms时,如图8(c)所示,弹体部分进入空气,空气中的压力分布较弹体在未出水前变化剧烈,最大压力位置位于弹体头部上方。由于空气阻力较水中阻力小得多,此时流场中最大压力为25.150 kPa,空气域出现部分负压区域;弹体完全出水进入空气后,流场区域的压力分布变得较为均匀,仅弹体头部附近存在最大压力为1 806 Pa的压力分布,如图8(d)所示。

图8 流体压力变化云图

冰水混合区域流场的z方向速度(即竖直向上)变化云图如图9所示。

从图9(a)中可以看出,由于受到弹体运动的影响,弹体周围的流体开始流动,流速最大的区域位于弹底部,最大速度约为13.27 m/s。当t=50 ms时,如图9(b)所示,弹体产生的扰动向远处传播,导致更大范围的流体开始流动,弹体周围的流体速度约为1.94～2.90 m/s。当弹体进入空气中后,空气受到弹体的影响开始运动,弹体上方冰体附近的空气也产生流动现象,如图9(c)所示。当弹体离开水域后,弹体附近空气的流速约为1.5 m/s,水域中的流速减小,如图9(d)所示。

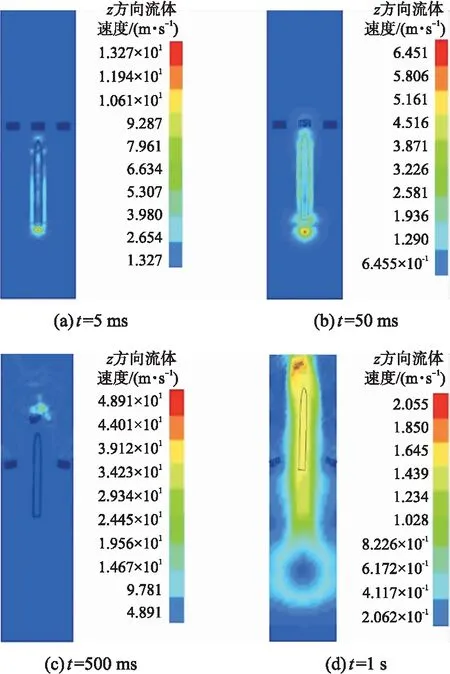
图9 流体z方向速度变化云图

在弹体出水的过程中,对弹体的速度进行一定的滤波处理,得到如图10所示的速度随时间变化曲线。从图中可以看出:在运动初始阶段,由于受到水的阻力作用,弹体的速度变化剧烈,速度从20 m/s迅速下降;随后速度出现波动,波动幅度不断减小,大约在2 ms后速度的波动幅度明显变缓,逐步接近匀速运动。

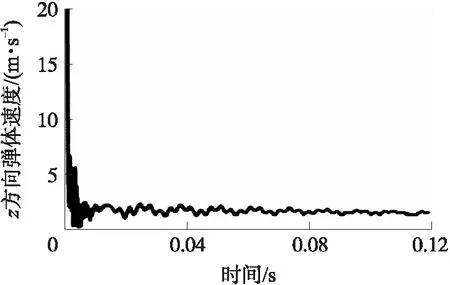
图10 弹体在z方向的速度随时间的变化曲线

4 结论

采用LS-DYNA软件,对冰下发射的导弹出水运动过程进行了数值模拟,获得如下结果:

①弹体在水下运动过程中,首先在弹底形成空泡,随着弹体的运动,空泡逐渐扩大,空化现象愈发显著。

②弹体在运动过程中,水域流场中应力主要集中于弹底以及弹体侧面,随着弹体的运动,流场存在应力的范围不断向弹体远处传播,且峰值不断减小。当弹体出水进入空气中后,弹体周围的空气流场区域存在较大的应力,但应力峰值较小。流场应力的存在对弹体的运动产生一定的影响。

③水域流场中,弹体附近流体压力出现较大的梯度,随着弹体逐渐离开水域,压力峰值不断减小。当弹体进入空气域时,最大压力位置位于弹体头部上方,弹体附近会出现部分负压区域。弹体完全出水后,水域压力分布变得较为均匀。

④弹体在出水运动时,弹体周围流体的流速较大。随着弹体的运动,流场扰动会逐渐向远离弹体的地方传播,导致更大范围的流体出现流动现象,但是速度峰值逐渐变小。当弹体进入空气中,空气受到扰动,静止的空气开始运动,弹体与冰体附近的速度值较大。弹体在运动的初期,速度骤降,随后速度降低程度变缓,最终弹体的速度趋于稳定。

⑤不同的冰体分布方式以及初始弹体相对位置,会造成弹体质心位移不同。