中心极限定理在实际中的应用

张志成，张 艳

（1.河南工学院，河南 新乡 453003；2.河南师范大学 计算机与信息工程学院，河南 新乡 453007）

0 引言

中心极限定理是概率论中重要的基本理论，在概率论及数理统计的理论研究和实际应用中都有着举足轻重的地位。关于相互独立的随机变量之和的极限分布的一系列定理统称为中心极限定理。只要n充分大，我们就可以用中心极限定理作近似计算。它为解决实际应用问题提供了理论基础。

国内外不少专家、学者广泛研究了中心极限定理在实际中的应用。2005 年唐莉等人以彩票业和保险业为实例讨论了大数定律和中心极限定理的实际应用[1]。同年，王东红研究了大数定律与中心极限定理在保险中的重要应用[2]。2011 年，王丙参等人讨论了中心极限定理在制定保费及自留额、拟定保险单位数及减少保险个人平均危险值等方面的应用[3]。2018 拉穷等探讨和分析了中心极限定理在保险经营中的应用[4]。本文从概率预测和样本容量推断两个方面来探讨中心极限定理在实际生活中的应用。

1 中心极限定理

棣莫佛-拉普拉斯中心极限定理[5]：

中心极限定理表明，如果某一个量的变化受到许多随机因素的影响，且这些因素中每一个所起的作用都很小，那么这个量就服从或近似服从正态分布。而在经济问题中这些量是很常见的。这就是为什么我们对经济问题进行定量分析时，往往假定在主要因素的影响之外其他各种因素的影响可以用一个服从正态分布的随机变量来描述的原因。

2 极限定理的实际应用

2.1 概率预测

在解决实际问题时，很多总体的分布往往是未知的，或仅知道其分布概型但里面含有未知的参数。这时，我们要了解总体的分布，需要根据以往的统计数据或经验数据来估计未知的参数。因此我们可以采用抽样的方法，利用已知的统计数据或经验数据估计出总体的概率，并将其作为条件，对某事件发生的情况作出预测。

例如：假设人在新冠肺炎传染性疾病流行时的感染率为0.5%，为满足防疫的需要，在某社区随机抽取500 人进行检疫，结果发现感染人数不超过1 人，问该传染病是否已经在该社区流行？

我们不难发现，这类问题经常将样本值与期望值进行比较或将总体的概率与抽样的频率进行比较，这时将很难得到合理的结论，往往需要用概率去预测。

假设该传染病已经在本地区流行，感染率p为0.005，任取500 人进行检疫，则有X人感染的频率为X/500，且X~N(500,0.005)。

由式(1)，可得

2.2 样本容量推断

还有一些问题，我们只知道它可以用二项分布来描述，而总体的概率未知或无法估计，这时根据大数定律，我们可以用抽样的频率来估计总体的概率，但是如何在一定的可信度下，使估计值满足精度的要求？样本容量取多少合适？根据棣莫佛-拉普拉斯中心极限定理，可以给出一种简单的推断方法[6]。

例如：某农场欲购买一大批种子，为了了解某品牌种子的真实发芽率，事先购买了一部分样本进行发芽实验。那么应该先购买多少粒种子，才能使得实验的发芽率与真实发芽率的绝对误差不超过假设推断的可信度

显然总体X（该批种子发芽的数量）服从二项分布，而总体概率p（该批种子发芽的概率）未知，假设先购买了n粒种子X1,X2,…,Xn进行发芽实验，则X1,X2,…,Xn是来自总体X的一个简单随机样本，fn为购买的n粒种子发芽的数量。那么在可信度n应取多少才能使

即满足式(3)的n的值即为所求

可得，对于任意的p，有n2401。

故应先购买2401 粒种子，才能有95%的把握使实验发芽率与真实发芽率的绝对误差不超过0.05。

假如该农场经推断后购买了3000 粒种子做发芽实验，结果有2700 粒种子发芽，此时推断出该批种子的真实发芽率的置信区间(置信水平为95%)是

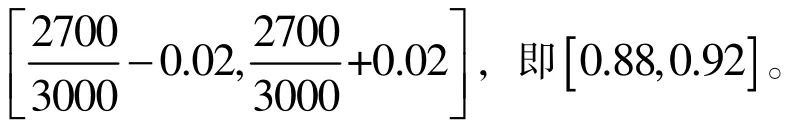
则该农场可根据该置信区间决定是否大批量购买该品牌的种子。

3 结语

中心极限定理在实际生活中的应用非常广泛。本文以中心极限定理为理论依据，针对生活中的一些实际问题，讨论了其在概率预测、样本容量推断等方面的应用，为教学和科研提供一定的参考。