模糊广义决策信息系统的证据特征与信任约简

王志焕, 游小英, 李伟康, 李进金,

(1. 华侨大学 数学科学学院，福建 泉州 362021；2. 闽南师范大学 数学与统计学院，福建 漳州 363000)

模糊集理论[1]是Zadeh教授提出的一种用于刻画目标对象模糊程度的方法.随着模糊集理论的不断发展，其应用范围也越来越广.波兰数学家Pawlak等[2]提出粗糙集理论，它是一种数据处理的数学方法.模糊集和粗糙集理论都是用于研究不确定性的数学工具，将二者结合起来研究具有实际应用价值.目前，已有众多学者对模糊粗糙集的模型及约简问题[3]进行研究.陈应生等[4]通过研究属性重要性度,进而研究不完备信息系统的属性约简.Dubois等[5]通过引入模糊相似关系，最早系统地提出模糊粗糙集理论.Jensen等[6]利用依赖函数，首次设计出一种模糊粗糙集模型的属性约简算法.赵晋欢等[7]构造辨识矩阵对模糊粗糙集进行属性约简，并进行相关实验.陈毅宁等[8]引入基于距离比值尺度的样本集定义，提出基于距离比值尺度的模糊粗糙集，并设计属性约简算法.

证据理论[9-10]提供了一种处理不精确信息的人工智能方法[11]，它能与粗糙集有效结合进行数据处理.根据粗糙集与证据理论的关系，一些学者通过证据理论研究模糊粗糙集的信任结构与属性约简问题，并取得一定的成果.Chen等[12]根据模糊上近似概率与模糊下近似概率探索两种类型的模糊信任和似然函数.Wu等[13]利用广义模糊蕴涵算子[14]，在无限论域中导出广义模糊信任结构.在此基础上，Yao等[15]对模糊决策系统的属性约简问题进行研究.Lu等[16]通过定义一种新的概率测量，研究第2型模糊粗糙集的信任和似然函数.模糊粗糙集理论的决策大多建立在划分的基础上，但以划分刻画决策具有一定的局限性.在现实问题中，多数决策是由覆盖类刻画的，但关于决策为覆盖的模糊粗糙集理论的研究并不多见.基于此，本文对模糊广义决策信息系统的证据特征和信任约简进行研究.

1 预备知识

定义1[1]设集合U为非空论域，当U上的集合X满足由U上一隶属函数X:U→[0,1]表示，则称X为U上的模糊集.其中，X(x)表示x隶属于模糊集X的程度.记U上的模糊集全体为F(U).

假设A,B∈F(U)，定义模糊集的运算为(A∪B)(x)=A(x)∨B(x)=max{A(x),B(x)}；

(A∩B)(x)=A(x)∧B(x)=min{A(x),B(x)}；～A(x)=1-A(x).

定义2[5]设集合U为非空论域，将U×U上的模糊集合R称为U上的一个模糊关系.∀x,y,z∈U，对于U上的模糊关系R，有

1) 若R(x,x)=1，则称R是自反的；

2) 若R(x,y)=R(y,x)，则称R是对称的；

3) 若R(x,z)≥R(x,y)∧R(y,z)，则称R是传递的.

若R满足自反、对称关系，则称R是U上的模糊相似关系；若R满足自反、对称和传递关系，则称R是U上的模糊等价关系.文中讨论的模糊关系是论域U上的模糊相似关系R.

定义3称(U,C,D)为模糊广义决策信息系统.其中，集合U为论域，集合C={C1,C2,…,Cm}为非空有限模糊条件属性集，U上覆盖D={D1,D2,…,Dr}为决策集.

定义4[14]设U为论域，对∀x,y∈[0,1]，定义模糊蕴涵算子I:[0,1]×[0,1]→[0,1]，有

I(x,y)=∧((1-x)∨y).

容易看出，该模糊蕴涵算子满足I(1,0)=0，I(1,1)=I(0,1)=I(0,0)=1.

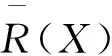
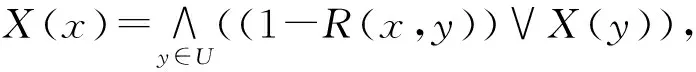
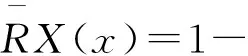
性质1[5]设模糊广义决策信息系统为(U,C,D)，∀X,Y⊆U，∀B,B1,B2⊆C，则有

2)X⊆Y⟹RBX⊆RBY；

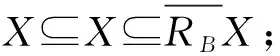
4)B1⊆B2⟹RB1X⊆RB2X.

定义6[5]设(U,C,D)为模糊广义决策信息系统，覆盖D={D1,D2,…,Dr}为决策集，对∀Di∈D,1≤i≤n，Di的下近似与上近似隶属函数分别为

定义7[5]设模糊广义决策信息系统为(U,C,D)，覆盖D={D1,D2,…,Dr}为决策集，1≤i≤r，∀B⊆C，定义模糊正域为

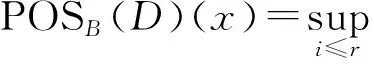
证据理论中的相关概念如下.

定义8[9-10]设U为论域，若集函数m:2U→[0,1]，有

1)m(∅)=0,

则称m为基本概率指派.

根据基本概率指派，可以导出如下信任函数和似然函数.

定义9[9-10]设U为论域，m:2U→[0,1]是基本概率指派，有

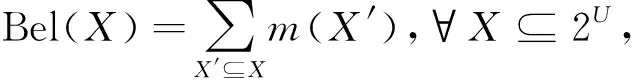
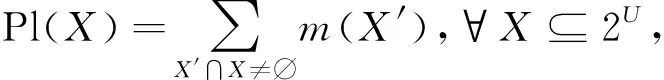
显然，信任函数与似然函数对偶，即Bel(X)=1-Pl(～X).此外，信任函数还满足

1) Bel(∅)=0;

2) Bel(U)=1;

2 模糊广义决策信息系统的证据特征

基于证据理论研究模糊广义决策信息系统的数值特征，即模糊广义决策信息系统的证据特征.首先，定义一个概率测量函数度量模糊集的集合质量.

定义10设模糊广义决策信息系统(U,C,D)，U={x1,x2,…,xn}，对于∀X∈F(U)，Q是论域U上一个概率测量，定义模糊集X的概率为

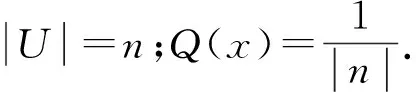
然后，定义一个函数用于构造模糊基本概率指派.

定义11设模糊广义决策信息系统为(U,C,D)，∀X∈F(U)，∀B⊆C，定义函数jB:F(U)→P(U)，即

jB(X)={x∈U|RB(x,y)=X(y),∀y∈U}，

则jB(X)满足

1) ∀X,X′∈F(U)且X≠X′，jB(X)∩jB(X′)=∅；

证明：1) 假设存在x∈U，使x∈jB(X)∩jB(X′)，则RB(x,y)=X(y)=X′(y)，这与X≠X′矛盾.因此，对∀X,X′∈F(U)且X≠X′，有jB(X)∩jB(X′)=∅.

用以上定义的函数构造一个集函数，并证明其符合基本概率指派的两条性质，即证明该集函数为模糊基本概率指派.

定理1设模糊广义决策信息系统为(U,C,D)，∀X∈F(U)，∀B⊆C，定义模糊集函数mB:F(U)→[0,1]，有

则mB为论域U的一个模糊基本概率指派.

综上，mB为U的一个模糊基本概率指派.

对于X∈F(U)，mB(X)表示证据对X的模糊信任度.若mB(X)>0，则称X为mB上的焦元.设Μ为所有焦元的并，称其为核，则称二元序对(Μ，mB)为U上的模糊信任结构.

根据模糊概率指派函数，可直接导出模糊信任函数和模糊似然函数.

经典的信任函数Bel:P(U)→[0,1]，可以把信任函数定义为

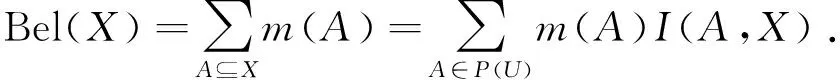
上式中：P(U)为论域U上的全体经典集；I(A,X)为A在X中的包含度，当A⊆X时，I(A,X)=1，否则，I(A,X)=0.

把经典的信任函数推广到模糊的情况下，则对∀X∈F(U)，可以定义模糊集函数Bel:F(U)→[0,1]，即

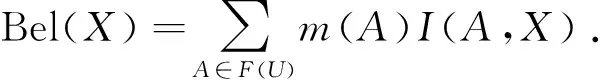
上式中：I(A,X)表示A包含于X中的程度.

定义12设U为论域，对∀A,X∈F(U)，定义蕴涵函数I:[0,1]×[0,1]→[0,1]，有

则模糊信任函数的形式变为

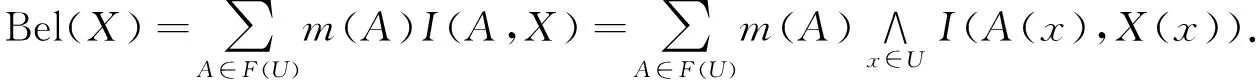
用模糊基本概率指派函数直接导出模糊信任函数和模糊似然函数.

定理2设模糊广义决策信息系统为(U,C,D)，∀X∈F(U)，∀B⊆C，定义模糊集函数BelB:F(U)→[0,1]，即

则BelB为U上的模糊信任函数.

证明：根据定义5、定义10～12及定理1，有

定理3设模糊广义决策信息系统为(U,C,D)，∀X∈F(U)，∀B⊆C，定义模糊集函数PlB:F(U)→[0,1]，有

则PlB为U上的模糊似然函数.

证明：由信任与似然函数对偶的性质，有

由定理2，3可知：模糊广义决策信息系统中的模糊下近似、上近似集合的质量可以用证据理论中的信任函数和似然函数来刻画.

由此，建立模糊广义决策信息系统与证据理论的联系，得出模糊广义决策信息系统基于证据理论的数值特征.下文给出一个实例，用以计算信任函数.

例1考虑评估信用卡申请人的问题.设U={x1,x2,x3,x4,x5}是5个申请人的集合，有4个模糊属性来评估这些申请人：C={C1,C2,C3,C4}.其中，C1表示“教育程度较高”；C2表示“教育程度一般”；C3表示“收入较高”；C4表示“收入一般”.所有申请人在每个模糊属性上的隶属度,如表1所示.

表1 申请人信息Tab.1 Applicant information

若决策为D={D1,D2,D3}，其中，D1表示“待定”；D2表示“申请成功”；D3表示“申请失败”.

对于每个模糊属性Ck，可以定义模糊相似关系，即

同时，定义模糊相似关系R(x,y)=min{RCk(x,y)|Ck∈C},∀x,y∈U.

根据定义的模糊相似关系，可以计算出申请人的模糊关系，如表2所示.假设决策为D1={x1,x4}，

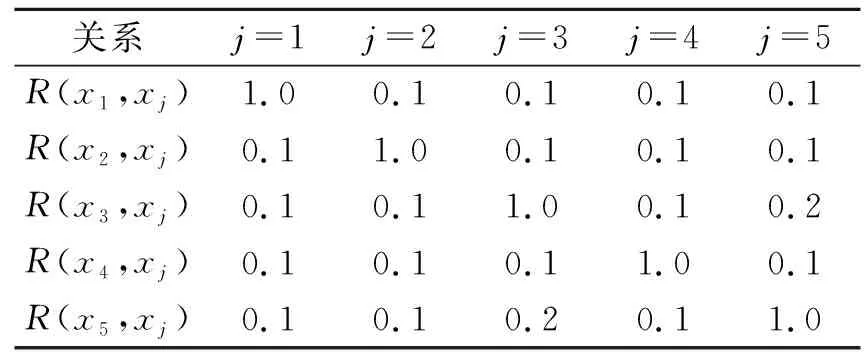
表2 申请人的模糊关系Tab.2 Fuzzy relationship of applicant

D2={x2,x5}，D3={x1,x3,x4}，求解RD1.

根据定义6可知

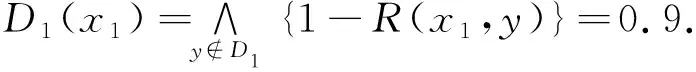
同理可知

RD1(x2)=RD1(x3)=RD1(x5)=0，

RD1(x4)=0.9，

则有

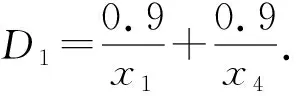
可以计算信任函数，即

同样可计算出

3 模糊广义决策信息系统的信任约简

定义13设模糊广义决策信息系统为(U,C,D)，∀B⊆C，∀x∈U，定义

1) 若LB(x)=LC(x)，∀x∈U，则B是(U,C,D)的模糊下近似协调集.进一步地，若对∀B′⊆B，有LB′(x)≠LC(x)，则称B是(U,C,D)的模糊下近似约简集.

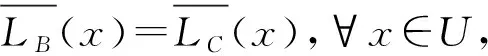
定理4设模糊广义决策信息系统(U,C,D)，∀B⊆C，则

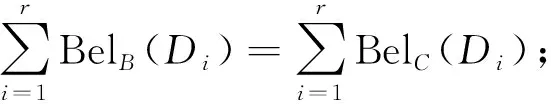
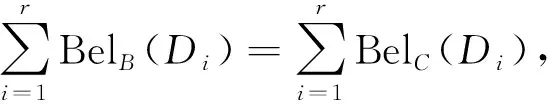
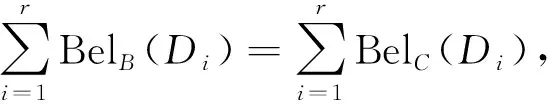
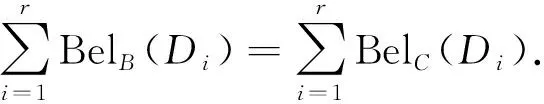
2) 由上文及单调性可证明.

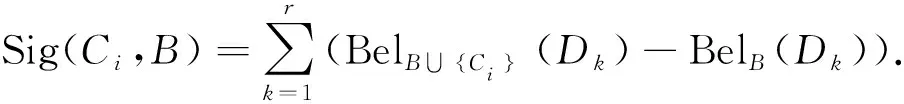
显然，可以得到定理5.

定理5设模糊广义决策信息系统(U,C,D)，若B是模糊下近似协调集，Sig(Ci,C-{Ci})>0，则Ci∈B.

根据定理5可知，关于C的重要度大于0的属性，必属于它的下近似协调集.

由以上定义，可以得出模糊广义决策信息系统的约简算法.

算法1模糊广义决策信息系统的下近似约简算法如下.

输入：模糊广义决策信息系统(U,C,D)；

输出：模糊下近似约简集B.

步骤1令B=∅；

步骤2对于任意的Ci∈C，计算Sig(Ci,C-{Ci})；

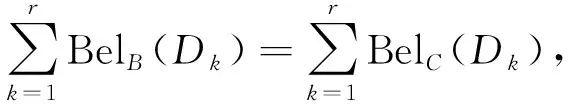
步骤4对于任意的Ci∈C-B，计算Sig(Ci,B)；

步骤5若Ci0∈C-B,满足Sig(Ci0,B)=max{Sig(Ci,B)|Ci∈C-B}，令B=B∪{Ci0}；

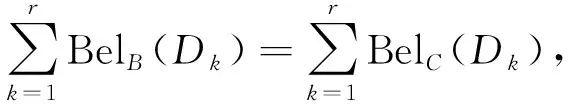
通过一个例子验证算法1.

例2用算法1计算例1的下近似约简.

根据算法1，首先计算

Sig(C3,C-{C3})=0,

Sig(C4,C-{C4})=0.

4 结束语

研究模糊广义决策信息系统的证据特征，利用证据理论对模糊广义决策信息系统中的模糊近似进行数值度量.此外，还利用证据理论中的信任函数给出重要度的定义，提出模糊广义决策信息系统约简的算法，并给实例计算.覆盖类多粒度粗糙集属性约简的仿真实验,以及不同覆盖近似算子约简的联系是亟待解决的问题，也是下一步的研究方向.