部分充填式钢箱砼连续组合梁抗弯承载力分析
2020-10-09郑艳王燕龙
郑艳,王燕龙
(1. 桂林理工大学 广西岩土力学与工程重点实验室,广西 桂林 541004;2. 桂林理工大学 土木与建筑工程学院,广西 桂林 541004)
当前形势下,桥梁结构主要是从大跨度、轻型化和高速化三个方向发展,但是常规的钢混结构已经不能满足桥梁的发展要求.在此背景下,钢混凝土组合结构应运而生,并以其承载能力高、结构自身质量轻、抗震性能相对较好、相比传统钢混结构施工更加方便等一系列突出优点在大跨度桥梁、城市立交桥、高层建筑等工程中得到广泛的应用,取得了显著的经济效益和社会效益.因此,对组合结构深层次的研究必将会成为未来桥梁发展的方向之一[1].钢混凝土组合梁是由钢梁、混凝土翼缘板和剪力连接件构成,可以充分利用钢材抗拉性能好和混凝土抗压强度高的特点[2-3];而部分充填式钢箱砼连续组合梁是在此类组合梁基础上,通过对负弯矩区钢箱下箱室受压区填充混凝土,充填混凝土在钢箱的约束下处于三轴受压状态,从而使其抗压性能得以充分发挥[4-5].混凝土对钢箱壁的约束效应也限制了钢箱向内屈曲,提高了钢箱梁的局部稳定性[6-7].
目前,针对此类组合梁抗弯承载力的计算方法中,主要是围绕两个方面展开:1) 依据弹性理论,按照换算截面法推导钢箱砼连续组合梁弹性极限抗弯承载力;2) 依据塑性理论,求出钢箱砼连续组合梁在塑性极限状态时的抗弯承载力.羊海林等[8-9]根据换算截面原理,并考虑混凝土板参与受拉的程度来确定钢箱砼连续组合梁的截面惯性矩与抗弯刚度,据此得出钢箱砼连续组合梁负弯矩区的弹性抗弯承载力计算公式,根据塑性理论,推出钢箱砼连续组合梁负弯矩区极限抗弯承载力的计算公式.莫时旭等[7]根据弹塑性理论得出钢箱砼连续组合梁极限抗弯承载力计算公式.
由于采用的是柔性连接件,所以交界面处在荷载作用下必然存在相对滑移,而目前对滑移引起的此类组合梁负弯矩区抗弯承载力降低的研究尚不充分.因此,本文借鉴文献[10-12]的思路来研究滑移对此类钢箱砼连续组合梁抗弯承载力的影响.
1 试验概况
1.1 试件设计
本次试验共制作了3片部分充填式钢箱混凝土连续组合梁,编号分别为PFCSCB2-1,PFCSCB2-2和PFCSCB2-3.试验梁具体截面尺寸,如图1所示.梁的上部为120 mm厚的钢筋混凝土板,下部为厚度6 mm的腹板,用4 mm中隔板分成上下两个箱室的钢箱,其顶板和底板厚度10 mm,下箱室填充C40混凝土,混凝土板与钢箱通过圆柱头栓钉连接,试件全长为6 400 mm,跨度为3 000 mm,各项材料的具体参数如表1~3所示.表1~3中:r为抗剪连接度;p为负弯矩区配筋率;fc,Fl为翼板混凝土抗压强度;fc,Fi为充填混凝土抗压强度;E为弹性模量;d为直径(厚度);fr为抗拉强度;fy为屈服强度.

图1 试验梁设计图(单位:mm)Fig.1 Test beam design (unit: mm)
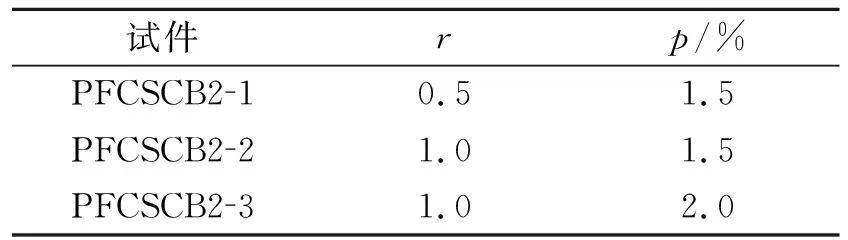
表1 组合梁设计参数Tab.1 Composite beam design parameters

表2 混凝土试验参数Tab.2 Concrete test parameters

表3 钢材试验参数Tab.3 Steel test parameters
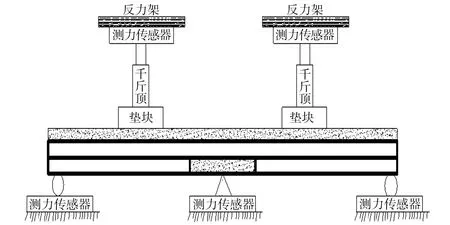
图2 试验加载示意图Fig.2 Schematic diagram of test loading
1.2 加载方案
图2为试验加载示意图.试验采用跨中对称逐级加载的方式,试验测量的内容包括滑移、挠度、应变、滑移和挠度,均通过千分表测量,应变通过应变采集仪测量.
1.3 试验结果
在加载初期,组合梁处于弹性变形阶段,跨中挠度和接触面滑移相对较小;继续加载,中支座负弯矩区混凝土翼缘板表面相继出现多条横向裂缝,并逐渐向两边发展直至裂缝贯通,裂缝宽度超过0.2 mm.同时跨中挠度和交界面相对滑移不断增大,其中,试件PFCSCB2-1因抗剪连接度较小出现栓钉被剪断的现象,并伴有一声巨响.由于负弯矩区混凝土翼缘板开裂逐渐退出工作,受拉钢筋和钢箱的应力增大,变形增加;随后组合梁进入破坏阶段,挠度不断增加,荷载反而降低,试件出现较为明显的弧度,钢筋和钢箱达到屈服应变;跨中加载点处混凝土被压碎且在两个对称加载点处分别出现了一条纵向裂缝并向两边延伸,表明组合梁在到达极限状态时也发生了纵向剪切破坏.
2 连续组合梁负弯矩区弹性抗弯承载力分析
2.1 弹性抗弯承载力受力分析
在弹性阶段,负弯矩区承受较大弯矩,且组合梁负弯矩区在受力过程中,即使是在较小的荷载下混凝土翼缘板也会出现开裂,从而会造成截面刚度的变化.因此,在计算中将其考虑进去.由于钢箱梁和混凝土板是通过柔性连接件连接在一起形成组合结构共同工作,而柔性连接件在荷载作用下会发生变形,造成组合梁交界面发生相对滑移,从而对组合梁的承载力造成一定影响.因此,在计算承载力时也应将其考虑在内.
现有国家标准GB 50017-2017《钢结构设计规范》[13]中对文中所列钢箱砼连续组合梁负弯矩区抗弯承载力的计算方法也没有考虑滑移效应,从而导致其弹性计算结果与实测结果误差偏大,使结构工作状态偏于不安全,不利于钢箱混凝土连续组合梁的推广与应用.
2.2 截面换算

(a) 换算前 (b) 换算后图3 组合梁换算截面Fig.3 Combined beam transformed section
部分填充式钢箱-砼连续组合梁由多种材料组成,因此在计算其截面特征值时,必须根据截面换算原则将由多种材料组成的截面换算为同种材料组成的截面.组合梁换算截面如图3所示.使用等效的钢材代替全部混凝土,并且使截面换算前后的高度保持不变,仅通过改变其宽度,使对应截面换算前后的形心位置不变.根据截面换算的原则,换算后组合梁相应位置的截面面积为
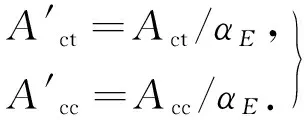
(1)
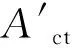
2.3 刚度分析
在分析滑移对负弯矩作用下钢箱砼连续组合梁抗弯承载力的影响时,首先做出以下3点基本假设:
1) 面板混凝土及下箱室填充混凝土不提供拉力;
2) 所用钢筋及钢箱梁皆为线弹性材料;
3) 组合梁交界面的剪力在沿梁长度方向上连续分布.
依据上述假设,交界面的滑移与剪力关系[10-11]满足pv=Ks.其中:p为组合梁纵向栓钉间距;v为组合梁交界面单位长度上的剪力;Ks为栓钉的抗剪刚度.
根据大量栓钉的推出试验,以及本次试验所用栓钉的推出试验统计分析,可得K=0.66NsVu[10-11].其中:Ns为组合梁同一截面上的栓钉数量;Vu为单个栓钉的极限抗剪承载力,根据试验所用栓钉推出试验取值72 kN.
2.4 滑移分析

图4 负弯矩区截面应变分布Fig.4 Sectional strain distribution in negative moment zone
组合梁弹性抗弯承载力极限状态分为以下两种情况讨论:1) 钢箱梁下翼缘首先达到屈服应变;2) 混凝土板中的钢筋首先达到屈服应变.由于在弹性极限状态时混凝土板已经开裂从而退出工作,因此,在计算组合梁弹性抗弯承载力时仅考虑钢箱梁、混凝土板中的纵向钢筋,以及抗剪连接件的作用.
当钢箱梁与混凝土板之间发生滑移时,组合梁负弯矩区截面的弹性应变分布,如图4所示.图4中:εr为钢筋的纵向应变;εbf为钢梁下翼缘的纵向应变;εs为组合梁交界面的相对滑移应变,其求解式[10-11]为
S″(x)=α2S(x)-2βV(x).
(2)
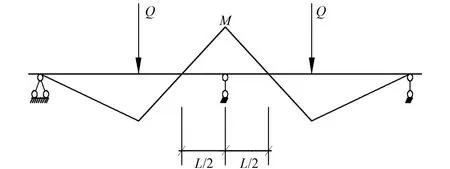
图5 连续组合梁负弯矩区计算模型Fig.5 Calculation model of negative bending moment zone of continuous composite beam
图5为试验计算模型.跨中集中荷载作用下的等跨连续组合梁,设其中支座负弯矩大小为M,则中支座的集中反力p=4M/L,L为组合梁负弯矩区的长度.根据试验梁为对称结构可知中支座处滑移为零,又由反弯点处弯矩为零可知反弯点处组合梁交界面的滑移应变为零.据此,可将边界条件S(0)=0,S′(L/2)=0代入式(2),即可求得跨中集中荷载作用下的滑移[10-11]为
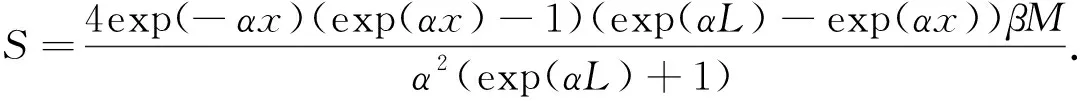
(3)
对上式求导可得滑移应变为

(4)
2.5 滑移影响下的弹性抗弯承载力分析
2.5.1 钢箱梁底板首先屈服 组合梁中支座截面的弹性抗弯承载力为
Meu=Msc+Ty0.
(5)
式(5)中:T为混凝土翼缘板中钢筋所提供的拉力;Msc为钢箱梁横截面所承担的弯矩,其计算为

(6)
式(6)中:f为钢材屈服强度;Wsc为换算截面后钢箱梁与下箱室充填混凝土组合截面的截面抵抗矩.根据节2.2中的相关假定,组合梁中支座截面在达到弹性极限时,其截面应变应满足
f/E+εs+T/(ArE)=Msc/[(EIsc)h0].
(7)
式(7)中:Isc为钢箱与内部充填混凝土组合截面的截面惯性矩;h0为组合梁下翼缘到混凝土翼板中钢筋合力作用点的距离.
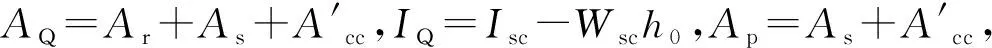
Meu=([ArEεs+AQf]IscWsc-[IscEεs+IQf]ArApy0)/(ApIsc+Arh0Wsc).
(8)
取εs=0即为完全抗剪连接,不考虑滑移时的弹性抗弯承载力为
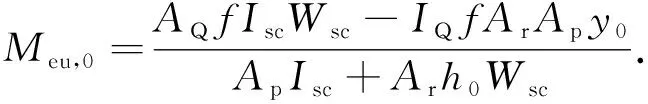
(9)
Meu,0和Meu的差值ΔMeu为考虑滑移效应后组合梁弹性抗弯承载力的下降值,有
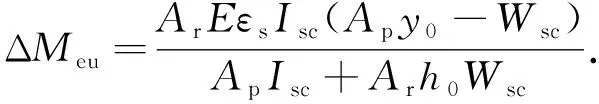
(10)
2.5.2 翼缘板中的纵向钢筋首先屈服 当混凝土翼缘板中的钢筋先于钢箱梁底板屈服时,根据组合截面水平方向力的的平衡关系有
C=T=Arfr.
(11)
式(11)中:fr为钢筋的抗拉强度;C为钢箱(包括内填混凝土)提供的抗力.根据平截面假定并考虑滑移效应后,组合截面应变满足
fr/Er+εs+Msc/(EWsc)+C/(EAsc)=Msc/(EIsc)h0.
(12)
联立式(5),(11),(12),解得
Meu=Arfry0-([ApEεs+AQf]IscWsc)/(ApIQ).
(13)
取εs=0即为完全抗剪连接,不考虑滑移时的弹性抗弯承载力为
Meu,0=Arfry0-(AQfIscWsc)/(ApIQ).
(14)
Meu,0和Meu的差值ΔMeu为滑移效应导致组合梁中支座截面弹性抗弯承载力的下降值,即
ΔMeu=(EIscWscεs)/IQ.
(15)
通过计算发现式(15)为负值,表明当上部钢筋先于钢箱梁底板达到屈服时,组合梁负弯矩区截面的弹性抗弯承载力增大.但是在这种情况下,钢箱梁的下翼缘通常早已屈服.因此,从控制裂缝宽度及安全性的角度出发,认为组合梁在负弯矩作用下的弹性极限抗弯承载力由钢箱梁底板的应力控制,并按照式(8)进行计算.本试验中3个试件在加载过程中皆为钢箱梁底板首先达到屈服也证明了这一观点的正确性.根据式(9)可知,组合截面弹性抗弯承载力的下降程度只与组合截面的特性以及滑移应变的大小有关,与钢筋和钢材的屈服强度无关.
2.6 理论计算值与试验值对比
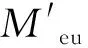

表4 弹性抗弯承载力计算结果与实测结果对比Tab.4 Comparision between calculation results and experimental ones of elastic flexural capacity
由表4可知:试件PFCSCB2-1考虑滑移影响的计算值与实测值相差较大.究其原因,可能是因为部分栓钉在加载过程中发生剪切破坏,试件剪切刚度逐渐降低,从而导致组合梁承载力下降.通过对比试件PFCSCB2-2和PFCSCB2-3可以发现,在相同的抗剪连接度的情况下,提高负弯矩区配筋率,Meu,0和Meu都有所提高.同时还可发现,3个试件中滑移对弹性抗弯承载力的影响均超过10%,因此,在设计时不能忽略滑移对承载力的影响.
3 连续组合梁负弯矩区极限抗弯承载力分析
3.1 极限抗弯承载力受力分析
试验中,组合梁混凝土翼板所配的钢筋截面面积均小于钢箱梁截面面积,因此,组合截面的塑性中和轴不会出现在混凝土翼板中,一般位于钢腹板或接近钢梁箱顶板位置处.由于中支座处在接近极限弯矩时,钢箱梁的上翼缘和下翼缘,以及大部分腹板截面均已大大超过其屈服应变,上部的受拉纵筋也已经屈服,组合梁截面塑性发展比较充分.并且在塑性极限时,钢箱梁上翼缘甚至部分腹板已进入强化阶段.考虑强化效应对组合梁抗弯承载力的有利影响,忽略滑移对抗弯承载力的降低效应,大量试验的实测值与计算值较为吻合也说明了这一点.
参照建筑工程行业标准JGJ 138-2016《组合结构设计规范》[14]中的相关规定,只讨论组合截面塑性中和轴位于钢箱梁腹板时的抗弯极限承载力.根据抗剪连接度的不同分为两种情况:1) 部分抗剪连接;2) 完全抗剪连接.部分充填式钢箱混凝土连续组合梁负弯矩区采用闭口箱形密实截面且下箱室填充了混凝土,负弯矩区没有出现局部屈曲及整体失稳(侧扭屈曲)现象.因此,在计算负弯矩下组合梁极限抗弯承载力时,可按塑性设计方法计算其极限承载力.依据简化塑性理论,可将钢箱梁的应力图简化为等效的矩形应力图,混凝土翼缘板有效宽度范围内的纵向钢筋达到抗拉强度设计值,下箱室充填混凝土均已达到极限抗压强度.
3.2 完全抗剪连接
当采用完全抗剪连接时,组合梁负弯矩区横截面应力,如图6所示.此时,上部翼缘板混凝土开裂退出工作,故不考虑翼缘板混凝土的抗拉作用,但要考虑钢箱下箱室填充混凝土的作用.图6(a)为图6(b)与图6(c)的和,而图6中钢材的应力又可以根据平衡关系分解为图7所示的应力分解图.

(a) 组合梁 (b) 钢材 (c) 充填混凝土 (a) 钢材 (b) 钢箱应力 (c) 钢筋应力 横截面图 应力图 应力图 应力图 平衡图 平衡图图6 塑性中和轴位于钢箱梁腹板内时截面及应力图形 图7 应力图分解及平衡条件 Fig.6 Section and stress pattern with plastic Fig.7 Stress decomposition and neutral axis in web of steel box girder equilibrium conditions
根据平衡条件x=0,有
T′+Arfr=C′+Cw,
(16)
其中:T′=C′.则有
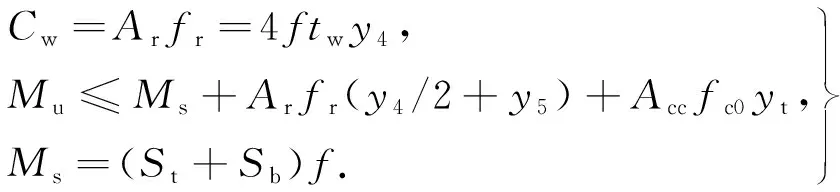
(17)
式(17)中:tw为钢箱单肢腹板宽度(mm);y5为混凝土翼缘板中纵向钢筋合力作用点到组合梁塑性中和轴的距离(mm);y4为组合梁塑性中和轴与钢箱梁塑性中和轴之间的距离(mm);yt为充填混凝土截面形心至组合梁塑性中和轴的距离(mm);St为钢箱梁塑性中和轴以上截面对该轴的面积矩(mm3);Sb为钢箱梁塑性中和轴以下截面对该轴的面积矩(mm3);Acc为填充混凝土面积(mm2);fc0为混凝土极限抗压强度(MPa),根据受压方钢管核心混凝土本构关系取值.
3.3 部分抗剪连接
根据国家标准GB 50017-2017《钢结构设计规范》规定,当计算部分抗剪连接组合梁负弯矩区抗弯承载力时,可按式(16)计算.但Arfs应取nVu和Arfs两者较小值,n取为中支座最大弯矩验算截面至弯矩零点之间的抗剪连接件的数目.

表5 极限抗弯承载力计算结果与实测结果对比Tab.5 Comparision between calculation results andexperimental ones of ultimate flexural capacity
3.4 理论值与实验值对比
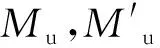
由表5可知:3组试件的计算值与实测值比值在1.02~1.07,两者吻合较好.对比3组试件,还可发现随着配筋率和抗剪连接度的提高,极限承载力也有所提高.
4 结论
综合实验和理论计算,得出以下4点主要结论.
1) 考虑滑移效应影响的两跨连续组合梁弹性抗弯承载力及极限抗弯承载力,其与试验实测结果较为吻合,表明文中所建计算模型与计算方法具有一定的适用性和准确性.
2) 提高负弯矩区配筋率能够一定程度上提高组合梁抗弯承载力,但随着配筋率的提高,对组合梁滑移的影响也逐渐增大.
3) 当抗剪连接度过低时,会导致栓钉被提前剪断,使组合梁交界面产生过大滑移,降低承载力;增大抗剪连接度能够提高组合梁抗弯承载力,但是抗剪连接度过大会导致施工困难.
4) 试验中滑移对组合梁承载力的影响超过10%,因此,在进行组合梁设计时,不能忽略滑移对组合梁弹性抗弯承载力的影响.在选取配筋率和抗剪连接度时,要综合考虑其对承载力及滑移的影响.
