面向特定类的三支概率属性约简算法
2019-09-09彭莉莎钱文彬王映龙
彭莉莎,钱文彬,2,王映龙
1(江西农业大学 计算机与信息工程学院,南昌 330045)2(江西农业大学 软件学院,南昌 330045) E-mail:qianwenbin1027@126.com
1 引 言
与许多经典二支分类模型相比,Yao教授提出的三支决策[1,2]更符合人们在信息不足的情况下解决问题的“三思而后行”的思维方式.三支决策将整体划分成三个部分,从粗粒度到细粒度、从宏观到微观对整体进行分析和处理,通过这种“三划分”思想处理模糊信息数据,可有效提高决策质量,降低错误决策风险,因此,三支决策已成为当前粒计算与知识发现领域中一个重要的研究方向,并在理论模型和应用领域获得广泛研究.理论模型方面包括序贯三支决策[3]、三支聚类[4]、三支区间集[5]和三支模糊集[6,7]等.应用领域包括垃圾邮件过滤[8]、恶意软件分析[9]、人脸识别[10]、和推荐系统[11]等.
在知识发现和粒计算领域中,对高维数据进行属性约简可以提高分类算法的效率和分类性能,且能降低分类过程中的测试代价和误分类代价,因此,属性约简在近些年得到了广泛关注和研究.然而,在经典粗糙集模型的属性约简中,不确定性度量呈现的单调性在三支决策的属性约简中不再成立,于是研究学者们相继提出三支属性约简,这些三支约简方法主要分为三支宏观属性约简和三支微观属性约简.三支宏观属性约简适用于决策类是相互关联的决策系统,即获取所有决策类下的三支属性约简.例如,Chen等人为邻域系统构建基于条件熵的三支决策约简算法[12];Li等人提出邻域决策粗糙集的正域相关和最小代价属性约简[13];Zhang等人在基于依赖度的定性属性约简的基础上提出了基于相对依赖度的三支定量属性约简,并探讨了二者之间的联系与区别[14].Gao等人基于最大包含程度提出最大决策熵,并验证了其单调性,在决策粗糙集模型上构建了基于三支最大决策熵的启发式属性约简算法[15].微观属性约简适用于决策类是相互独立的决策系统,即对单个决策类(简称特定类)进行三支约简,每个特定类的约简子集互不相同.Ma等人从代数论的角度构建了关于经典粗糙集和概率粗糙集的特定类三支属性约简,并分析了二者在一致决策系统和不一致决策系统下的约简结果[16].Zhang等人从代数论和信息论的角度研究了三层粒度结构中的中层结构的Algebra,Likelihood、Prior和Posterior特定类的属性约简算法,并讨论了四种算法下的约简子集的大小关系和基于一致性与不一致性的转换关系[17].
Yao和Zhang详细讨论了三支宏观属性约简与三支微观约简的关系,提到所有决策类的约简子集并不能有效地等同于某个特定类的约简子集,且考虑到约简代价等原因,有时可能只需获取某个特定类的约简子集,这样不仅可以减少约简代价,也能使该特定类的约简子集更精确.例如,在医疗系统中,首先,对初步诊断患有X病的患者进行正域、负域或边界域划分,然后求解这三个域的属性(检测项目)约简结果,就可得知只需检测哪些项目便可判断出这些疑似X类患者一定、不一定或一定不患X病,这在一定程度上可减少检测费用和提高诊断质量.然而,现有针对三支微观约简的研究相对较少,但也逐渐受到关注和探讨[18].为了进一步研究面向特定类的三支属性约简,本文在上述研究基础上,构建了基于相对依赖度和基于信息熵的特定类三支概率属性约简算法,并通过医疗诊断的实例详细分析了算法的有效性和可解释性.
2 基本知识
给定一个决策系统DS=(U,C∪D,{va|a∈C},{Ia|a∈C});其中U={x1,x2,…,xm}表示有限非空对象全集,n-维特征空间C={a1,a2,…,an}表示有限非空条件属性全集,D表示决策属性,va表示a∈C的属性值,Ia|U→va表示一个信息函数,Ia(x)表示对象x在属性a上的值域.关于属性子集B⊆C的等价关系可表示为IND(B)⟺{x,y∈U|∀a∈C[Ia(x)=Ia(y)]},x基于B的等价类[x]B可表示为[x]B={y∈U|xBy}.
2.1 基于概率粗糙集的三支决策
三支决策模型的主要思想是三分而治,即将论域划分成3个域—正域、负域和边界域,并针对这三个域采取有效策略[19].
在三支决策粗糙集中,{λPP,λBP,λNP}和{λPN,λBN,λNN}分别表示当对象x属于对象集X和不属于X时,将x划分到X的正域、边界域和负域的风险损失值.然后,根据期望风险最小化的贝叶斯(Bayes)决策准则计算得出三支决策规则:
定义1[1].给定决策系统DS=(U,C∪D),α和β为损失风险损失值计算而来的三支决策阈值,属性子集B⊆C,∀X⊆U,P(X|[x]B)表示[x]B属于X的条件概率,则对于X构造如下基于概率粗糙集表示的三支决策:
POS(X|B)={x∈U|α≤P(X|[x]B)≤1}
BND(X|B)={x∈U|β NEG(X|B)={x∈U|0≤P(X|[x]B)≤β} 通过三支决策将对象划分到了X的正域POS(X|B)、负域NEG(X|B)和边界域BND(X|B)中. 在启发式属性约简算法中,约简子集应同时满足组合充分条件和独立必要条件,为了便于阐述,在下文中用S和N分别表示这两个条件.S条件用于选择与属性全集具有同等分类能力的属性子集,即约简子集;N条件可去除约简子集中可能存在的少量冗余属性,以确保最终的约简子集尽量最小. 文献[16]提出了关于经典粗糙集模型和关于概率粗糙集模型的特定类三支属性约简方法.关于概率粗糙集模型下的基于代数包含关系的特定类的三支属性约简定义如下: 定义2[16].给定决策系统DS=(U,C∪D)和一对阈值α和β,若R为C关于特定类Dj∈U/D的三支定性约简子集,则其应该满足以下条件: (SPOS):POSα,β(Dj|R)⊇POSα,β(Dj|C) (NPOS):∀(R′⊂R)[POSα,β(Dj|R′)POSα,β(Dj|R)] (SBND):BNDα,β(Dj|R)⊇BNDα,β(Dj|C) (NBND):∀(R′⊂R)[BNDα,β(Dj|R′)BNDα,β(Dj|R)] (SNEG):NEGα,β(Dj|R)⊇NEGα,β(Dj|C) (NNEG):∀(R′⊂R)[NEGα,β(Dj|R′)NEGα,β(Dj|R)] 特定类的核属性可通过依赖度表示为:CORE(Dj)=rα,β(Dj|(C-a)) 同理,属性a∈C-R的重要度可表示为:SIG(a,R)=rα,β(R)-rα,β(R-a). 该文献虽未给出具体的属性约简算法,但详细研究了代数观点下的特定类三支属性约简模型. 文献[17]从信息论的角度,提出了关于经典粗糙集模型的特定类的三种正域属性约简方法(Likelihood、Prior和Posterior),其核心概念如定义3中1)-3)所示. 定义3.[17]给定决策系统DS=(U,C∪D),若R为C关于特定类Dj∈U/D的三支约简子集,则其应该满足以下条件: 1)Likelihood-特定类属性约简-Rlklhd(Dj) (Sklhd):H(Dj|R)=H(Dj|C) (Nklhd):∀(R′⊂R)[H(Dj|R′)>H(Dj|R)] 2)Prior-特定类属性约简-Rprior(Dj) (Sprior):H(R)=H(C) (Nprior):∀(R′⊂R)[H(R′) 3)Posterior-特定类属性约简-Rpstrr(Dj) (Spstrr):H(R|Dj)=H(C|Dj) (Npstrr):∀(R′⊂R)[H(R′|Dj) 其中,令B⊆C,Ci∈U/IND(B),则∀Dj∈U/D,其三支权重熵如下定义: [Hklhd(Dj|P)≥Hklhd(Dj|Q)]∧[Hprior(P)≤Hprior(Q)]∧[Hpstrr(P|Dj)≤Hpstrr(Q|Dj)] 该文献面向经典粗糙集的三支决策模型,从信息论观点研究了特定类的三种正域属性约简算法.而本文则是面向概率粗糙集的三支决策模型,构建基于信息熵的特定类的正域、负域和边界域属性约简算法. 在文献[14]和文献[16]的基础上,从代数观点构建基于相对依赖度的特定类的正域、负域和边界域属性约简算法. 定义4.给定决策系统DS=(U,C∪D)和一对参数α和β,rrelative代表相对依赖度,若R为C关于特定类Dj∈U/D的三支定量约简子集,则其应该满足以下条件: (SPOS):rrelative(Dj|R)≥α (NPOS):∀(R′⊂R)[Rrelative(Dj|R′)<α] (SBND):rrelative(Dj|R)∈(β,α) (NBND):∀(R′⊂R)[rrelative(Dj|R′)∉(β,α)] SNEG:rrelative(Dj|R)≤β (NNG):∀(R′⊂R)[rrelative(Dj|R′) 令*=POS∨BND∨NEG.则在Dj的正域约简、边界域约简和负域约简过程中: ∀a∈(C-R),其属性的重要度为:SIG(a,R)=rrelative(R∪{a})-rrelative(R).将作为启发式属性约简算法中的启发因子. 虽然该方法也是从代数观点下进行属性约简,但2.2小节中提到的是一种基于包含关系的定性属性约简方式,而本小节中构建的是一种基于概率的定量属性约简方式.通过分析可知,当设置(β,α)=(0,1)时,后者可转化成前者.因此,从理论上讲,本小节提出的基于相对依赖度的特定类三支概率属性约简方法的可扩展性相对更强. 为此,以决策系统的相对核CORE为起点,以外部属性的重要性SIG为启发式信息,面向特定类构建基于相对依赖度的三支概率启发式属性约简算法(RRSC-TWDAR),如算法1所示. 算法1.一种面向特定类的基于相对依赖度的三支概率属性约简算法RRSC-TWDAR(下面以“面向特定类下的正域的三支概率属性约简算法”为例) 输入:决策系统DS=(U,C∪D)和参数α和β Step 3.whilerrelative(Dj|R)<αdo Step 4.end while //跳出while循环 ifrrelative(Dj|R-{r})≥αthen R=R-{r}; end if; Step 6.end for //跳出for循环 为了进一步探讨面向特定类的三支属性约简,我们基于概率粗糙集的三支决策模型,给出了基于信息熵的特定类的正域、边界域和负域的属性约简模型和算法. 定义5.给定决策系统DS={U,C∪D}和一对阈值α和β,特定类Dj∈U/D,属性子集B⊆C,P(Dj|[x]B)表示等价类[x]B属于Dj的条件概率,则关于特定类Dj构造如下基于概率粗糙集表示的三支决策: POS(Dj|B)={x∈U|α≤P(Dj|[x]B)≤1} BND(Dj|B)={x∈U|β NEG(Dj|B)={x∈U|0≤P(Dj|[x]B)≤β} 令*=POS∨BND∨NEG.则关于特定类Dj基于信息熵的正域、边界域和负域的约简中: 算法2.一种面向特定类的基于信息熵的三支概率属性约简算法(ITSC-TWDAR) 输入:决策系统DS=(U,C∪D) R=R∪{a0}; Step 4.end while R=R-{r}; end if; Step 6.end for 算法2与算法1相比,除了启发因子不一样,整体设计思路也是以核属性为约简子集的起点,依据S条件,依次添加最重要的属性至约简子集中,直至达到与属性全集具有相同的划分能力后跳出循环,最后,依据N条件,剔除粗糙约简子集中的冗余属性,直至最终获取到一个尽量最优的约简结果. 算法2的最佳运行时间有两种: 算法1和算法2基于概率三支决策模型,简述了基于相对依赖度和信息熵的特定类的三支属性约简过程,为了进一步说明这两种算法的有效性和可解释性,下面以表1为例进行分析和说明,并详细给出算法1和算法2对一致决策系统和不一致决策系统的计算过程. 某医院诊断系统,如表1所示,xI代表病人,aI代表病症,D为诊断结果.算法的有效性为:根据初步诊断结果分为三类病人,将患有“Φ”病的一类病人D1={x1,x2,x3}作为特定类,对其进行三支概率属性约简.算法的可解释性为:D1的约简子集即为医生诊断病人是否患“Φ”病时需要检查的部分病症.即:检查RPOS(D1)可知,POS(D1)中的病人患有“Φ”病、检查RBND(D1)可知BND(D1)的病人可能患有“Φ”病;检查RNEG(D1)可知NEG(D1)中的病人不患“Φ”病. 表1 某医院诊断系统 一致表不一致表Ua1a2a3DUa1a2a3Dx1010Φx1100Φx2010Φx2011Φx3011Φx3001Φx4001Ψx4011Ψx5001Ψx5001Ψx6101Ψx6021Ψx7100Ωx7010Ψx8100Ω/////x9110Ω///// 设置阈值α=0.8;β=0.2,根据定义1可知,基于概率粗糙集的三支决策计算D1的正域、负域和边界域,计算结果如表2,表中D1中的对象用粗体表示. 根据算法1和算法2,在实际应用或对大数据进行降维处理时,无需计算每个属性子集下的相对依赖度和信息熵,但为了更详细直观地根据相对依赖度和信息熵来分析两个算法的计算步骤,我们将所有计算结果置于表3中. 表2D1在各属性子集下的正域、负域和边界域 属性子集 一致表不一致表BPOS(D1)BND(D1)NEG(D1)POS(D1)BND(D1)NEG(D1){a1,a2,a3}{x1,x2},{x3}ø{x4,x5},{x6},{x7,x8},{x9){x1}{x2,x4},{x3,x5}{x6},{x7}{a2,a3}{x3}{x1,x2,x9}{x4,x5,x6},{x7,x8}{x1}{x2,x4},{x3,x5}{x6},{x7}{a1,a3}{x1,x2}{x3,x4,x5}{〛x6},{x7,x8,x9}{x1}{x2,x3,x4,x5,x6}{x7}{a1,a2}{x1,x2,x3}ø{x4,x5},{x6,x7,x8},{x9}{x1}{x2,x4,x7},{x3,x5}{x6}{a1}ø{x1,x2,x3,x4,x5}{x6,x7,x8,x9}{x1}{x2,x3,x4,x5,x6,x7}ø{a2}ø{x1,x2,x3,x9}{x4,x5,x6,x7,x8}ø{x1,x3,x5},{x2,x4,x7}{x6}{a3}ø{x1,x2,x7,x8,x9}{x3,x4,x5,x6}ø{x1,x7},{x2,x3,x4,x5,x6}ø 下面将根据算法1和算法2,以表1左侧中的一致表为例,详细计算代数观点和信息论观点下的特定类D1的正域、边界域和负域约简过程和结果,以下算法中的步骤与第3节中算法1和算法2一一对应.. 算法1. 1.正域约简: 第1步.计算特定类D1的正域约简中的核属性. rrelative(D1|C-{a1})=0.333<α=0.8; rrelative(D1|C-{a2})=0.667<α=0.8; rrelative(D1|C-{a3})=1>α=0.8; 第2步.将第1步计算而来的核属性赋值给R,并将R作为正域约简的起点. 第3步.不断添加重要的属性到R中,直至获取到与属性全集具有相同划分划分能力的约简子集. 第4步.因为Rrelative(D1|R)=Rrelative(D1|{a1,a2})=1>α所以跳出while循环,此时R={a1,a2}. 第5、6步.剔除R中的冗余属性. 第8步.输出D1的最终的正域约简子集: 上述属性约简结果的语义解释:医生只需要检查{a1,a2}两项病症便可诊断出{a1,a2}下的POS(D1)中的{x1,x2,x3}患有Φ病,既能减少检查费,又能减少病人的检查时间和检查疼痛等代价. 表3 各属性子集关于D1的相对依赖度和信息熵 属性子集 一致表不一致表BrrelativeHPOSITHBNDITHNEGITrrelativeHPOSITHBNDITHNEGIT{a1,a2,a3}1.0000.2510.0000.5021.0000.1210.1570.212{a2,a3}0.3330.1060.1590.3041.0000.1210.1570.212{a1,a3}0.6670.1450.1590.2651.0000.1210.1420.106{a1,a2}1.0000.1590.0000.4101.0000.1210.3040.106{a1}0.0000.0000.1420.1571.0000.1210.1420.000{a2}0.0000.0000.1570.1420.0000.0000.3180.106{a3}0.0000.0000.1420.1570.0000.0000.2870.000 2.边界域约简: 第1步.计算特定类D1的边界域约简中的核属性. rrelative(D1|C-{a1})=0.333∈(β,α); rrelative(D1|C-{a2})=0.667∈(β,α); rrelative(D1|C-{a3})=1∉(β,α); 第2步.将核属性赋值给R,作为边界域约简的起点. 第3步.获取D1初步的边界域约简子集. 因为rrelative(D1|R)=rrelative(D1|{a3})=0∉(β,α),且SIG(a1,R,D1)=0.667>SIG(a2,R,D1)=0.333,所以选出C中除a3外最重要的属性(a0=a1)并入R中,即R=a3∪a1={a1,a3},此时rrelative(D1|{a1,a3})=0.6667∈(β,α), 第4步.结束while循环. 第5步.剔除冗余属性. rrelative(D1|{a1,a3}-{a1})=rrelative(D1|{a1,a3}-{a3})=0∉(β,α). 第6步.结束for循环. 第8步.输出D1的最终的边界域约简子集. 上述属性约简结果的语义解释:如果医生检查{a1,a3},便可诊断出{a1,a3}下的BND(D1)中的x3、x4和x5可能患有Φ病.假设检查a2的费用远高于检查a3的费用,若病人x3经济条件受限又想知道自己是否可能患有Φ病的时候,则可选择这种诊断方案. 3.负域约简: 第1步.计算特定类D1的负域约简中的核属性. rrelative(D1|C-{a1})=0.3333>β=0.2; rrelative(D1|C-{a2})=0.6667>β=0.2; rrelative(D1|C-{a3})=1>β=0.2; 因为负域约简算法不同于正域约简算法1,此时省略第3步和第4步. 第5步.依次剔除最重要的属性,直至rrelative(D1|R)<β. 此时rrelative(D1|R)=rrelative(D1|C)>β∧|R|>1,进入while循环,依次剔除最重要的属性,因为SIG(a1,R,D1)=0.667>SIG(a2,R,D1)=0.333>SIG(a3,R,D1)=0,所以a0={a1},即R=C-a1={a2,a3},此时,rrelative(D1|{a2,a3})=0.333>β,因此继续剔除重要属性,因为SIG(a2,R,D1)=SIG(a3,R,D1)=0,按顺序选择a0={a2},即R={a2,a3}-{a2}={a3},此时rrelative(D1|{a3})=0<β. 第6步.跳出for循环. 上述属性约简结果的语义解释:如果医生只检查a3,便可诊断出基于a3划分的NEG(D1)中的{x3,x4,x5,x6}不患Φ病. 同理,可基于相对依赖度获取不一致表中D1的三支概率约简子集,计算结果如表4所示. 算法2. 1.正域约简: 第1步.基于信息熵计算D1的正域约简的核属性. 第2步.将核属性赋值给R. 第3步.获取与C具有相同的正域划分能力的属性子集R. 上述属性约简结果的语义解释:通过基于信息熵的属性约简方式进行医疗诊断,医生必须同时检查{a1,a2,a3}这三种病症,才能确诊POS(D1)中的{x1,x2,x3}都患Φ病.对比分析可知,通过相对依赖度的属性约简方式进行医疗诊断时,医生只检查{a1,a2}也能{x1,x2,x3}都患Φ病.虽然后者比前者的诊断成本更高,但诊断结果没前者精准. 2.边界域约简: 第1步.计算D1的边界域约简的核属性. 第3步.依次选取最重要的属性存入R中,直至R划分边界域的信息熵高于C划分边界域的信息熵. 上述属性约简结果的语义解释:医生通过检查a3可诊断出BND(D1)中的{x1,x2,x7,x8,x9}可能患Φ病. 3.负域约简: 第1步.计算D1的负域约简的核属性. 第3步.获取与C具有相同的负域划分能力的属性子集R. 上述属性约简结果的语义解释:医生必须检查{a1,a2,a3}这三个项目,才能确诊NEG(D1)的{x4,…,x9}不患Φ病,同时也能推断出{x1,x2,x3}一定或可能患Φ病. 同理,基于信息熵计算不一致表中D1的三支概率约简子集,计算结果如表4所示. 表4 特定类三支概率属性约简结果 各域约简子集一致表不一致表RPOS(D1)RPOSrelative(D1){a1,a2}{a1}RPOSIT(D1){a1,a2,a3}{a1}RBND(D1)RBNDrelative(D1){a1,a3}NULLRBNDIT(D1){a3}{a2}RNEG(D1)RNEGrelative(D1){a3}{a2}RNEGIT(D1){a1,a2,a3}{a2,a3} 通过表4中的基于相对依赖度和基于信息熵的特定类的三支概率属性约简结果可知:不一致表下的约简子集要小于一致表下的约简子集;基于相对依赖度求解的约简子集要小于基于信息熵求解的约简子集,但前者有时可能较难获取不一致表的边界域约简,且其约简子集下的分类准确率一定程度上低于后者.综上分析,两种算法都有各自的优缺点,因此,在实际应用中,应根据决策系统的数据特征、可承受的约简代价范围和所期待的分类准确率等实际情况选择最合理的约简方式. 本文提出了代数观点下的基于相对依赖度和信息论观点下的基于信息熵的三支概率属性约简方法,并对不同决策系统中的特定类的正域、边界域和负域的进行了有效地属性约简,为人们在现实生活选择不同的决策方式提供了依据,也一定程度上减少了人们的决策代价. 针对决策系统中的特定类,本文从代数和信息论视角,分别构建了基于相对依赖度和基于信息熵的正域、负域和边界域约简模型,并给出了对应的启发式的属性约简算法.通过医疗诊断的实例详细分析了两种算法在一致决策系统和不一致决策系统上的约简过程,并给出了有效的约简结果,进一步验证了算法的可行性和可解释性.在下一步研究计划中,将研究基于信息论中的条件熵和其他熵对特定类的三支概率属性约简方法,并通过实验分析算法的约简效率和分类精度,同时对比已有的相关算法.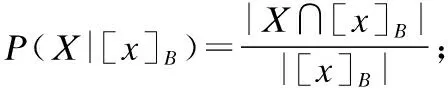
2.2 基于代数观点的特定类的三支属性约简
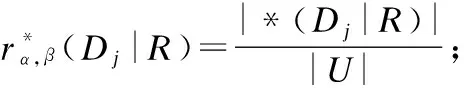
2.3 基于信息论的特定类属性约简

3 面向特定类的三支概率属性约简
3.1 代数观点下的特定类三支概率属性约简
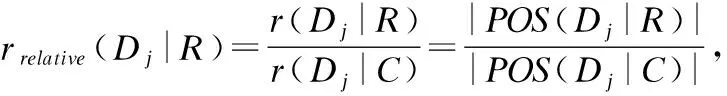

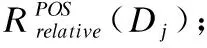

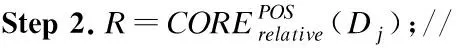

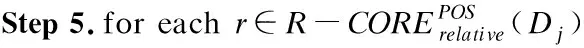
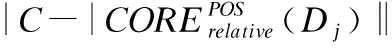
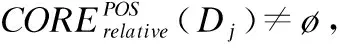

3.2 基于信息论的特定类三支概率属性约简
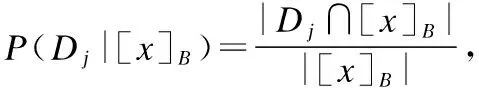

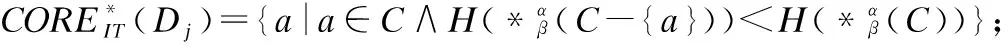


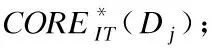





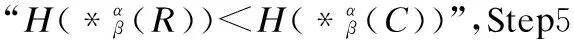
4 实例分析
Table 1 A hospital diagnostic system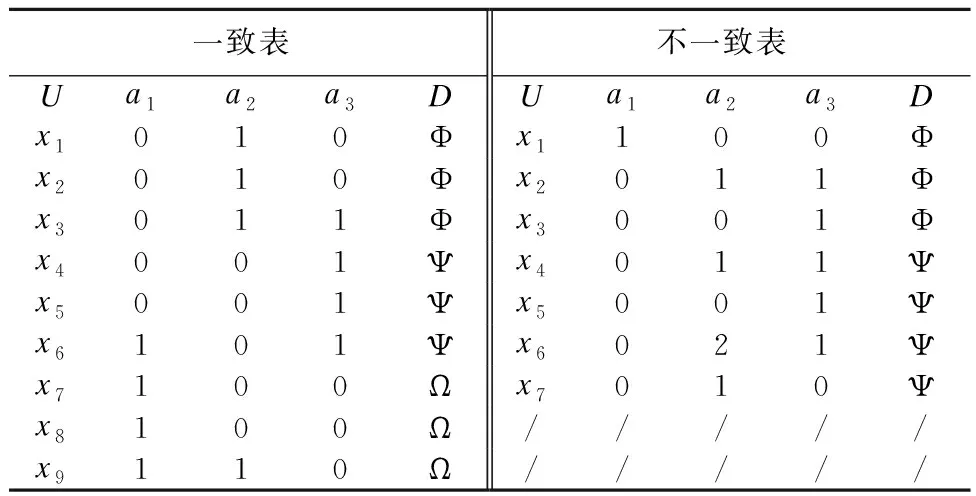
Table 2 Positive,negative,and boundary regions ofD1under each attribute subset
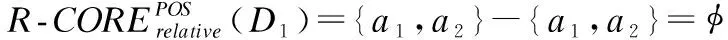

Table 3 Relative dependence and information entropy ofD1under each attribute subset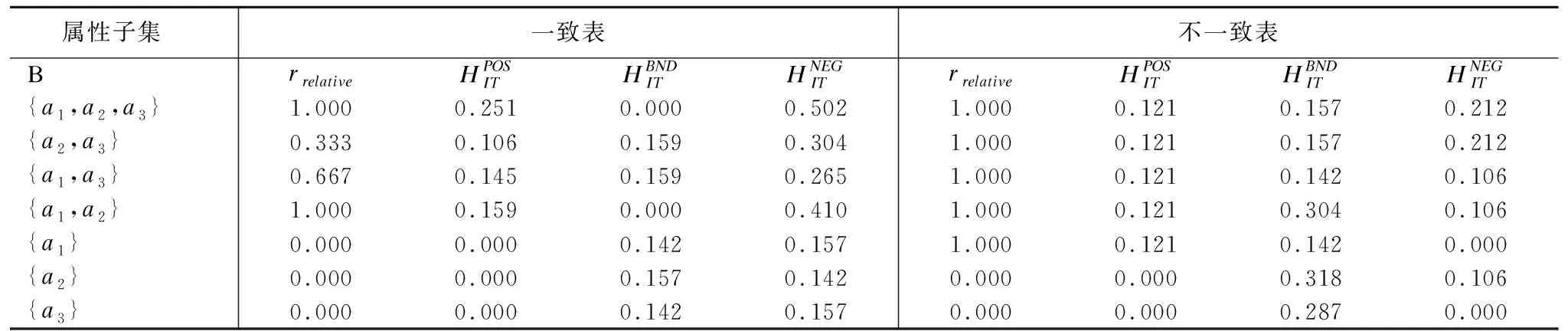
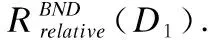
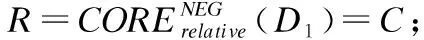
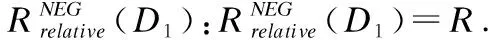
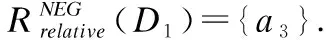

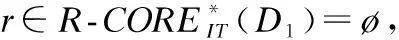





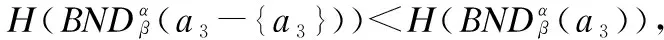
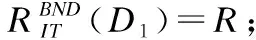
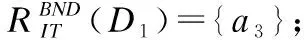

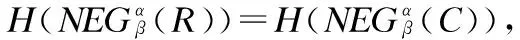
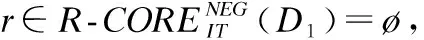
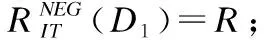
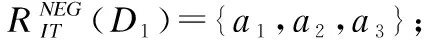
Table 4 Three-way probabilistic attribute reduction results on class-specific
5 总 结
