基于中美教材比较谈表内除法

陆晓峰

(合肥市卫岗小学 安徽合肥 230051)

为了研究方便，本文中作为样本的中国教材，选用的是江苏教育出版社出版的义务教育教科书《数学》(以下简称苏教版教材)。而作为样本的美国教材，则选用美国霍顿米夫林哈考特出版社出版的Go Math教材(以下简称Go Math教材)。

除法求商是中美小学数学教材中都有的内容，中国教材(内地)以乘法口诀表为基础，将使用乘法口诀求商的除法称为“表内除法”，而美版教材没有乘法口诀，求商方法较为多样，利用乘法表(10×10)求商只是其中一种。

作为没有乘法口诀的数学体系，了解美国教材如何求商，“他山之石，可以攻玉”，可以加深我们对除法求商本质的理解，为教学寻求更灵活的方法和策略。

一、中美教材各是如何编排有关0～10各数的除法内容

(一)教学年级

苏教版教材表内除法安排在二年级上册，Go Math安排在三年级。

(二)编排顺序

苏教版教材“表内除法”分两段教学，第一段：第四单元“表内除法(一)”，先“认识除法”，再学习“用1～6的乘法口诀”求商；第二段：第六单元“表内乘法和表内除法(二)”，“7～9的乘法口诀”和“用7～9的乘法口诀求商”的学习同步进行。

Go Math教材把这部分内容安排在三年级第6、7单元，其中第六单元主要内容为“理解除法”，第七单元主要内容是“除法策略”。

苏教版教材“认识除法”这部分内容有6个例题，例1讲“平均分”，例2讲“包含除”，例3是“等分除”，例4是两种分法对比，例5开始除法的初步认识，例6认识除法算式各部分名称。

把两版教材进行简单对比，发现其中有部分内容可以相互对应。苏教版教材中“平均分”的内容对应Go Math 教材中“除法模型”，而苏教版教材的“包含除”其实就是Go Math教材中寻找“组”的数量，而“等分除”就是“组”的大小，也就是每“组”几个。除法引入及除法各部分的名称，Go Math教材放在例4 Bar Models(条形模型)内介绍。除此之外，两版教材中都各有部分内容互不对应。比如两种分法的整理，苏教版教材有，而Go Math教材没有；再比如，Go Math在这个单元中安排的五种求商方法以及关于1和0的除法规则则是苏教版教材中所没有的内容。

苏教版教材Go Math教材单元名称表内除法(一)理解除法例题内容例1:平均分例2:包含除例3:等分除例4:两种分法整理例5:除法的初步认识例6:除法算式各部分名称例1:问题解决:除法模型例2:组的大小(每组数量)例3:组的数量例4:条形模型例5:联系减法和除法例6:阵列模型例7:联系乘法和除法例8:写关联算式例9:关于1和0的除法规则

根据Go Math第7单元的内容和概述做简单对比，苏教版表内除法的编排顺序是除以1～6作为一个整体，与乘法口诀的编排顺序一致，然后依次是除以7、8、9，也和乘法口诀学习保持同步。Go Math则有着特殊的编排顺序：除以2，10，5，3，4，6，7，8，9，表面上看似乎毫无规律可言，那么这样的编排顺序依据是什么，你能想到吗？

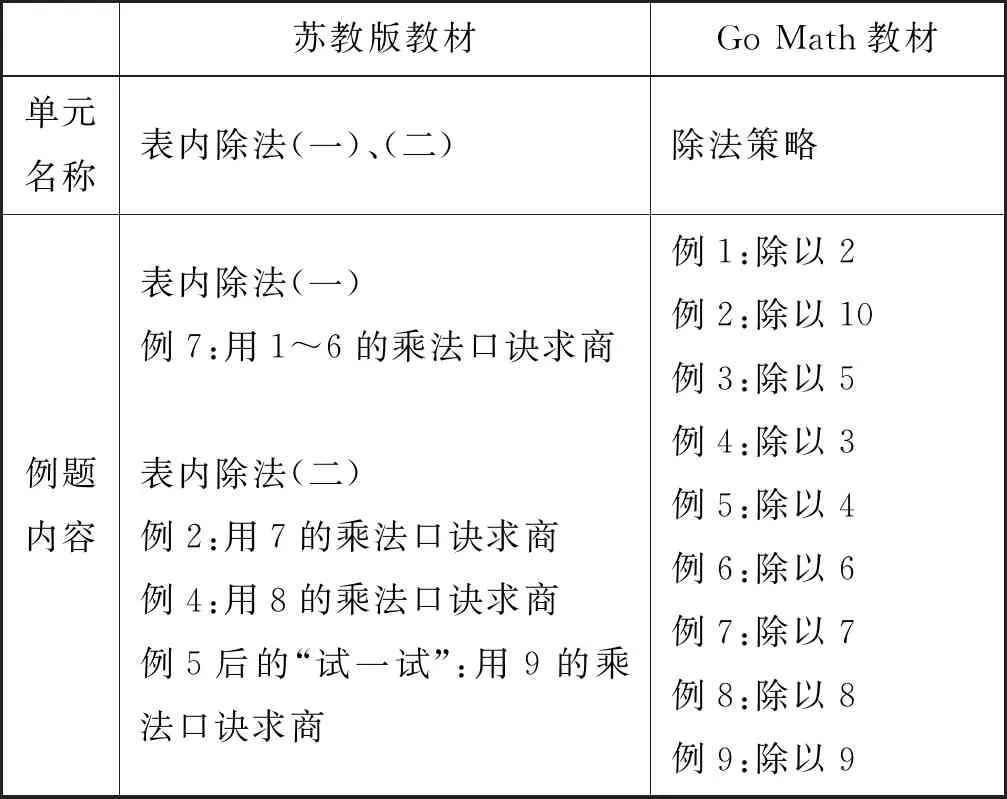
苏教版教材Go Math教材单元名称表内除法(一)、(二)除法策略例题内容表内除法(一)例7:用1～6的乘法口诀求商表内除法(二)例2:用7的乘法口诀求商例4:用8的乘法口诀求商例5后的“试一试”:用9的乘法口诀求商例1:除以2例2:除以10例3:除以5例4:除以3例5:除以4例6:除以6例7:除以7例8:除以8例9:除以9

二、中美教材除法求商各有哪些方法

苏教版的求商方法在介绍口诀求商之前有两种：“圈一圈”“分一分”，分别对应“包含除”和“等分除”两种情况。

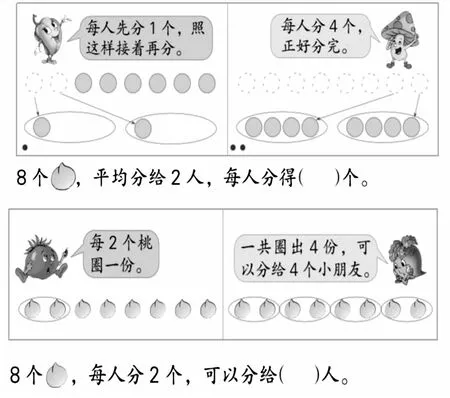
而Go Math的求商方法五花八门，先说在第6单元出现的6种：

第一种：直观操作，用筹码或在集合圈内圈一圈，和苏教版教材中的“圈一圈” “分一分”类似。

第二种：联系减法，以12÷2求商为例，12连续减2，减6次之后为0，则商为6。

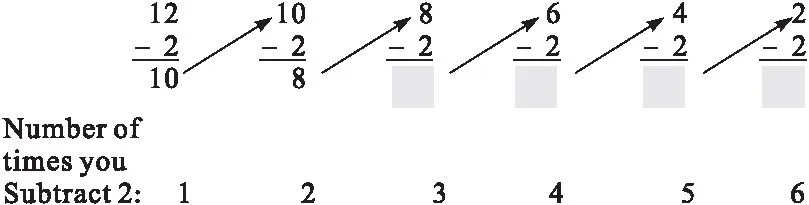
第三种：联系乘法，这种和用口诀求商类似，只是这里是利用乘法算式求商。

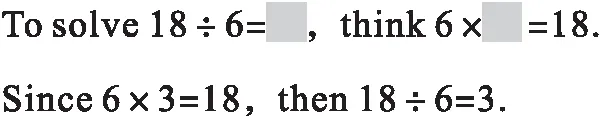
第四种：利用一组有关联的算式求商。

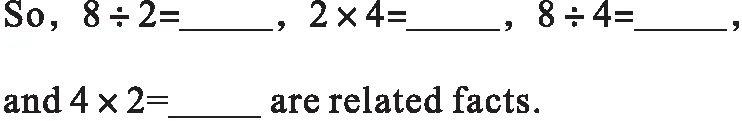
第五种：Bar Models(条形模型)，利用几何直观，用长条代替数字思考。

第六种：阵列模型，利用方块进行直观操作，形成行列数分别为两个因数的阵列来寻找答案。

接下来，正式教学除法求商的阶段。苏教版教材教学用口诀求商的例题以“除以2”开始，而Go Math教材也有这个内容，接下来我们就以“除以2”为例，具体看一看两版教材是如何分别教学求商方法的。

苏教版教材在例题中预设了四种方法：1.直观操作；2.联系减法；3.联系乘法意义；4.口诀求商。查阅教参，有如下说明：学生如果没有出现联系减法来求商，可以不用介绍。实际教学时，教师也将大量时间花在“用乘法口诀求商”这种方法上，从例题的重点指导到课后练习的设计，力求每位学生都能掌握“用乘法口诀求商”这种方法，至于例题中出现的另三种方法，在课后练习中未出现。

Go Math教材“除以2”预设了两种方法，都是直观操作活动，教材这一页的标题也很醒目：“除以2(或者被2除)”，教材本页还呈现了本课的基本问题：“除以2”的含义是什么？接着呈现本课的学习目标：你将学习用筹码来构建“除以2”的模型并且写出除法算式。

Go Math教材中的例题被称为“解锁真实世界的问题”， 活动1的问题是：玛丽莎的后院有10只蜂鸟，2个饲养员，如果每个饲养员养的蜂鸟只数相等，那么他们每个人养几只？右边呈现提示性的问题或操作指南：

“你需要找出什么？”

“圈出你需要用到的数字。”

“你准备用什么工具来帮助解决问题？”

学生将依据这样的思考和操作步骤，聚焦问题，解决问题。

活动2的问题与之相反，是平均分的另一种分法，同样地能通过提示性问题和操作指南帮助学生解决问题。

因为没有乘法口诀，我们可以发现，Go Math教材“除以2”只教了直观操作的方法，而同时，因为有乘法口诀，苏教版教材开始聚焦这种方法，并在课后练习中大量使用。

之前我们说过Go Math教材第7单元“除法策略”的编排顺序有些特别，苏教版教材“除以2”之后，就是教学“除以3”，因为乘法口诀的编排顺序就是按9以内数字大小顺序编写，而Go Math教材在“除以2”之后，安排的是“除以10”，学习用乘法表求商，Go Math教材的乘法表是10×10的表格。以50÷10为例，明确告知学生：“因为除法是乘法的逆运算，所以你可以用乘法表来求商。”教学生先在顶栏找到因数10，然后向下找到乘积50，再向左找到未知因数5，商就是5。之后教学“除以5”，因为“除以5”可以用“除以10”的商倍加，举例来说，就是20÷10是2，那么20÷5就是2加2，商是4。“除以4”，可以是先“除以2”，再“除以2”，“除以6”相当于先“除以2”，再“除以3”，因为除以一个数等于分别除以这个数的因数。还有求商也可以用加法算，商是除数累加到被除数的次数等等，基于这样的分析，我们可以认为这样的编排顺序是为了要结合数字特点教学不同的除法求商策略而有意为之的。

从委员会的架构可以看出，赫尔辛基委员会的组织架构非常成熟，委员会自上而下内部分工科学、明晰，与外部的整合、拓展和跨界合作也已经得到很好的机制化。波罗的海海洋环保合作重视决策科学性的特色、多元主体的参与的特色、跨界合作的特色等都通过制度化设计的方式得以固定下来。赫尔辛基委员会的良好运行，使得公约和波罗的海行动项目的各项规定和措施得以有效的落实。同时，委员会在海洋环保合作实践过程中不断积累经验、发现问题、积极调整和整合新的政策领域，使得委员会成为一个组织完整性、包容性程度很高的不断成熟的组织。

三、中美教材编排的侧重点是否一样

通过对两版教材的梳理，苏教版在教学完用1-6的乘法口诀求商之后，通过大量的算式和解决问题练习来帮助学生熟练掌握用口诀求商的方法，力求的是“又对又快”。而Go Math教材会根据数字特点教学不同的求商策略。我们很容易想到：苏教版教材更侧重正确并熟练计算，而Go Math教材更加关注策略，教会学生利用四则运算之间的关系、各种模型及运算规律来解决问题。

教科书的编写体现的是课程标准的“意志”，两国教材编排的侧重点如此不同，在课程标准中可以寻找到源头。我国课程标准中有关“表内除法”的要求是：

1.结合具体情境，体会整数四则运算的意义。

2.能熟练地口算表内乘除法。

而CCSSM将这部分内容归类为“运算和代数思维”领域，具体要求为：

表征和解决有关乘除法的问题；理解乘法的性质以及乘除法之间的关系；100以内的乘除法；解决含有四则运算的问题，认识和解释其中的算术规律。

四、美国Go Math版教材有哪些值得学习和借鉴的地方

(一)教材设计更符合认知规律

Go Math教材既有呈现全册各单元内容的总目录，每个单元也会有各自的目录，目录页中会有本单元的基本概念的解释、本知识体系的概念图以及本单元力求解决的问题等。以第6单元为例，单元目录中介绍了本单元要研究的问题：怎样用除法来找到“组”的大小或 “组”的数量？乘除法有怎样的联系？什么模型能帮助做除法？怎样利用减法来做除法？反观国内的几版教材，基本上只有全书目录页且只呈现各单元名称，没有单元目录页，学生也无法从教材中清晰地感知到每节课的数学问题和学习目标，教材的练习功能大于指导功能。

(二)早期代数思维的引入尝试

(三)对教学的启示

首先，我们要有文化自信，乘法口诀是祖先的智慧，从几个相同加数的和开始，到用乘法算式表示，再到用口诀帮助记忆算式及结果，口诀是求几个相同加数和的记忆载体，用口诀求商使中国学龄儿童在表内除法计算中拥有一定的优势。

但是，作为数学教师，我们更要明白，乘法口诀是求商的一种策略，但不是全部策略，结合直观操作、减法模型、分解因数等也可以求商，而且这些策略既可以帮助学生更好地理解四则运算的含义及相互关系，更可以适应更复杂的情境及开放性问题。