移动荷载作用下考虑纵向连接间隙的浮桥结构计算

2020-09-28黄恒陈徐均施杰魏枭

兵工学报 2020年8期

黄恒，陈徐均，施杰，魏枭

(陆军工程大学野战工程学院，江苏南京 210007)

0 引言

浮桥是克服江河障碍的一种重要水上通道，其架设速度快，建造成本低，受河流的水深、河幅、河底土壤环境影响较小，在军事和民用中都发挥着重要作用[1-4]。目前已建成浮桥的结构形式主要包括连续钢筋混凝土浮箱结构、浮箱支撑的桁架上铺设桥面板结构(桥脚分置式结构)、桥脚舟与桥跨结构合为一体的带式浮桥结构等[5-7]。本文涉及的计算方法主要适用于带式浮桥。

车辆在浮桥上行驶的速度对浮桥吃水以及浮桥内力会产生较大影响，通常速度增大，浮桥吃水增大，其结构受力也会发生变化。定量分析车辆移动速度对浮桥的影响，对于浮桥的正常使用至关重要。另一方面，为了便于浮桥架设拼组以及优化结构受力，浮桥的纵向连接处通常存在连接间隙，图1即为带式浮桥纵向连接处实图[8]。连接间隙在荷载作用下会闭合，对浮桥的整体变形和受力产生影响，在浮桥的静态和动态分析中必须加以考虑。连接间隙的合理取值，对于优化浮桥结构十分重要。

图1 浮桥纵向连接处Fig.1 Longitudinal connection of floating bridge

对于浮桥结构的计算分析，已有多位学者进行了相关研究。Wu等[9]将静水作用力简化为线性弹簧和阻尼器，分析并得到了移动荷载作用下刚性浮体的运动特征。Giske等[10]基于1阶和2阶可靠性反求方法，给出了大跨度浮桥在波浪荷载作用下长期极限响应分析方法。林铸明等[11]推导了移动荷载作用下弹性基础梁的计算方法。陈徐均等[12]对通载浮桥动态位移的测试方法与数据分析进行了研究。Zhang等[13]基于简支梁理论，建立带式浮桥在移动荷载作用下的数学模型，分别对恒力荷载和质量荷载作用下的浮桥动力特性进行了模拟计算。孙建群等[14]通过水动力模型试验，计算了多模块浮桥在规则波作用下的水动力响应和弯矩分布情况。付世晓等[15-17]研究了间隙对拼组式浮桥静态响应的影响，以非线性有限单元法为基础，用Newmark直接积分和Newton-Raphson迭代方法求解，研究了移动荷载作用下非线性连接浮桥的三维非线性动力响应特征；此外，他们还通过模型试验测量了动荷载作用下的浮桥竖向位移，得到了由多个非线性连接模块组成的带式浮桥在移动荷载作用下的水弹性响应。江召兵等[18]将杆单元和梁单元二者结合成非线性混合单元，对浮桥接头的非线性间隙的影响进行了建模求解，并对浮桥的动态响应进行了分析。Wang等[19-20]对波浪作用下的带式舟桥的水弹性响应和移动荷载作用下浮桥动态响应进行了相关研究。王丙等[21]对带式浮桥在移动荷载作用下的动力响应进行了分析，得到了不带铰浮桥与带铰浮桥荷载、速度与内力的关系曲线。

但对于浮桥纵向连接间隙的理论计算方法研究较少，本文推导并验证了移动荷载作用下考虑连接间隙的带式浮桥计算方法。该方法可以求解存在连接间隙的浮桥在移动荷载作用下的变位和受力，能够为浮桥设计提供相关理论指导。

1 移动荷载作用下长浮桥计算模型

1.1 弹性基础梁模型

带式浮桥设计计算时，可以将整个浮桥简化为弹性基础上的等刚度连续梁[11]。本文将连续体系长浮桥计算模型简化为无限长弹性基础梁，模型如图2所示。坐标系O′x′y′为固定坐标系，O′为基础梁上一点，其沿梁左右方向都为无限长，O′x′为沿梁方向，O′y′为垂直梁方向，竖直向下。Oxy为移动坐标系，O点为移动荷载P作用的位置，Ox为沿梁方向，Oy为垂直梁方向，竖直向下。OO′=vt，v为荷载移动的速度，t为荷载从O′运动到O的时间。

图2 弹性基础梁计算简图Fig.2 Calculation diagram of elastic foundation beam

由微分关系和力的平衡条件，受外力作用时，浮桥结构在x处的竖向变位y(x)，转角θ(x)，弯矩M(x)和剪力Q(x)的关系为

(1)

式中：EI为将浮桥简化为等截面欧拉梁后的抗弯刚度，E为弹性模量，I为浮桥横截面惯性矩；q(x)为外荷载线集度；p(x)为水对浮桥底板的压力线集度分布，由于浮桥的弹性基础符合温克尔地基假设，则p(x)=Ky(x)，K为基础梁弹性刚度。

由于受水的浮力作用，将浮桥简化为弹性基础梁后，可得基础梁刚度K为

(2)

式中：ρ为水的密度；g为重力加速度；A为单个桥脚舟的水线面面积；l为浮桥单跨长度。对于带式浮桥，由于A=Bl，B为水线面宽度，则K=ρgB.

由(1)式可得弹性基础梁静荷载作用下的变位微分方程[11]为

(3)

考虑移动荷载作用时，需要加上浮桥和浮桥垂向运动产生的附连水质量的惯性力，则可得到浮桥的动力计算方程为

(4)

式中：m为单位长度浮桥的质量mb与单位长度浮桥垂向运动产生的附连水质量mw之和，即m=mb+mw，mb=mu/l，mu为单跨桥节的质量，单位长度浮桥垂向运动产生的附连水质量的计算公式[11]为

(5)

Cv为剖面修正系数，κ为三维流动系数，ζ为浅水修正系数，Bb为浮桥宽度。

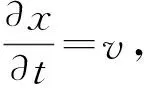
(6)

则(4)式可以化简为常系数微分方程：

(7)

1.2 长浮桥计算模型求解

由于在浮桥实际结构中，m2v4-4EIK<0总是成立[11]的，当q(x)=0时，(7)式的解为双曲三角函数，此时，浮桥会产生振动，对(7)式求解得

y(x)=e-αx(C1cosβx+C2sinβx)+
eαx(C3cosβx+C4sinβx)，

(8)

由弹性基础梁特性，利用其边界条件，可对(8)式进一步求解。

1.2.1x≥0时函数的求解

当x→∞时，y(x)→0，由于e-αx→0，eαx>0，可得

C3cosβx+C4sinβx=0.

(9)

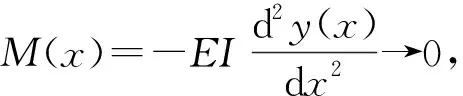
-C3cosβx+C4sinβx=0，

(10)

联立(9)式和(10)式，解得C3=C4=0.

所以，

y(x)=e-αx(C1cosβx+C2sinβx).

(11)

αC1-βC2=0.

(12)

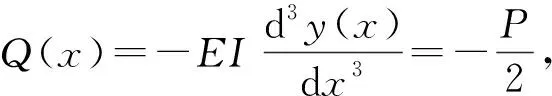
(13)

联立(12)式和(13)式，解得

(14)

将(14)式代入(11)式中，可得x≥0时，

(15)

1.2.2x<0时函数的求解

利用同样的方式，可以解得x<0时，

(16)

于是，x<0时，

(17)

可以证明：y(x)的函数图像在区间(-∞,∞)上是关于y轴对称的。为方便表示与计算，本文中的函数只表示x≥0的范围，x<0范围的函数，利用对称性求解。

由(1)式中的微分关系，x≥0时，对移动荷载作用下弹性基础梁结构的变位、转角、弯矩、剪力求解得

(18)

式中：

(19)

(19)式中函数的微分关系为

(20)

可以证明：在区间(-∞,∞)上，y(x)和M(x)关于y轴对称；θ(x)和Q(x)关于O点中心对称。本文在绘制函数图像时，只绘制x>0的范围，对于x<0范围的函数图像，利用对称性求解。绘制其变位曲线和弯矩曲线如图3和图4所示。

图3 移动荷载作用下浮桥竖向变位曲线Fig.3 Vertical displacement curve of floating bridge under moving load

图4 移动荷载作用下浮桥弯矩曲线Fig.4 Bending moment curve of floating bridge under moving load

1.3 多个集中荷载和均布荷载作用下浮桥变位和弯矩的计算

根据变位互等定理，对于无限长浮桥，浮桥上点x处的竖向变位和弯矩影响线分别和单位荷载P=1作用在点x处的变位图和弯矩图是完全一致的。根据影响线原理，计算浮桥上若干个集中荷载Pi(i=1,2,…,u)分别作用在xi(i为荷载序号，i=1,2,…,u)处时，浮桥上任意点x处的变位值和弯矩值分别为

(21)

(22)

计算均布载荷q(均布荷载的中点在点O处，长度为s)作用下，浮桥上点x(x≥0)处的变位和弯矩分别为变位影响线和弯矩影响线在区间[-s/2,s/2]的积分值，其计算结果为

(23)

(24)

浮桥上点x(x≤0)处的变位和弯矩可由对称性得到。

2 连接间隙对浮桥变位和受力的影响

2.1 连接间隙及间隙闭合区间的说明

带式浮桥纵向连接处存在间隙，间隙的存在使得桥节连接方便，同时也能适当减小桥节在外荷载作用下的结构内力。图5为带式浮桥纵向连接各间隙位置示意图，其中：间隙1为浮桥上表面承压板连接处的间隙，此处只能承受压力，不能承受拉力；间隙2为浮桥下部单双耳连接处的间隙，荷载作用下，此处主要承受拉力；间隙3处为方销，可承受纵向拉力。根据文献[15]，浮桥上表面抗拉连接件的活动间隙对浮桥最大变位和最大受力几乎没有影响。因此，本文在理论计算时只考虑间隙1和间隙2.

图5 纵向连接处的各间隙位置Fig.5 Positions of gaps at longitudinal connection

浮桥受力变形时，间隙1和间隙2闭合，桥节之间会发生转动，产生间隙角，如图6所示。图6中：γ为间隙角；Gap1为间隙1大小；Gap2为间隙2大小；h为间隙1与间隙2之间的距离。

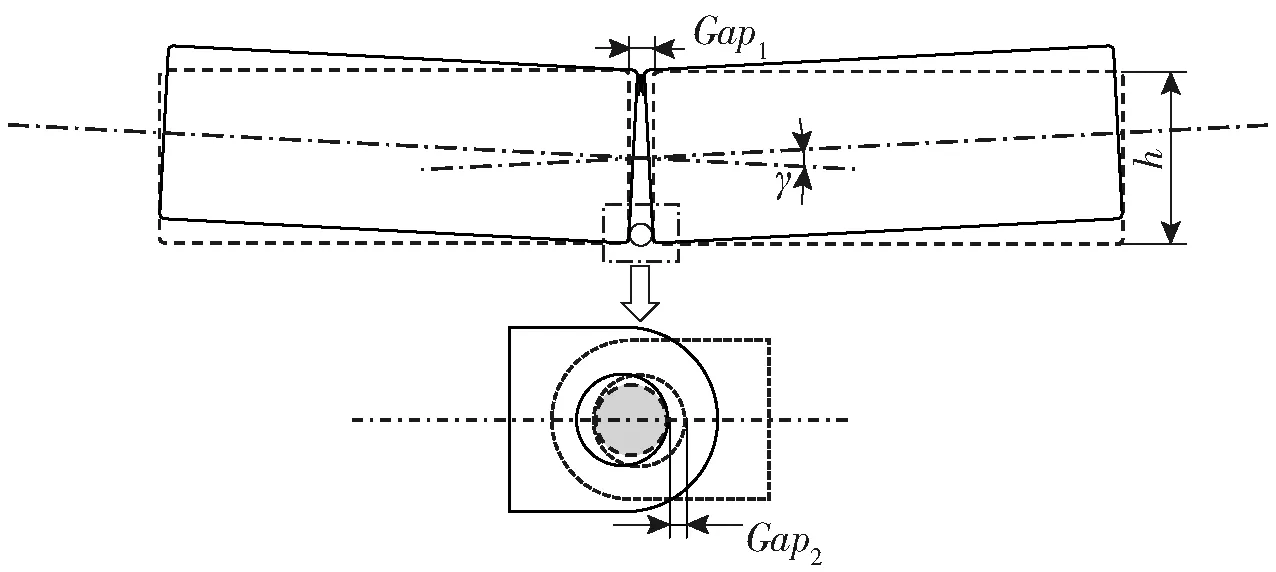
图6 间隙角示意图Fig.6 Schematic diagram of gap angle

对于带式浮桥，本文假设间隙1和间隙2对浮桥结构影响是可以叠加，则间隙角γ为

(25)

浮桥受荷载作用时，由于受静水恢复力的作用，浮桥间隙闭合的区间与荷载大小有关。但由于引起间隙角γ闭合的静水恢复力相对于荷载而言较小，暂不考虑其对间隙闭合的影响。本文假设，各连接处的间隙闭合与否根据该处弯矩值的正负而定。如图7所示，浮桥承受正弯矩的区间内间隙为闭合状态，承受负弯矩的区间内间隙为打开状态。对连接间隙分析计算时，只考虑间隙闭合区间内间隙的影响。

图7 连接间隙闭合区间Fig.7 Closed interval of connection gaps

2.2 间隙对浮桥变位和受力的影响

图8表示单位荷载P=1作用在点O时，x处的弯矩为MxO；图9表示x处发生单位转角γ=1时，点O沿y轴方向的位移为yOx. 根据功能互等定理，有

MxOγ=yOxP，

(26)

又因为P=1，γ=1，故有

(27)

图8 单位荷载与弯矩的关系图Fig.8 Relationship between unit load and bending moment

图9 单位转角与竖向变位的关系图Fig.9 Relationship between unit angle and vertical displacement

因此，图8和图9的图形形状是相同的。由图8可知，正弯矩范围为λ1，则间隙闭合区域的长度也为λ1.

由于弯矩和变位之间存在2次微分关系，弯矩与单位转角的关系可通过微分运算求出，即x处发生单位转角γ=1时，点O处的弯矩为

(28)

式中：

(29)

其与φ4(x)的微分关系为

φ′4(x)=φ5(x).

(30)

由(27)式和变位互等定理可知，点O处变位的转角影响线的形状与图9是一致的，其正值范围是λ1，如图10所示。同理，由(28)式和变位互等定理，可得点O处弯矩的转角影响线，如图11所示。

图10 变位的转角影响线Fig.10 Angle influence line of displacement

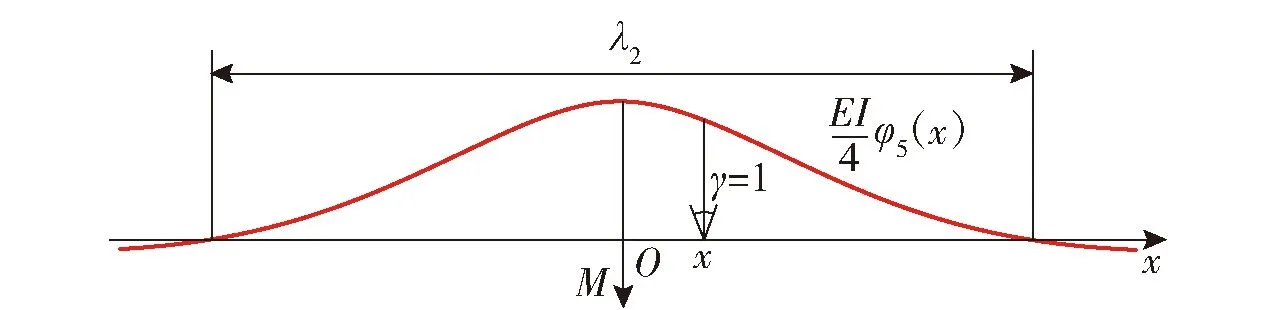
图11 弯矩的转角影响线Fig.11 Angle influence line of bending moment

得到了变位和弯矩的转角影响线，间隙角γj(j为坐标位置点的序号，j=1,2,…,k)对浮桥上点x处产生的变位和弯矩的影响值就是将间隙闭合区域范围内间隙角γj与相应的坐标位置点xj(j=1,2,…,k)处影响线坐标值相乘，并将各项叠加，即

(31)

若间隙角都相等，角度都为γ；相邻间隙角的距离等于浮桥单跨长度，长度都为l. 可近似的将间隙角γ均匀地分配在l的长度上，即间隙角集度为γ/l. 这样，就可以利用积分运算求解间隙角对变位和弯矩产生的影响值。

(32)

求解可得

(33)

(34)

间隙角对浮桥上点x(x≤0)处产生的变位和弯矩的影响值可由对称性得到。

本文在计算连接间隙对浮桥的影响时，近似地将该影响值作为一种附加值来考虑，该影响值与原有弹性基础梁计算结果叠加后得到浮桥变位和受力的最终结果，即点x处最终的变位和弯矩值分别为

(35)

式中：集中荷载作用时，y(x)和M(x)分别为yP(x)和MP(x)；均布荷载作用时，y(x)和M(x)分别为yq(x)和Mq(x).

桥节之间纵向连接处，主要是上部承压板受压力，下部销孔结构受拉力，根据弯矩和力的关系，桥节连接件部位的最终受力大小为

(36)

式中：N为上部承压板或下部销孔结构的数量；h为上、下连接位置的距离；计算下部销孔结构受力时取正号，计算承压板受力时取负号。

在荷载作用点前后一定的距离(通常为相邻第3～5个桥节处)，浮桥会出现反弯现象，此时，下部销孔受压，上部方销受拉。故下部的销孔结构既能受拉也能受压，其计算值为为正值时受拉，为负值时受压；而上部承压板只能承受压力，在反弯区间，两桥节上相对的承压板处于不接触状态，此时，上部拉力由尖舟上的方销承受，方销位于图5中间隙3的位置。因此，承压板的计算值恒为负值，对于结果为正的时候，方销受拉，两浮桥相对的承压板处于不接触状态，此时设定压力值为0.

3 数值计算与分析

3.1 参数说明

图12 浮桥的布置与荷载作用位置Fig.12 Arrangement of floating bridge and load position

为验证本文计算方法的合理性，以文献[15-16]、文献[18]中的数据为参考，与本文结果进行对比分析。其浮桥的布置、荷载作用位置如图12所示。浮桥是由15个相同的浮桥单元组成，桥节两端连接处的标号n沿x轴方向为1～16，荷载中心作用于7号测点处。

相关计算参数如表1所示，图13是浮桥横断面示意图。

表1 相关计算参数Tab.1 Relevant calculation parameters

图13 浮桥横断面示意图Fig.13 Cross section diagram of floating bridge

3.2 有限元模型的建立与求解

为验证本文方法的合理性，利用ANSYS有限元分析软件，建立了浮桥等效模型，该模型与实桥具有等效的截面刚度。在计算过程中，对弹性基础的刚度和连接间隙大小进行了等效换算，图14为一个浮桥单元的模型结构及其网格划分结果，整个浮桥模型共划分105 460个网格和280 968个节点。

图14 浮桥单元网格划分结果Fig.14 Meshing result of floating bridge unit

本文只对静荷载作用下，连接间隙分别为0 mm和5.5 mm的浮桥变位情况进行了模拟计算。模拟计算结果如图15和图16所示，两图中是将竖向变位放大了25倍的效果图。

图15 浮桥变位模拟结果(v=0 m/s, Gap1+Gap2=0 mm)Fig.15 Simulated result of floating bridge displacement (v=0 m/s, Gap1+Gap2=0 mm)

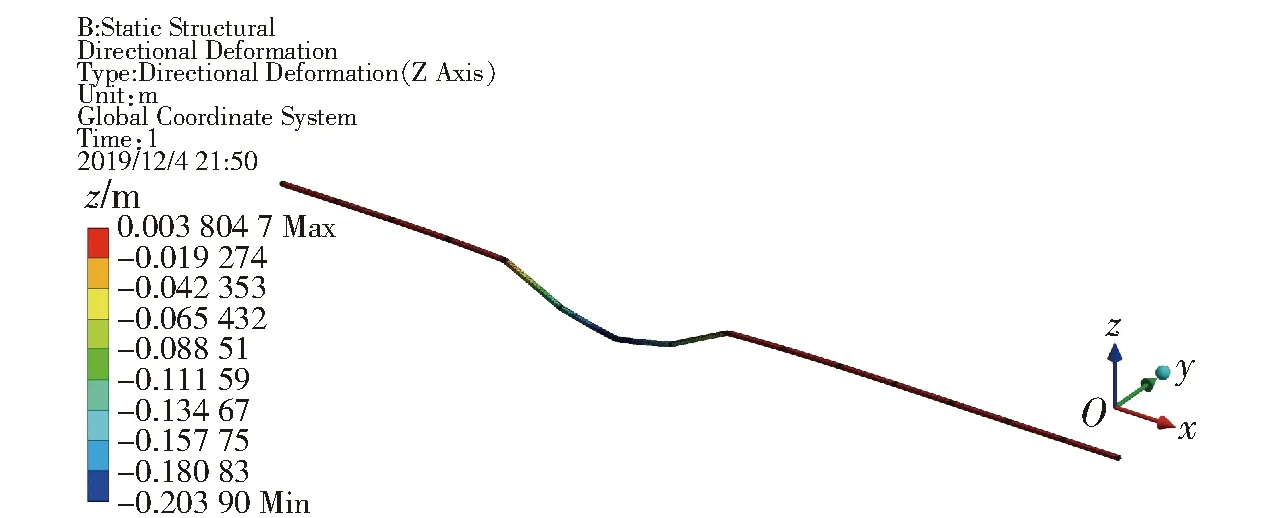
图16 浮桥变位模拟结果(v=0 m/s, Gap1+Gap2=5.5 mm)Fig.16 Simulated result of floating bridge displacement (v=0 m/s, Gap1+Gap2=5.5 mm)

3.3 结果对比与分析

由于荷载作用位置位于7号测点处，可以认为荷载作用位置两端的浮桥长度为无限长，即本文模型适用于文献[15-16]、文献[18]中的工况。下文将对各种方法计算的浮桥垂向位移和上部承压板的压力值进行分析和对比。

图17为本文方法计算的浮桥变位结果与本文有限元数值模拟结果，文献[18]中的试验值和文献[15]中数值模拟结果进行对比。间隙参数为Gap1+Gap2=5.5 mm (Gap1=4 mm，Gap2=1.5 mm)，荷载移动速度为v=0 m/s，即静荷载作用下的对比结果。

图17 静荷载作用下的浮桥变位Fig.17 Floating bridge displacement under dead load

图18为本文方法计算的浮桥连接件受力与文献[15]中数值模拟进行对比的结果。

图18 静荷载作用下的浮桥连接件受力Fig.18 Connection force of floating bridge under dead load

图19和图20分别为本文计算的浮桥变位和受力结果与参考文献[16]对比。间隙参数为Gap2=0 mm，Gap1分别为0 mm和5.5 mm，荷载移动速度v分别为3 m/s、7 m/s、10 m/s和15 m/s.

图19 移动荷载作用下的浮桥变位Fig.19 Floating bridge displacement under moving load

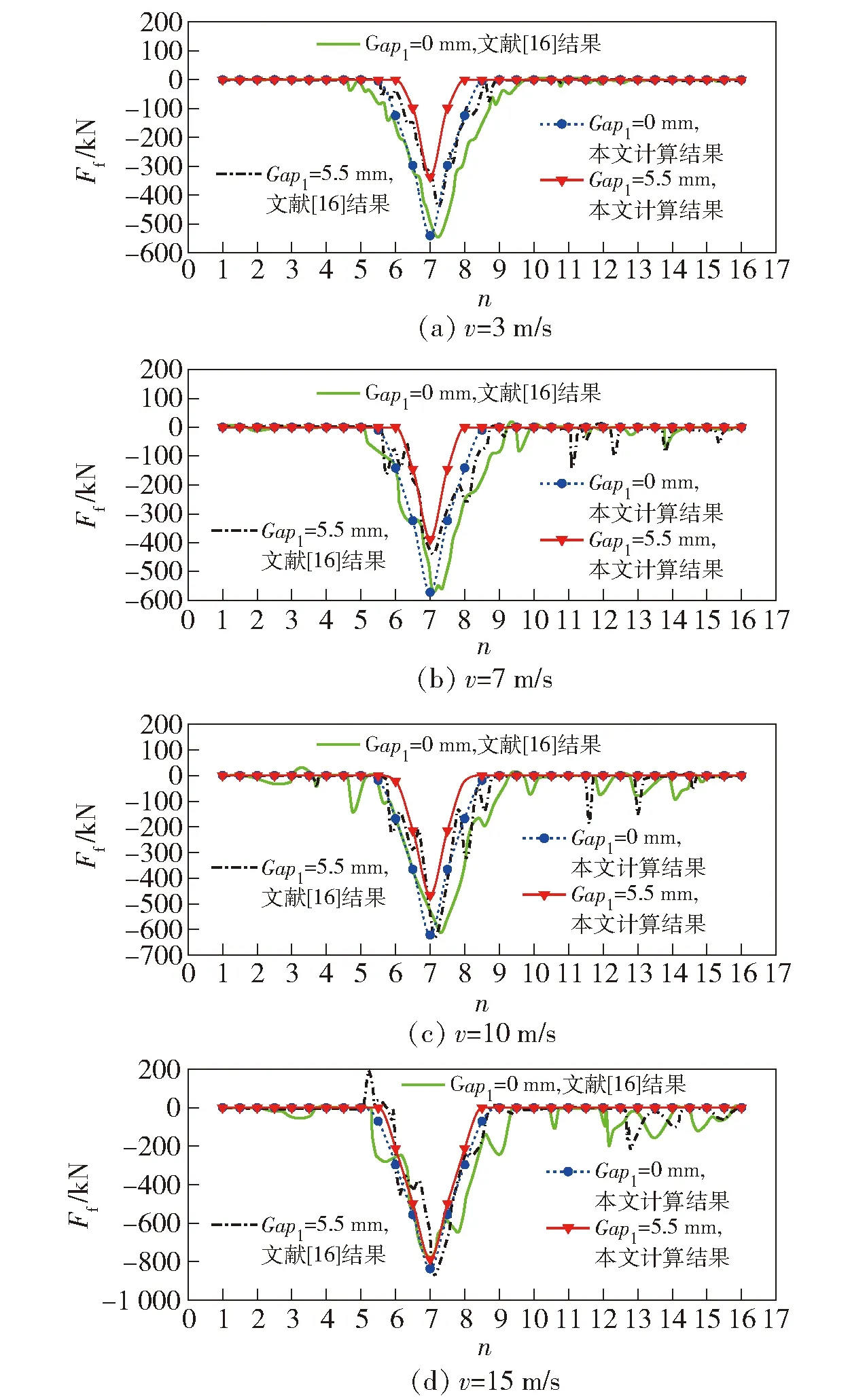
图20 移动荷载作用下的浮桥连接处受力Fig.20 Connection force of floating bridge under moving load

由图19和图20的结果可以得出，本文计算结果与文献[16]结果对比，图形的整体趋势是一致的。因此，本文基于弹性基础梁的方法来计算移动荷载作用下考虑连接间隙的浮桥是合理可靠的。

为进一步分析连接间隙和荷载移动速度对浮桥最大吃水Tmax(荷载引起的最大变位ymax与浮桥自重产生的吃水T0之和)和连接构件受力的影响，本文设定荷载为500 kN(该类浮桥最大设计通行荷载)，利用本文的方法，对比了不同间隙和不同速度的工况下浮桥的最大吃水Tmax和浮桥纵向连接部位最大受力情况。浮桥变位的最大值如图21所示，图中[T]为浮桥中心受载时的容许吃水。各工况浮桥连接处最大受力结果如图22所示。

由图21和图22可知：连接间隙的存在改变了浮桥的变位和受力状态；间隙越大，浮桥吃水增大，连接结构受力减小，车辆荷载行驶的速度对浮桥的吃水和受力有较大影响；速度越大，变位越大，浮桥连接处的受力也越大。结合前文(35)式和(36)式，可知浮桥最大吃水和受力是关于速度的递增函数。

图21 500 kN荷载作用下浮桥最大吃水Fig.21 Maximum draft of floating bridge under load of 500 kN

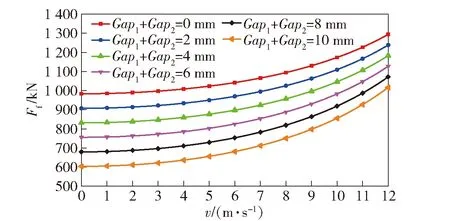
图22 500 kN荷载作用下浮桥连接结构受力图Fig.22 Maximum connection force under load of 500 kN

当荷载为浮桥设计最大通行荷载时，荷载移动速度为10 m/s时，纵向连接间隙为6 mm与间隙为0 mm计算结果对比，浮桥的最大吃水增大了9.49%，连接处接头的受力减小了16.25%；纵向连接间隙为6 mm时，荷载移动速度为10 m/s与速度为0 m/s计算结果对比，浮桥最大吃水增大了11.95%，连接处受力增大了30.02%. 由此可见，速度与间隙的影响不可忽视。

浮桥受中心荷载的情况下，通常需要保证0.1 m的干舷，故容许吃水为0.64 m. 参考图21，车速为10 m/s时，浮桥在设计时连接间隙应该控制在6 mm左右，实际情况是该类浮桥总的间隙为5.5 mm[15]. 因此，本文的理论计算结果与实际情况基本符合。