固定翼无人机多工况聚类及工况匹配
2020-09-28梁少军张世荣郑幸林冬生
梁少军,张世荣,郑幸,林冬生
(1.陆军工程大学 军械士官学校,湖北 武汉 430075; 2.武汉大学 电气与自动化学院,湖北 武汉 430072)
0 引言
目前,固定翼无人机(UAV)已在全球得到广泛应用,列装种类和数量越来越多。UAV执行任务时面临着时间紧、要求高、运行环境复杂等问题。UAV本体和外在因素决定了其可靠性,UAV一旦发生故障而坠机,会造成极大的经济损失和难以估量的军事、政治影响,故提高UAV的可靠性一直是生产厂家和用户的重点努力方向之一。UAV厂家一般配套了各子系统的自检及报警功能模块,但此类模块只能对UAV装备的健康状态作定性判断,无法准确定位故障源,更不能发现UAV的非器质性隐性故障。针对UAV的可靠性问题,国内外研究者们开展了一系列研究,并取得了一些成果[1-5]。文献[1-5]表明,在UAV故障诊断研究中,大多采用基于模型或基于多元数据统计的诊断方法,此类方法在稳态或准稳态过程中可获得较好效果,但对变工况的适应能力较差。UAV执行任务全流程包含起飞、巡航、遂行任务、返航、回收等阶段,属于典型的多工况过程,若将UAV的任务全程简单处理为一个工况,则单一模型将无法应对UAV的多工况特征,必然会导致故障漏报或误报。由此可见,UAV多工况对故障诊断影响较大,故UAV的多工况分类及工况匹配是故障诊断取得成功的必然条件。
UAV工况分类本质上是数据分组问题,解决该类问题的常用方法是聚类分析。聚类可利用数据中描述对象及其关系的信息,将数据分成不同的簇[6],是数据挖掘的常用手段。聚类算法有多种,且可以分为不同种类。其中,带噪声的密度聚类(DBSCAN)算法是一种具有噪声处理能力的划分式、互斥式、部分聚类算法。该算法通过对比局部数据的密度,寻找被低密度区域分离的高密度区域,以隔离高密度区域和低密度区域,最后将相近的高密度点连成一片,生成各种簇[7]。该算法可以在噪音数据中发现各种形状和大小不同的簇,擅长处理非球状分布数据,对噪声有较强的鲁棒性,且能够自动确定簇数。可见,DBSCAN算法适合UAV的运行数据,本文将用它来对UAV的全任务过程进行工况分析。需要说明的是,DBSCAN算法中采用欧式距离来定义密度的方法并不适合高维数据。本文将共享近邻(SNN)算法与DBSCAN算法进行结合,并提出一种新的参数寻优方案,形成一种改进型SNN-DBSCAN*算法,以适应UAV的工况特征。
UAV数据被划分为多个工况后,在线故障诊断时需要首先进行工况匹配。基于数学模型[8-9]、基于专家知识[10]以及基于数据驱动[11-12]是3类实现工况匹配的可行方法[13]。其中,前两类匹配方法都存在一定的局限性,不适合固定翼UAV的多工况分析。具体而言,基于数学模型的匹配法需要建立准确的系统解析模型,基于专家知识的匹配法则过度依靠专家经验和专业知识。而固定翼UAV的复杂性使得精确解析模型和专家知识都难以获得,限制了此两类匹配方法在固定翼UAV上的应用。基于数据驱动的匹配法则容易实现,只需获取系统的历史数据和对应的工况标签即可建立工况分类模型。就UAV而言,其运行数据可以通过数据链获得,但工况标签则无法从运行数据直观获得。
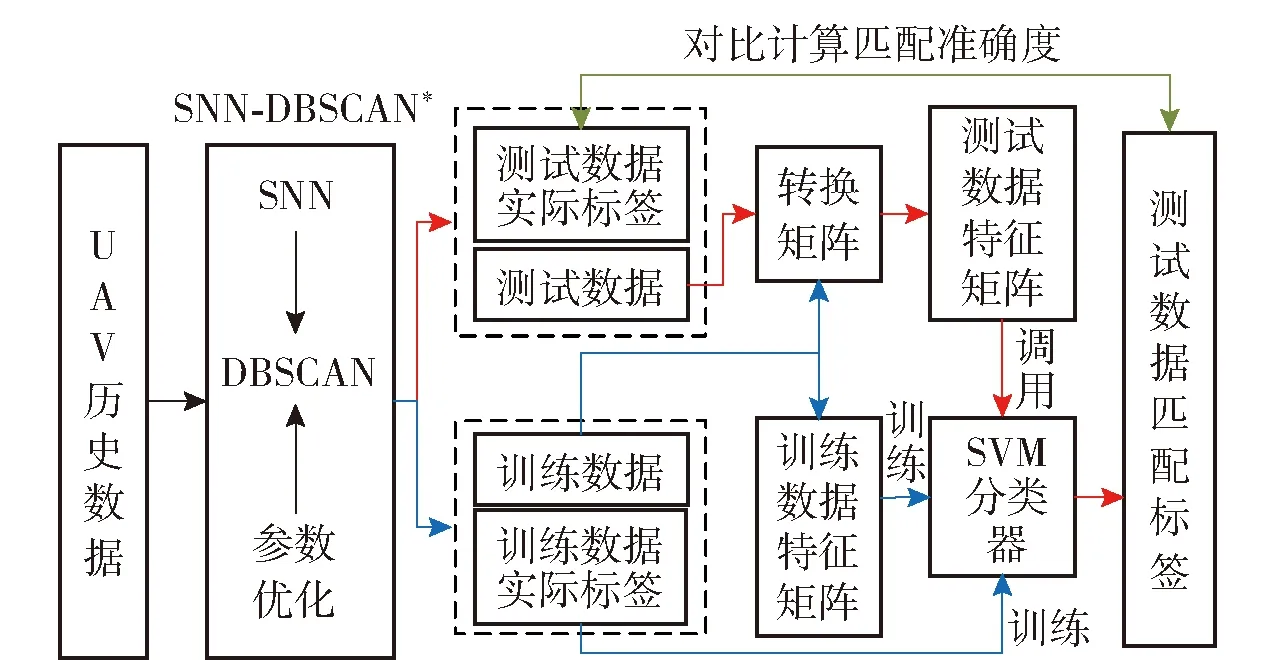
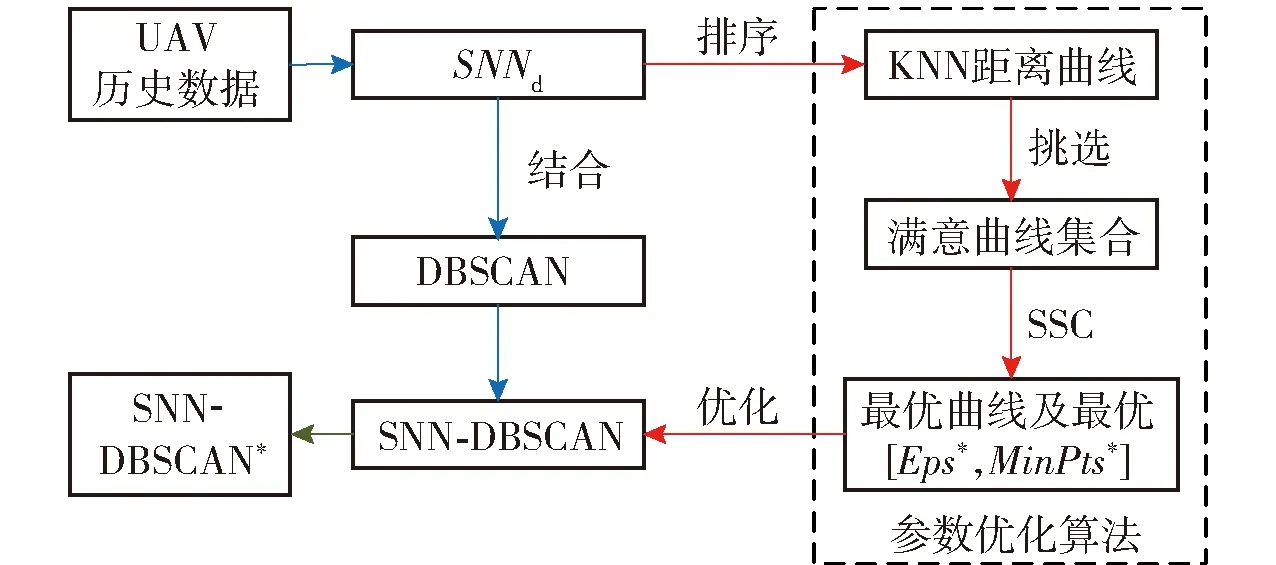
图1 固定翼UAV多工况聚类及匹配技术路线Fig.1 Mutiple working condition clustering and matching technology routes of fixed-wing UAV
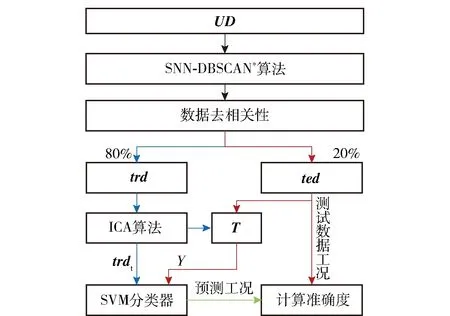
本文针对此问题,采用如图1所示的技术路线。首先获取UAV的历史飞行数据,采用SNN-DBSCAN*算法进行聚类分析,并将聚类结果作为工况标签。然后使用独立成分分析(ICA)法提取各工况的数据特征,并融合工况特征和工况标签形成工况训练样本。最后采用支持向量机(SVM)学习算法对训练样本进行学习,建立UAV工况匹配模型。在算法研究基础上,本文以某型固定翼UAV的实际飞行数据对算法进行了验证。
1 固定翼UAV工况特征
1.1 UAV操控原理
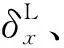

图2 无人机操控原理Fig.2 Principle of UAV control
1.2 UAV工况特征
UAV遂行任务全程一般包括起飞- 巡航- 执行任务- 返航- 回收等阶段,且各阶段会根据实时任务变动和现实情况动态调整飞机状态。不同状态下飞机传感器与执行机构反馈信息具有明显区别。图3展示了UAV执行某任务全程高度、倾斜角、俯仰角、航向角变化曲线。以图3(a)飞机高度变化为例,UAV发射起飞后迅速爬升,在升至1 000 m左右时改为平飞,之后为避障和执行任务先后两次采取爬升- 平飞- 俯冲动作以临时调整高度。在返航回收阶段,飞机总体以俯冲降高为主直至成功降落。总体来看,若仅以飞机高度变化划分工况则可分为爬升、平飞、俯冲3种工况。同样,从图3(b)飞机倾斜角变化来看,该任务全程可划分为左倾斜、右倾斜和直飞3种工况。若以图3(c)飞机俯仰角变化来看,可划分为抬头、低头和平飞3种工况。若以图3(d)飞机航向角变化来看,则可划分为左偏航、右偏航和定航3种工况。从图3(a)~图3(d)采样时间轴(横轴)综合来看,各工作状态交替出现,导致UAV工况复杂。从直观上看,无法从UAV的9维数据集中简单划分工况,甚至连工况的个数也无法获得。若仅以某参数(例如高度)为主导来处理UAV工况,将会丢失大量工况信息,造成误判。因此,本文将采用不需要先验知识的聚类算法,从数据抽象层对UAV工况进行分析。
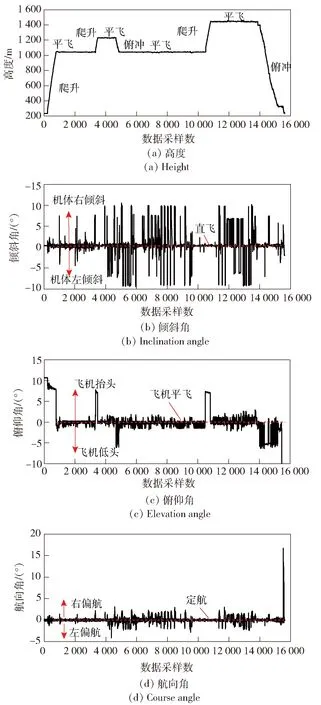
图3 UAV飞行曲线Fig.3 UAV flight curve
2 基于SNN-DBSCAN*算法的UAV工况聚类
DBSCAN算法是一种基于密度进行聚类的算法,该算法先寻找密度较高的点,然后把相近的高密度点连成一片,进而生成各种簇。DBSCAN算法以密度为指标,对噪声具有较强的鲁棒性,可基于数据自主推测聚类个数并能处理任意形状和大小的簇[14]。DBSCAN算法已经广泛应用于多个领域,如光谱分析、社会科学、土木工程、生物医学和化学等[15]。但经典DBSCAN算法需要指定核心点的最小近邻数MinPts和邻域半径Eps值,且对数据集的密度敏感,难以处理密度不均匀的数据集[16]。故经典DBSCAN算法无法直接用于UAV飞行数据分析。本文从以下两个方面对DBSCAN算法进行改进:1)引入SNN算法以提高DBSCAN算法应对密度不均匀数据集的聚类性能;2)在计算K近邻距离KNNd基础上引入数据剪切率、满意度曲线和合成轮廓系数(SSC),并提出一套分步自动优选MinPts、Eps参数方案,以降低DBSCAN算法对先验知识的依赖。
2.1 SNN-DBSCAN算法
与DBSCAN算法的密度指标不同,SNN算法采用相似度来度量两点间距离。SNN距离只依赖于两个对象共享的近邻个数,而不是这些近邻之间的实际距离,因此能够基于点的密度进行自动缩放。SNN距离反映了数据空间中点的局部结构,对密度变化和空间维度相对不敏感,可以用作新的距离度量方式来改进传统的DBSCAN算法,记为SNN-DBSCAN算法。以下将逐步介绍算法改进过程,首先从算法基本定义开始[17-19]。
在数据集空间中,若点p的Eps邻域内近邻个数大于等于MinPts,则该点定义为核心点。若点p的Eps邻域内近邻个数小于MinPts,且p落在某核心点的Eps邻域内,则该点为边界点。若点p既非核心点又非边界点,则该点为噪声点。若点q是核心点且p在q的Eps邻域内,则称p距q直接密度可达。若存在一条直接密度可达的链条p1,p2,…,pn,n为链条数据的量,且p1=q,pn=p,pi+1距pi直接密度可达,则称p距q密度可达。若在数据集D中的p点与q点的前k个最近邻中有t个近邻是共享的,则称p距q的共享近邻距离为t,并将其作为SNN距离,记为SNNd(p,q,k) =t.
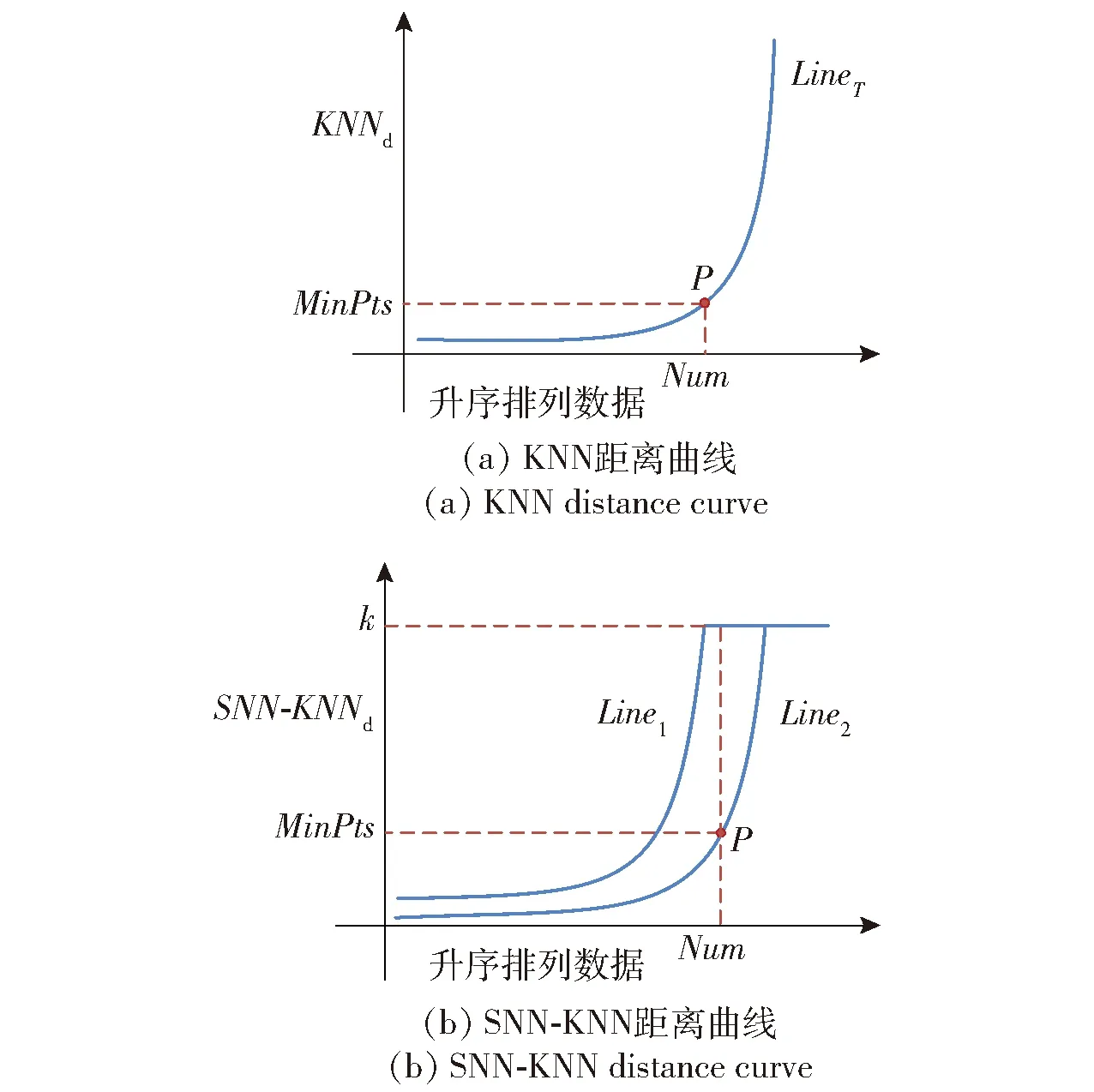
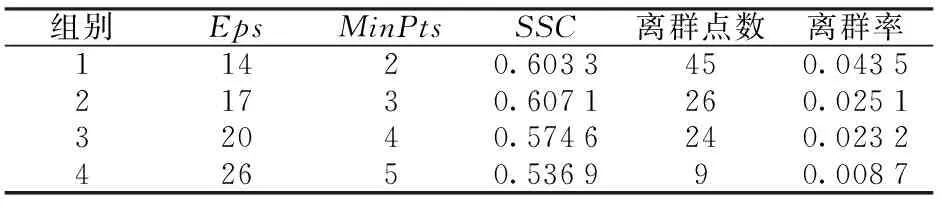
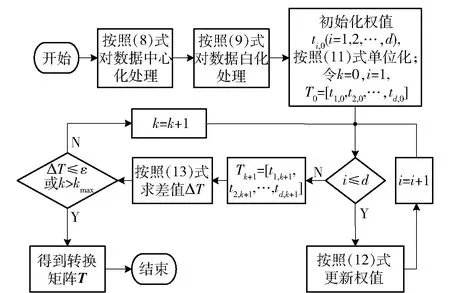
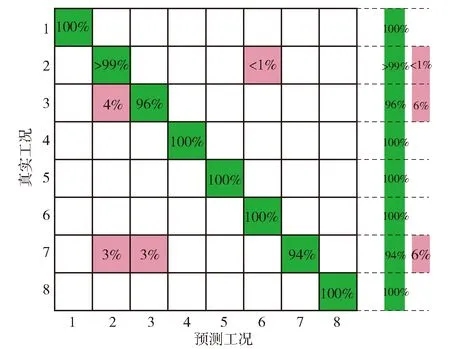
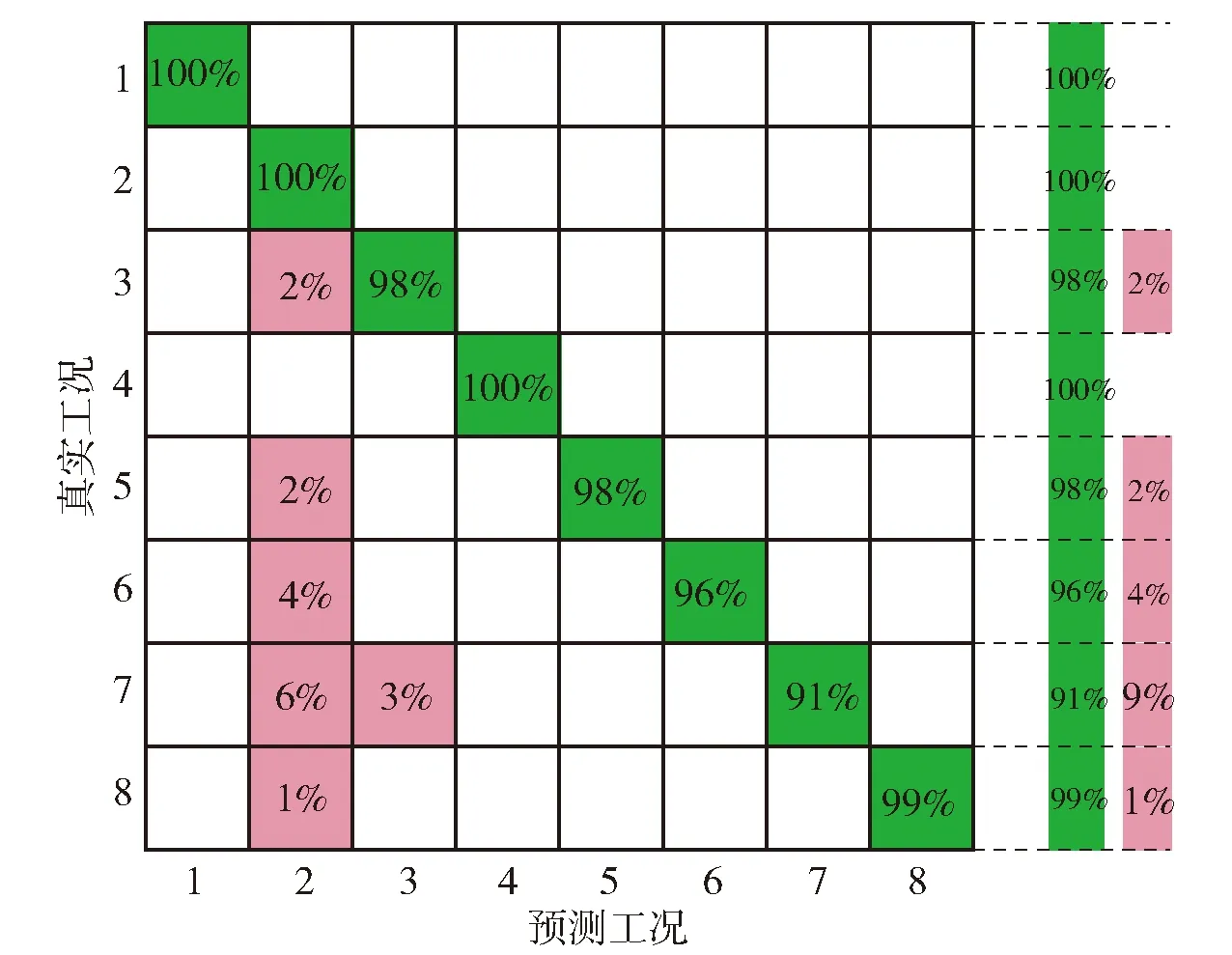
在以上SNN距离定义基础上,将SNN-DBSCAN算法用于分析UAV飞行数据,算法伪代码如图4所示,其中,Nbxi表示距离数据点xi的SNN距离不超过Eps的数据集合,|Nbxi|表示该集合的数据的量。SNN-DBSCAN算法随机选择UAV数据集中的1个点xi,利用图5所示FindN伪代码算法计算距离xi共享近邻距离不大于Eps的近邻个数|Nbxi|。若|Nbxi| Algorithm 算法1SNN-DBSCAN算法。 Algorithm Input (1)D=[x1,x2,…,xm]T∈Rm×9: 采样数据矩阵 (2)Eps: 距离半径 (3)MinPts: 阈值 (4)k: SNN近邻数量 Algorithm Output C={C1,C2,…,Ct}: UAV数据聚类集合 Algorithm Start id=1 Set allU=D//U为未处理的数据矩阵 for eachxi∈Udo |Nbxi|=FindN(xi,D,Eps,k)//根据算法2 if |Nbxi| xi∈Noise//xi判断为噪声点 else xi∈Cid//xi判断为核心点并存入对应类标聚类集合 all points inNbxi∈Cid Queue=Nbxi//Queue为过程存储数据集 whileQueue≠∅ Queue=Queue/xj//xj为Queue中任一数据 |Nbxj|=FindN(xj,D,Eps,k) //根据算法2 if |Nbxj|≥MinPts set each pointzinNbxj∈Cid ifz∈U Queue=Queue∪z end if end if U=U/xj//将xj从U中剔除 end while end if U=U/xi//将xi从U中剔除 id=id+1 end for Algorithm End 图4 SNN-DBSCAN算法 Fig.4 SNN-DBSCAN algorithm Algorithm 算法2FindN Algorithm Input (1)xi: 测试数据 (2)D=[x1,x2,…,xm]T∈Rm×9: 采样数据矩阵 (3)Eps: 距离半径 (4)k: SNN近邻数量 Algorithm Output |Nbxi| Algorithm Start |Nbxi|=0 for eachxj∈D/xido //取D中与xi不同的数据xj ifSNNd(xi,xj,k)≤Eps//根据子程序SI |Nbxi|=|Nbxi|+1 end if end for Procedure子程序:SNNd(xi,xj,k) SIxi,xj=SI(xi,D,k)∩SI(xj,D,k)//SIxi,xj即xi与xj共享近邻数量 Count=k-SIxi,xj returnCount Procedure子程序:SI(xi,D,k) Index=∅ for eachxj∈D/xido distxi,xj=‖xi-xj‖2/distxi,xj即xi与xj的欧式距离 Index=sort(distxi,xj)[1:k] //升序排序,取前k个数据 returnIndex Algorithm End 图5 FindN算法 Fig.5 FindN algorithm 在上述SNN-DBSCAN算法中,需要人为指定Eps和MinPts,其数值对聚类结果有较大影响。为了降低算法对先验知识的依赖程度,需要进一步研究Eps和MinPts的参数优化方法。 为寻找合适的[Eps,MinPts]参数组合以得到最优的聚类效果,引入KNNd和SSC概念,对SNN-DBSCAN算法进行改进。 KNNd为数据集合中每个数据点到其第T个最近邻的距离(一般为欧氏距离)[19-20]。计算D中每个数据点的KNNd距离,并将结果升序排序,即可得到K近邻(KNN)距离曲线LineT,其示意如图6(a)所示,LineT先缓慢增长后急剧上升。若取曲线拐点P处对应的KNNd和LineT为MinPts和Eps的值[21],则按照拐点启发式参数寻优思想,由此方式获得的参数组合是较优的。以该参数组合对UAV数据集进行DBSCAN算法聚类分析时,序号小于Num的所有UAV数据将会被标记为核心点,而大于Num的将被标记为边界点或噪声点。 图6 LineT距离曲线Fig.6 LineT distance curve 本文拟在SNN-DBSCAN聚类算法参数优化中采用拐点启发式寻优方法。基于SNN距离的KNNd记为SNN-KNNd,该距离度量方式会限制曲线的纵轴最大值(即0 Num=[(1-sr)m], (1) 将sr转化为新的Num值;以Num值为基准沿纵轴画一条直线与多条LineT曲线相交,若交点纵坐标满足LineT(Num)≠k则标记该曲线为满意曲线。取交点P处对应的SNN-KNNd值为MinPts值,取此点LineT值为Eps值,即可得到多对合适的备选参数组合。为了从备选组合中进一步筛选最优参数组合,下文进一步采用SSC进行分析。 轮廓系数结合了凝聚度和分离度,是聚类效果的评价指标[22]。本文根据UAV数据特征将轮廓系数与共享近邻距离融合,重新定义指标。设Xi,j表示簇j的第i个采样,Nj为簇j的样本数,C为总聚类簇集合,|C|为聚类簇总数。首先,定义凝聚度CHi,j以反映簇内部的紧凑程度: (2) 式中:CHi,j为单点凝聚度,表示Xi,j到簇j中所有点的平均SNN距离。 再定义分离度SPi,j,以反映簇与簇之间的分散程度: (3) 式中:SPi,j为单点分离度,表示Xi,j到不包含该点的簇中所有点的最小SNN距离。结合凝聚度和分离度构建SSC,以综合反映聚类效果的好坏,SSC表示为 (4) 式中:SCi,j=((SPi,j-CHi,j)/max (CHi,j,SPi,j)+1)/2,SSC∈[0,1]。在实际聚类分析中,SSC需要大于0.5,且SSC越接近1,表明聚类效果越好。在使用SSC对多个备选参数组合进行评价时,使SSC取最大值的参数即为最优组合。 引入SNNd和SSC概念后,原SNN-DBSCAN聚类算法不再需要预先人为指定Eps及MinPts值,只需给出T值的大致取值范围并预估1个可接受的数据剪切率sr即可自动优选参数,在一定程度上降低了算法对先验知识的依赖。将具有参数优选功能的SNN-DBSCAN算法记为SNN-DBSCAN*算法,图7所示为该算法的伪代码,其中Cd表示备选参数集合,Cd.MinPts表示备选MinPts参数子集,Cd.Eps表示备选Eps参数子集,SC(C)表示使用聚类集合C计算合成轮廓系数,SSCs表示存储多个合成轮廓系数的集合,Eps*表示最优Eps参数,MinPts*表示最优Minpts参数, |C|表示聚类集合C中子簇的数量,|Ci|表示序号为i的子簇内数据的量。 图8以框图形式将2.1节、2.2节提出的SNN-DBSCAN*算法原理进行了概括。SNN-DNSCAN*算法分两步实现参数寻优:1)在众多曲线中挑选出满意曲线,得到备选参数组合,并保证被选曲线有较少离群点;2)以SSC最大值为标准进一步优选备选参数组合。该算法兼顾了离群点与SSC,对数据的先验知识要求少,实用性强。 以UAV一次时长2.5 h的完整实飞数据为对象,对本文所提算法进行仿真验证,算法代码用MATLAB 2018a软件实现。UAV数据链采样周期短,完整飞行数据具有很大体量。本文旨在对UAV工况进行聚类分析,样本无需具有很高的采样速率。故先对实飞数据进行无偏差抽样,获得1 034组抽样数据构成样本集,记作trd. SNN-DBSCAN*算法的相关参数设置如下: (5) Algorithm 算法3 SNN-DBSCAN* Algorithm Input: (1)D={x1,x2,…,xm}∈Rm×9: 采样数据矩阵 (2)k: 计算SNN时最大近邻数量 (3)T: KNN参数,表示计算到第T个最近邻的距离,T∈[a,b],其中1 (4)sr: 可接受的UAV数据剪切率 Algorithm Output: Algorithm Start: T=a,KNNd=∅,Cd= ∅,SSCs=∅ for eachTin [a,b] do for eachxiinDdo KNNd=KNN(xi,T) //计算xi到其第k个最近邻的SNN距离 end for LineT=sort(KNNd) //按照升序排列,得到KNN距离曲线 ifLineT(Num) ≠k//筛选满意曲线 Cd.MinPts←T//将T值作为MinPts备选值 Cd.Eps←LineT(Num)//将KNN距离曲线在Num处值作为Eps备选值 end if T=T+1 end for for each pair of parameters inCddo//筛选最优参数组合 C=SNN-DBSCAN (D,Cd.Eps,Cd.MinPts,k)//根据算法1 SSC=SC(C)//根据子程序SSC,计算合成轮廓系数 SSCs←SSC//存入合成轮廓系数集合 end for [Eps*,MinPts*]←max(SSCs) C*=SNN-DBSCAN (D,Eps*,MinPts*,k)//根据算法1 Procedure子程序SSC=SC(C) i=1,j=1 forj≤|C| fori≤|Ci| 根据(2)式计算CHi,j 根据(3)式计算SPi,j 根据(4)式计算SCi,j i=i+1 end for j=j+1 end for 根据(4)式计算SSC Algorithm End 图7 SNN-DBSCAN*算法 Fig.7 SNN-DBSCAN*algorithm 图8 SNN-DBSCAN*算法原理框图Fig.8 Principle block diagram of SNN-DBSCAN* algorithm 图9 训练数据LineT曲线图Fig.9 LineT curve of training data 图10 UAV各工况数据三维彩色图Fig.10 3D color map of working conditiones of UAV 根据2.2节绘制LineT曲线,如图9所示。从图9中可以看出,满意曲线共有4条,分别为[2, 3, 4, 5]。故有4对备选参数组合:{[MinPts,Eps]}={[2, 14], [3, 17], [4, 20], [5, 26]}。计算各备选参数组合所对应的SSC及离群点/率,如表1所示。 表1 参数寻优结果Tab.1 Parameter optimization results 从表1中可以看出,4组备选参数的离群点率均小于5%,符合Num选定初衷。其中第2组数据拥有最大SSC值,因此最优参数为Eps=17,MinPts=3. 确定最优参数组合后,用SNN-DBSCAN*算法对UAV实飞数据集(部分变量的数据趋势曲线见图3)进行聚类分析,trd最终聚为8个簇,即8种工况,各工况三维聚类彩色图如图10所示。 图10所示的三维彩色图是一种高维数据可视化方法,该坐标系中横轴为变量维度(9维),纵轴为采样数,竖轴为归一化后的变量幅值。一次采样数据在横轴、竖轴中以一条连接各维度幅值的折线表示,折线走势代表了当下采样数据的特征。通过增加采样维度(纵轴)将聚类得到的一种工况所有采样数据对应折线绘制在一起,即可得到该工况的三维彩色图。对比图10(a)~图10(h),结合三维彩色图绘图原理及凝聚度、分离度定义可知,各工况内部采样数据曲线走势一致,凝聚度高,各工况间数据曲线走势明显不同,分离度大。可见SNN-DBSCAN*算法在UAV数据上聚类效果良好。 针对UAV的多工况特征,在线故障诊断时需要先匹配工况,才能采用对应的模型进行故障诊断。本文基于数据研究UAV工况的匹配问题,只需获取系统的历史数据和对应的工况标签即可建立工况匹配模型。第2节SNN-DBSCAN*算法完成了UAV数据的聚类,聚类结果即可作为UAV的工况标签。以下将采用ICA算法和SVM算法来实现数据的特征提取并建立匹配模型。 ICA算法是一种盲源信号分离新方法,用来从多维统计数据中寻找隐含因素或成分[23]。在UAV实飞过程中,实时采集的9个变量包含噪声和干扰,这将降低UAV工况识别的准确率,甚至给出错误结果。使用ICA算法对UAV各变量数据进行特征提取与重构,再用转换得到的特征数据代替源数据训练SVM分类器,能有效提高算法在受干扰数据下的工况匹配准确度。 设D为采样数据矩阵,A为由噪声和干扰引起的混合矩阵,矩阵S为UAV源数据矩阵,则 (6) 式中:A=[a1,a2,…,am]。 对D进行ICA得到转换矩阵T,之后通过(7)式提取特征矩阵Y,并用Y代替D用作工况模式识别,如图11所示。这是因为特征矩阵Y能在一定程度上排除噪声与干扰的影响,更能反映数据的真实特征,更逼近源数据矩阵S[24]. Y=TX. (7) 转换矩阵T可以通过FastICA法获取。该方法首先对数据D进行中心化处理,使D各维度数据均值为0,如(8)式所示: (8) 式中:E{·}表示求数学期望。之后对数据进行白化处理,如(9)式所示。白化将中心化后的数据重新表示在新的坐标系中,通过白化阵进行线性变换,在新的特征空间进行映射,映射后数据各维度之间不再有相关性且有单位方差。 (9) 式中:Rxx为中心化后数据的协方差矩阵;Λx为主对角线由Rxx的特征值组成的矩阵;Vx与特征值对应的特征向量组成的矩阵。 独立成分估计常见方法是基于极大非高斯估计原理,根据(10)式使用固定点迭代方法求线性组合yi=∑iti的非高斯局部极大值,每个极大值对应一个独立成分。该算法较多使用近似负熵作为非高斯性度量方式[24],如(10)式中的J(y)。 ti,k+1=ti,k-η[E{xg(xti,k)}-E{g′(xti,k)ti,k}], (10) 式中:y为变换后的一个独立成分;v表示标准化后的高斯随机量;G{·}可以为任意选择的非二次函数,恰当的G将有更好的鲁棒性;G1(·)、G2(·)、G3(·)为3种常用的G函数。 由于UAV观测数据D中每个样本xi具有同等重要性,使用并行正交化方法将会有效降低计算损耗。该方法首先初始化权值ti,k,并按照(11)式对权值单位化: (11) 之后由ti,k构成转化矩阵Tk=[t1,k,t2,k,…,td,k],并按照(12)式更新转化矩阵: (12) 按照(13)式计算Tk与Tk+1的差值ΔT,若ΔT小于截止阈值ε或达到最大迭代次数kmax,则算法终止,最后一次迭代输出为最终转换矩阵T,否则重复更新转化矩阵,直到算法终止。 (13) 以上FastICA算法可概括为流程图,如图12所示。 图12 FastICA法获取转换矩阵T流程Fig.12 Flow chart of FastICA method to obtain the transformation matrix T 为验证工况匹配效果,从SNN-DBSCAN*算法聚类结果中无偏差抽样20%数据,作为输入数据UD,无偏差抽取UD各工况中80%的数据构成训练数据集trd,剩余20%作为测试数据集ted. 对训练数据进行ICA,得到转换矩阵T和转换后的特征矩阵trdt. 使用trdt训练SVM非线性工况匹配器,借助T将ted转换为特征矩阵Y. 使用训练好的匹配器模型对特征数据Y做工况匹配预测,并与真实工况类标比对,计算匹配正确率,具体过程如图13所示。 图13 ICA-SVM工况匹配器工作流程Fig.13 Workflow of ICA-SVM working condition matcher 3.2.1 匹配模型建模 首先,构建包含工况类标的训练数据矩阵trdl=[trdt,wl],其中wl∈[1,2,…,8]为数据采样对应的工况类标向量。 由于传统SVM只能实现二分类,本文使用一对一方式(One-vs-One)构建编码矩阵训练多个二分类器实现SVM的多分类功能,如表2所示,该矩阵每列为一个UAV工况类别,每行为一个SVM分类编码方案。 表2 One-vs-One SVM分类编码矩阵Tab.2 One-vs-One SVM classification coding matrix 图14 ICA-SVM模型工况匹配效果混淆矩阵Fig.14 Confusion matrix of working condition matching effect of ICA-SVM model 为了验证ICA-SVM模型的性能,本文采用传统SVM模型进行对比研究。以传统SVM模型在同样情况下建模,建模准确度为99%,如图15所示。 图15 SVM模型分类效果混淆矩阵Fig.15 Confusion matrix of working condition matching effect of SVM model 由图14和图15可以看出,两种模型都能很好拟合训练数据及类标规律。下面将测试以上模型在测试数据尤其是受干扰测试数据上的工况匹配能力。 3.2.2 UAV工况匹配 分别用ICA-SVM和SVM分类器模型对带类标的正常UAV测试数据做工况匹配,效果如图16和图17所示。从图16和图17中可以看出,ICA-SVM工况匹配模型能够准确匹配UAV正常测试数据的工况,匹配准确率达95.41%,略高于SVM模型的92.86%. 图16 ICA-SVM对正常测试数据工况匹配情况Fig.16 Working condition matching effect of normal test data using ICA-SVM 图17 SVM对正常测试数据工况匹配情况Fig.17 Working condition matching effect of normal test data using SVM 3.2.3 误差压力测试 由于系统本身和使用环境的复杂,UAV采样数据难免会受噪声和干扰影响。模型在噪声和干扰影响下的准确度不但是评价模型设计优劣的指标,而且是故障诊断的前提。本节在正常测试数据基础上,按照1%的步进速度在UAV数据各个变量逐步添加0~10%的正向偏差,以此模拟干扰数据。分别使用SVM和ICA-SVM工况匹配模型对受干扰数据作工况匹配验证,匹配准确度汇总如表3所示。从表3中可以看出,ICA-SVM匹配器综合准确度为88.7%,高于SVM匹配器模型83.9%的准确度。数据采样误差一般都不超过5%,故将各变量偏差率限制到≤5%更有现实参考价值。此时,ICA-SVM工况匹配模型匹配准确度均值在92%以上,远高于SVM工况匹配模型84.6%的准确度。 表3 ICA-SVM与SVM匹配准确度Tab.3 Matching accuracy of ICA-SVM and SVM 为了便于多变量分析,将各变量偏差下的性能绘制曲线如图18所示。由图18可见,UAV各变量数据在相同误差压力下,使用ICA-SVM匹配器的匹配准确度均高于SVM模型,对噪声和干扰的抗压性更好。 图18 各维度在干扰压力下工况匹配准确性Fig.18 Working condition matching accuracy of each dimension under interference pressure 本文从聚类分析的角度审视UAV状态数据,提出SNN-DBSCAN算法及该算法的超参调优方案,即SNN-DBSCAN*改进型算法,实现了UAV工况的优选。以SNN-DBSCAN*算法对某UAV实飞数据集进行聚类分析,将UAV全任务过程分为8个工况;工况内数据凝聚度高,工况间数据分离度大,聚类效果优异。在引入满意曲线和综合轮廓系数后降低了SNN-DBSCAN*算法对先验知识的依赖,体现了无监督聚类的本质要求。在UAV工况匹配研究中,针对UAV数据在噪声和干扰下工况易失配问题,提出了ICA-SVM算法,使用ICA对UAV各变量数据进行特征提取和重构以提高数据受干扰情况下的工况匹配准确度。UAV实飞数据分析表明:ICA-SVM工况匹配模型可以获得满意的匹配准确率,与传统SVM模型相比有更好的抵御UAV传感器误差的能力。 下一阶段研究拟将本文提出的工况聚类和匹配算法与UAV故障诊断算法结合,提出一整套适合固定翼UAV多工况的故障诊断算法。2.2 SNN-DBSCAN算法参数优化
2.3 UAV工况聚类仿真与分析
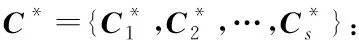
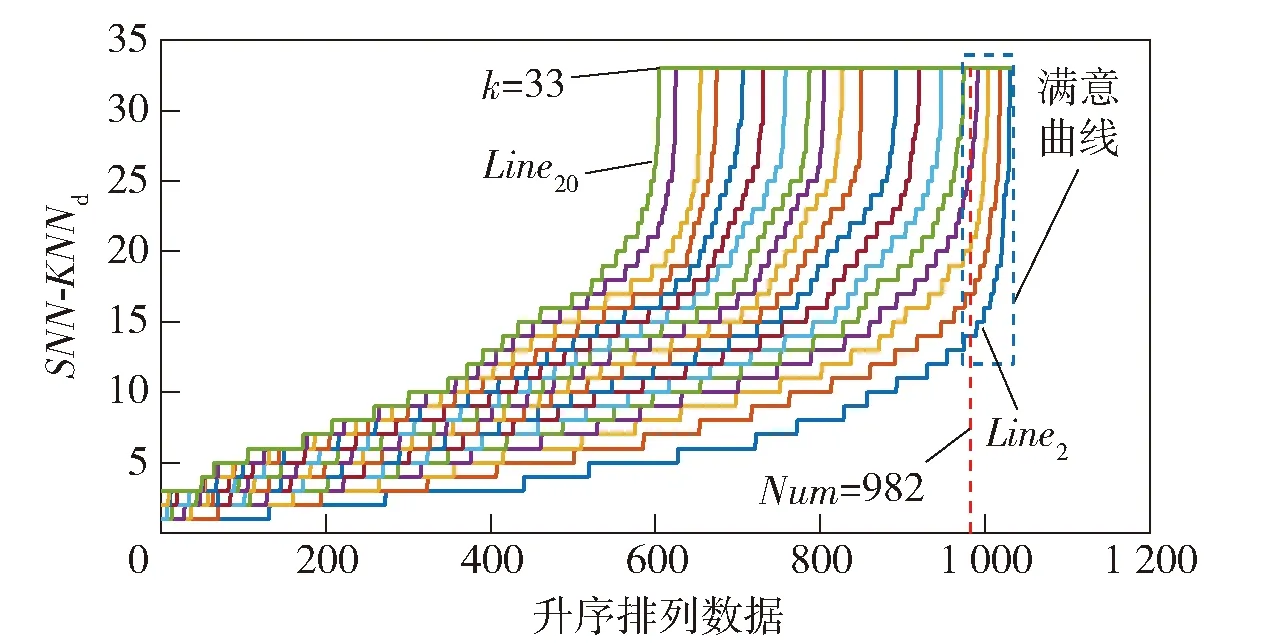
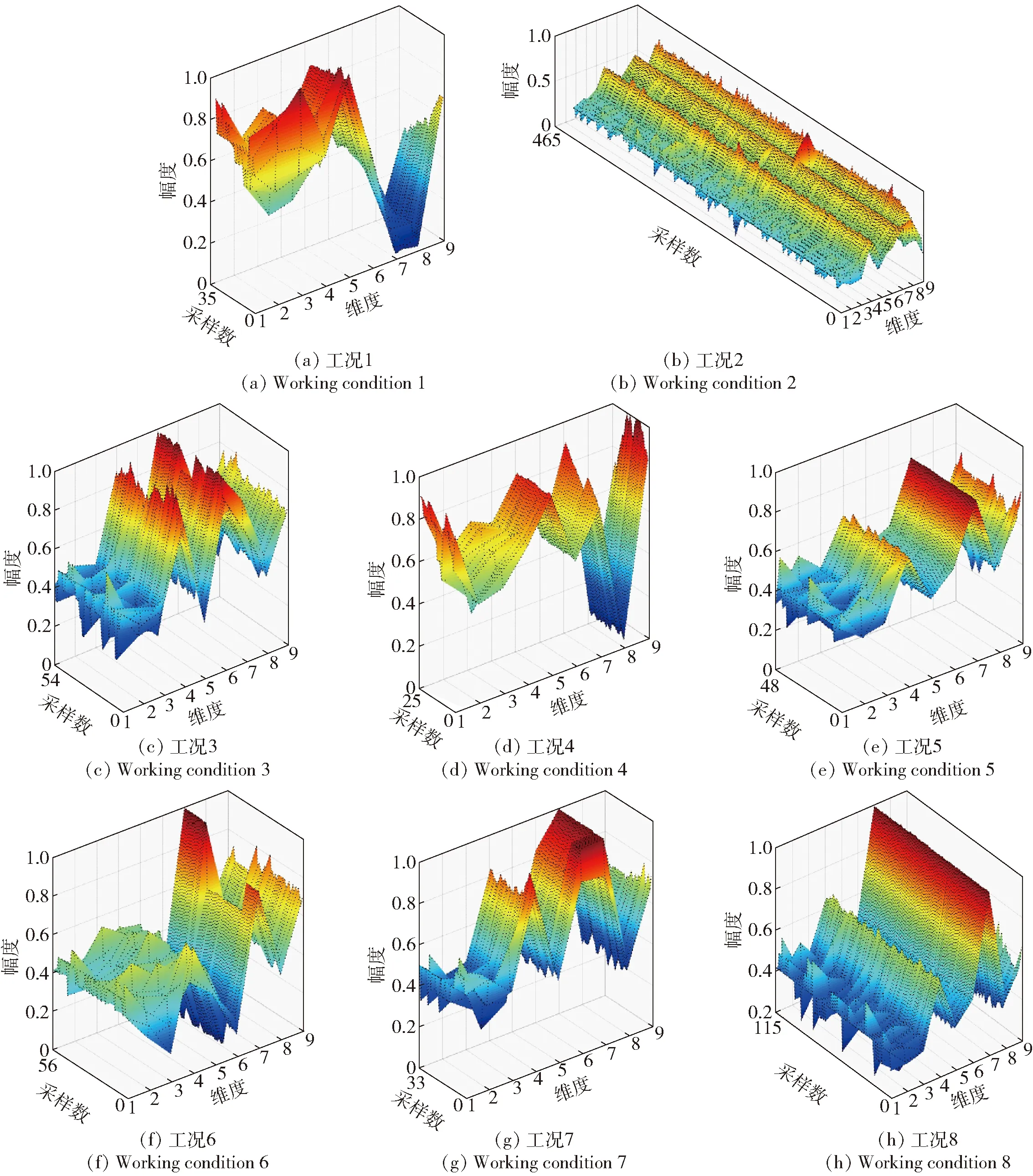
3 基于ICA-SVM的UAV工况匹配
3.1 ICA-SVM匹配算法
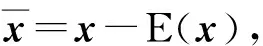
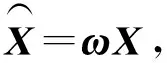
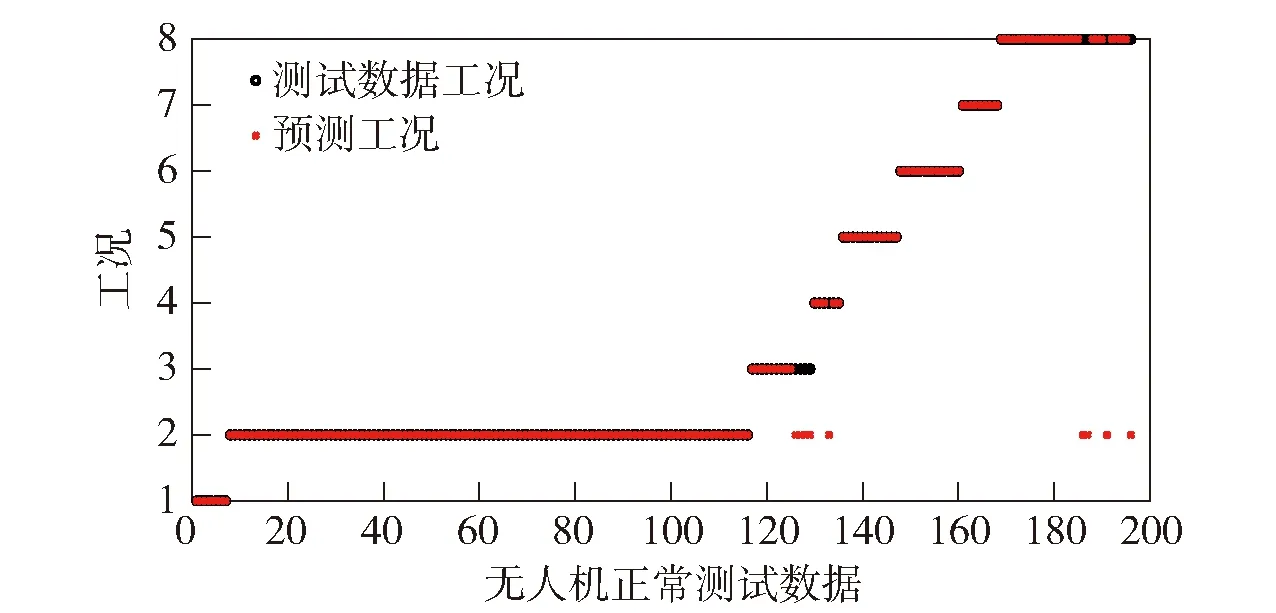
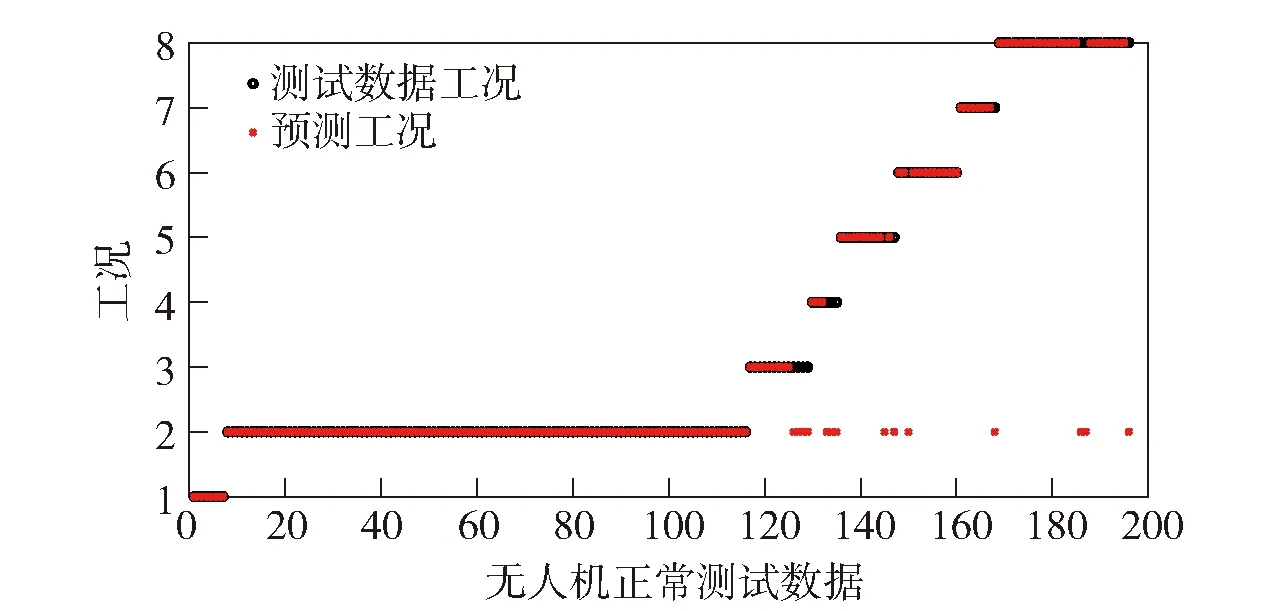
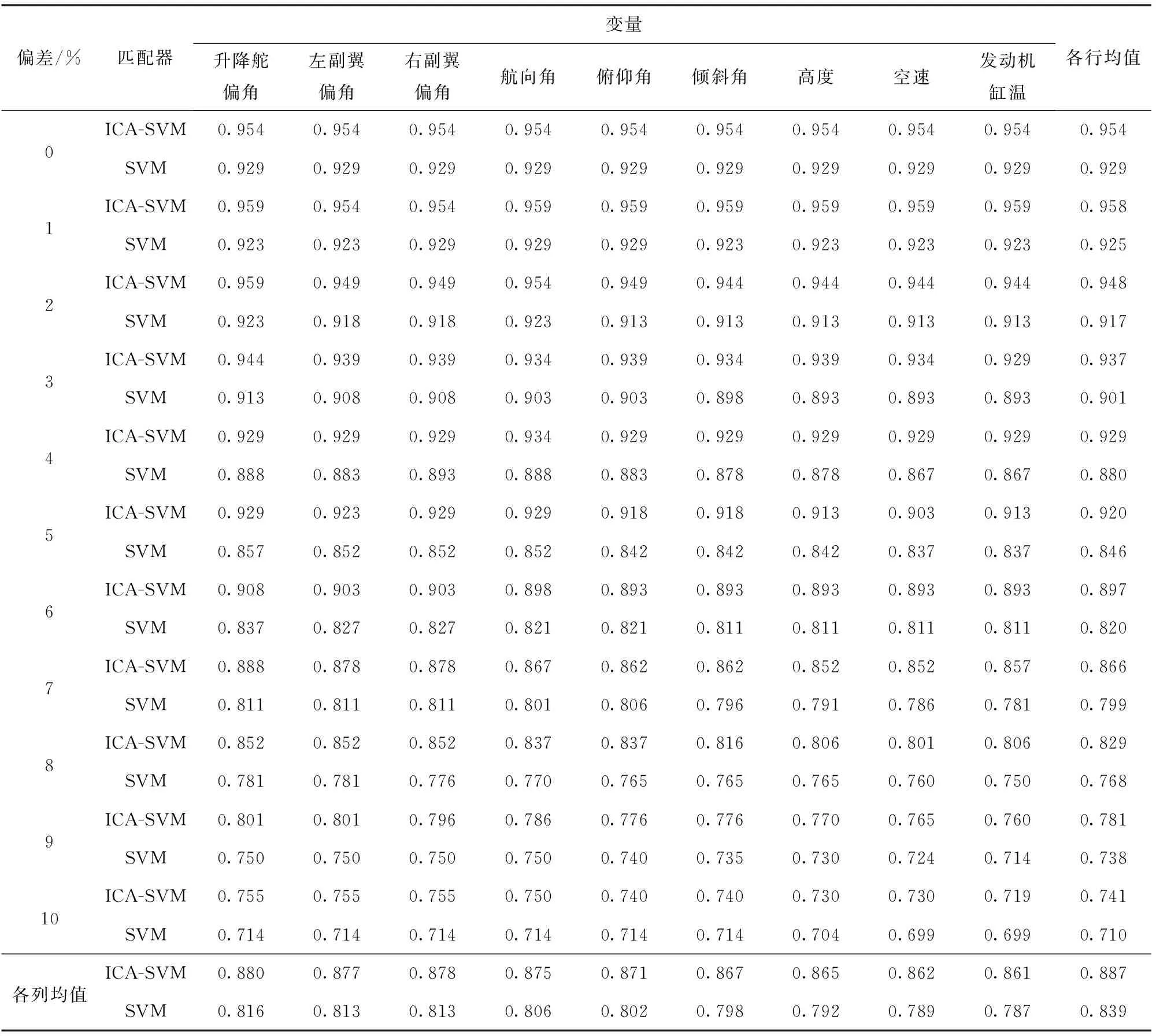
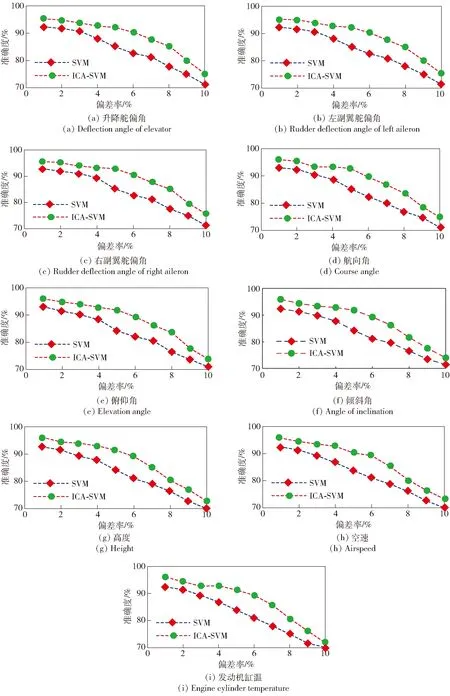
3.2 仿真与分析

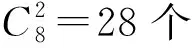
4 结论
