双侧电传动履带车辆模糊前馈- 反馈转向控制

张杰，袁东，张朋，魏曙光

(1.陆军装甲兵学院 兵器与控制系，北京 100072；2.63789部队，陕西 西安 710043)

0 引言

双侧电传动履带车辆具有机动性能良好、空间布置灵活以及燃油消耗低等优势，在现代农业和军事领域中应用非常广泛[1-5]。目前典型电传动履带车辆通常采用双侧独立电传动方案，如瑞典SEP系列、AEV系列履带车辆，美国M113A3履带车辆等[6-7]。这种方案依靠两侧履带的速度差实现车辆的转向，转向过程中受非线性动态变化的行驶阻力以及电机驱动能力等不确定因素的影响较大[8-10]，因此车辆转向控制对算法的快速跟踪和抗扰性能具有很高的要求。

目前对于双侧电传动履带车辆的转向控制研究主要有电子差速控制和直接转矩控制。在电子差速控制方面，Jarrett等[11-14]将驾驶员操控信号解析为两侧电机的转速，通过设计神经网络、自抗扰、滑模变结构等控制算法实时调整两侧电机转速差实现转向。这些方法对数学模型的依赖较大，同时车辆在越野路面行驶时负载呈现大范围、非线性和随机的特性，导致动力输出不平稳、驾驶员操控体验差。在直接转矩控制方面，邹渊等[15-18]将驾驶员操控信号解析为两侧电机目标转矩，在忽略外部扰动情况下，车辆在克服阻力后的车速和横摆角速度完全由驾驶员决定。这种控制结构易于实现，但是没有考虑方向盘转角的变化，不能快速跟踪驾驶员转向意图。同时在相同车速条件下为了实现稳定的转向轨迹，驾驶员需要不断调整方向盘来适应路面阻力的动态变化，增加了驾驶员的操控强度。

针对以上问题，本文在直接转矩控制的基础上提出一种模糊前馈- 反馈控制策略用于车辆的转向控制。通过对目标转矩的补偿和修正来提高车辆转向的快速跟踪能力和转向轨迹稳定性。采用实时仿真系统dSPACE构建硬件在环仿真平台对车辆转向的典型工况进行实时仿真实验，验证控制算法的有效性。

1 车辆总体结构及转向动力学分析

双侧电传动履带车辆的总体结构如图1所示。主要由采用发动机- 发电机组、动力电池和超级电容混合供电的综合电力系统、电驱动系统以及运动控制器组成[19]。

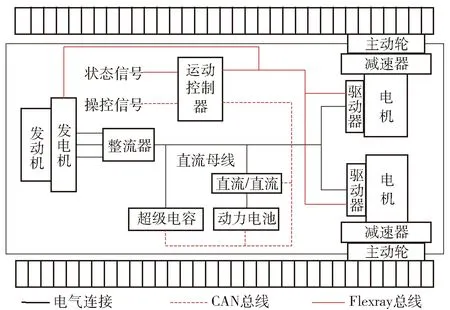
图1 双侧电传动履带车辆总体结构Fig.1 Structure of dual-motor electric drive tracked vehicle

履带车辆行驶的受力情况比较复杂，为方便分析其行驶动力学，建立受力、车辆结构参数以及运动目标之间的关系，作如下假设：

1)车辆的重心与几何中心重合；

2)忽略履带宽度的影响；

3)接地段垂向载荷均匀分布；

4)忽略地面的推土阻力、剪切阻力、迎风阻力、离心力以及履带的滑转和滑移。

履带车辆匀速转向时的受力情况如图2所示。图2中：OXY为地面参考坐标系，以车辆的几何中心C点为原点构建随动于车辆的坐标系Cxy，在初始时刻两坐标系互相重合，O′为车辆的瞬时转向中心，O′点到几何中心C点的距离为R；B和L分别为履带中心距和履带接地段长度；FL和FR分别为左右两侧电机通过减速器所提供的牵引力；Ff,L和Ff,R分别为左右两侧履带所受到的地面变形阻力；Mμ为地面对车辆的转向阻力矩；ω为车辆的转向角速度；v为车辆质心的速度；vL和vR分别为左右两侧履带的线速度。

图2 履带车辆转向受力情况Fig.2 Steering dynamics of tracked vehicle

根据履带车辆动力学理论，整车所受的外力和力矩的表达式为

(1)

式中：f为地面变形阻力系数；m为车的质量；g为重力加速度；μ为转向阻力系数；TL和TR分别为左右两侧电机输出转矩；i为传动比；r为主动轮半径；μmax为最大转向阻力系数，也就是车辆中心转向时的转向阻力系数；ρ为相对转向半径，ρ=R/0.5B.

双侧电驱动履带车辆的动力学模型可以表示为

(2)

式中：I为车辆的转动惯量。

同时车辆转向运动时满足如下的运动学关系：

(3)

2 驾驶员操控信号解析

2.1 加速踏板和制动踏板信号解析

两侧电机的目标驱动力矩之和由加速踏板和制动踏板信号直接决定，踏板结构如图3所示。图3中：φ为踏板的实时行程；φ0为踏板的自由行程，φ0=5°；φmax为踏板的最大行程，φmax=40°.

图3 加速踏板和制动踏板信号Fig.3 Structure of acceleration and braking pedals

其解析函数定义为

(4)

式中：Sb为制动标志位，当车辆处于驱动前进状态时Sb=1，当踩下制动踏板，车辆处于制动状态时Sb=-1.

2.2 方向盘信号解析

方向盘的信号用来调节两侧电机的目标转矩差，转矩差的大小以及车辆转动方向均由方向盘转角和转向决定，如图4所示。图4中：ψ为方向盘转角的实时行程；ψ0为方向盘转角的自由行程，ψ0=5°；ψmax为方向盘转角的最大行程，ψmax=85°.

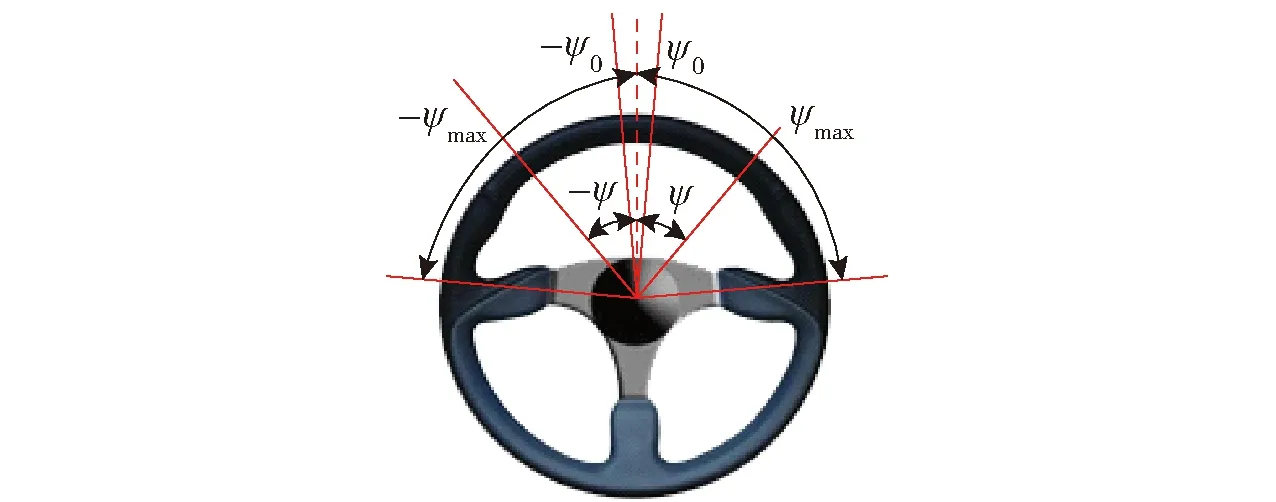
图4 方向盘信号Fig.4 Signal of steering wheel

其解析函数可以定义为

(5)

当方向盘的转角位于(-ψ0,ψ0)死区范围内时β=0，这时车辆处于直线行驶状态；当β>0时车辆右转向；当β<0时车辆左转向。

2.3 直接转矩控制策略

驾驶员通过对加速踏板、制动踏板以及方向盘的复合操作实现车辆的直线行驶和转向等工况。首先需要采用直接转矩控制策略将两侧电机目标转矩与操控信号进行关联。

(6)

式中：nL和nR分别为左右两侧电机的转速；Tmax(nL)和Tmax(nR)分别为电机在转速为nL和nR时所能输出的最大转矩。

(7)

式中：Tmin(nR)为电机在转速为nR时所输出的最小转矩。联立(6)式和(7)式可以分别得到两侧电机的目标转矩为

(8)

3 模糊前馈- 反馈控制器设计

为缩短电传动履带车辆转向的动态响应时间，更快地跟踪驾驶员转向意图，提高车辆的转向轨迹稳定性，本文采用模糊前馈- 反馈控制对两侧电机的目标转矩进行补偿修正。模糊控制不依赖于控制系统精确的数学模型，具有很强的抗扰性和鲁棒性，在复杂非线性系统中应用非常广泛[20-22]。

图5 整车转向控制策略结构图Fig.5 Structure chart of vehicular steering control strategy

3.1 模糊前馈控制器设计

履带车辆的转向分为瞬态转向阶段和稳态转向阶段。在方向盘瞬时大范围改变转角时，车辆进入瞬态转向阶段，转向半径由无穷大开始变小，直到方向盘转角、横摆角速度和转向半径不再发生变化时车辆进入稳态转向阶段。车辆的转向动态响应时间为车辆从开始转向到形成稳定的转向半径所需要的时间，因此缩短转向的动态响应时间可以使车辆更快地跟踪驾驶员转向意图进入到稳态转向阶段。通过(1)式和(2)式可以得到转向动态响应时间t为

(9)

式中：ωs为车辆稳态转向时的横摆角速度。(9)式表明适当地增大外侧电机转矩和减小内侧电机转矩能够缩短车辆转向的动态响应时间。

模糊前馈控制器采用双输入、双输出的Mamdani模糊模型。输入量方向盘转角解析函数β的论域为[0,1]，模糊子集包括S、MS、MB、B；输入量方向盘转角变化率dβ的论域为[-1,1]，模糊子集包括NB、NS、O、PS、PB；输出量kL和kR论域为[0.8,1.2]，模糊子集包括S、MS、M、MB、B. 输入和输出变量的隶属度函数如图6所示。

图6 模糊前馈输入和输出变量的隶属度函数Fig.6 Membership functions of input and output variables of fuzzy feedforward

模糊前馈补偿的控制思路应该符合驾驶员实际操控习惯和意图并满足如下原则：当方向盘转角解析函数β较小且dβ较大时，表明驾驶员发出转向指令，这时应增大外侧电机目标转矩同时减小内侧电机目标转矩；当方向盘转角解析函数β较大且dβ较小时，表明驾驶员发出回正指令，这时应减小外侧电机目标转矩同时增大内侧电机目标转矩；当方向盘dβ为0时，模糊前馈补偿的效果应该减弱。采用“Ifβ=A1and dβ=B1, thenkL=C1andkR=C2”的模糊规则形式制定前馈补偿规则表，如表1所示。

表1 模糊前馈补偿规则表(kL,kR)Tab.1 Fuzzy feedforward control rules(kL,kR)

在确定了补偿系数kL和kR以后，两侧电机的目标转矩T′L和T′R可以表示为

(10)

3.2 模糊反馈控制器设计

车辆在稳态转向时的目标转向半径通过车辆动力学公式求解时涉及大量的积分运算，严重影响了控制算法的实时性。为减少算法的计算量，同时符合驾驶员的操控习惯，根据实际需求通过大量的仿真实验结果将方向盘转角同时标定为目标转向半径，其解析函数为

(11)

式中：λ为常数，λ=7.596×10-5.

车辆进入稳态转向后，横摆角速度和车速应保持不变。这时分子中的TL+TR由加速踏板给定，当加速踏板给定信号不变时，目标转向半径R*只由两侧电机的转矩之差TL-TR决定。当车辆实际转向半径因为外界干扰出现偏差时，应该调节两侧电机的目标转矩差对实际转向半径进行修正。

图7 模糊反馈输入和输出变量的隶属度函数Fig.7 Membership functions of input and output variables of fuzzy feedback

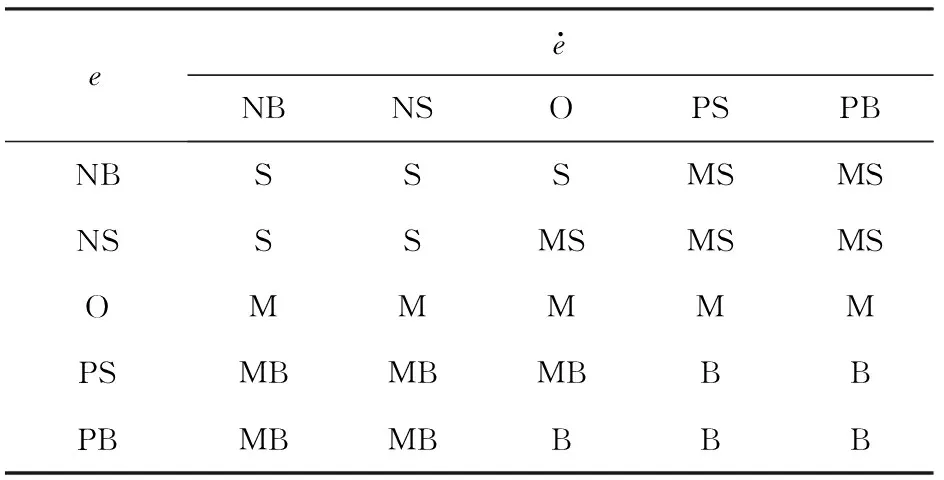
表2 模糊反馈补偿规则表(φ)Tab.2 Fuzzy feedback control rules (φ)

(12)

联立(6)式、(10)式和(12)式可以得到经过模糊前馈- 反馈控制器的补偿修正后，两侧电机的目标转矩可以表示为

(13)

4 仿真实验分析

4.1 电传动履带车辆转向控制模型

为了验证模糊前馈- 反馈控制器的性能，本文利用MATLAB/Simulink构建了电传动履带车辆转向控制模型，如图8所示。主要包括驾驶员操控模块、模糊前馈控制器、模糊反馈控制器和双侧电机驱动系统模型。

图8 电传动履带车辆转向控制模型Fig.8 Steering control model of electric drive tracked vehicle built by MATLAB/Simulink

双侧电驱动系统中电机采用面向电机输出性能建模的方式，将电机和驱动器视为一体，忽略内部复杂的电磁作用，利用主动轮电机的转矩- 转速的试验数据模拟电机的输入输出关系，如图9所示。其中电机的额定功率为80 kW，额定转矩为240 N·m，额定转速为3 200 r/min，最大转矩为480 N·m，峰值转矩为600 N·m.

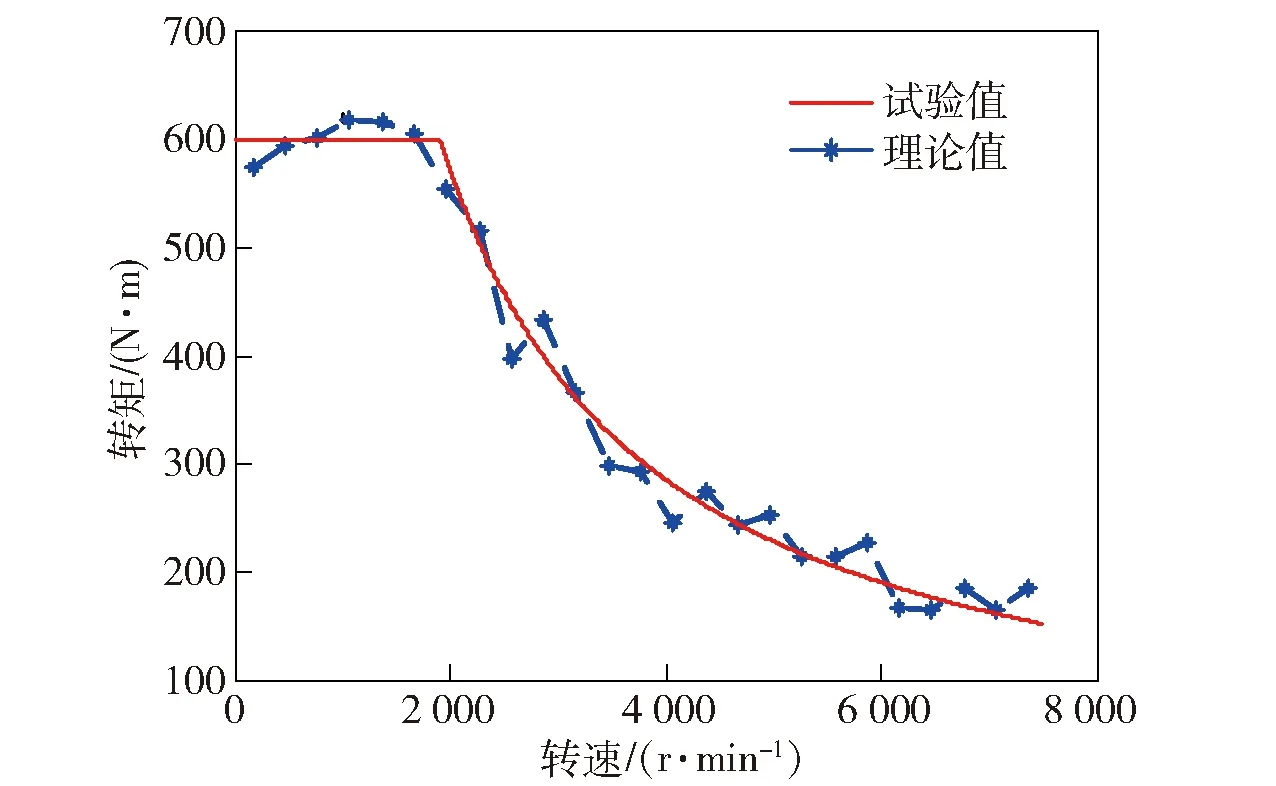
图9 主动轮电机转矩- 转速试验曲线Fig.9 Torque-speed test curve of sprocket motor

同时引入1阶惯性环节模拟电机的动态响应时间，电机最终输出转矩可以表示为

(14)

4.2 硬件在环实时仿真平台构建

为保证控制算法的实时性和可行性，便于开展设计、编写和试验于一体的控制算法快速开发，本文构建了硬件在环仿真平台对模糊前馈- 反馈转向控制策略进行实时仿真验证。

硬件在环实时仿真平台主要由上位机、dSPACE工作站、运动控制器、Vortex仿真工作台以及驾驶员操控舱等构成，如图10所示。其中上位机主要基于dSPACE平台进行控制算法的编译、下载以及采用通用实验软件Control Desk进行状态监测、参数调整，Vortex进行车辆动力学系统的仿真，各系统间通过FlexRay总线进行信息交互。借助dSPACE平台将MATLAB/Simulink中构建的模糊前馈- 反馈转向控制策略经过控制原型仿真校验后自动生成代码下载到运动控制器中。驾驶员操控舱发出的转向指令通过模拟与数字信号采样传入运动控制器，运动控制器根据转向控制策略计算得到两侧电机的输出转矩，通过FlexRay总线发送给Vortex模型车辆动力学模型，Vortex模型返回实际车辆转向半径给运动控制器完成转向控制算法的实时验证。

图10 硬件在环实时仿真平台Fig.10 Hardware-in-loop real-time simulation platform

4.3 仿真分析

以8 t重的某型电传动履带车辆为对象，车辆的仿真参数如表3所示。

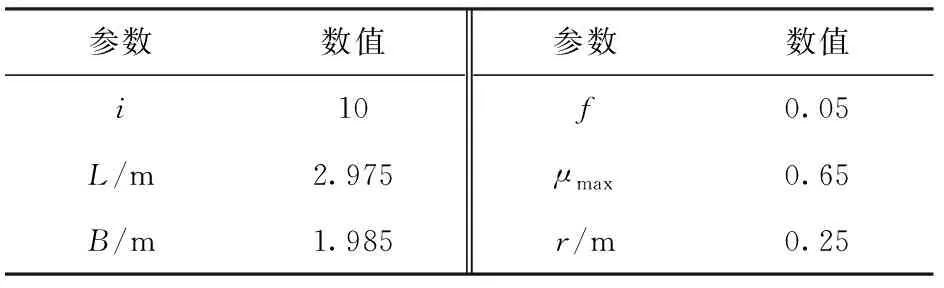
表3 车辆基本仿真参数Tab.3 Parameters of vehicle

为验证车辆转向过程中控制算法快速响应能力和抗扰性能，选取直接转矩控制和模糊前馈- 反馈转向控制分别对不同速度下的多半径转向工况进行仿真，操控信号如图11所示。

图11 驾驶员操控信号Fig.11 Driver operating signals

加速踏板在1 s时踩至行程的50%并保持到19 s，然后松开踏板至行程的25%. 方向盘在第3 s开始右转至行程的90%并保持到8 s后回正方向盘，在13.5 s时右转至行程的40%并保持到17.5 s后回正方向盘，在24 s时右转至行程的30%并保持到28 s后回正方向盘，在32.5 s时右转至行程的20%并保持到36.5 s后回正方向盘。

两侧电机的转矩和转速曲线如图12、图13和图14所示。不同速度下多半径转向仿真结果表明：当方向盘转角增大时，与直接转矩控制相比，在模糊前馈- 反馈控制下的外侧电机转矩上升和内侧电机转矩下降的趋势更快；同样当方向盘转角减小时模糊前馈- 反馈控制下的外侧电机转矩下降和内侧电机上升的趋势更快；当方向盘固定在某一位置时，模糊前馈- 反馈控制效果与直接转矩控制效果相同。从图14的电机转速曲线可以看出：在车辆瞬态转向阶段外侧电机转速增大，内侧电机转速减小形成转速差实现转向；当进入稳态转向阶段后，两侧电机转速差恒定。不同速度下多半径转向时电机的转矩和转速都能够很好地跟踪驾驶员的操控信号。

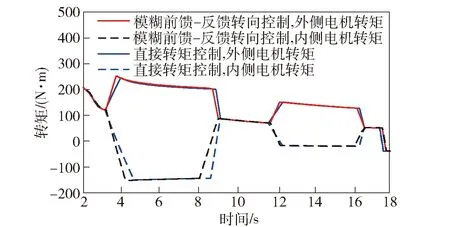
图12 高速转向时两侧电机的转矩曲线Fig.12 Torque curves of dual motors during high speed steering

图13 低速转向时两侧电机的转矩曲线Fig.13 Torque curves of dual motors during low speed steering

图14 两侧电机转速曲线Fig.14 Speed curves of dual motors

为验证模糊前馈- 反馈转向控制的抗扰能力，给最大转向阻力系数μmax增加幅值在(0.4，0.9)之间的随机扰动量，模拟路面频繁变化对车辆转向轨迹的影响。两种控制算法下转向半径的倒数仿真结果如图15所示。

图15 转向半径仿真结果Fig.15 Curves of steering radius

从图15可以看出：高速转向时的稳态转向半径分别为10B和25B，低速转向时的稳态转向半径分别为2.5B和5B. 10B转向时从3 s开始收到转向指令，在直接转矩控制策略下车辆从5.5 s开始进入稳态转向阶段，转向的动态响应时间为2.5 s；在模糊前馈- 反馈控制策略下从4.3 s开始进入稳态转向阶段，转向的动态响应时间为1.3 s，比直接转矩控制策略缩短了1.2 s. 25B转向时从13.5 s开始收到转向指令，在直接转矩控制策略下车辆从15 s开始进入稳态转向阶段，转向的动态响应时间为1.5 s；在模糊前馈- 反馈控制策略下从14.3 s开始进入稳态转向阶段，转向的动态响应时间为0.8 s，比直接转矩控制策略缩短了0.7 s. 同样得到2.5B和5B转向时的动态响应时间分别缩短了1.1 s和0.8 s. 取稳态转向阶段分析，模糊前馈- 反馈控制策略下的稳态转向半径抖振明显小于直接转矩控制，有效地削弱了外部扰动对车辆轨迹的影响，提高了车辆转向的稳定性。

5 结论

本文针对双侧电传动履带车辆提出了一种模糊前馈- 反馈转向控制策略，通过模糊控制算法将方向盘转角及其变化率转化为两侧电机目标转矩的补偿系数构成前馈控制；将转向半径偏差及其变化率转化为目标转矩差的修正系数构成反馈控制。基于dSPACE平台构建的硬件在环平台实时仿真结果表明，采用该控制算法能够有效缩短转向动态响应时间，快速跟踪驾驶员操控意图，且在路面阻力扰动下转向半径抖振大大减小，提高了车辆转向轨迹稳定性。