解析突破，思维导引，教学微设

陈宣新

[摘  要] 在教学中需要借助考题来提升学生的综合能力，解析几何题能够全面考查学生的知识水平和思维能力.解析几何题的综合性较强，建议采用思路呈现、绘制思维导图、教学微设计的方式，通过设问引导，问题拆解来还原解题过程，文章以一道解析几何考题为例开展解题教学探讨.

[关键词] 解析几何;综合;平行四边形;思维导图;思维

解析几何是高中数学的核心内容，也是高考压轴题的命题点，常以综合题的形式出现. 笔者认为提高学生解决解析几何问题的能力，应从解题策略讲解入手，帮助学生形成正确的解题思维. 因此在考题教学中应立足问题考点，解构问题思维，开展问题反思，提炼数学思想.下面以一道解析几何考题为例进行探究.

考题呈现

例题：已知椭圆C的解析式为9x2+y2=m2（m>0），直线l不经过原点O，且不与坐标轴相平行，设直线l与椭圆C的两个交点分别为A和B，点M为线段AB的中点，试回答下列问题.

（1）连接OM，试证明直线OM的斜率与直线l的斜率之积为定值.

（2）设直线l经过点■，m，延长线段OM，设与椭圆C的交点为点P，试分析四边形OAPB能否为平行四边形？如果能，请求出此时直线l的斜率;如果不能，请说明理由.

思路突破

第（1）问求证直线OM和l的斜率之积为定值，突破难点有两个：一是直线l的方程未知，二是点M的坐标未知.考虑到点M与点A和B的坐标相关，而点A和B是直线l与椭圆C的交点，因此问题实质就是研究直线与椭圆的相交问题，常用的策略是设而不求，韦达定理简化.因此求解时可以按照如下思路进行：首先设出直线l的方程，然后联立直线l与椭圆C的方程，方程的解就是点A和B的横坐标值，然后利用韦达定理构建点M的坐标，从而求出直线OM的斜率，最后对两直线斜率之积进行化简即可.

设直线l的方程为y=kx+b（k和b均不为0），点A（x1，y1），B（x2，y2），则点M■，■. 联立直线l与椭圆C的方程：y=kx+b，9x2+y2=m2，消去y，整理可得（k2+9）x2+2kbx+b2-m2=0，结合韦达定理，xM=■=■，yM=kxM+b=■.直线OM的斜率可表示为-■，所以两直线的斜率之积kOM·k=-■·k=-9，即直线OM的斜率与直线l的斜率之积为定值-9.

第（2）问分析四边形OAPB能否为平行四边形，其中点A和B为对顶点，而点P为OM延长线与椭圆的交点，分析时需要以平行四边形的判定定理为依托，构建与点坐标相关的条件，然后分析条件是否成立，即采用“先假设，后论证”的思路.

分析平行四边形的判定定理，可将定理归为三类：一是仅与平行相关;二是涉及线平行和相等;三是对角线相互平分.考虑到解析几何的问题特点，从点坐标角度来看分析四边形的对角线是否相互平分更为容易. 因此可以按照如下思路求解：设出点P的坐标，根据“对角线相互平分的四边形为平行四边形”的判定定理可得与坐标相关的条件，然后联立直线OM与椭圆C的方程，分析是否存在这样的直线OM.

设点P的坐标为（xP，yP），若四边形OAPB为平行四边形，则AM=BM，PM=OM，其中点M为AB的中点，则只需求证点M为线段OP的中点即可.转化为坐标则必须满足xP=2xM. 联立直线OM与椭圆C的方程：y=-■x，9x2+y2=m2，可解得xP=■. 将点■，m代入直线l的方程中，可解得b=■，结合（1）问可知xM=■=■，于是有■=■，从而可解得k1=4-■，k2=4+■.所以当直线l的斜率为4-■或4+■时，四边形OAPB为平行四边形.

解后反思

上述是以椭圆与直线相交为背景的解析几何综合题，问题分为两问，求证斜率之积是否为定值、探究四边形是否为平行四边形. 完成思路突破后还需引导学生对其进行反思，总结解题突破口，构建思维导图，形成系统的解题思路.

1. 挖掘问题缺口

两问均是解析几何常见的问题类型：定值问题和存在性问题. 问题以椭圆的方程为背景，求证两直线的斜率为定值，需要依托点的坐标来构建直线的斜率，故解题的突破口是联立直线与椭圆的方程，根据韦达定理来转化出点M的坐标;而第（2）问求证四边形为平行四边形，其判定定理有很多，难点在于如何选用定理及简捷提取成立条件，故解题的突破口是根据解析几何问题的点坐标特性，从对角线平分中提取与坐标相关的条件.

2. 构建思维导图

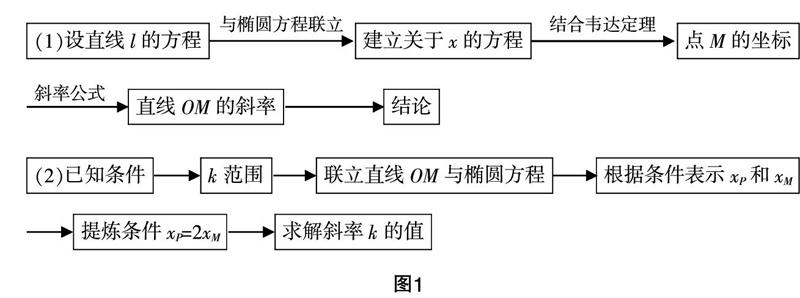
从解题过程来看，运算过程较为简洁，实则是问题分析充分到位，所构思路清晰，取得了直切主体的效果. 因此求解解析几何问题时需要重点关注解题思路的构建，在解题教学中需要构建相应的思维导图，利用图式来引导学生思考问题，培养学生正确的解题思维.以上述考题的两问为例，可以构建图1所示的思维导图.

教学微设计

解题教学中需要利用考题的代表性来指导学生掌握问题的分析方法，形成相应的解题思维，除了可以构建相应的思维导图外，还可以基于考题进行教学微设计. 微设计的过程中需要对考题进行拆解，逐步引导学生思考，掌握合理的分析步骤.

环节（一）——审题读题，信息处理

已知椭圆C的解析式为9x2+y2=m2（m>0），直线l不经过原点O，且不与坐标轴相平行，设直线l与椭圆C相交于点A和B，点M为线段AB的中点，根据题干信息来绘制草图.

意图与分析：该环节主要是引导学生来提取题干中的关键信息，根据信息来绘制草图，充分理解题干的信息条件，也是为后续数形结合辅助思考打下基础，这也是解析几何问题常用的解析策略.

環节（二）——拾级而上，引导审问

设直线l的方程为y=kx+b（k和b均不为0），点A（x1，y1），B（x2，y2），试回答下列问题.