注重概念本质，形成知识体系

邹晓松

[摘  要] 自新课改教学标准出台以来，高考更加注重核心素养的考查和理解，试卷更加重视关注数学概念本质的理解，注重数学问题的转化. 其中，高考试卷非常关注教材中的一些核心概念，这也为教学提供了一些放心，体现了新课标对提升核心素养和关键能力的要求. 因此高中数学教师在展开复习的过程中不仅要抓住基本概念，更要提炼教材中的关键内容，灵活运用好数学教材，发展学生的数学思维，使他们在考场上能更好地应对数学考试.

[关键词] 概念本质;知识体系;椭圆的概念;复习

在高中数学复习过程中，教师要注重数学中的基本概念，引导学生挖掘与之相关的数学知识，深化对概念的理解，揭示概念的丰富内涵，要能对概念进行拓展，从而形成网络化的知识体系. 概念的教学要引导学生进行总结概括，发散他们的数学思维，从中体会到概念的本质. 因此，概念的复习课不能仅靠“题海战术”，而是要把基础知识与例题再梳理，把散落于教材中的知识点进行整合、串联起来，引导学生建构起数学知识体系，从而体现出数学“源于教材，高于教材”的理念. 下面，笔者以“椭圆的概念”复习为例展开探讨，希望对大家有所帮助.

厘清概念本质

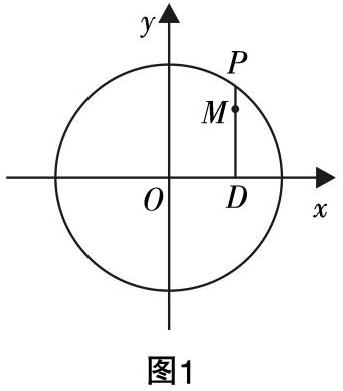
在数学教材中，各个版本对椭圆定义描述基本一致，学生一般都能牢记椭圆的定义，但在复习中要注意以下几点：（1）定义中的文字翻译成数学语言，表示为PF1+PF2=2a（2a>F1F2），那么与之对应的图形又是什么呢？（2）定义中为何要规定2a>F1F2？如果2a=F1F2，2a

在人教版数学教材中，其中有这样一道试题：

例1：如果点M（x，y）在运动过程中，总是满足关系式■+■=10，点M的轨迹是什么曲线？为什么？写出它的方程.

如果能够掌握椭圆定义的本质，学生可以快速判断和解答本道试题，这就避免了用移项再平方的方法来化解方程，降低了出错的概率. 在本道试题中，实质就是动点M（x，y）到两个点F1（0，-3），F1（0，3）的距离之和为常数10（10>6），这个动点的轨迹就是以这两个定点为焦点的椭圆，并且2a=10，c=3，这样就能求得椭圆的方程来正确解答. 由此可知，学生如果能够掌握椭圆定义的本质，那么就能快速、正确地解答出试题答案.

挖掘其他形式

1. 圆变化得到椭圆

在教学中，有的学生也会疑惑椭圆与圆之间在数学上有何关系，这一点在教材上并没有体现. 但是，在学习探究过程中，椭圆与圆之间存在着这样的结论：在竖直或水平方向上同时均匀压缩或均匀拉伸后，所得的图形是椭圆. 根据这一结论，学生能够抽象概括出问题的本质，即椭圆的生产方法是圆沿着某个方向压缩或拉伸后所得.

例2：在2011年，陕西省高考数学试卷（理科）已有所体现. 试题如下：如图1，设P点是x2+y2=25上的动点，点D是P在x轴上的投影，M为PD上的一点，且MD=■PD.

（1）当P在圆上运动时，求点M的轨迹C的方程;

（2）略.

2. 过定点的直线斜率积为定值

例3：已知△ABC的两个顶点A，B的坐标分别为（-6，0），（6，0），AC，BC所在的直线斜率（假设直线斜率存在）之积为-■，求顶点C的轨迹方程.

学生根据题目的信息很容易得到C的轨迹方程为■+■=1（y≠0），点C的轨迹为以BC为长轴的椭圆.

例4：已知△ABC的兩个顶点A，B的坐标分别为（-6，0），（6，0），AC，BC所在的直线斜率（假设直线斜率存在）之积为■，求顶点C的轨迹方程.

学生根据题目的信息很容易得到C的轨迹方程为■-■=1（y≠0），点C的轨迹为双曲线.

比较上述两道试题，我们发现二者之间的结构很相似，只是在直线斜率积方面相差一个负号，但得到的轨迹却完全不同. 此时，教师可以思考是否可以把上面的两道问题合二为一，上述试题是否具有一般规律，以上述试题再进行深度拓展，发展学生的数学思维，在潜移默化中帮助他们形成数学核心素养. 在此情况下，再把这道试题推广得到如下例题：

例5：已知△ABC的两个顶点A，B的坐标分别为（-a，0），（a，0），AC，BC所在的直线斜率（假设直线斜率存在）之积为-■，求顶点C的轨迹方程.

由■·■=-■，得■+■=1（y≠0）. 同理得到，若AC，BC所在的直线斜率（假设直线斜率存在）之积定值为■，则点C的轨迹为■-■=1（y≠0）.

在课堂讲解时，教师不能让学生简单解答就过去，还要引申相关知识，进行深度挖掘. 在学生完成试题之余，教师不妨把知识点再延伸到双曲线之中，拓宽他们的眼界，发散其数学思维，有效提升课堂教学的质量和效率. 这种把椭圆、双曲线知识进行类比和对比的教学极大地激发学生学习兴趣，使他们进一步认识到椭圆的概念，强化自身对椭圆定义本质的认知，避免在以后的学习中出现错误.

3. 与圆有关点的轨迹

在数学试题中，很多知识点都和圆有关，椭圆也不例外. 在圆的相关知识点中，一些与之有关的点的轨迹可以生成椭圆图形，帮助学生感受到椭圆的知识.

例6：在圆x2+y2=4上任取一点P，过P点作x轴的垂线段PD，D为垂足，当点P在圆上运动时，线段PD的中点M的轨迹是什么？

设M（x，y），P（x，2y），由M为线段PD的中点得到点M与点P间的关系式，P点在圆心为坐标原点，半径为2的圆上，由点P的坐标满足圆的方程来得到点M坐标所满足的方程，写出椭圆表达式.

例7：已知圆O1：（x+2）2+y2=3，圆O2：（x-2）2+y2=3，动圆P与圆O1内切，与圆O2外切，求圆心P的轨迹方程.

在本题中，先设出P点的坐标，根据题意找到圆P与圆O1、圆O2的半径间的关系. 根据椭圆的定义，发现点P是以O1，O2为焦点，定长为7的椭圆.

学生在解题过程中感受到椭圆定义所带来解题的便捷，但也意识到并非只有椭圆相关知识才与椭圆有关，圆的一些知识也会与椭圆相关，这有利于改变传统数学思维习惯，有效提升解题质量.

4. 与距离有关点的轨迹

例8：已知圆内的一个定点（非圆心）作圆C与已知圆相切，则圆C的圆心轨迹是（  ）

A. 圆 B. 椭圆

C. 圆或椭圆？摇？摇 D. 线段

设定点为A，已知圆的圆心为O，半径为R，动圆的圆心为C，半径为r，AC=r，OC=R-r，AC+OC=R（OA

在做完这道试题后，教师不要着急让学生接过这一知识点，还可以继续进行深度挖掘与拓展，如：（1）把“相切”变为“内切”或“外切”;（2）改变题目的信息，把定点与圆相切变为动圆与定圆相切，经过某一定点. 这种拓展的思路能有效改变学生的学习习惯，便于他们发散数学思维，提高数学课堂学习效率和质量.

值得引起注意的是，这种类型的试题在高考中曾经出现过，即2013年高考全国卷Ⅰ：已知圆M：（x+1）2+y2=1，圆N：（x-1）2+y2=9，动圆P与圆M外切并且与圆N内切，圆心P的轨迹曲线为C. 求C的方程. 学生在做这部分试题时要引起注意，避免不经意间的失分.

总结归纳定义

在高中数学复习教学中，教师讲课的目的并不单是让学生理解和掌握椭圆的概念这么简单，而是要引导他们以椭圆定义为核心，形成一个知识体系，对知识有由局部到整体、由点到面的整体认知. 在教学过程中，教师要注重从定义、拓展、实例分析等方面进行教学，紧扣“椭圆定义”这条主线来展开，引导学生在理解基础上进行思考和交流，进而抽象概括得到椭圆的定义，形成数学知识体系. 其中，最关键之处在于对概念的深入挖掘，对试题的二次开发，引导学生提炼得到椭圆这一核心概念的本质，熟悉知识点间的规律，把教材中的零散知识有机串联起来，对知识进行系统化整合以及再加工.

总之，在数学概念的复习教学中，教师一定要注重学生对核心概念的理解，不要拘泥于表面形式，要引導他们向深度发展，对数学概念能够进行延伸拓展，有效形成数学核心素养.