初中数学教学中数形结合思想的应用
2020-09-24邵文婷
邵文婷
【内容摘要】在初中阶段的数学课程中,“数”和“形”是两个重要的组成部分,通过正确的教学思路和教学方法,可以帮助学生更好地理解所学知识,实现两者之间的互通互助。因此,在数学教学中,教师要适时渗透数形结合的思想。
【关键词】初中数学 数形结合思想 教学应用
一、数形结合思想
数和形作为两个最基本的数学概念引领着数学学习,是每个学生都很有必要掌握学习方法。在教学中,数形结合也是很实用的教学方法,它可以把抽象的数学问题简单化、直观化,提升解题效率。概括地说,数形结合思想是一种解决数学问题的思想方法,它是通过分析数学问题的代数和集合意义,通过数与形的结合,运用抽象思维和形象思维解决数学问题的方法。
二、数形结合对初中数学教学的意义
1.使学生更加直观地领域数学知识
初中生在学习数学时往往存在思维能力较弱,空间想象力不足的问题,尤其是几何的学习,表现更为吃力。数形结合的方法,使复杂的数字表述关系得以简化,成为一目了然的“图形”,便于学生直观地理解数学问题。
2.数形结合能够促进学生的思维发展
数形结合思想的核心是将一些复杂、抽象的数学知识具象化处理,利用图形来表达难以理解的文字,进一步拓展学生的思维领域。这是解决数学问题的又一个思路和角度,有利于拓展学生的数学思维,做到举一反三,甚至学科间的融会贯通。
3.拓宽学生的知识视野,保证学生全方位发展
新课改下的数学教学,更加强调学生核心素养的培养,也就是加强数学学习与生活之间的链接,得以生活化的运用。数学中的数形结合思想,可以实现知识之间的迁移,让学生在处理问题时更加冷静、理智,为终生学习打下良好的基础。
三、数形结合思想在初中数学教学中的应用
1.以数助形
在数学学习中,教师要对数形结合常用的结合点进行讲解,让学生可以熟练地掌握,深化学生对数形结合的认识。在教学实践中,笔者总结了两条:一是常用到坐标和数轴,二是利用距离、面积和角度这些几何量。这两条都可以实现代数问题和几何问题的互解。
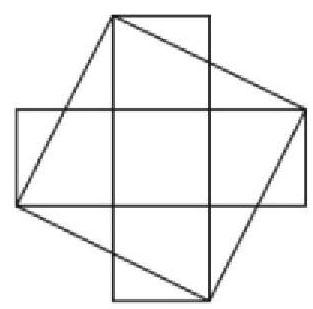
例如图一这个问题:该图形是由5个边长为1的正方形组成的,如果把图形拼接为一个正方形,那么正方形的边长是多少?如何拼接?学生们第一眼看到这个问题会认为这是一个几何问题,用“形”的角度来解决问题,通过实验操作来获得答案,但是这样很容易把问题复杂化。教师在讲解时,要引导学生进行“数”的思考。如下图所展示:
解析:针对这样的问题,可能很多学生会从“形”的角度来进行思考,应用试验操作的手段,来回答相应的提问,但是这样很有可能会使简单的问题复杂化。所以,针对这种情况,教师可以帮助学生从“数”的角度来计算问题。如图所示,学生通过面积计算得到正方形的边长为 5,那么这时需要在图中找到另外一段边长为 5的线段,以此来作出一个正方形,顺便得出裁剪的方法。
以上的解题方法,有的教师会认为是一个面积题,但是这不。是这道题最本质的东西,需要更加深入的解读。在拼接问题中,面积是一个不变的量,用面积法来对付这类拼接问题,是一个简便宜行的方法,学生也很快能够掌握。但是需要说明的是,面积本身就是从“数”而来,是对数量关系的刻画。这本身就是一种“数形结合”的思想,教师要对此作出深刻的说明,更有利于学生进行理解。
2.以形化数
根据题目画出正确的图形可以很快地突破题目中的难点,数学解题时也常常因为得到一条巧妙的辅助线,达到四两拨千斤的效果。在实际教学中,教师会常常引导学生通过画图来解决很多代数问题。
在教学实践中,以形化数可以很好地用于函数和方程的解题中,大大提升了解题效果。刚刚接触一次函数时,学生对整个概念理解起来比较困难,相关理论也感到比较陌生。但是如果在坐标系中将其显现出来,则很容易掌握了其本质。
3.数形互变
数形之间的相互转化,可以使学生更好地解決数学问题,大大提高学生的解题效率,提高数学学习兴趣。
例如,常用到的平面直角坐标系和函数,二者之间的关系可以在一个平面中得到很好地阐释。学生通过观察,会把代数问题与坐标系中的几何图形进行对应,形成一个更加直观的印象。
结束语
数形结合是一种利用数与形之间联系探究数学解题方法,总结数学规律的一种理念。初中数学是数学学习承上启下的重要阶段,但是这个阶段的学生思维能力还欠发达,需要正确的学习方法予以引导。数形结合作为数学学习的基本方法之一,值得教师花更多心思去研究和传授,帮助学生进一步促进数学思维能力的提高。
【参考文献】
[1] 刘远辉. 数形结合思想在初中数学教学中的实践研究[J]. 教学实践,2016 (10):258.
[2] 李忠华. 初中数学教学中数形结合思想的运用探讨[J]. 文理导航旬刊,2017 (20):15.
[3] 魏晓琳. 数形结合在初中数学教学中的应用[J]. 数学学习与研究,2018(22):41.
(作者单位:甘肃省合水县乐蟠初级中学)
