改进型对称四级光纤环及其制备方法

葛双超,杨瑞峰,郭晨霞

(1.中北大学仪器与电子学院,山西 太原 030051；2.山西省自动化检测装备与系统工程技术研究中心,山西 太原 030051)

1 引 言

光纤陀螺(FOG)是一种能够精确测量运动物体方位的新型惯性导航仪[1],具有检测精度高、响应速度快、抗冲击性强、体积小、重量轻等诸多优点,在低精度民用航空、高精度军用设备以及超高精度航空航天导航系统等多个领域都具有重要应用[2]。

FOG以光纤环(FOC)为核心敏感元件,由激光源发射出的光线朝两个方向沿FOC传播,通过两束光之间的相位差来测量运动物体的旋转角速度。根据Sagnac效应,FOG测量灵敏度与绕制FOC的光纤长度成正比。另外,FOC结构互易性和稳定性直接影响FOG的测量精度[3]。高水平的制环技术一直受到国外技术封锁,制约了国内光纤陀螺的研发及其应用。

环境温度发生变化时,光纤环内会产生温度梯度,进而引起沿光纤环的反向传播的两束光波之间产生相移,这种热至非互易性相移称为SHUP效应,为抑制该误差常用对称四级绕法制备光纤环。该绕法存在跨层换纤,导致边缘光纤匝易挤压变形,出现叠丝、塌陷等绕制缺陷[4]。目前有效解决这类工艺问题的方法是人工边缘控制,所以国内光纤环生产效率偏低,一台绕纤设备需要配备十几名操作者来进行过程控制和边缘调整,极大限制了高水平光纤陀螺的发展。

为解决上述问题,本文分析了边缘非对称四级FOC的SHUP误差和相位偏移,提出了自动化边缘非对称四级FOC绕制方法,并进行了实际绕环实验验证。

2 边缘非对称四级光纤环结构

对称四级绕法是Nicholas于1983年提出的[5],具有绕制方法简单、互易性高等特点,可以有效降低SHUP效应,是目前应用最广的FOC绕制方法。进行对称四级FOC绕制时,首先将待绕光纤分成长度相等的两部分,分别绕到左右供纤轮上,然后按照图1所示步骤,完成一个四级绕制,往复循环将待绕光纤全部缠绕至光纤环骨架上。

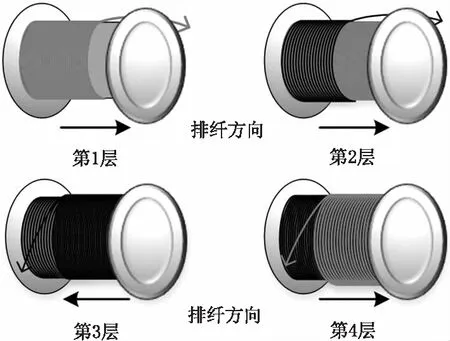
图1 对称四级结构FOC绕法示意图

对称四级光纤环的每个四级结构存在左段光纤从第1层至第4层的换成现象,两个相邻的四级结构之间存在右段光纤从第3层至第6层的换层现象,如图2所示。

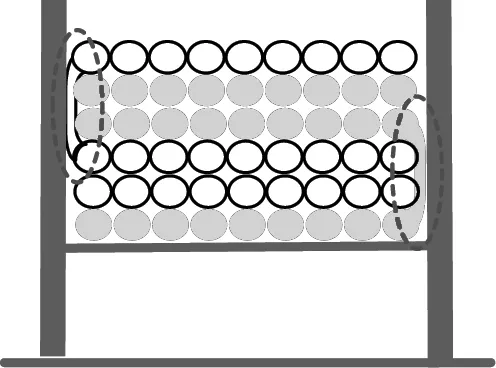
图2 对称四级结构中的换层现象

换层部分的光纤会受到骨架侧壁和内侧光纤匝的挤压,极易产生扭曲变形,形成应力奇点[6],甚至会发生剥丝现象,导致整个FOC失效。为解决该工艺问题,研究过程中采用如图3所示边缘非对称四级结构进行绕制,这种绕纤方式不存在光纤丝跨层问题,更能保证FOC的结构稳定性。

图3 边缘非对称四级结构

但是这种结构破坏了原本的对称四级性,对SHUP误差的抑制作用会产生影响。故首先对不同温度载荷下的对称四级结构和边缘非对称四级结构的SHUP误差进行分析。

3 不同温度载荷下的SHUP误差分析

3.1 SHUP误差产生机理

由于SHUP误差难以与Sagnac相移进行有效区分,所以会影响导致FOG输出准确性。

离散化SHUP效应数学模型如公式(1)所示[7]:

(1)

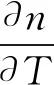
3.2 三维FOC模型

ANSYS软件是进行FOC SHUP效应分析的最常用软件[7-8]。为了实现SHUP误差精确定量分析,构建了如图4所示三维有限元模型。

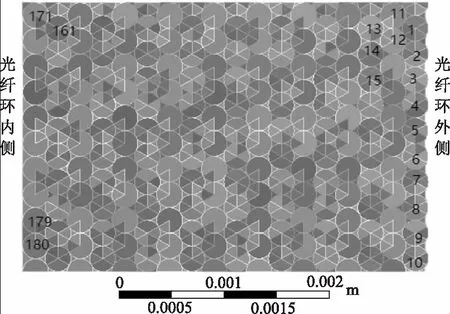
图4 FOC三维有限元模型

仿真模型中,FOC总层数为18,每层匝数40,光纤直径0.245 mm、折射率1.4685,光纤环骨架内径44 mm。

对于各种不同加载模式所用的外界温度场激励曲线均如图5所示,但是不同模式下温度加载方位有所区别。

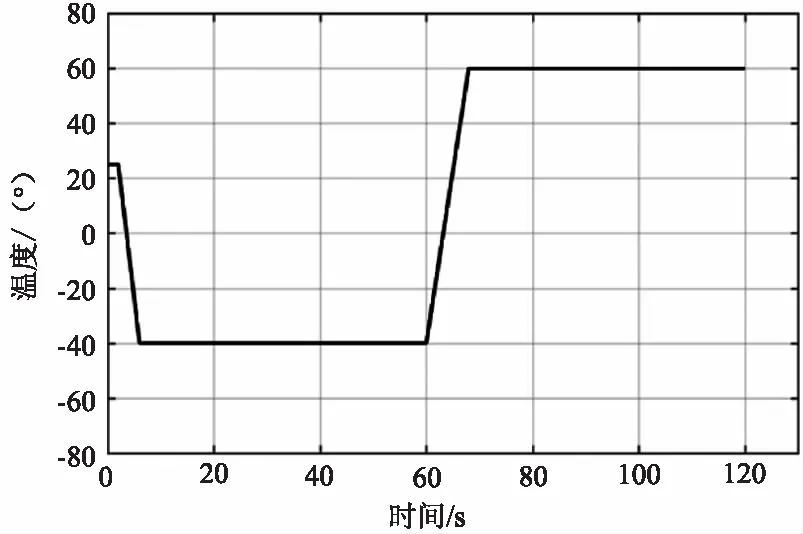
图5 温度激励

3.3 不同加载模式下的SHUP误差

研究过程中分别对FOC模型进行了轴向对称加载、轴向单侧加载、纵向单侧加载和复合加载等不同模式下的热力学仿真。然后利用MATLAB软件对各种加载情况下对称四级和边缘非对称四级结构FOC的SHUP误差进行了定量分析。

(1)轴向对称加载

轴向对称加载方式为光纤环骨架两侧壁同时加载温度激励。该模式下仿真结果如图6所示。图6(a)为FOC每层每匝光纤温度随时间的分布,两种结构的FOC几何空间位置相同的光纤匝(例如第x层第j匝)的温度变化是完全相同的。但是不同结构下该匝光纤在整段光纤上距离光纤起点距离不同,故两种结构下温度梯度沿整根光纤的分布不同,如图6(b)和6(c)所示。根据公式(1),利用图6(b)和图6(c)中的位置、温度梯度等相关参数计算获得的两种结构的SHUP误差结果如图6(d)所示。图7～10的说明与图6类似,后面不再赘述。

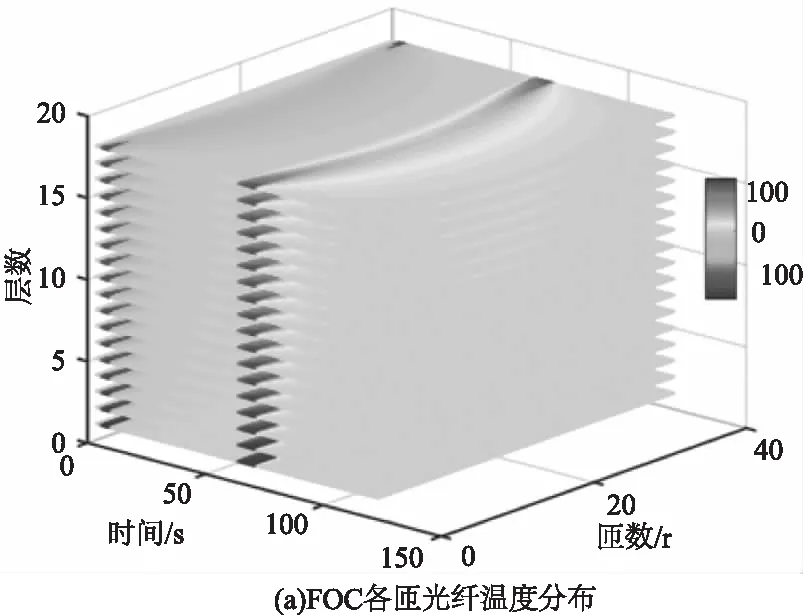
图6 轴向对称温度加载仿真结果

(2)轴向单侧加载

该模式下温度激励从光纤环左侧进行从左到右的轴向加载,仿真结果如图7所示。

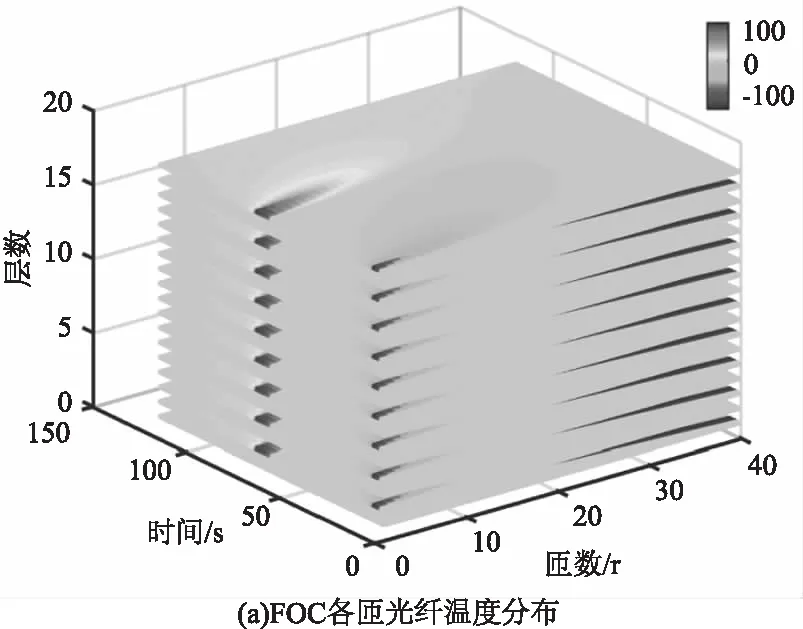
图7 轴向单左侧加载温度加载仿真结果

(3)空气接触面纵向加载

该模式下温度激励从光纤环空气接触面进行由上到下的纵向加载,仿真结果如图8所示。

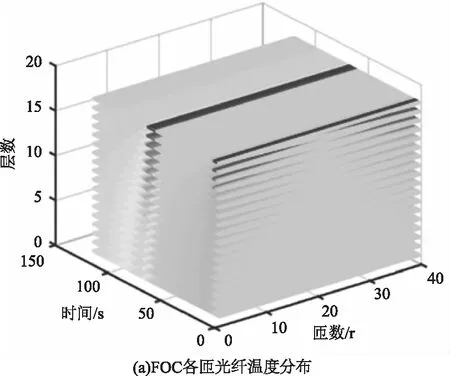
图8 空气接触面纵向加载温度加载仿真结果

(4)骨架接触面纵向加载

该模式下温度激励从光纤环底侧骨架接触面进行从下到上的纵向加载,仿真结果如图9所示。

图9 骨架接触面纵向加载加载仿真结果

(5)复合加载

复合加载方式为光纤环骨架两侧壁和上下表面同时加载温度激励。该模式下仿真结果如图10所示。

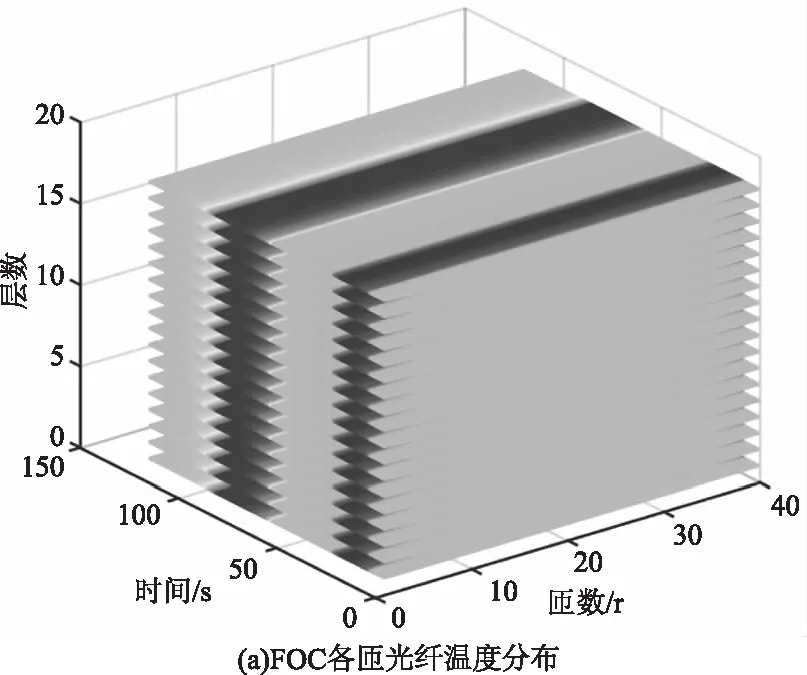
图10 空气接触面纵向加载温度加载仿真结果

通过上述多种不同温度加载模式下的仿真分析结果可知,轴向单侧加载情况下,边缘非对称四级结构的SHUP误差明显大于对称四级结构,这是由于边缘非对称四级结构左右边缘互易性较差,无法有效抑制轴向非对称温度扰动,但是可以通过外部隔热腔体为FOC提供对称的温度环境[9],提高其鲁棒性。其他加载模式下,边缘非对称四级结构的SHUP误差略大于对称四级结构。但是考虑到对称四级结构中光纤换层引起的应力扭曲和剥丝问题,这些误差可以忽略。故本文基于边缘非对称四级结构研究了FOC绕制过程中的自动边缘控制补偿方法。

4 自动边缘控制方法

在原对称四级光纤环绕制系统[10]的基础上,开发了边缘非对称四级FOC绕制技术。从第i=1层开始实现如下步骤的绕纤过程:

(1)右段光纤丝顺时针方向从左到右进行第一层缠绕,绕至FOC骨架右侧壁结束,共缠绕N匝；

(2)右段光纤在FOC骨架右侧壁进行第二层边缘补偿,补偿匝数为1匝；

(3)左段光纤丝逆时针方向从左到右进行第二层缠绕,绕制(N-1)匝结束；

(4)右段光纤在FOC骨架右侧壁进行第三层边缘补偿,匝数为1匝；

(5)左段光纤丝逆时针方向从右到左进行第三层缠绕,绕制(N-1)匝结束；

(6)左段光纤在FOC骨架左侧壁进行第四层边缘补偿,匝数为1匝；

(7)右段光纤丝顺时针方向从右到左进行第四层缠绕,缠绕(N-1)匝结束；

(8)左段光纤在FOC骨架左侧壁进行第五层边缘补偿,匝数为1匝；

(9)右段光纤丝顺时针方向从左到右进行第五层缠绕,绕至FOC骨架右侧壁结束,共缠绕N-1匝；

(10)右段光纤在FOC骨架右侧壁进行第六层边缘补偿,匝数为1匝；

(11)左段光纤丝逆时针方向从左到右进行第六层缠绕,绕制(N-1)匝结束；

(12)右段光纤在FOC骨架右侧壁进行第七层边缘补偿,匝数为1匝；

(13)左段光纤丝逆时针方向从右到左进行第七层缠绕,绕制(N-1)匝结束；

(14)左段光纤在FOC骨架左侧壁进行第八层边缘补偿,匝数为1匝；

(15)右段光纤丝顺时针方向从右到左进行第八层缠绕,缠绕(N-1)匝结束；

(16)重复8～15步,并对缠绕层数进行简单调整,直至所有待绕光纤均匀的缠绕到光纤环骨架上。

上述过程中,步骤切换由自动绕纤程序通过判断当前绕纤匝数、层数、电机运动状态等自动完成。程序流程图如图11所示。

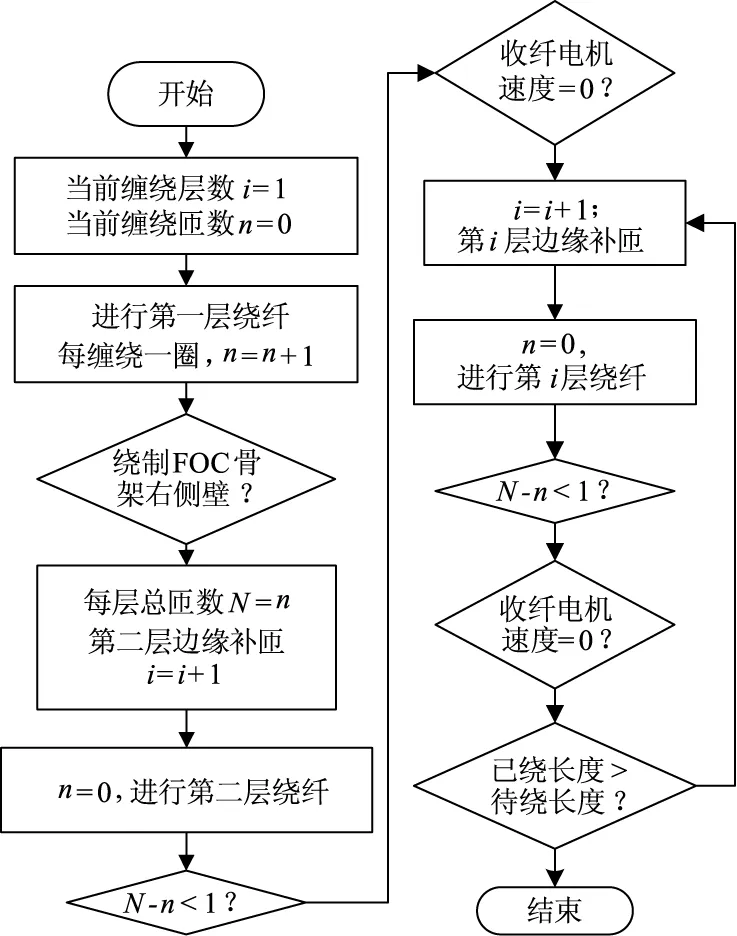
图11 边缘非对称四级光纤环自动绕制流程

利用直径为0.245 mm的裸光纤,在直径为44 mm、长度34 mm的FOC骨架上进行光纤环绕制实验,每层总匝数N=141匝,按照图11所述流程完成了12层光纤环绕制。图12为绕制过程中的FOC实物图。

图12 绕制过程中的光纤环

5 结 论

本文针对FOC对称四级结构中由于跨层换纤引起的应力扭曲、光纤剥丝等绕制缺陷问题,研究了边缘非对称四级FOC自动绕制方法。首先构建FOC三维有限元模型,分析了多种温度加载模式下的边缘非对称四级结构和对称四级结构FOC的热致非互易性误差抑制效果,结果表明,除轴向单侧加载模式下边缘非对称四级结构存在较大的SHUP误差外,其他模式下两种结构之间的SHUP效应偏差较小。然后在原有对称四级绕制系统基础上开发了边缘非对称四级FOC自动绕纤控制技术,可以实现边缘自动判断和光纤匝补偿控制。最后实验表明,利用本文所述方法自动绕制的光纤环结构稳定、排纤均匀。