信号对单模激光损失模型输出特性的影响

叶 庆,李景艳,卿秀华,肖丹琪

(1.武汉纺织大学电子与电气工程学院,湖北 武汉 430074;2.浙江工业大学理学院,浙江 杭州 310023)

1 引 言

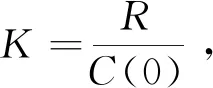
本文考虑了量子噪声实部和虚部之间的关联,运用单模激光损失模型的场幅新方程,用线性化近似方法[6],计算了反映激光动力学性质的光强关联函数[7-8]和平均光强相对涨落C(0)以及信噪比R[9-11],分析了输入信号等系统参数对定义量K的影响,得到了一些新的结果。

2 单模激光方程的计算方法及结果

2.1 线性化近似及关联函数、平均光强相对涨落、信噪比

输入周期信号后的单模激光损失模型的光强方程为:

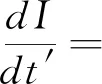
(1)

噪声满足如下统计性质:

(2)

式(1)、(2)中,a0,A为净增益系数和自饱和系数；I,B,Ω分别为光强、输入信号振幅和频率；pR(t′)为泵噪声实部；εr(t′)为相位锁定后的量子噪声；P,Q是泵噪声和量子噪声强度；τ是泵噪声自关联时间；λq为量子噪声实虚部之间的关联系数,其取值范围为-1≤λq≤1。

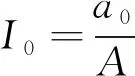
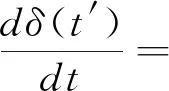
(3)

其中,γ=2a0。

3.2 体位的正确摆放，俯卧位，胸腹部悬空而不直接接触台面，避免对大血管的压迫以减少出血，使胸腹腔容积不减少，使全麻下肺部扩张不受限。

根据稳态平均光强关联函数的定义:

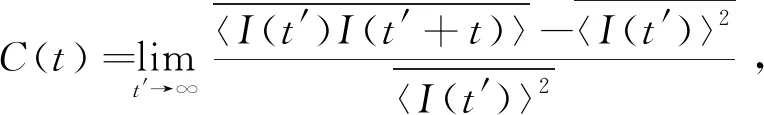
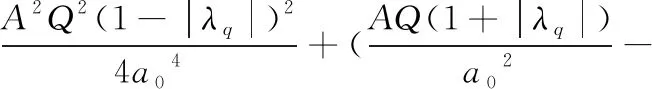
(4)

其中,令t=0,得到稳态平均光强相对涨落:

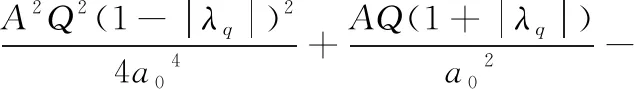
(5)

对式(4)进行傅里叶变换,得输出光强功率谱为:

S(ω)=S1(ω)+S2(ω)

(6)

其中,S1(ω)为输出信号功率谱；S2(ω)为输出噪声功率谱,具体表达式为:

(7)

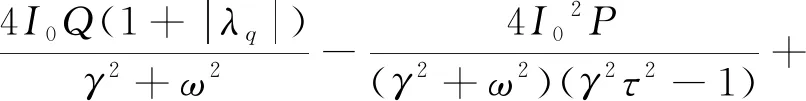
(8)

输出信号总功率[12]为:

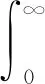
(9)

信噪比定义为输出信号总功率与ω=Ω处的单位噪声谱的平均功率之比(仅取ω>0的谱):

(10)

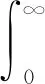
(11)

2.2 单模激光系统的输出信号与稳定性的优化选择

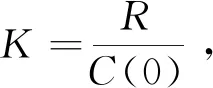
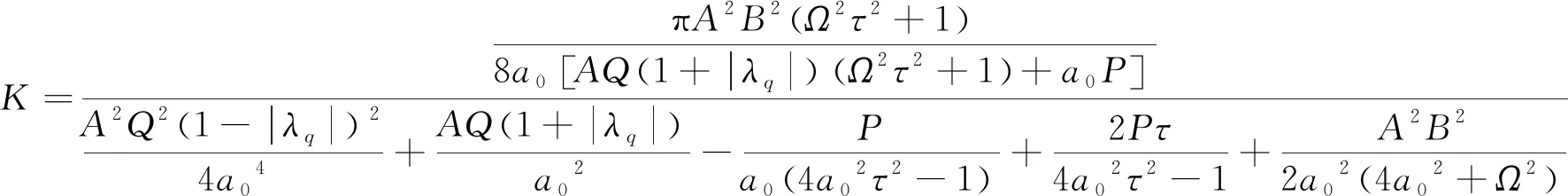
(12)

该量描述了激光系统的优化输出特性,当K取极大值时,系统达到最佳输出信号质量与稳定性的配置。

3 系统稳定性K随净增益系数a0的变化关系

图1(a),图1(b)绘出了信噪比R与系统涨落C(0)之比K随净增益系数a0的变化曲线,发现:在所给定的参数下,K有两个极大值,双峰,即出现双次优化,第一个峰值尖锐,第二个峰值平坦,而且曲线在第一个峰之后随着a0增大迅速单调递减,出现极小值后递增,继而出现第二个极大值后单调递减。由式(12)可知,其中参数的改变对峰值的大小和位置均有影响。

图1(a)是以输入信号振幅B为参数绘出的K-a0曲线,可以看到,曲线出现两个峰值,第一个峰值高于第二个峰值,当输入信号振幅B增大时,曲线峰值增大,随着B等值增大时,峰值等值增大。同时,两个峰值的半高宽几乎没有变化,峰值位置也基本不变。图1(b)是以信号频率Ω为参数绘出的K-a0曲线,从图中看出,第一个峰值略小于第二个峰值,随着Ω的减小,曲线峰值降低,同时,随着Ω等值减小,峰值也等值减小；两峰值半高宽几乎没有变化,峰值位置也几乎不变。图2(a)中,当Ω持续减小,即12.00≤Ω≤12.50时,曲线第一个峰值降低很快,第二个峰值等值减小,直至Ω=10.00时,曲线几乎呈现单峰现象,如图2(b)所示。

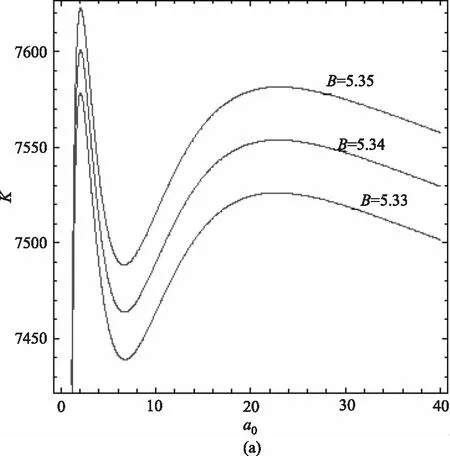
图1 B、Ω为参数时K随a0变化的函数关系图(A=1,P=0.1,Q=0.005,τ=0.2,λq=0.5)

图2 Ω为参数时K随a0变化的函数关系图(A=1,P=0.1,Q=0.005,τ=0.2,λq=0.5)

4 系统稳定性K随自饱和系数A的变化关系

图3(a),图3(b)绘出了信噪比R与系统涨落C(0)之比K随自饱和系数A的变化曲线,发现:在所给定的参数下,K只有一个极大值,单峰,而且曲线在单峰之后随着A增大单调递减,在参数B的图形中,曲线随A的增加会趋于相同的K值,但在参数为Ω的图形中,曲线随A的增大K却有不同的大小。

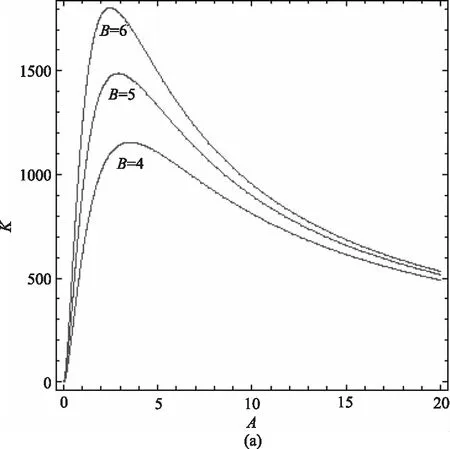
图3 B、Ω为参数时K随A变化的函数关系图(a0=2,P=0.1,Q=0.05,τ=0.1,λq=0.1)

图3(a)是以输入信号振幅B为参数绘出的K-A曲线,可以看到,当输入信号振幅B增大时,曲线峰值增大,随着B等值增大时,峰值近似等值增大。同时,峰的半高宽度略有减小,峰值位置略有左移。图3(b)是以输入信号频率Ω为参数绘出的K-A曲线,从图中看出,随着Ω的增大,曲线峰值升高,随着信号频率等值增大时,峰值也是等值增大,峰值的半高宽几乎不变,峰值位置略右移。

5 系统稳定性K随泵噪声自关联时间τ的变化关系

以B为参数,信噪比R与系统涨落C(0)之比K随泵噪声自关联时间τ的变化曲线如图4(a),4(b)所示,发现:在所给定的参数下,曲线随泵噪声自关联时间的增大呈单调递增的趋势,当 2≤B≤5,K值递增较快,当5≤B≤8时,K值递增缓慢,明显可以看出随着B等值增大时,K值增大速度越来越缓。正如图4(b)所示,当8≤B≤15时,很明显可以看出,当K值几乎等值增大时,B值却不是等值增大的。

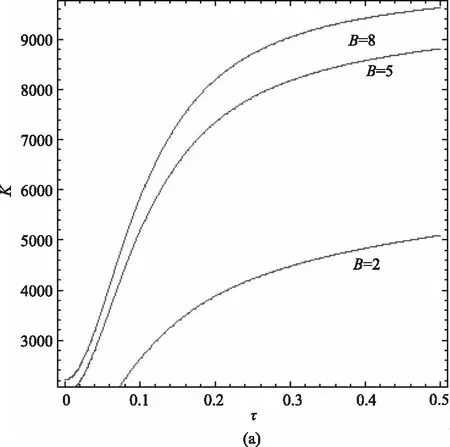
图4 B为参数时K随τ变化的函数关系图(a0=1,A=4,P=0.1,Q=0.005,λq=0.5)

图5(a)、(b)绘出了以输入信号频率Ω为参数绘出的K-τ曲线,从图中看出,在输入信号频率8≤Ω≤10中,当Ω稍大时,曲线呈现的是上凸式单调递增的趋势；当频率较低时,如0.9≤Ω≤1.1时,曲线呈现的是下凹式单调递增的趋势；同时Ω增大,曲线K值增大。

图5 Ω为参数时K随τ变化的函数关系图(a0=1,A=4,P=0.1,Q=0.005,λq=0.5)

6 结 论

综上所述,K随激光系统的净增益系数a0存在未研究发现的双极大值；与自饱和系数A之间存在单极大值,极大值即是系统最佳匹配状态,发现,极大值的半高宽越窄,峰值越尖锐,说明优化性能更好；与泵噪声自关联时间τ不存在极大值,但是随参数的变化有不同程度的影响；曲线峰值均会随输入信号振幅B、输入信号频率Ω的增大而增大；同时,K-τ曲线中K值也是随着信号振幅B和频率Ω的增大而增大,也就是说,输入信号振幅、频率的增大均能优化激光通讯系统输出性能。