基于双树复小波变换的红外小目标检测算法

王 鹤,辛云宏

(陕西师范大学物理学与信息技术学院,陕西 西安 710119)

1 引 言

红外成像技术通过几十年的发展,被广泛应用于各个领域。但由于目标受长距离,复杂背景,太阳辐射和不确定噪声等因素的影响,导致红外图像信噪比低,且红外小目标没有特定的形状和纹理,边缘模糊,因此红外小目标检测仍然是一个需要继续研究的课题。

一般来说提高红外小目标的检测能力,需要对背景噪声和杂波进行抑制,同时增强红外小目标的信噪比。目前有许多经典的基于图像滤波的红外小目标检测算法,如最大均值(Max-mean)和最大中值(Max-median)滤波[1-2],二维最小均方(Two Dimensional Least Mean Square,TDLMS)滤波[3-4],双边滤波[5-6]和形态学滤波[7]等。经典的滤波算法计算量少,复杂度低,但在复杂背景下,其检测结果准确率低。其次还有基于变换域滤波的检测算法,其通过相应的变换,将图像的高低频分离,分别对高低频进行滤波处理,从而实现小目标的检测。基于变换域的滤波算法有基于小波变换的滤波检测[8-10],基于曲波变换的背景抑制检测[11-12],基于Contourlet变换的检测[13-14],基于Shearlet变换的检测[15-16]等。基于变换域的滤波算法相较于传统滤波,在可靠性上有所提升。近几年一些基于图像数据结构的算法被提出。如利用小目标和周围背景信息不连续的特点,做局部对比,来增强小目标并提高图像的信噪比。如基于局部对比度测量(LCM)[17]和基于多尺度灰度差分的检测算法[18]。该类算法在杂波和噪声严重时,检测效果一般。后来有人提出基于低秩红外模型(Infrared Patch Image,IPI)[19-20],将图像进行低秩稀疏分解,来实现小目标的检测。该类方法不仅能适应低信噪比图像的检测,且对于较为复杂的背景同样有很高的复杂度。但是以计算量作为代价,时间复杂度高,很难满足实时性的需求。

综上所述,变换域方法是一类有效的目标检测方法,但是经典的小波变换方法缺乏方向性,且不具备平移不变特性,其检测性能往往不能满足实际应用需求。近年来,双树复小波分析作为一种有效的图像处理方法,被许多学者应用于目标检测领域[23-25],但是将其直接应用于红外小目标检测时,由于其对图像中的高频信息特别敏感,无法在保留目标的同时有效地滤除噪声[26]。本文提出了一种基于双树复小波变换与图像熵的红外小目标检测算法,能够有效去除图像中的杂波,同时凸显出小目标。

2 红外小目标检测算法

本文所提出的算法包含背景抑制和小目标增强两个步骤。其中,背景抑制部分是通过对图像进行双树复小波分解后处理系数实现,小目标增强部分是通过图像熵加权实现。算法的详细流程如图1所示。

图1 本文算法流程

2.1 双树复小波变换

传统的二维离散小波变换缺乏平移不变性,只提供水平,垂直,对角三个方向的高频子带,缺乏方向选择性。为了解决传统小波变换存在的问题,1998年剑桥大学的kingsbury等人提出了双树复小波变换(DT-CWT),双树复小波变换的提出克服了传统小波变换的缺点,它继承了小波变换的时频特性,还具备了平移不变性和6个方向的信息,能够反映出图像在多尺度下不同方向的变化。

复数小波可表示为:

ψ(t)=ψh(t)+jψg(t)

(1)

式中,ψh(t)和ψg(t)分别表示复数小波的实部和虚部部分,并且它们都是实函数。

图2中给出了双树复小波变换的滤波器组,树A和树B分别表示双树复小波变换的实数部分和虚数部分。

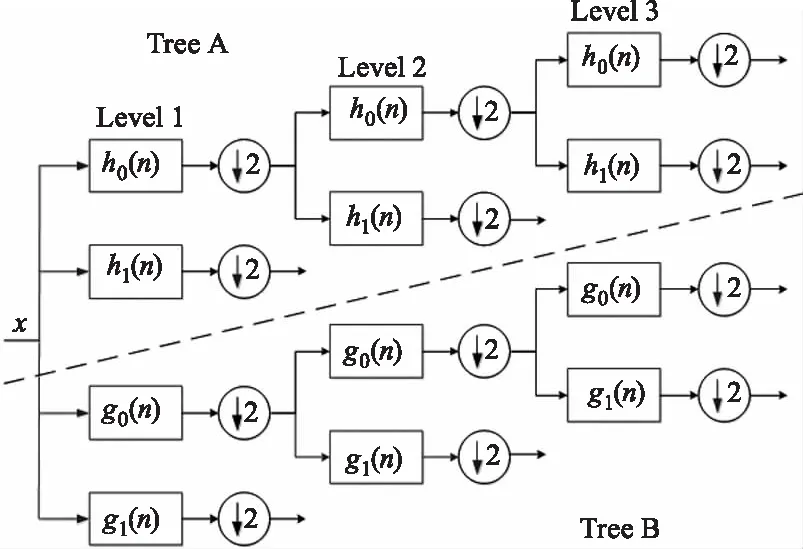
图2 一维DT-CWT分解图

类似于二维离散小波变换,二维双树复小波变换是可分离实现的变换,先是对图像的每一行进行一维的双树复小波变换,再对图像的每一列进行一维的双树复小波变换。这样在第1,2象限分别产生3个子带,对应空间的六个方向:±15°,±45°,±75°。因此,双树复小波变换有更多的方向选择,可以提高和增强某个方向上的边缘和纹理特征信息。实验表明采用双树复小波做变换域,可以将图像分解在更多的方向上,有效去除背景噪声。

2.2 改进Top-Hat

对低频子带采用改进的Top-Hat形态学滤波,改进的Top-Hat形态学是在灰度形态学的基础上改进的。

改进的Top-Hat开运算表示为f|Soi,定义为:

f|Soi(x,y)=(f⊕ΔSb)⊖Sb

(2)

闭运算表示为f|Soi,定义为:

f|Soi(x,y)=(f|ΔSb)⊕Sb

(3)

白帽和黑帽运算可定义为:

NWTH(x,y)=f(x,y)-f|Soi(x,y)

(4)

NBTH(x,y)=f|Soi(x,y)-f(x,y)

(5)

从上可以看出改进的Top-Hat变换与经典的Top-Hat运算顺序是相反的。在本文选取的是外径为5,内径为2的圆盘作为结构元素。

2.3 局部图像熵

信息熵表示一个信息源中有多少信息,它可以均匀地表示一个信息源的全局特征。类似地,图像熵是基于图像的直方图构造的,它可以有效地表明图像上灰度值分布的复杂程度。对于图像I,其大小为M×N且有L个灰度级,其图像熵的定义为:

(6)

其中,pi是第i个灰度级的概率密度函数;ni为第i个灰度级的像素数。

图像的信息熵具有统计显著性,但它忽略了图像的纹理和频率信息。因此,本文用局部熵算子,使其被限制在一个大小为Mk×Nk的局部窗口中,它可以表示窗口中包含的信息内容。当红外图像中出现一个小目标时,目标周围局部区域的纹理特征被破坏,产生局部熵的变化。根据最大熵原理,灰度值变化平缓区域的熵值大于变化剧烈区域的熵值。局部熵算子在一定程度上可以用来增强复杂背景下的红外小目标。计算局部图像熵算子的方法如下:

局部熵算子1)给出每个像素点的邻域大小2)for x=1:M do3)for y=1:N dopij=Ii,j /∑x+(m-1)/2s=x-(m-1)/2∑y+(n-1)/2t=y-(n-1)/2Is,t ,i=x-(m-1)/2:x+(m-1)/2,j=y-(n-1)/2:y+(n-1)/24)E4x,y =-∑x+(m-1)/2i=x-(m-1)/2 ∑y+(n-1)/2j=y-(n-1)/2pijlog2pij5)用E4x,y 代替中心像素的值6)end for7)end for

其中,I(x,y)为中心像素值；m,n为局部窗口大小。

本文采用7×7大小的图像块计算局部图像熵,将采用上述算法得出的图像熵矩阵与经过二次双树复小波重构的图像做点乘,以实现对重构图像中小目标的增强。

2.4 算法实现步骤

基于双树复小波变换和图像熵的红外小目标检测算法的具体实现步骤如下:

将流量调至62m3/h（标准状态下），考查不同功率对臭氧浓度、产量、转化率及经济性的影响，每个工况间隔时间为2h，以保证系统处于稳定状态，并采取3个出气平行样进行分析。

1)将图片进行双树复小波分解,通过将低频子带置零的方法将图像的大面积背景进行滤除,再将高频子带进行融合。

2)对融合后的图片再进行双树复小波分解。

3)低频子带进行改进的Top-Hat滤波,再与原低频子带进行差分。

4)将±45°和±75°方向的高频子带置零,±15°向的高频子带用高通滤波器滤波。

5)将差分处理后的低频子带与滤波处理后的高频子带进行融合。

6)用计算局部熵算子的方法计算出局部图像熵矩阵。

3 实验结果及分析

本实验采用天空背景,建筑物背景以及含有大量杂波干扰等的6个大小为384×288的红外目标图像进行仿真实验,分别用Top-Hat,鲁棒性主成分分析(Robust Principal Analysis,RPCA),频谱尺度空间(Spectrum Scale Space,SSS),小波变换算法,只做一次双树复小波分解的算法(算法1)和没有经过图像熵加权的算法(算法2),总共六组作对比实验。仿真结果如图3所示。其中,(a1)～(a6),(b1)～(b6),(c1)～(c6),(d1)～(d6),(e1)～(e6),(f1)～(f6),(g1)～(g6),(h1)～(h6)分别为原始图片以及对应的三维图,Top-Hat算法处理结果和对应的三维图,RPCA算法处理结果和对应的三维图,SSS算法处理结果和对应的三维图,小波变换处理结果和对应的三维图,算法1处理结果和对应的三维图,算法2处理结果和对应的三维图,本文算法处理结果和对应的三维图。

(a1) (b1) (c1) (d1) (e1) (f1) (g1) (h1)

(a2) (b2) (c2) (d2) (e2) (f2) (g2) (h2)

(a3) (b3) (c3) (d3) (e3) (f3) (g3) (h3)

(a4) (b4) (c4) (d4) (e4) (f4) (g4) (h4)

(a5) (b5) (c5) (d5) (e5) (f5) (g5) (h5)

(a6) (b6) (c6) (d6) (e6) (f6) (g6) (h6)

图3 不同方法检测结果的二维和三维对比图

对比这六组检测算法的结果图像可以看出,当红外图像清晰,且背景结构简单时,这七组算法均可以检测出小目标,但算法2和本文算法相比较于其他算法,背景抑制效果最好。当背景中出现大片的云时,Top-Hat、RPCA、小波变换以及算法1不能很好的滤除云层。当小目标隐藏在云层中时,SSS、小波变换、算法2和本文算法能够很好地抑制背景,凸显小目标。

为了进一步表面本文算法的优越性,实验引入两种常见的评价指标:信号杂波比(SCRG)和背景抑制因子(BSF)。SCRG和BSF的定义如下:

(7)

其中,MT,MB分别表示图像中小目标和图像背景的灰度均值,DB表示图像背景的标准差；(·)in表示输入图像的参数；(·)out表示输出图像的参数。

六种类型图像的实验数据如表1和表2所示。根据式(7)的定义可知,当处理同一幅图像时,Din是相同的,而Dout由处理后的图像中残余背景的灰度值计算得到。当残余背景越少时,整幅图像的背景标准差Dout就越小,即背景抑制效果越好,得到的BSF的值也就越大,同理,SCRGout表示的处理后图像的信杂比,值越大说明背景效果抑制越好,小目标和背景的灰度差值也就越大,得到的SCRG的值也就越大。从表1中可以看出,本文算法的BSF值和SCRG值相较Top-Hat,RPCA,SSS,小波变换,算法1和算法2是里最大的,表明本文算法很好的抑制了背景,比较算法2和本文算法,从结果图上看两者基本一样,但从评价指标来看,本文算法的BSF值和SCRG值均高于算法2,说明本文算法提高了小目标和背景的信杂比,增强小目标。

表1 不同方法的BSF指标数据

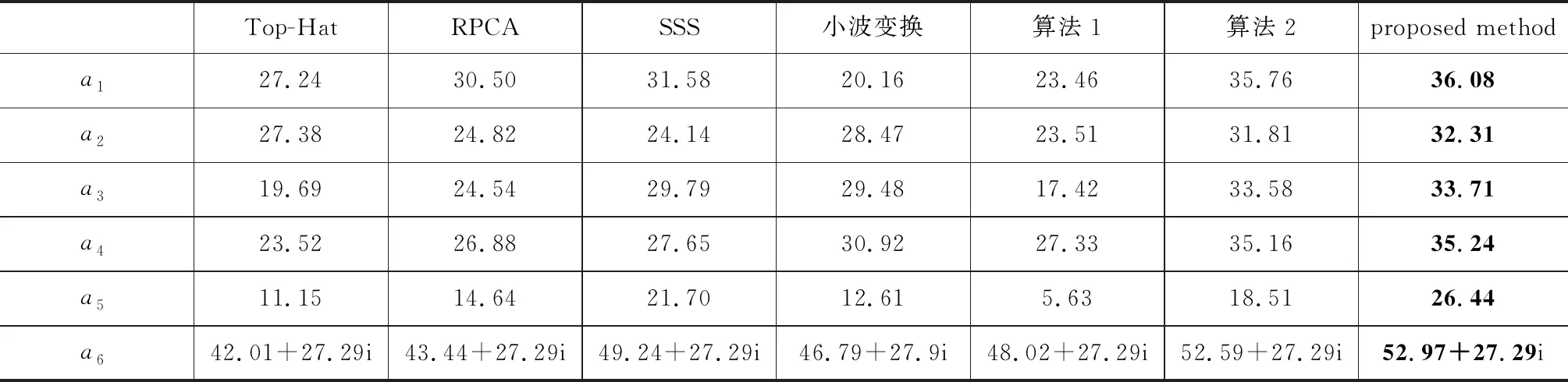
表2 不同方法的SCRG指标数据

同时,实验还增加接受者操作特性(Receiver Operating Characteristic,ROC)曲线作为评价指标,ROC曲线描述的是检测率(Probability of detection,Pd)和误警率(False alarm rate,Fa)之间的关系。Pd和Fa的定义如下:

(8)

(9)

其中,nt为检测到的小目标的像素数;nc为小目标的实际像素数;nf为误检的小目标像素数;n为图像的总像素数。ROC曲线下的面积(Area Under ROC Curve,AUC)决定了ROC曲线的质量,一个好的检测算法,在相同的Fa情况下,其Pd的值更高,即AUC的面积更大。五种图像的检测算法的ROC曲线如图4所示,从图中可以看出,本文算法相较于其他算法,AUC的面积最大,说明本文算法在相同的误警率下,具有更高的检测率,总体来说,本文算法是这几个对比算法中最好的算法。

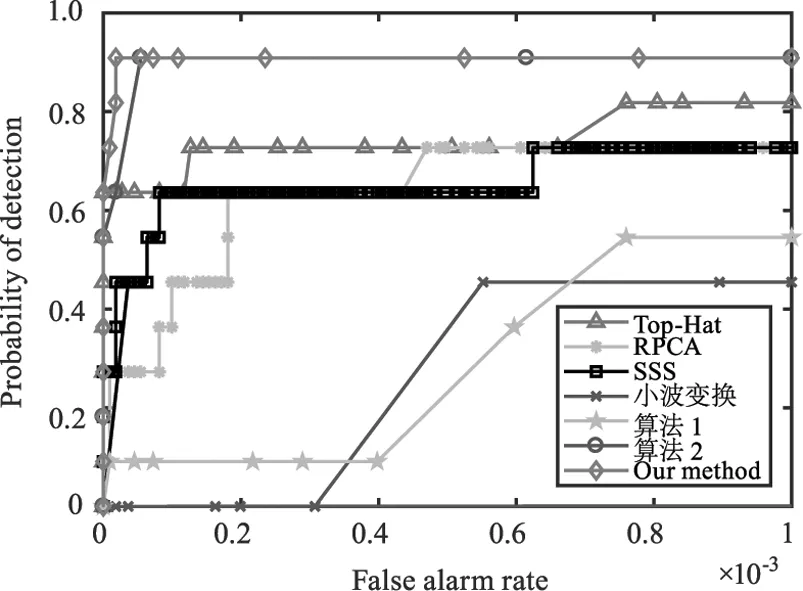
(a) ROC curve contrast diagram of image a1

4 结 语

本文提出了一种基于双树复小波和图像熵的红外小目标检测算法,并通过对比实验对算法性能进行了验证。实验结果表明,所提出方法可以有效的去除背景图像中的杂波,凸显小目标,实现小目标的可靠检测；在BSF值、SCRG值以及ROC曲线等客观评价指标方面具有明显优势。因此,本文提出的算法是一种有效红外小目标检测算法,该方法还可应用于其他相关领域。