基于单MZM和FBG的10倍频抑制载波RoF系统

王现彬,杨彦彬,卢智嘉,高彦彦

(石家庄学院机电学院,河北 石家庄 050000)

1 引 言

由于频谱资源稀缺,未来高速通信将主要依赖毫米波频段,但受电子瓶颈影响电域产生毫米波信号难度较大,在光域中实现毫米波传输具有较强吸引力。基于此的光载无线通信技术(RoF)集光纤通信和无线通信于一体,以低成本、大容量、高保密性、易于多业务融合等特征,成为未来超高速无线通信“最后一公里”接入的首选解决方案[1-7]。对于光载毫米波,相关研究者提出了诸如直接调制、光外差、四波混频及外部调制等不同的生成技术[8-11],其中基于外部调制的光生毫米波技术方案实现简单、稳定性高且产生的光载毫米波信号噪声低,受到了广泛关注。相关技术报道中外部调制方式一般也都是采用两级马赫曾德尔外调制器(MZM),并附加一些滤波器或特殊光器件,导致系统结构复杂且插入损耗较高,增加了中心站(CS)建设成本,同时进一步降低了系统性能[12-14]。为此提出了一种基于单MZM和FBG的10倍频抑制载波RoF产生结构,对基于该结构的10倍频抑制载波光载毫米波产生进行了理论分析,优化了FBG带宽及反射率,并通过实验验证了理论的正确性,为实际RoF系统设计提供了参考思路。

2 原理分析

所提出的基于单MZM和FBG的10倍频抑制载波RoF系统下行链路如图1所示。在CS站通过设置MZM直流偏置电压和射频驱动信号幅度,由一个MZM实现基带信号调制与偶数阶边带抑制(包括主载波),再借助光纤布拉格光栅(FBG)滤除多余奇数阶边带。通过标准单模光纤信道传输后,在基站(BS)通过PIN光电二极管拍频产生电毫米波信号,借助BS站端的射频天线将电毫米波信号传输到移动终端(图1中省去了射频天线,直接采用混频器(Mixer)解调出基带信号)。CS站由光源(LD)、MZM、乘法器、移相器和FBG构成,首先基带信号S(t)和射频驱动信号Er(t)通过相乘器后分成两路,一路控制MZM的射频上端口,一路π相移后控制MZM的射频下端口,MZM的直流电极则一路接地一路接偏压a。

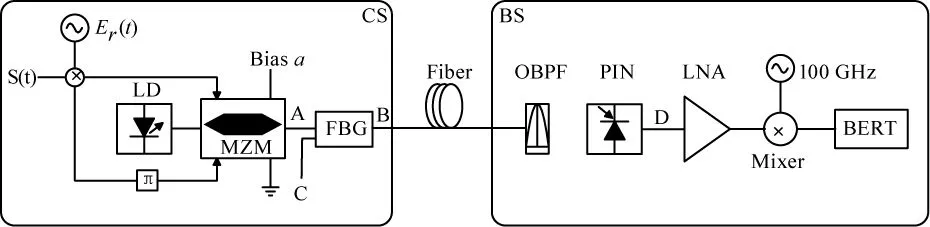
图1 基于单MZM和FBG的10倍频抑制载波RoF系统框图

假设激光器发出的连续光波为Ein(t)=A0·exp(jω0t),其中A0和ω0为光信号的幅度和角频率。待传数据S(t)=∑Img(t-mT),其中Im为伪随机二进制数据串,g(t)为伪随机二进制数据波形(本文采用矩形波),T为一个码元的宽度。射频驱动信Er(t)=Arcos(ωrt),其中Ar和ωr为射频驱动信号的幅度和角频率。射频驱动信号Er(t)和待传数据S(t)通过相乘器后分别控制MZM的两射频电极,且两路信号反相,即上臂为v1(t)=S(t)Er(t),下臂为v2(t)=-S(t)Er(t)=-v1(t)。此时MZM的输出光场为:

(1)

其中,IL为插入损耗,在理论分析时假定IL=0;γ为上下两臂的分光比,一般取γ=0.5;Vbias1和Vbias2为上下臂的直流偏置电压,令Vbias1=0 V,Vbias2=4 V(即偏压a);VπDC为直流半波电压,VπRF为射频半波电压,且VπDC=VπRF=4 V;利用贝塞尔函数将式(1)展开为:

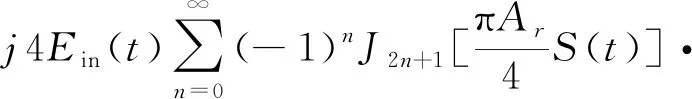
cos[(2n+1)ωrt]

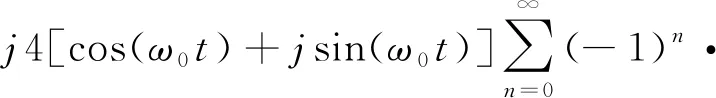
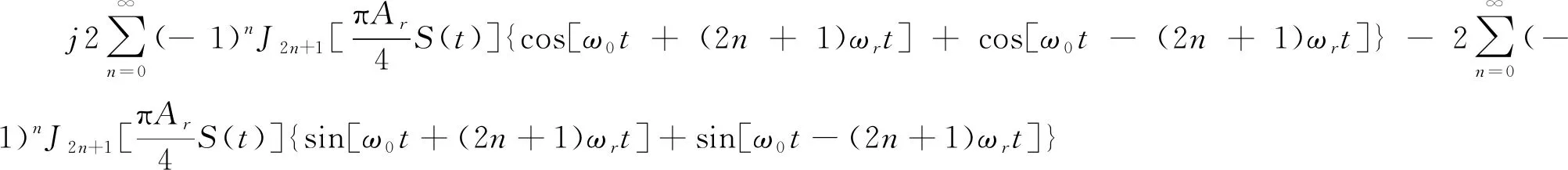
(2)

式中,J2n+1为(2n+1)阶第一类贝塞尔函数。在式(2)中,令β=πArS(t)/4,称为调制深度。从式(2)可以看出,MZM输出的已调光信号中心载波和偶数阶边带得到了抑制,只存在奇数阶边带。

图2为奇数阶的第一类贝塞尔函数曲线,从图2可以看出,当β为3.821时,1阶和7阶贝塞尔函数为0。为此设置射频驱动信号幅度为4.868,结合VπDC=VπRF=4 V,可使产生的光载毫米波只保留3阶和5阶边带,更高阶的Jn(β)由于幅度太小可以忽略不计。则式(2)变为:

图2 第一类贝塞尔函数

Eo(t)=j2J3(β)[cos(ω0t+3ωrt)+cos(ω0t-3ωrt)]-2J3(β)[sin(ω0t+3ωrt)+sin(ω0t-3ωrt)]+j2J5(β)[cos(ω0t+5ωrt)+cos(ω0t-5ωrt)]-2J5(β)[sin(ω0t+5ωrt)+sin(ω0t-5ωrt)]

(3)

随后将该信号通过FBG滤除3阶边带,最后只留下5阶边带。再将只含有5阶边带的Eo(t)在BS站经PIN光电二极管平方律检波后,若不考虑PIN光电二极管响应噪声,则输出电流为:

(4)

3 实验研究

系统框图如图1所示,系统参数除前述相关参数外,基带信号速率设定为2.5 Gbit/s,传输(231-1)个伪随机二进制数据。LD光源的中心光频率为193.1 THz,线宽为10 MHz,输出功率为0 dBm。射频驱动信号Er(t)幅度为4.868 V,频率为10 GHz。FBG中心频率为193.1 THz,与光源中心频率一致。标准单模光纤衰减系数为0.2 dB/km,色散系数为16.75 ps/(nm·km),差分群时延为0.2 ps/km,有效纤芯面积为80 μm2。贝塞尔光带通滤波器中心频率设定为193.1 THz,带宽为0.3 nm。PIN光电二极管响应度为1 A/W,暗电流为10 nA。

图3给出了图1中A、B、C和D处的频谱图。从图3(a)可以看出,经过单MZM调制后,实现了载波及各偶阶边带的抑制,只留下3阶和5阶奇数阶边带,而更高阶的奇数阶边带由于其值过小显示不出来,与理论分析完全吻合。图3(b)为经过FBG滤波后所留下的5阶边带,可以看出其边带抑制比约为18 dB,3阶边带对5阶边带的影响得到了有效降低。图3(c)为FBG滤出的3阶边带,该光信号经偏振复用到达基站并解复用后可作为上行链路载波信号。图3(d)为背靠背传输时(Back to back)接收端经PIN光电二极管后所对应的射频频谱,在10倍于射频驱动信号Er(t)频率,即100 GHz处存在一个有效频谱,实现了射频驱动信号的10倍频传输。可以看出该射频频谱峰值功率较低,后续可以采用放大器将其放大以实现远距离传输。由于主载波并非完全抑制,从而在20 GHz处存在一个毫米波信号,但与100 GHz处的主毫米波信号相比功率相差15.49 dB,再结合后续射频天线和混频器的带宽有限性,其影响可以忽略。

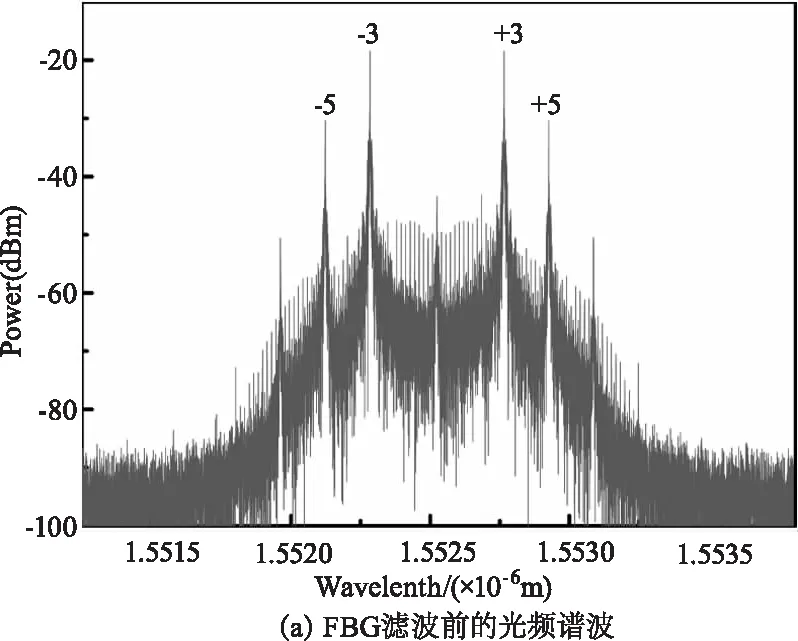
图3 RoF系统中A、B、C和D处频谱图

图4为不同反射率时FBG带宽与误码率对应关系。从图可以看出随着FBG带宽的增大,误码率先降低后增大,呈现出U形分布状态,当反射率为0.9时其变化趋势仍满足U形分布,只是变化趋势较为缓慢。误码率呈现出的这种变化可以解释如下:当FBG带宽较窄时,无法完全滤除3阶边带,残留的3阶边带在PIN光电二极管拍频时产生不利影响,造成误码率较高,随着3阶边带滤除量的增大,误码率逐渐降低,当3阶边带完全滤除时误码率达到最低。随着FBG带宽继续增大,除了3阶边带被滤除,5阶边带也受到影响,造成有用信息丢失,从而引起误码率升高。从图4可以看出反射率为0.99、0.999和0.9999时的最优系统带宽分别为0.804、0.8和0.798 nm,对应的最低误码率分别为10-14、10-20和10-16数量级,即三种情况下误码率最低值分布在0.795～0.805 nm之间,且随着反射率的增大,最低误码率也是表现为先降低后增大的U形结构。

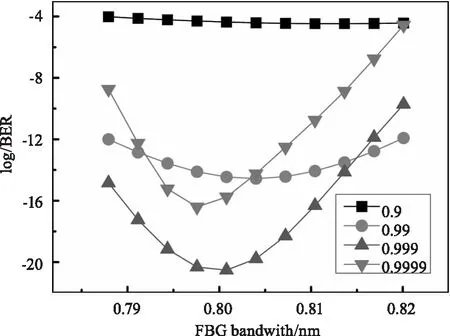
图4 误码率与FBG带宽对应关系

为寻找最优反射率,分析了不同带宽下FBG反射率与误码率的对应关系,如图5所示,而这些不同的带宽都位于0.795～0.805 nm的最优带宽内。从图5可以看出,随着FBG反射率的增大,不同带宽FBG下的系统误码率都呈现出相同的下降趋势,且整体误码率较为接近。从图5插图可以看出,在某一FBG反射率下,FBG带宽从0.7976 nm到0.8032 nm变化时误码率依次略有降低,但下降幅度较小。当FBG反射率为0.9966时,误码率达到最低,此后系统性能极速变差。实际FBG制作时反射率越大越难实现,故FBG反射率选择应折中考虑。

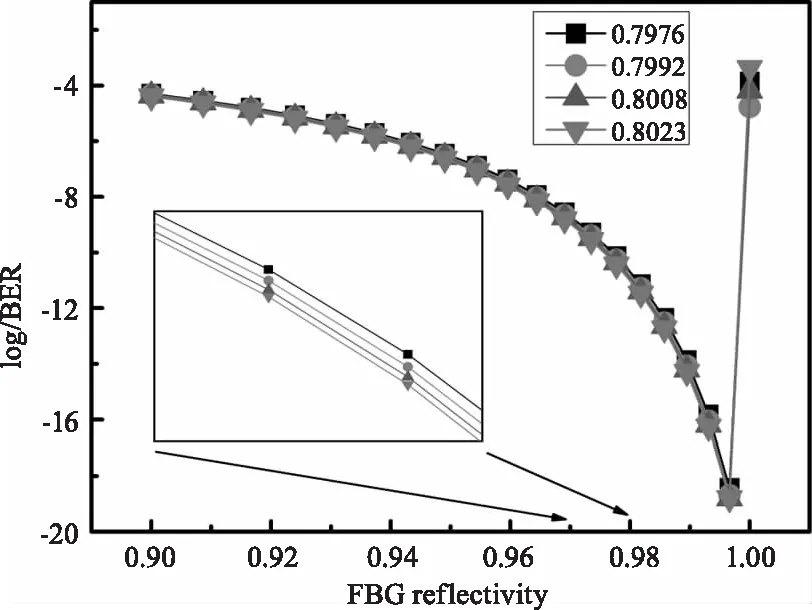
图5 FBG反射率与误码率对应关系

在上述FBG优化参数下,分析了基于单MZM和FBG的10倍频载波抑制ROF系统背靠背和传输20 km时接收端光功率与误码率的对应关系曲线,如图6所示,其中的插图为两个点测量时对应的眼图。当误码率为10-9时,背靠背的接收端光功率为-43.26 dBm,而传输20 km后的接收端光功率为-41.6 dBm,功率代价为1.66 dB,表现出了较好的系统性能。

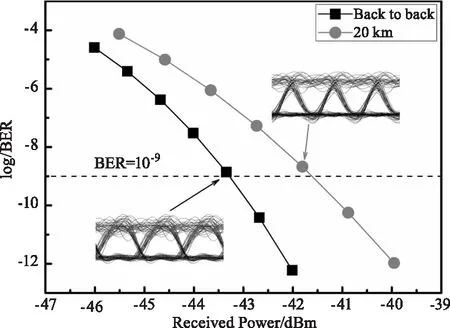
图6 接收功率与误码率对应关系

4 结 论

提出了一种基于单MZM和FBG的10倍频抑制载波毫米波产生结构,通过设置射频驱动信号幅度及MZM偏置电压,产生载波及偶数阶边带抑制的RoF信号。当射频驱动信号幅度为4.868 V、MZM偏置电压为4 V时,RoF信号中主要包含3阶和5阶边带,更高阶的奇数阶边带由于其幅值过低忽略不计。随后利用FBG的滤波特性滤除3阶边带,只保留5阶边带,到达接收端后通过PIN光电二极管拍频后产生10倍频毫米波信号。结果表明当FBG带宽为0.795～0.805 nm时,可实现较低误码的系统传输；在该带宽范围内,当FBG反射率为0.9966时,系统误码率达到最低。利用FBG参数优化后的新型RoF系统传输20 km后与背靠背系统相比功率代价仅为1.66 dB,表现出了较好的系统性能。