蓉欧+境内集装箱集疏运系统优化及仿真

刘露露，汤银英，陈 思

蓉欧+境内集装箱集疏运系统优化及仿真

刘露露，汤银英，陈 思

（1. 西南交通大学，交通运输与物流学院，成都 611756；2. 综合交通运输智能化国家地方联合工程实验室，成都 611756）

在蓉欧+发展战略下，本文针对中欧班列（成都）发展现状和当前集疏运系统存在的问题，以集疏运成本最小为目标函数，以货物的运输时限等作为约束条件构建模型，通过基于优先级的分段式编码的遗传算法对模型求解，并在不同运输时限下进行仿真实验。结果表明：对于距离成都国际铁路港较近的昆明、贵阳、重庆和距中转地较远的南宁，应高度重视铁路集疏运的方式；对于距离中转地较近的厦门、宁波、日照，应注重与武汉、上海等中转地之间的合作，通过多式联运降低成本；对于距离中转地居中的广州、天津，不仅要注重铁路集疏运方式的发展，同时应注重与武汉、上海等中转地之间的合作。

蓉欧+；运输时限；遗传算法；仿真

0 引 言

在蓉欧+战略背景下，中欧班列（成都）在境内形成了以成都国际铁路港为依托，腹地范围由四川周边地区扩大到全国地区的集疏运系统，通过该集疏运系统，可为中欧班列（成都）集散货物。中欧班列（成都）运价约为海运的2.6倍左右，时间上则仅是海运的40%，但由于成都国际铁路港处于内陆，两端集疏运成本偏高，因此如何在保持运输时效优势的前提下降低集疏运成本是当前值得探讨的一个问题。

国内外对于集疏运的研究主要集中于以下几方面：第一，对于集疏运系统的研究，主要研究集疏运系统的主体、组成及主要构成环节[1-4]。第二，针对港口码头的集疏运研究，有的人从计算机操作系统和虚拟结构以及Agent角度提出集装箱码头物流系统的优化建议[5, 6]，有的学者提出应用离散仿真模型来研究码头通过能力，研究者借助离散仿真平台，构建各个码头物流环节的仿真模块，研究码头通过能力[7, 8]。还有的学者从低碳经济的角度出发建立泊位分配模型并利用遗传算法求解[9]。第三，对于港口与腹地城市的研究，如Chang TS[10]研究了集疏运最优路径的选择问题；Hao C[11]等以成本最小为目标，构建了内陆集疏运系统优化模型；冯震[12]等以时间成本最小为目标，提出了复杂网络目标评价的优化函数，并设计改进算法进行求解；蒋先稳[13]则利用博弈论的知识对港内集装箱码头腹地和转运业务进行竞合研究。

本文将在已有研究基础上针对中欧班列（成都）发展现状以及集疏运系统存在的问题，以集疏运成本最小为目标函数，针对不同运输时限要求进行仿真，提出优化建议，以期降低集疏运成本。

1 问题描述及模型建立

1.1 集疏运系统描述

集疏运系统包括港口、腹地、集疏运方式、中转地，蓉欧+境内集疏运系统和网络如图1和图2所示，其中“集”指通过铁路、公路、水运等多种运输方式将腹地货物运送至成都国际铁路港，并最终通过中欧班列（成都）运送至欧洲各地；“疏”指通过中欧班列（成都）运至成都国际铁路港的货物从铁路港发散至腹地。随着蓉欧+战略的实施，国内逐步建设由成都到上海、广州、武汉、宁波、昆明、厦门、广州、南宁、青岛、天津、日照等沿海沿边城市的集装箱快速互联互通通道，使得昆明、贵阳、重庆、武汉和厦门、上海、广州、南宁、天津、日照、宁波沿海沿边城市成为成都国际铁路港的腹地[14]，编号为1~11。此外，由于成都国际铁路港处于我国内陆，货物的集运除了通过陆路运输外，还可通过泸州、武汉、上海以水运形式展开，因此将泸州港、武汉和上海作为中转地，编号为12~14。同时，成都国际铁路港作为集疏运系统的港口编号为15。

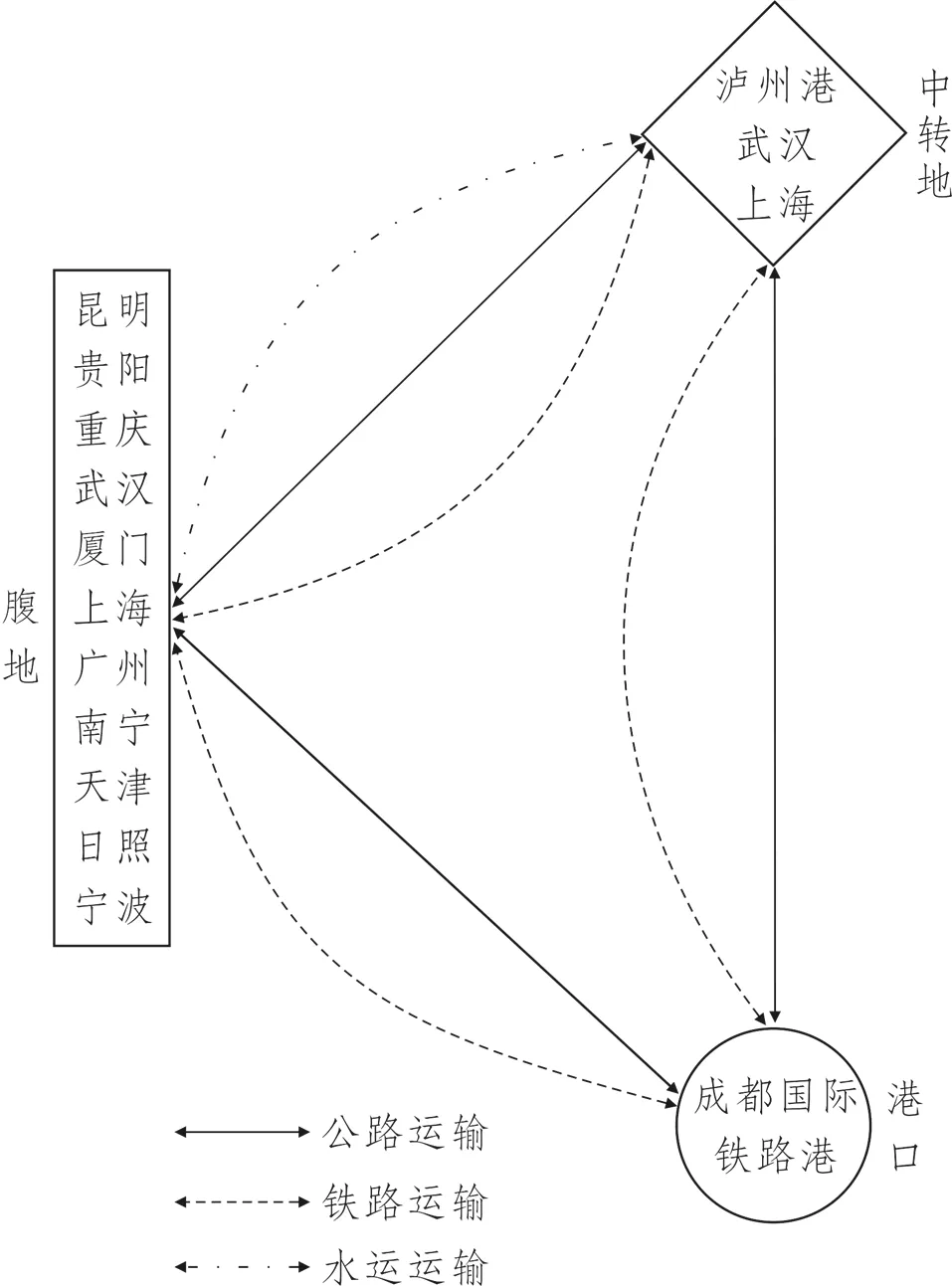
图1 蓉欧+境内集疏运系统

图 2 蓉欧+境内集疏运网络

1.2 模型建立

1.2.1 模型假设

模型假设如下：

（1）每个腹地在同一时间发出的货物为同一批货物且运输时限相同。

（2）腹地、中转地，以及目的地之间的运输距离和运输费用已知。同时，中转地的换装时间、费用、容量限制以及各腹地的运输需求已知。

（3）同一批货物在集运过程中每个节点最多经过一次。

（4）同一批货物仅采用一种集运方案，即同一批货物必须整批运输。

（5）同一种运输方式的平均运输速度恒定不变，不受运输路径的影响。

1.2.2 模型符号说明

1.2.3 数学模型建立

基于蓉欧+境内集疏运网络，以总成本最低建立如下目标函数：

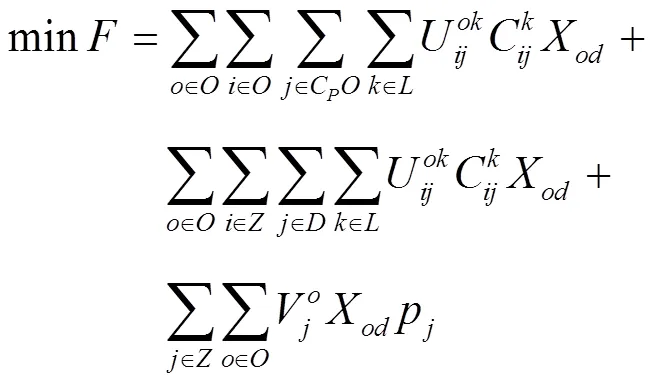
基于运输时限、路径容量限制、中转地容量限制等要求，建立如下约束条件：

（2）同一批货物不可分批运输约束，即只能采用一种运输方案，在从腹地直接运输到港口和通过中转站中转中选择一个：

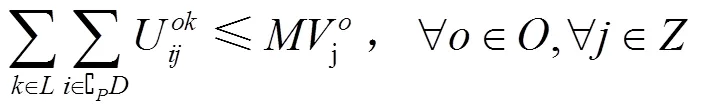
（4）中转地的流量守恒约束：

（5）运输时限约束：

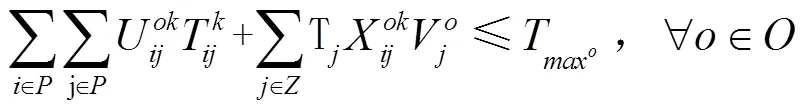
（6）腹地、中转地与目的地的定义：

（7）腹地与目的地不发生中转约束：

（8）中转地容量限制约束：

（9）流量非负约束和路径的容量限制约束：

（10）0-1约束：

2 算法设计

由于有非线性约束，若采用Lingo求解则会造成求解结果为局部最优，求解效率降低，因此本文采用遗传算法进行求解。具体步骤如下：

（1）染色体设计

染色体设计主要由两个部分组成，第一部分为编码，第二部分为解码。染色体的编码，需包括多个腹地集运方案信息，因此采用分段编码的方法。此外，染色体需包括不同腹地货物在集运过程中运输节点和运输方式选择的信息，采用整数型分阶段的编码方式，其中第一段为运输节点选择信息，第二段为运输方式选择信息。以图3的集疏运网络为例，其编码如图4所示，不仅包括不同腹地的运输节点选择信息也包括运输方式选择信息。

图3 示例图

对于染色体的解码分为两部分，第一部分为运输路径解码，第二部分为运输方式解码。运输路径解码具体如下：

图4 编码图

对于运输方式的解码，第一个运输方式的编码代表第一段路径的运输方式，依次类推。以图3腹地1的编码为例，其终点为点5。由图3知节点1的关联节点为3和4，节点1优先级最高的关联节点为点4，因此该段路径为1—4，因为4不是节点1货物的终点，因此重复步骤二与三，完整的集运方案为1—4—5，相应的运输方式为1和3，即1—4采用公路运输、4—5采用水运。

（2）初始种群，运输节点和运输方式采用随机生成的方式以保证初始种群的多样性。

（3）适应度函数，以目标函数作为其适应度函数。随机生成的运输方案满足运输需求约束，但是未考虑运力和运输时限约束，因此按照运输路径和运输方式的选择信息，对运输时间和运量进行计算，对未满足运输时限和运力约束的个体，其目标函数乘系数2作为罚函数。

（4）选择操作，本文将随机联赛策略与最佳保留策略结合，既保证了种群多样性，也可以保证最优个体被选择。具体如下：

① 最佳保留策略：将目标函数最小的个体直接保留进入下一代，不再进行交叉、变异操作，以保证最优个体被选择。

② 随机联赛策略：随机选取两个个体，比较其目标函数，目标函数较小者被选中，随后进行交叉、变异等操作。

（5）交叉操作，本文中交叉概率为0.8，路径阶段采用多点交叉的方式，运输方式采用单点交叉的方式。

（6）变异操作，采用单点变异的方法，在本文中变异概率为0.01。

（7）迭代终止条件检验，若达到最大迭代次数，则算法终止，否则，返回第三步。

3 仿真模型运行及结果分析

3.1 蓉欧+集疏运系统基本数据

为了使腹地与中转地划分明确，针对武汉与上海增设虚拟腹地，到其他节点的距离、时间以及运费与实际腹地相同。本文中集装箱均为20 ft集装箱，公路运输单位集装箱成本约为4.8元/km，水运则为1元/km[15]，铁路运输成本采用中国国家铁路集团有限公司官网的铁路货运基价表进行计算[16]。对于时间的计算，公路运输为地图导航时间，铁路与水运为距离除以平均速度（铁路、水运平均速度分别为55和35 km/h）；对于容量限制，公路运输在两节点之间没有限制。同时，各节点间的编号如图2所示，具体运输成本、运输时间与容量如表1所示，各中转地的容量限制、换装费用与换装时间如表2所示。根据中欧班列（成都）发展规划，对于腹地昆明、贵阳、重庆、武汉、厦门、上海、广州、南宁、天津、日照、宁波，平均每天的运输需求约为35、38、40、24、22、24、26、22、26、14、22TEU。

表1 各节点之间集装箱运输成本（元/TEU）/运输时间（h）/容量（TEU）

续表1

节点编号 12131415 1119 033.2/20.624 204.8/9.821 088.64/2.89 508.32/21.52 26 076.06/38.76/403 382.06/27.1/1101 440.88/20.51/1206 754.12/36.02/92 3—1 269.8/36.28/98226.8/6.48/100— 1210/04 983.34/14.138 864.96/19.971 388.16/3.33 20/04 226.75/21.6/886 952.06/38.05/841 269/6.13/100 30/01 540/44/50/862 583/73.8/82—

注：公路运输容量没有限制，表格中的数据为两项；“—”表示该节点没有水运可以到达。

表2 中转地数据

3.2 集疏运仿真分析

本文所有试验在MATLAB2017进行，在所有实验中初始种群为180，遗传代数为800，交叉概率为0.8，变异概率为0.1。在四川省周边地区集运实验中有昆明、贵阳、重庆、武汉4个腹地，泸州港一个中转地。在全国地区集运实验中，有昆明、贵阳、重庆、武汉、厦门、上海、广州、南宁、天津、日照、宁波11个腹地，泸州港、上海和武汉3个中转地。

3.2.1 模型有效性验证

在只有公路运输可以达到运输时限要求的前提下，分别进行腹地范围为四川省周边地区与全国地区的实验。其中腹地范围为四川省周边地区的实验称为四川省周边地区集运实验1，腹地范围为全国地区的实验称为全国地区集运实验1。

因为只有公路运输可以达到运输时限要求，因此其集运方案为通过公路直达到成都国际铁路港。四川省周边地区集运实验1和全国集运实验1的实验结果如表3、图5和图6所示，即通过公路直达到成都国际铁路港，与预设的运输方案相同，因此该模型与算法可行。

表3 模型有效性验证实验

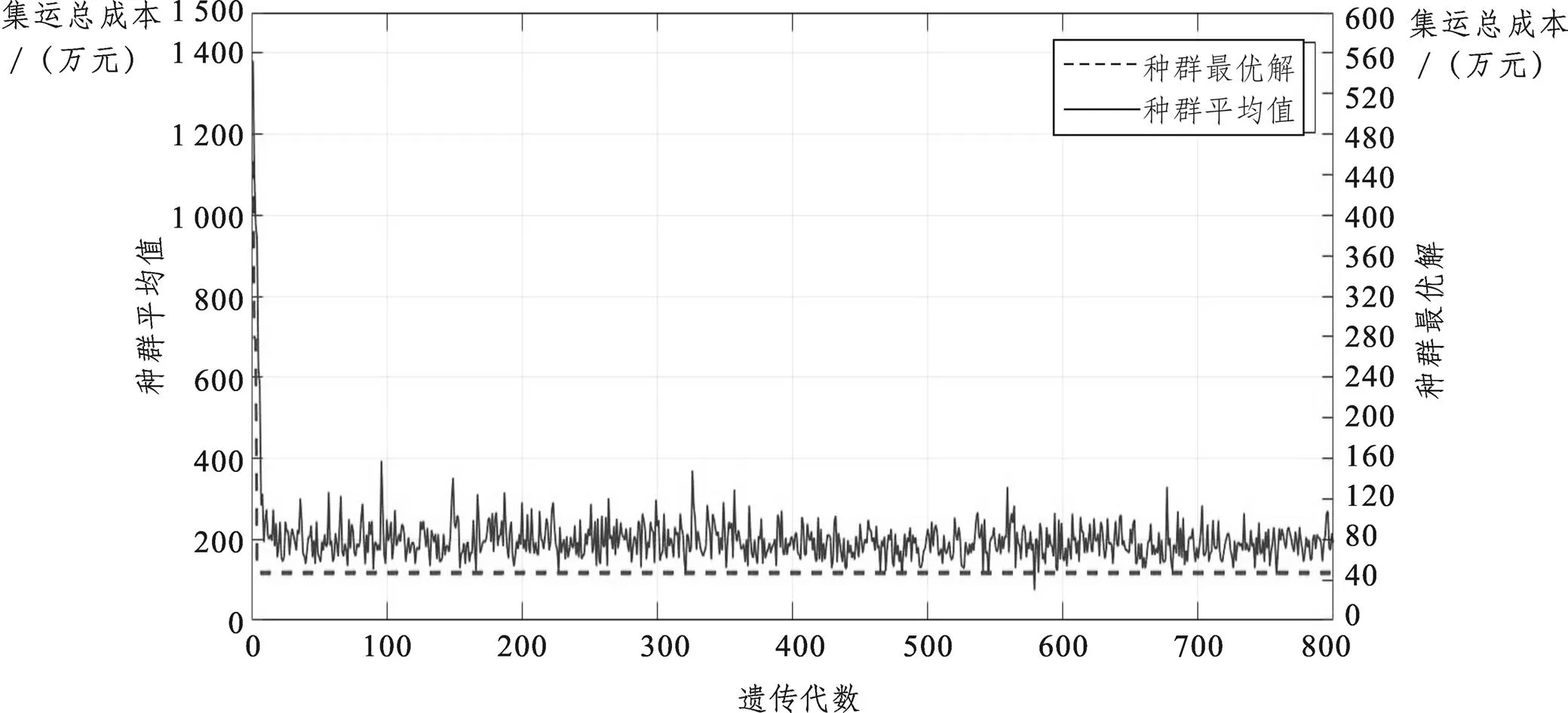
图5 四川省周边地区集运实验1

图6 全国地区集运实验1

3.2.2 数值实验

随着中欧班列（成都）的发展和腹地范围的不断扩大，因此有必要对不同腹地范围进行实验。在本节中针对蓉欧+境内集疏运系统，分别进行四川省周边地区集运实验2和全国地区集运实验2，除改变运输时限外，其他参数选取同四川省周边地区集运实验1和全国集运实验1，实验结果如表4、图7和图8所示。

表4 数值实验

续表4

实验编号腹地运输时限/h总成本/万元单位集运成本/（元/TEU·km）运输方案运输时间/h 全国集运实验21150111.760.151—15（铁路）20.82 21502—15（铁路）12.09 31503—15（铁路）5.53 41504—12—15（水运—铁路）55.87 51505—13—12—15（水运—水运—公路）107.70 61506—12—15（水运—铁路）85.67 71507—14—12—15（水运—水运—铁路）116.91 81508—15（铁路）26.2 91509—14—— 12—15（水运—水运—铁路）127.65 1015010—13—12—15（水运—水运—公路）95 1115011—13—12—15（水运—水运—公路）93.84

图8 全国地区集运实验2

将四川省周边地区集运实验1与2、全国地区集运实验1与2分别进行对比分析，发现单位集装箱运输成本减少39%、62.5%，随着腹地范围的不断扩大，单位集疏运成本减少比例更多。随着腹地范围的扩大，对于时限要求不高的货物，若一味追求时间竞争优势，会成倍增加集疏运系统的成本，凸显中欧班列（成都）的劣势。所以对于蓉欧+集疏运系统，有必要对不同运输时限要求下的货物进行优化和仿真分析。

3.2.3 全国地区集疏运仿真分析

基于前文的分析，本文在不同的运输时限要求进行仿真实验，实验结果如表5和图9所示。由图9知随着运输期限的不断延长，集运成本逐渐降低，由实验1到4知集运成本降低的主要原因是由公路运输转为铁路运输，由实验4到9知集运成本降低的主要原因是通过上海、武汉等地进行中转，具体分析如下：

表5 全国集运实验数据

续表5

实验编号节点编号运输时限/h集运成本/万元运输方案运输时间/h 5660.62129.916—13—15（水运—铁路）59.57 7116.167—14—12—15（水运—水运—公路）114.26 853.558—15（铁路）26.2 9129.259—14—12—15（水运—水运—铁路）127.65 1059.210—13—15（水运—公路）56.61 1171.5211—13—15（水运—铁路）65.61 6160.43127.351—15（铁路）20.82 247.22—15（铁路）12.09 343.483—15（铁路）5.53 472.334—12—15（水运—铁路）55.87 582.165—13—12—15（铁路—水运—公路）76.12 670.626—13—15（水运—铁路）59.57 7126.167—14—12—15（水运—水运—铁路）116.91 863.558—15（铁路）26.2 9139.259—14—12—15（水运—水运—铁路）127.65 1069.210—13—15（水运—铁路）68.77 1181.5211—13—12—15（铁路—水运—铁路）76.99 7170.43127.351—15（铁路）20.82 257.22—15（铁路）12.09 353.483—15（铁路）5.53 482.334—12—15（水运—铁路）55.87 592.165—13—12—15（铁路—水运—公路）76.12 680.626—13—15（水运—铁路）59.57 7141.77—14—12—15（水运—水运—铁路）116.91 873.558—15（铁路）26.2 9149.29—14—12—15（水运—水运—铁路）127.65 1079.210—13—15（水运—铁路）68.77 1191.5211—13—12—15（铁路—水运—铁路）76.99 8180.43118.171—15（铁路）20.82 267.22—15（铁路）12.09 363.483—15（铁路）5.53 492.334—12—15（水运—铁路）55.87 5102.165—13—12—15（铁路—水运—公路）76.12 690.626—12—15（水运—铁路）85.67 7151.77—14—12—15（水运—水运—铁路）116.91 883.558—15（铁路）26.2 9159.29—14—12—15（水运—水运—铁路）127.65 1089.210—13—15（水运—铁路）68.77 11101.5211—13—12—15（水运—水运—铁路）96.99 9190.43111.761—15（铁路）20.82 277.22—15（铁路）12.09 373.483—15（铁路）5.53 4102.334—12—15（水运—铁路）55.87 5112.165—13—12—15（水运—水运—公路）107.70 690.626—12—15（水运—铁路）85.67 7151.77—14—12—15（水运—水运—铁路）116.91 883.558—15（铁路）26.2 9159.29—14—12—15（水运—水运—铁路）127.65 1099.210—13—12—15（水运—水运—公路）95 11101.5211—13—12—15（水运—水运—公路）93.84

（1）对比分析实验1、2、3、4、5，知对于腹地1、2、3、8，除运输时限在公路运输范围之内，即小于20.82、12.09、5.53、26.2时都采用铁路直达运输方案。腹地1、2、3的货物若在泸州港进行中转最后到达成都国际铁路港，则中转费用与运输费用之和大于铁路直达运输费用，故采用铁路直达运输。对于腹地8，由于其距武汉和上海较远，即使通过水铁联运到达成都国际铁路港，但是总的成本仍高于铁路直达运输。因此，对于腹地昆明、重庆、贵阳、南宁，当运输时限大于等于20.82、12.09、5.53、26.2时，都采用铁路直达的运输方式。铁路运输满足的运输时限区间长度最长，应高度重视铁路集疏运方式的发展，降低集疏运成本。

（2）对比分析实验4、5、6、7、8、9，知对于腹地5、10、11的运输方案一直在改变，主要原因是其距武汉、上海较近，先通过铁路、公路或水运到达武汉或者上海，再通过水运到达泸州港，最后到达成都国际铁路港的运输费用小于铁路运输的直达费用。因此腹地5、10、11到达成都国际铁路港的铁路容量只需满足46.18~71.73、37.85~56.61、20.82~76.99的运输需求即可，当运输时限分别大于等于71.73、56.61、76.99时，可采用水铁联运或者公水联运到达成都国际铁路港。因此，对于腹地厦门、日照、宁波，应注意与武汉及泸州港之间的合作联系，充分利用长江内河水运系统，走多式联运之路降低成本。

（3）对比分析实验4、5，知对于腹地4与6，分别在实验4与5时，运输方案发生改变，具体的运输方案为先通过水运到达泸州港进行中转，最后到达成都国际铁路港。腹地4、6，运输时限分别在24~55.87、35.93~47.41时采用铁路直达运输，当运输时限分别大于等于55.87、47.41时采用铁水联运或者公水联运的方式到达成都国际铁路港。故上海与武汉，不仅要注意铁路集疏运方式，同时要注意与泸州港的合作，利用铁水联运降低集疏运成本。

（4）对比分析实验4、5、6，知对于腹地7、9在实验5时运输方案发生改变，具体的运输方案为先通过水运到达上海或武汉，然后在泸州港进行中转，最后到达成都国际铁路港，实际运输时间为114.26、127.65。此外，对于腹地7、9，货物的运输时限分别在27.45~114.2、34.29~127.65时，均没有采用公路或铁路先到武汉或上海进行中转的运输方案，原因是其距中转地距离居中，但若通过铁路或公路到达武汉或上海的运输成本已经超过铁路直达的运输费用。因此，广州、天津的货物运输时限在27.45~114.26、34.29~127.65时，应采用铁路集疏运方式。此外，当运输时限分别大于等于114.26、127.65时，通过武汉、上海、泸州港实现水铁联运，降低成本。故广州和天津不仅要注重铁路集疏运方式，同时要注意上海、武汉、泸州港之间的合作，充分利用铁水联运降低集疏运成本。

综上所述，对于昆明、贵阳、重庆、南宁，其集运成本的降低主要通过采取铁路运输的方式，相比于其他腹地其铁路运输满足运输时限的区间最长，应高度重视铁路集疏运方式。对于上海与武汉，随着运输时限的延长，集疏运成本降低的主要原因为通过泸州港实现铁水联运，故武汉与上海的应注意与泸州港之间的合作，充分利用长江内河水运通道，降低集疏运成本。对于日照、广州、天津、厦门、宁波，其集疏运成本的降低主要原因在于通过武汉和上海进行中转，应注意与武汉以及上海的联系，尤其对于厦门、宁波和日照，对比与其他腹地其铁路运输满足运输时限的区间长度较短，应高度重视与武汉、上海之间的合作。此外，由于在上海与武汉进行中转后，要通过泸州港进行中转，最后到达成都国际铁路港，因此也应重视与泸州港之间的合作。

4 结束语

本文以蓉欧+境内集疏运系统为研究对象，在考虑中欧班列（成都）所处的发展现状及集疏运系统存在问题的背景下建立数学模型。在不同运输时限下进行实验，对不同类型的腹地分别提出优化建议，具体为：对于距离成都国际铁路港较近的腹地如昆明、重庆、贵阳，或者进行中转运输费用较高的腹地如南宁，都应高度重视铁路集疏运的方式，从而降低集疏运成本；对于距离中转地较近、运输时间短、运输费用比较低的腹地如厦门、宁波、日照，应注重与武汉、上海等中转地之间的合作，充分利用长江内河水运通道，通过多式联运降低集疏运成本；对于距离中转地居中的如广州、天津腹地，不仅要注重铁路集疏运方式的发展，而且应注重与武汉、上海等中转地之间的合作，同时利用铁路与水运降低集疏运成本。本文在中欧班列（成都）发展的初步阶段，以成本最小为目标函数，在未来的研究中，在本次研究的基础上，将运输安全与运输质量等指标在模型中予以体现，提高运输质量。此外，蓉欧+境内集疏运系统庞大复杂，具有很多不确定的因素，在今后的研究中，将考虑这些不确定因素的影响，如货运需求的波动。

[1] DE LANGEN P W, FRANSOO J C, van Rooy B. Business models and network design in hinterland transport[M]. Springer New York, Handbook of Global Logistics, 2013: 367-389.

[2] 臧白鸽. 集装箱港口内陆集疏运网络优化[D]. 大连：大连海事大学, 2011.

[3] 江建宇. 共享腹地港口群集疏运系统智能体仿真研究[D]. 广州：华南理工大学, 2014.

[4] 黄芳, 陶杰. 港口物流集疏运系统网络结构优化分析[J]. 交通运输工程与信息学报, 2007, (2): 80-83, 114

[5] 李斌. 基于计算物流的集装箱码头集疏运虚拟机体系结构及其仿真分析[J]. 计算机集成制造系统, 2018, 24 (1): 245-263.

[6] 李斌, 李文锋. 基于MAS的集装箱码头物流系统协同生产调度体系[J]. 计算机集成制造系统, 2011, 16 (11): 2502-2513.

[7] HUANG S Y, HSU W J, CHEN C, et al. Capacity analysis of container terminals using simulation techniques[J]. International Journal of Computer Applications in Technology, 2008, 32 (4): 246-253.

[8] CHU Chin-yuan, HUANG Wen-chin. Determining container terminal capacity on the basis of an adopted yard handling system[J]. Transport Review, 2005, 25 (2): 181- 199.

[9] 许欢, 刘伟, 刘诗. 低碳经济下的港口泊位分配模型及其算法实现[J]. 计算机工程与应用, 2014, 50 (6): 219-225

[10] CHANG T S. Best routes selection in international intermodal networks [J]. Journal of Dalian Maritime University, 2013, 35 (9): 2877-2891.

[11] HAO C, YUE Y. Optimization on combination of transport routes and modes on dynamic programming for a container multimodal transport system [J]. Procedia Engineering, 2016, 137: 382-390.

[12] 冯震, 刘佳, 李靖, 等. 复杂网络中最短路径问题的求解算法研究[J]. 自动化技术与应用, 2010, 29 (3): 32-35, 43.

[13] 蒋先稳, 孟燕萍. 港内集装箱码头腹地和转运业务竞合研究[J]. 计算机工程与应用, 2019, 55 (10): 225-232, 263.

[14] 孟良. “蓉欧+”助推成都加速融入亚欧经济新版图[J]. 大陆桥视野, 2016 (10): 63-65.

[15] 孙昕. 宁波-舟山港集装箱内陆集疏运网络优化研究[D]. 舟山: 浙江海洋大学, 2016.

[16] 岳鑫, 尹传忠, 武中凯. 洋山港集装箱集疏运网络优化研究[J]. 铁道运输与经济, 2019, 41 (2): 11.

Optimization and Simulation of Container Collection and Distribution System of Rongou+ in China

LIU Lu-lu, TANG Yin-ying, CHEN Si

（1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China;2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Chengdu 611756, China）

With the Rongou+ development strategy, a model is established for the current development scenario of China Railway Express (Chengdu) and the problems existing in the current collection and distribution system. The objective function of the model was to have the least collection and distribution cost, and the constraint condition was the transportation time limit on goods. Based on priority piece-wise coding, the genetic algorithm was designed. Furthermore, simulation experiments were performed under different transportation time limits. The results show that: Kunming, Guiyang and Chongqing, which are close to Chengdu international railway port, should be attached great importance in terms of railway collection and distribution. Nanning which is farther away from the transit area, should be attached great importance with regard to development of railway collection and distribution modes. Xiamen, Ningbo and Rizhao, which are close to transfer places, should also be noted in cooperation with Wuhan, Shanghai and other transfer places to reduce costs through multimodal transport. Guangzhou and Tianjin, which are in the middle of the transit area, should begiven great importance not only with regard to development of railway collection and distribution modes, but also with regard to cooperation with Wuhan, Shanghai, and other transit areas.

Rongou+; transportation time limit; genetic algorithm; simulation

U169.6

A

10.3969/j.issn.1672-4747.2020.03.003

1672-4747（2020）03-0019-13

2019-11-10

西南交通大学双一流学科建设项目；中国铁路总公司科技研究开发计划重点课题（2018BX15）；教育部人文社会科学研究西部青年基金项目（16XJCZH001）；四川省哲学社会科学重点研究基地四川省农村发展研究中心项目（CR1716）

刘露露（1994—），女，陕西西安人，硕士研究生，研究方向为交通运输工程，E-mail：990972547@qq. com

陈思（1982—），女，成都人，西南交通大学交通运输与物流学院讲师、博士，研究方向为物流网络规划与设计，E-mail：chensi@swjtu. cn

刘露露，汤银英，陈思. 蓉欧+境内集装箱集疏运系统优化及仿真[J]. 交通运输工程与信息学报，2020，18（3）：19-31

（责任编辑：刘娉婷）