基于三参数区间数的编组站子系统能力协调研究

袁 野，薛 锋，户佐安，张厚红

基于三参数区间数的编组站子系统能力协调研究

袁 野1，薛 锋2,3，户佐安2，张厚红4

（1. 雄安城市规划设计研究院，绿色交通设计研究所，河北 雄安 071700；2. 西南交通大学，交通运输与物流学院，成都 611756；3. 综合交通大数据应用技术国家工程实验室，成都 611756；4. 南京铁道职业技术学院，南京 210031）

随着高速铁路逐步成网，普速铁路的运输能力得到了极大释放，铁路运输系统之间原有的平衡状态需要重新协调。对于编组站能力的既有研究，大多采用“定值”形式及“刚性”协调策略，不能有效揭示子系统的匹配变化规律。综合考虑编组站能力的波动性及动态适应性，以系统静态、动态协调为目标，构建了编组站子系统能力协调模型，并通过引入缓冲算子的功效系数法对多目标函数进行简化，利用区间占优及区间分析理论对目标函数与困难约束中的不确定性区间参数进行处理。基于双向三级六场编组站设置算例参数，并通过Lingo软件对模型进行求解，结果表明当车站上行系统列流量为136列、下行系统列流量为130列时，能够达到编组站子系统能力协调模型的最优状态，证明所用方法是一种研究编组站子系统能力的有效方法。

铁路运输；编组站能力；三参数区间数；系统协调；耦合优化；区间分析法

0 引 言

随着高速铁路的快速发展，普速铁路能力得到极大释放，货物运输格局变动较大，铁路“点-线-网”能力需重新协调匹配。编组站作为铁路网络的中间节点，其日常生产作业需要各子系统之间协调完成，而且各子系统之间也存在一定的耦合互补关系，任一环节发生问题，都会引起其前后序列系统的作业困难甚至堵塞，造成编组站能力的损失。只有当编组站各系统能力相互协调匹配时，才能最大限度地发挥各个子系统的作用。因此，如何从能力的动态适应性出发，使车站子系统的能力协调从单一孤立化上升到立体综合化，使之具有更加完善的协调机制和更灵活的应变能力，需要进一步研究。

目前，国内外对能力的研究，成果颇丰。国外发达国家的铁路能力一般较为富余，能力运用矛盾并不突出，因此国外对于铁路能力协调的直接研究成果较少。Dirnberger J. R[1]介绍了编组站的作业精简方法以便充分利用能力；Jianxin Y[2]探讨了车站能力的优化运用问题；Gabriele M等[3]采用概率等方法评估计算了复杂铁路枢纽的能力；Meng等[4]建立两阶段随机规划模型，研究了铁路、公路联运能力的协调利用及运输费用问题；Reinhardt L.B等[5]将时间以小时为单位离散化，并依据未来需求分析了铁路网络扩展的影响，并在长期战略层面提出了货物运输能力评估模型；其他国外相关领域学者习惯在解决编组站系统车流协调问题时，将各车站设备资源视作约束条件，进而转化为数学问题进行求解[6, 7]。在国内相关研究方面，薛锋等[8, 9]在不均衡运输条件下，分析了点图能力的动态协调关系，推导出了点图能力协调的状态转移方程；刘汉英等[10]为提高铁路车站咽喉区及整个车站的通过能力，运用咽喉区道岔分组简化咽喉道岔及进路优化方法对铁路车站咽喉通过能力进行了研究；赵鹏[11]对不均衡运输的背景进行了分析，并以襄樊枢纽为例，通过引入动态平衡方程对枢纽点线能力协调进行了研究；孙琦[12]提出了能力修正系数的概念，并对作业过程列车状态进行了详细说明，进一步探究了基于铁路货物运输作业过程的点线能力协调问题；田亚明、林柏梁[13, 14]结合我国铁路的运输组织特点及未来的发展方向，提出了一系列解决编组站改编能力配置优化问题的模型和方法；刘海岩[15]将编组站点线能力协调分为微观（子系统点线能力协调）和宏观（车站与衔接区间）两个层面，并建立了编组站与衔接区间点线能力协调模型；彭桢[16]针对编组站排队服务系统，采用协调度理论，分别对成都北编组站上下行各子系统及其相互之间的协调性进行了研究。

从以上研究可以发现，目前国内外对于铁路编组站能力协调方面的研究主要以编组站与衔接区间、到达系统与解体系统、阶段计划与动态车流等为对象，且大多数的模型约束都是基于能力的定值约束。在研究成果上，刚性多于柔性，静态多于动态，未能揭示能力的动态随机性。本文将区间概念引入编组站能力的表示中，并以此为基础对编组站子系统能力协调进行分析，构建编组站子系统能力协调模型，提高模型的适用性和灵活性，依托区间分析理论对模型进行处理，对编组站子系统间的协调性进行优化。

1 编组站子系统能力协调分析

编组站是一个复杂的大系统，在其内部按照作业性质又可分为若干子系统，子系统间相互协作，各自有序，共同完成整个车列改编的流水线作业，执行这些作业的各项技术设备便是构成各子系统的元素。到发系统和解编系统都是编组站列车作业系统的子系统，它们相互独立却又不可割裂，任何一个子系统内作业环节的遗漏都会对另一子系统甚至是整个编组站日常作业造成连锁影响。从列车由衔接区间接入车站开始，到由出发场发出为止，列车的任何状态变化都与车站的通过能力和改编能力戚戚相关。同时到发系统和解编系统间、通过能力与改编能力间也存在着一定的协调关系，可以从两个方面对其进行描述：

（1）从独立到整体

无论是到发系统还是解编系统都是以独立的子系统形式存在为前提的，编组站大系统的协调，需要把各个子系统通过某种方式结合到一起。通过将到发系统和解编系统进行分割研究，悉知各子系统的作业内涵及列车周转过程，确定其通过能力与改编能力的影响因素，再从整体的视角，将它们关联起来分析，以获得编组站作为一个整体的最大生产效率。

（2）从静态到动态

在最初编组站设计的过程中，就基本确定了车站的最大通过能力和改编能力。能力在一定的运输组织模式下，又可以通过负反馈进行调节，最终达到相对稳定的状态。前者是静态协调，实质上是对编组站系统布局的最优设计，后者属于动态协调，是对编组站系统作业的最优控制。

静态协调属于设计规划阶段的协调，需要考虑诸多因素，例如投资费用、建设成本、资源利用、设备配置、更新改造等。至于动态协调，其对象是编组站各作业子系统，其中到发系统和解编系统是最重要的组成部分，当编组站到发系统与解编系统列车技术作业不协调时，便会引发一系列连锁反应。当通过能力小于改编能力时，编组站发车系统不能有效疏解解编系统处理的列车，严重时会造成编组站发车系统的局部堵塞；当通过能力大于改编能力时，从区间进入编组站的列车完成接车作业后不能顺畅进入解编系统进行调车作业，进而造成车流在接车系统的车流积压，同时也会引起发车系统技术设备的资源浪费。编组站通过能力与改编能力协调作用如图1所示。

图1 通过能力与改编能力协调作用热力图

依据静态协调与动态协调关系建立编组站子系统能力协调模型，其中动态协调体现在对编组站系统作业的最优控制，静态协调体现在对编组站系统布局的最优设计。考虑通过系统与改编系统的协调程度最大（动态协调）和编组站改扩建费用最小（静态协调）两个目标，以期得出系统协调度最优时通过能力与改编能力的扩充量。对到发系统与解编系统之间的协调关系进行有效表征，以直观了解编组站车流状态和空间使用效率，对于提高整个编组站系统的生产效率，改进运输组织方式尤为重要。

考虑技术站列车作业占用时间由于列车晚点、子系统间的干扰、设备故障以及行车事故等引起的不确定性，技术站作业系统会出现空间上局部型、时间上阶段性的堵塞现象。而技术站能力也会在有条件、有边界的范围内呈现出某些幅度的摆动。能力的上极限和下极限对能力本身限定了一个范围，它的数学本质是区间。

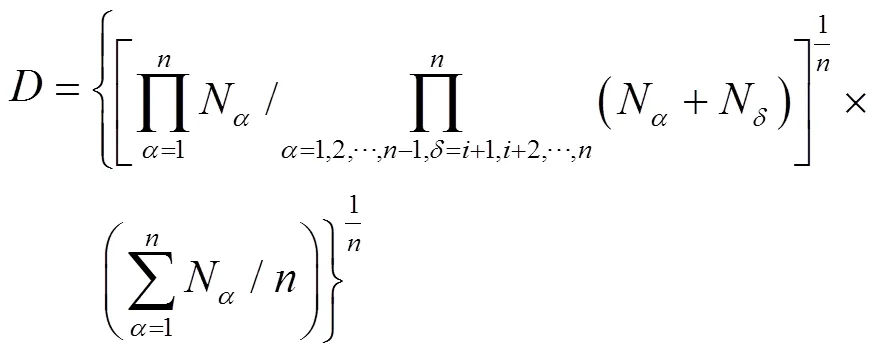
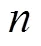
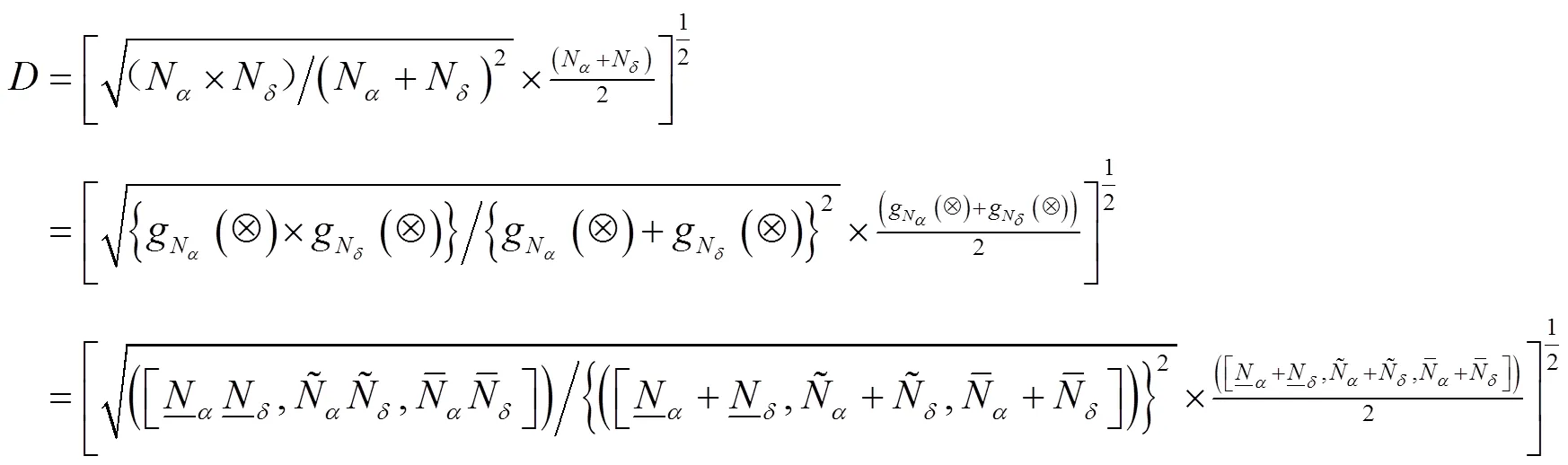
2 模型建立

2.1 决策变量

将到达与出发系统结合，表征编组站的通过能力强弱；解体系统与编组系统结合，表征编组站的改编能力大小。如果把解编系统看作一个点，那到发系统就是与点的两端相衔接的线，所以到发系统与解编系统的协调，可以看作文献[13]的变形、文献[15]的延伸。到发系统与解编系统都是车流量在一定范围波动的容器，当通过能力大于改编能力时，容器呈哑铃状；当解编能力大于通过能力时，容器呈糖果状，如图2、3所示。

图2 糖果型

图3 哑铃型

共计六个决策变量，即：

2.2 目标函数

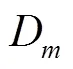
目标函数1 编组站上、下行改编系统和通过系统的协调程度最大：

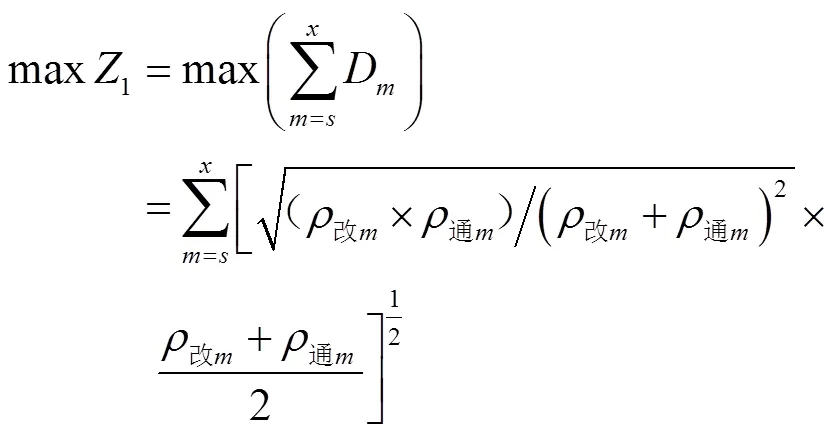
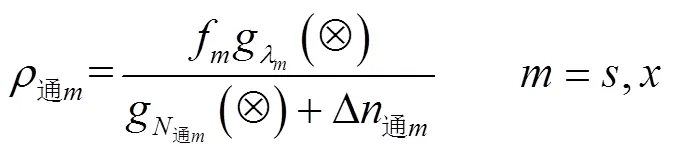
目标函数2 编组站改扩建投资费用最小：

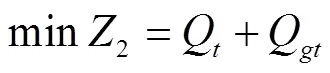
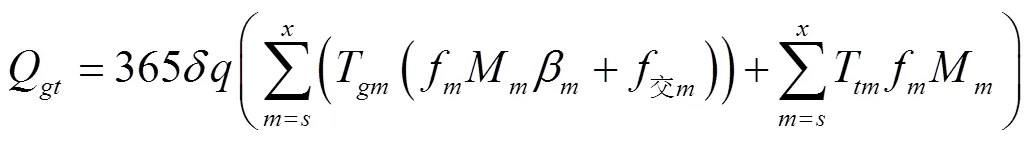
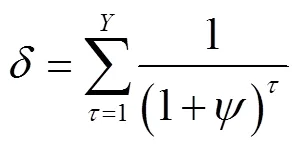
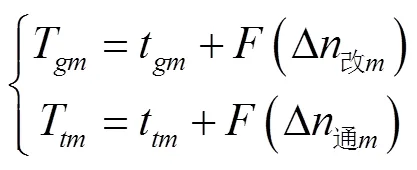
2.3 约束条件

综合考虑编组站上、下系统通过能力、改编能力、扩能限制等，MSSCCM的约束条件包括：

（1）编组站上、下行系统的通过能力约束

编组站到发系统实际办理的总列流量不超过编组站的实际通过能力：

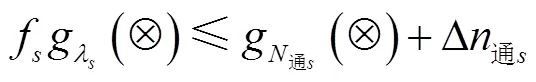
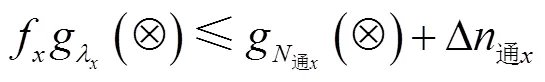
（2）编组站上、下行系统的改编能力约束

编组站解编系统实际办理的总车流量不超过编组站的实际改编能力：

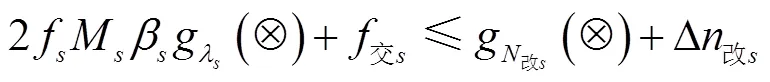
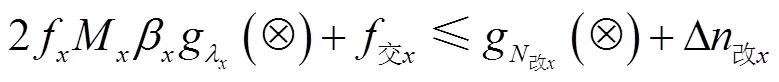
（3）货运运输需求量约束

编组站办理的实际车流量不应小于货物运输计划的需求：

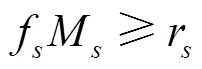
（4）编组站改编能力扩充量约束

由于地形、成本等因素，编组站改编能力扩充量存在一定的扩充上限，而在实际中，编组站改编能力都是成规模进行扩充的，因此也存在一定的扩能下限，因此编组站改编能力扩充量约束如下：

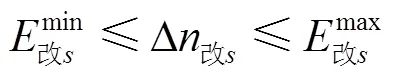
（5）编组站通过能力扩充量约束

与改编能力类似的，编组站通过能力扩充量约束如下：

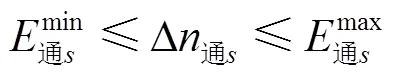
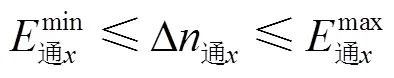
3 模型的求解方法

3.1 多目标函数问题的处理

MSSCCM属于多目标优化问题，而一般多目标优化问题的各目标间并非是统一的，可能存在一定矛盾，如何对各个子目标进行协调权衡和折中处理是解决多目标优化问题的关键。通常，一般的解决思路是将多目标问题转化为单目标问题进行处理，通过求出单目标问题的最优解作为多目标问题的解，但MSSCCM中的两个目标量纲并不统一，采用功效系数法对目标函数进行标准化处理再进行求解往往能够避免目标数量级差异引起的结果误差，从而起到较好的效果。

功效函数可以由下式表示：

功效函数可以由下式表示：

如此多目标问题可以转化为单目标问题：

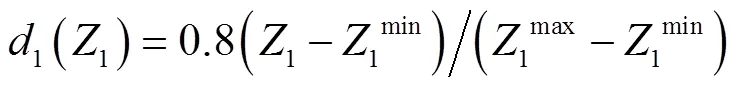
3.2 目标函数与困难约束中区间参数的处理

对于不确定性多目标优化问题的一般模型GM形式表示如下：

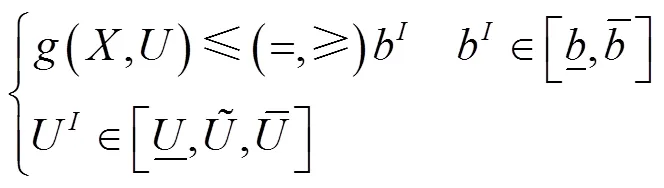
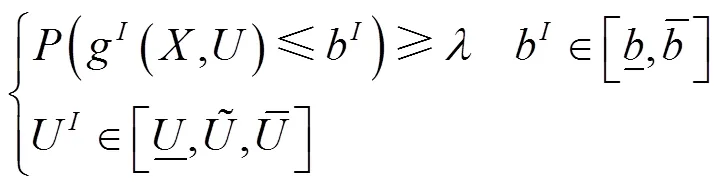
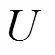
根据自然区间扩展[18]可得到约束条件的区间，如下所示：

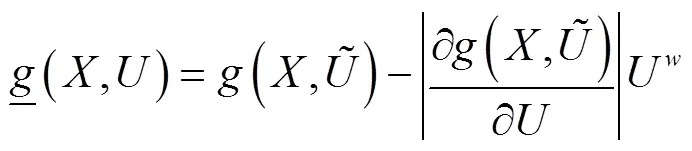
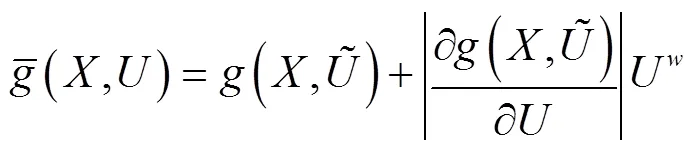
因此，对MSSCCM来说，其目标函数1可以转化为：

其约束条件1、2可以转化为：

通过区间分析方法进一步展开可得：

4 算例分析

为了更加清晰地对模型进行说明，本文基于双向三级六场编组站设置算例，相关参数如表1所示。

表1 算例车站相关参数表

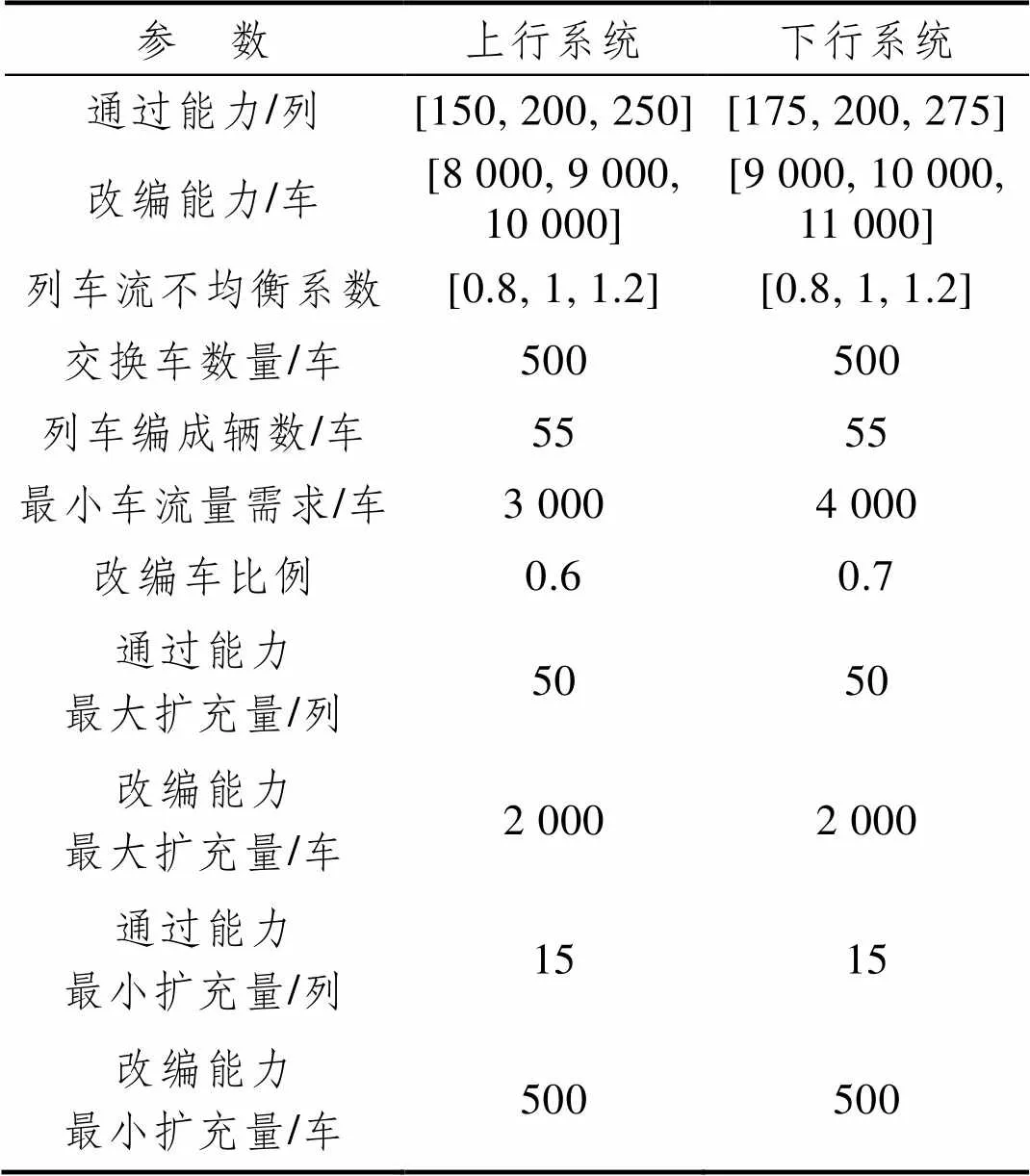
Tab.1 Example station related parameter list

利用MSSCCM对问题进行求解，通过Lingo对模型进行计算，得到车站上行系统列流量为136列、下行系统列流量为130列时，能够达到编组站子系统能力协调模型的最优状态。此时上行系统需要的通过能力扩充量为15列，改编能力扩充量为500辆；下行系统通过能力扩充量为15列，改编能力扩充量为510辆。上行系统的耦合协调度达到了0.630，下行系统的耦合协调度达到了0.623，而不考虑改扩建经济因素，上行系统的耦合协调度能够达到0.650，此时列流量为155列，通过能力扩充量为17列，改编能力扩充量为1 730辆；下行系统的耦合协调度能够达到0.645，此时列流量为149列，通过能力扩充量为15列，改编能力扩充量为1 973辆。可见经济因素的限制对编组站改扩建及子系统协调程度的影响，可为铁路编组站相关运营管理部门提供决策依据。

5 结束语

本文分析了编组站的系统协调情况，并依据静态协调与动态协调关系建立了编组站子系统能力协调模型，模型中考虑了通过系统与改编系统的协调程度（动态协调）最大和编组站改扩建费用最小（静态协调）两个目标，将三参数区间能力应用于模型中，并设置算例验证了模型的有效性，得出以下结论：

（1）将三参数区间通过能力和改编能力应用于模型的目标函数和约束条件中，形成能力动态约束的编组站子系统能力协调模型，通过功效系数法对多目标函数进行了处理，并应用区间占优及区间分析理论对目标函数和困难约束中的不确定区间参数进行处理，这种方法是可行的，为之后模型的求解提供了便利条件。

（2）通过设置双向三级六场编组站的算例，并利用Lingo对模型进行计算，得出相关数据：车站上、下行系统的列流量为136列、130列时，能够达到编组站子系统能力协调模型的最优状态，此时上、下行系统需要的通过能力扩充量均为15列，改编能力扩充量为500辆和510辆。上、下行系统的耦合协调度分别达到了0.630和0.623，体现了能力区间数作为约束条件的良好适应性与灵活性。

铁路运输系统的协调需要考虑的因素很多，任何子系统内部的设施设备、运力资源以及“点-线-网”系统之间都存在很强的关联性。本文的研究局限于编组站内部作业系统间的动态协调，只有当“点-线-网”能力动态性均得到良好的协调匹配时才能发挥铁路运输系统的最大效益，这需要进一步深入研究。

[1] DIRNBERGER J R. Development and application of lean railroading to improve classification terminal performance [D]. Urbana-Champaign: University of Illinois, 2006.

[2] YUAN J X, INGO A H. Optimizing capacity utilization of stations by estimating knock-on train delays[J]. Transportation Research Part B, 2007, 41(2): 202-217.

[3] GABRIELE M, TATIANA M, STEFANO R, et al. A synthetic approach to the evaluation of the carrying capacity of complex railway nodes[J]. Journal of Rail Transport Planning & Management, 2014, 4 (1): 28-42.

[4] MENG Q, HEI X L, WANG S A, et al. Carrying capacity procurement of rail and shipping services for automobile delivery with uncertain demand[J]. Transportation Research Part E, 2015, 82 (10): 38-54.

[5] REINHARDT L B, PISINGER D, LUSBY R. Railway capacity and expansion analysis using time discretized paths[J]. Flexible Services and Manufacturing Journal, 2018, 30(4): 712-739.

[6] MINYOUNG P. Capacity modeling for multimodal freight transportation networks[D]. Irvine: the University of California, 2005.

[7] Cambridge Systematic, Inc. NCHRP. Multimodal corridor and capacity analysis manual[R]. Washington D. C.: TRB, National Research Council, 1998.

[8] 薛锋, 罗建. 编组站能力与运行图能力的动态协调关系[J]. 铁道运输与经济, 2008, 30 (7): 76-79.

[9] 薛锋, 王慈光, 张展杰. 编组站配流的协调优化算法[J]. 西南交通大学学报, 2010, 45 (6): 932-937.

[10] 刘汉英, 刘斌. 铁路车站咽喉通过能力分析研究[J]. 铁道运输与经济, 2018, 40(8): 12-16.

[11] 赵鹏. 铁路枢纽点线能力协调性研究[D]. 长沙: 中南大学, 2010.

[12] 孙琦. 基于铁路货物运输作业过程的点线能力协调问题研究[D]. 北京: 北京交通大学, 2010.

[13] 田亚明. 铁路网编组站改编能力配置优化研究[D]. 北京: 北京交通大学, 2012.

[14] 田亚明, 林柏梁. 既有线运能释放及机车交路延长条件下编组站改编能力配置的优化[J]. 中国铁道科学, 2015, 36 (1): 119-125.

[15] 刘海岩. 编组站点线能力协调研究[D]. 北京: 北京交通大学, 2012.

[16] 彭桢. “CIPS”环境下成都北编组站能力协调研究[D]. 成都: 西南交通大学, 2017.

[17] QIU Z P. Comparison of static response of structures using convex models and interval analysis method[J]. International Journal for Numerical Methods in Engineering, 2003, 56 (12): 1735-1753.

[18] RAMON E M. Methods and applications of interval analysis[M]. Philadelphia: Society for Industrial Mathematics, 1979.

Marshalling Station Subsystem Capacity Coordination Based on Three-parameter Interval Numbers

YUAN Ye1，XUE Feng2, 3，HU Zuo-an2，ZHANG Hou-hong4

（1. Green Traffic Design Office, Xiong’an Urban Planning and Design Research Institute, Xiong’an 071700, China；2. School of Transportation and Logistics，Southwest Jiaotong University, Chengdu 611756, China；3. National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Chengdu 611756, China;4. Nanjing Institute of Railway Technology, Nanjing 210031, China）

With the formation of high-speed railway networks, the capacity of existing railways has been greatly[A8] . Consequently, the original balance among railway transportation systems needs to be reconciled. Most existing research on the capacity of marshalling stations uses a “fixed value” representation and a “rigidity” coordination strategy, which cannot effectively reveal the[A9] . By considering the capacity volatility and dynamic adaptability of the marshalling station and by[A10] , a marshalling station subsystem capacity coordination model is developed. The multi-objective function is simplified by using the efficiency coefficient method. The uncertainty parameters in the objective function and the[A11] constraints are processed by employing interval analysis theory. Example parameters are set based on[A12][A13] . The results show that an optimal state of the marshalling station subsystem capacity coordination model can be achieved when the station uplink system wagon flow is 136 and the downlink system wagon flow is 130. This can be an effective measurement for studying marshalling station subsystem capacity.

railway transportation; marshalling station capacity; three-parameter interval numbers; system coordination; coupling optimization; interval analysis method

U292.5

A

10.3969/j.issn.1672-4747.2020.03.010

1672-4747（2020）03-0083-10

2019-11-15

国家自然科学基金项目（61203175）；四川省科技计划项目（2019YJ0211）；综合交通大数据应用技术国家工程实验室开放基金项目（CTBDAT201902，CTBDAT201911）

袁野（1994—），男，河北沧州人，工学硕士，研究方向：交通运输规划与管理，E-mail：43617464@qq.com

薛锋（1981—），男，山东邹城人，西南交通大学副教授，工学博士，从事运输组织理论与系统优化、铁路运输信息技术研究，E-mail：xuefeng.7@163.com

袁野，薛锋，户佐安，等. 基于三参数区间数的编组站子系统能力协调研究[J]. 交通运输工程与信息学报，2020，18（3）：00-00

（责任编辑：李愈）