隐藏于三角函数中的“向量思想”

罗世评

江西省南昌市湾里区第一中学 (330004)

首先将利用向量思想推导任意两角差的余弦公式及“辅助角”公式如下：

结论1任意两角差的余弦公式cos(α-β)=cosαcosβ+sinαsinβ其中(α∈R,β∈R).

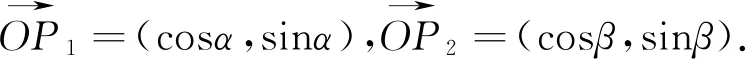
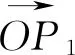
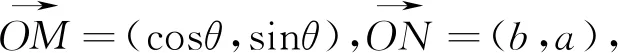
从上述两个结论推导过程可以看出用向量思想来解决三角问题能获得意想不到的效果，该公式的推导思路使学生能够更好的理解“辅助角”公式的由来，也为后期更好应用该公式打下良好基础.也体现了采用向量思想在三角中的重要地位.

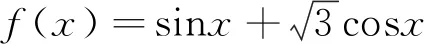
分析：本例题来源于北师大版教材第三章第二节部分，教材中采用特殊角三角函数值、正弦两角和公式及正弦函数性质相关知识进行求解.根据本题给出的形式，不妨采用上述结论2中的向量思想求解，将会取得比较好的效果.

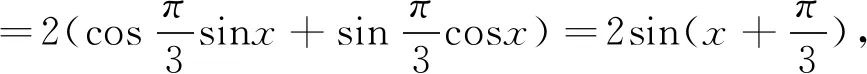
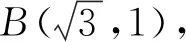
我们不妨对上述两种“解题思路”进行分析，教材中给出的解法着重强调对两角和差公式的结构理解和掌握，同时要求学生在“拼凑”两角和差公式的过程中能灵活应用特殊角三角函数值,再利用正弦函数性质给出结论.而向量思想侧重考察“转化”思想，将如形asinθ±bcosθ的表达式，采用向量数量积运算来表示对应的函数，这将为解决函数最值或取值范围问题提供更有效的方法.

分析:通过适当的化简得3ycosx-2sinx=4y-3，该式左边形如asinθ±bcosθ的形式，满足引例中的向量思想解答本题.

解析:由题意可知x∈R，原式可化为y(3cosx-4)=2sinx-3，即3ycosx-2sinx=4y-3.

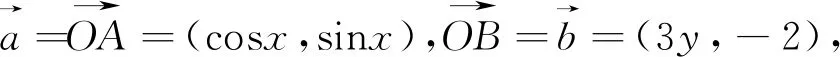
解析:由题意易知y>0，原式可化简为ysinx=2-cosx，即ysinx+cosx=2.

例3 (教材改编)若关于x的方程(2k+3)sinx+kcosx=k+3有实根，求实数k的取值范围.

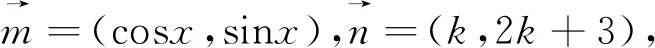
从上面的3个例题中我们不难发现，如将三角问题进行适当的化简处理，使原式转化成形如asinθ±bcosθ的形式，使用向量思想也将可以完美解决函数最值或取值范围相关问题，并得到取等号时的对应条件.这使得我们在实际教学中，面对“辅助角”公式的理解和应用感到困惑的学生，提供了一条不错的途径.

分析:考虑到使用向量思想表示函数，不妨将原式变形为求f(x)-1=(1+sinx)(1+cosx)，利用单位圆，把函数取值与相应四边形或三角形面积联系起来考虑，通过求面积大小来得到f(x)最值.

图1

解析:如图1，在单位圆和直角坐标系中，不妨记

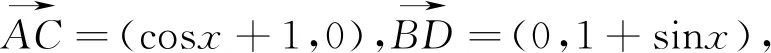
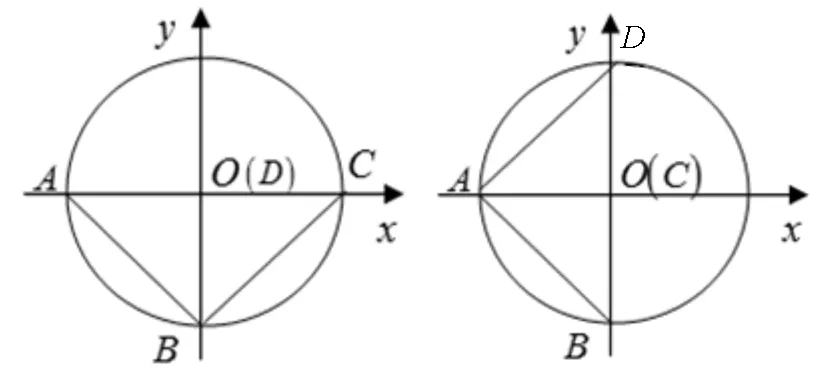
图2 图3

例5 (2018年全国Ⅰ理科)已知函数f(x)=2sinx+sin2x，则f(x)的最小值.

分析:通过化简知f(x)=2sinx(1+cosx),从形式看和例4有类似之处，利用单位圆，可将函数f(x)取值与对应的三角形ΔABC面积联系起来，利用三角形面积最值问题来求解f(x)的最小值.

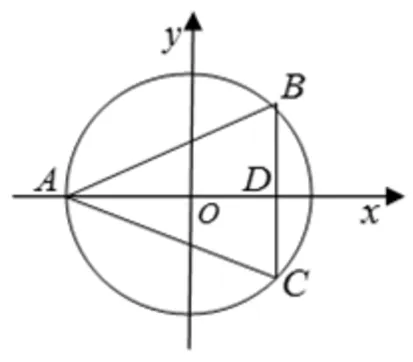
图4

解析:如图4，通过单位圆不妨A(-1,0),B(cosx,sinx)，C(cosx,-sinx)，

评注：从以上例4、例5应用向量思想求解三角问题的过程可以看出，当我们恰当的利用单位圆上点坐标的特点和向量相关知识，使得三角函数问题与对应的几何图形面积联系起来，从而为我们提供了一种用几何方式解答三角问题的重要思想.