数学“解题教学”的实践与反思

丁称兴

江苏省溧水高级中学 (211200)

“解题是数学的心脏”，学习数学，关键之一就是要学会解题.所谓“解题”，就是揭开“条件”与“结论”之间的内在联系，或是探索“已知”如何导出“未知”.数学解题通常有四个阶段：理解题意→思路探究→书写解答→回顾反思.理解题意就是审题，这是整个解题工作的第一步，而且贯穿于解题的始终.思路探究就是寻找从“已知”到“未知”的方法与途径.笔者认为：好的解题教学应从以下几个方面来开展.

一、要突出学生学习的主体地位

课堂教学的目的，在提高学生知识水平的同时，也要提高学生的数学素养和数学能力.在课堂教学中，要通过教学设计，引导学生积极参与问题的分析、解决过程，更要鼓励学生积极思考，从多角度思考问题.

课堂上笔者给出这道例题后，学生给出了以下几种解法.

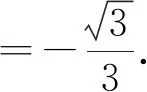
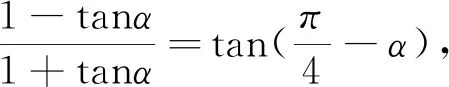
方法4：由于(sin15°-cos15°)×(sin15°+cos15°)=sin215°-cos215°=-cos30°，所以原式的分子、分母同时乘以sin15°-cos15°得

还“老师的精辟分析、讲解”于“学生的自主思考、探究”，做到教师主导与学生主体有机结合.多种解法揭示问题的本质：化“非特殊角”为“特殊角”，体现了转化的数学思想.在教学中能够通过问题的解决揭示数学问题的本质，就能让学生具有一双透过现象看本质的“慧眼”，学生的思维能力就能得到充分的发展，使问题的解决变得简单而自然.

二、教会学生思考问题

1.扎实的基础才能产生丰富的联想

波利亚说：货源充足和组织良好的知识仓库是一个解题者的重要资本.数学是充满联系的科学，我们应该抓住一切可能的联系进行联想与转化.引导学生学会联想和转化是提高解题能力和认识数学思维特征的一个重要方法.

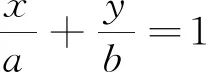
A.a2+b2≤1B.a2+b2≥1

分析1：大部分学生看题后第一反应是把点M代入直线方程，再想下一步.注意到等式中正、余弦的线性结构关系，可联想用辅助角公式合并化简求解.

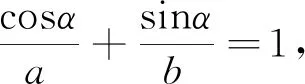
分析2:联想圆的参数方程，转化成直线与圆的位置关系问题.

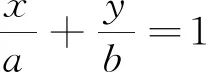
分析3：观察四个选项的二次特征，联想柯西不等式进行正余弦和参数a,b的分离.

解题教学中，我们不仅需要关注这道题目怎么解，更需要关注这道题目所蕴含了哪些知识与方法.通过对这道题目的深入研究，学生能很好地对原有知识体系进行查漏补缺，达到一题迁移一片，解决一类题的目的.

2.解题分析起步于观察角度的变化

观察是指有目的、有计划、较持久的知觉过程，观察具有目的性、客观性、敏锐性、精细性和全面性.解题分析起步于对问题的有效感知与观察，只要善于变换角度，仔细观察，抓住要害特征，联想大脑里已存在的知识与技能信息，就能较快地形成解题方案.

解题教学中,教师必须让学生真正参与其中,及时地根据学生的信息反馈,对解题过程做出正确调控,尽量沿着学生的思维轨迹,对思维开展做出调控.特别是当学生的思路与教师原先的设想有差距,但对深入地理解问题又具有一定价值时,教师要因势利导,帮助学生分析思路受阻的原因,教会学生寻求出路的方法,引导学生分析方法的优劣.只有这样,才能使不同层次的学生的解题能力得以提高.

3.教师真实暴露自己的思维过程

德国教育家第斯多惠曾经说过:一个好的教师应该教人去发现真理.这就是说，教师讲题始终要坚持分析地讲,要充分暴露解题途径的寻找过程,“为什么要这样做”比“就这样做”更重要.而有的教师常常忽视这一点,解题时总是演示“成功”,思路、方法一想就很正确、很巧妙,从不展示“失败”,展示在思路和方法碰壁时怎么办,如何从有限次失败后得到正确的思路和方法,其结果只能是教师讲得精彩,学生听得轻松,但碰到条件稍加变化的问题便束手无策.日积月累,学生就不会独立地思考和克服困难,当然也不会有独立的解题能力.

案例4若a,b,c成等差数列，点P(-1,2)在直线l:ax+by+c=0上的射影为M，则点N(2,0)到点M的距离的最大值为.

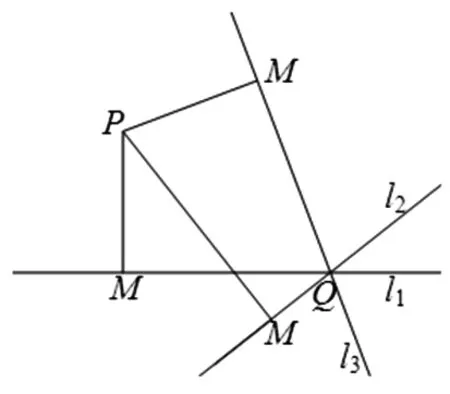
图1

思路二：如图1,尝试着画图，就会有下面的猜想：如果直线l:ax+by+c=0过定点Q，则射影点M的轨迹就是“以PQ为直径的圆”.一旦这个猜想是正确的，那么问题就很好解决了.紧接着就开始研究直线l:ax+by+c=0是否过定点.利用2b=a+c，代入直线l方程，可得ax+by+2b-a=0，所以a(x-1)+b(y-2)=0，从而得出直线l恒过定点Q(1,2).故射影点M的轨迹就是“以PQ为直径的圆”，其方程为x2+(y-2)2=1.下面的问题就很容易就解决了.

学会从多角度思考问题(特别是从数、形两个大的方向).以形助数，数形结合——解题之美，美就美在画图之后，借助图形的直观，使人产生丰富的联想，有了解题的灵感，寻找到了解题的思路，从而使问题的解决进行的很顺利，达到了从“数”的角度思考所无法达到的高度.同时也体现了数学“猜想”之美，解决问题时的“特殊与一般”的辩证之美.

在寻求解题思路时,要让学生逐步学会怎样分析,怎样判断,怎样推理,怎样选择方法,怎样解决问题,注意展现:(1)解题的思维过程,使学生的思维与教师的思维产生共鸣,使教师的思维为学生的思维过渡到科学的思维架起桥梁,变传授过程为发现过程;(2)尝试探索发现的过程,把失败过程和失败到成功的过程暴露出来,从反思中使学生看到转变思维的方向、方式、方法和策略,缩小探索范围,尽快获得发现的成功,这在发展思维能力上无疑是一种很好的体验和进步.

4.善于应用数学思想方法指导解题

“思想方法”是数学的灵魂，数学思想是学生对数学规律更进一步的掌握和认识，它指导着学生分析问题、解决问题并具体地体现在解决数学问题的不同方法中，掌握好数学思想也就是掌握了数学的灵魂，比单纯的掌握数学知识用处更大.

案例6 已知关于x的方程x2+2alog2(x2+2)+a2-3=0有唯一解，则实数a的值为.

许多学生拿到题目一筹莫展，无从下手.如果你从函数的“两域四性”这个角度去仔细观察，不难发现函数f(x)=x2+2alog2(x2+2)+a2-3是R上的偶函数，由偶函数图象的对称性可知：若f(x)=x2+2alog2(x2+2)+a2-3有一个零点，则只能是x=0，那么问题就迎刃而解.

数学的学习不仅是指数学知识的获得与积累，更重要的是使个体形成良好的数学认知结构，形成有序的、起作用的、有着生长点和开放面的认知结构.数学思想方法就是一个很好的切入点：(1)强化数形结合意识，进行直观感知；(2)强化化归意识，分散难点，实现多题归一；(3)学会用函数观点看待方程与不等式问题，突出体现函数方程思想.

三、解题教学的反思

数学解题的基本思维模式：观察——联想——变换.在数学解题教学中，我们不仅需要关注这道题怎么解，还需关注这道题还有没有其他的解法.通过教师引导，学生尝试从不同角度、不同方向分析问题，从而得到不同的解法.这对开拓优化学生的解题思路、拓宽学生的视野、提升学生思维的灵活性有很好的帮助.当然，教师在讲解题目时一定要突出学生学习的主体性，提高课堂学生的参与度，让学生成为课堂的真正主人.好的解题教学除关注以上几个方面外，笔者认为还需兼顾以下几点：

1.突出数学思想方法的提炼

布鲁纳说过：掌握数学思想方法可使得数学更容易理解和更容易记忆,更重要的是领会基本思想和方法是通向迁移大道的“光明之路”.因此，解题过程中,教师应有目标、有计划地引导学生体会、提炼其隐含的数学思想、方法,使学生在接受知识的同时,受到数学思想方法的熏陶和启迪,这样才能把提高学生的能力落到实处.

2.尊重学生的思维选择

教学活动遵循内在规律,只有当一切外在事实(知识)通过教师的主导作用,最后被主体(学生)认识之后,这外在的东西才会为主体真正占有,这种转化只有在参与实践中才能体会并完成.

3.正确处理好通法与巧法的关系

所谓通法,就是在解决问题(通常是某类问题)中具有普遍意义的方法.这种方法通常是以基础知识为依据,以基本方法为技能,它的解法思想合乎一般的思维规律,其具体操作过程必须为全体学生所掌握.巧法,着眼于提高.巧法的灵魂在于“巧”,即在于它整体地把握问题,灵活地运用双基,巧妙地使用条件,是抽象、概括、发散、合情推理的产物.当然,作为教师必须认识到,巧法中的“关键一着”有不少不属于学习内容的主体,更有不少是一般学生不易掌握的,加之“巧”便意味着运用面相对过窄,影响面小,所以教学中教师必须立足通法,兼顾巧法.

4.重视对典型错误的辨析

笔者认为,教师有意识地给学生设置解题陷阱,让学生陷进去,把典型错误暴露出来,引导学生积极思考,探索出正确的解题途径,是消除错误、治根治本的有效方法.教学的理论与实践表明,处理学生的解题错误,有很强的艺术性,处理得好,可让学生从错误中悟出新意,感受到探究问题的乐趣,从中学到比原间题更深更广的内容,既增强防止错误的免疫力,又能发展学生的智力.

解题教学是一门科学,也是一门艺术.“解题活动是学生在数学学习中最具有独立性的创造性活动,它对发展学生的思维,培养学生的能力,促进学生良好品质结构方面具有重大的作用.