数形结合思想在小学数学教学中的渗透策略

张嘉慧

摘要：随着教育事业的不断进步与发展，教师和家长们已经认识到数学对学生们思维发展的重要意义，数形结合作为学生的一种非常关键的数学思维能力，能够有效地提升学生学习和理解数学的效果。为此，对数形结合思想进行简要的分析，并且针对现阶段小学数学教学的现状提出数形结合思想的应用策略，为学生提供一种重要的学习方法和数学思想。

关键词：小学数学;数形结合;渗透

数形结合思想主要是通过数字与形状之间的对应及它们之间的联系进行转化，并且通过数与形之间的互相转化来解决数学问题的一种思想方法。数形结合思想不仅能够帮助学生理解数学这门学科的学科特点，同时还可以让学生通过练习掌握学习函数及解析几何等较为抽象的知识的方法与手段，为学生的数学学习打下坚实的基础。小学阶段的学生正处于从形象思维向抽象思维过渡的一个阶段，这个阶段教师教学的重点就是让学生在形的帮助下能够理解数的概念和意义。在日常教学过程中，如何借助形的直观来帮助学生实现由形象思维向抽象逻辑思维的过渡，成为目前数学教师关注的一个重点问题。

一、数形结合思想概述

数与形是数学知识体系的重要内容，在研究数量关系的过程中，通常把抽象化的数字关系通过转化为具象化的空间图形来解决问题。在教学中，教师把图形等将抽象化的知识内容转变为学生易于理解的数学语言，能够确保学生更加形象直观地理解数学知识内容。教师在培养学生数形结合思想的过程中，应结合学生的思维特点，有意识地进行逻辑思维的培养和锻炼。数形结合思想对学生的逻辑思维能力提出了较高的要求，否则，数形结合思想在数学教学中的实际效果将无法得到有效的发挥。

二、小学数学教学现状分析

（一）关注的重点有所偏失

在传统教学思想的长期影响下，很多教师已经形成了成绩高于一切的思想，认为学生的学习成绩才是教学的重点，因此对于学生的思维与创新等其他方面能力的发展有所忽视。在这种思想的影响下，教师的传道授业也仅仅局限于学生的考试范围，加之课程时间的限制，对于一些考试范围外学生应当掌握的知识内容，教师则闭口不谈，或者是仅仅谈及皮毛，这样的教学方式使得学生的核心素养无法得到有效发展。成绩如果成为衡量学生的唯一手段，那么教师也会按照成绩的好坏来区别对待学生，这对于学生数学知识的学习及数学能力的培养都是十分不利的。长期以往，学生很容易对数学学习产生逆反心理，尤其是数学这门学科具有一定的抽象性与系统性，学生理解起来会有一定的困难，如果教师不能改变教学观念和教学方法，会使学生在学习过程中产生一定的心理压力，这也在一定程度上违背了教师教学的初衷。

（二）教学方法单一，学生缺乏自主学习能力

就小学数学而言，要想提升这门学科的教学效果，教师要与学生互相配合，通过有效的教学方法让学生能够自主地参与到学习过程中来。小学生刚刚步入校园，与中学生相比认知水平较低且思维能力的发展还不够均衡，在思考问题与做题的过程中常常会机械地去背诵知识点，而不会去主动学习知识点，因此导致整体的学习处于一个较为被动的状态。面对这种情况，教师需要及时对学生思维特点及对知识的接受能力进行观察，从而有效地结合学生的身心发展特征来创新教学方法，开展教学。数形结合作为一种十分有效的方法，能够很好地将一些数学学习过程中学生难以理解的抽象的知识以一种直观形象的方式呈现出来，不仅能够激发学生对数学的兴趣，同时也让学生更为有效地吸收数学知识，可谓一举两得。

三、数形结合思想在小学数学教学中的渗透策略

（一）借助感性图标，形象诠释概念教学

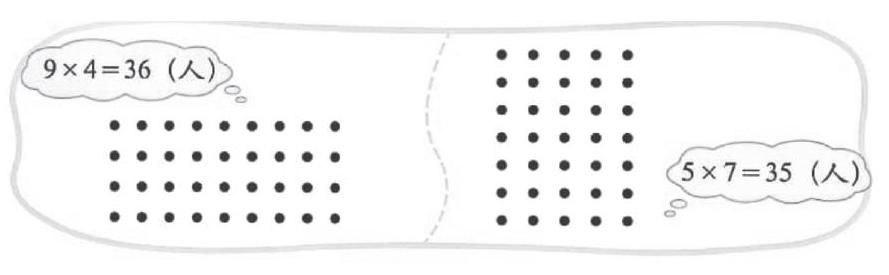
数学与其他学科的不同之处在于，其概念及相关的公式、原理需要在理解的基础进行记忆，仅死记硬背是无法真正理解其含义的，这说明数学具有极强的科学性。数学概念往往是十分精练和高度抽象的，它是人的大脑对一些现实中的数量关系及空间形式的一种本质反应。小学阶段是学生们形象思维茁壮成长的阶段，教师如果能够借助各式各样的材料及直观的教学方法将这些概念表现出来，就能够为在学生头脑中构建数学概念奠定良好的基础。如在学习“倍数与因数”时，为了让学生在头脑中有效地形成对“倍数”和“因数”的概念，教师可以让学生通过感受日常生活中排队时队列的相关现象，初步感知倍数和因数的概念。在学习这节课之前，学生尚未接触倍数与因数的概念，教师在课堂上出示学生校园生活中的排队图形，1班每排9人，共4排，2班每排5人，共7排。学生自主观察队列图，教师引导学生分别列式计算出两个班的总人数：9（因数）×4（因数）=36（倍数）;5（因数）×7（因数）=35（倍数）。在观察图形和列式的过程中，学生切实感受到排（因数）、列（因数）和总人数（倍数）的关系，以此引入倍数与因数的概念。通过对队形图的观察，学生能有效地理解倍数与因数的数学意义，能直观地感受到一般情况下倍数与因数在数量上的关系。现实生活中，很多事物在数量上可以通过倍数与因数来判断它们之间的关系。教师通过图形引入倍数与因数的概念和生活中的倍数与因数，学生可以更加深刻地理解倍数与因数的本质。

（二）借助图像表征，直观理解算理

算理作为数学中的一项重点教学内容，主要是引导学生理解计算方法的道理，其过程也是十分抽象的。教师可以借助图形的直观性特点进行教学，让学生更好地理解这部分的内容。如在学习“两位數乘以两位数”的过程中，学生对于两位数与两位数相乘的竖式及其建模的理解较为困难，对其计算方法的梳理也存在一定的困难。在这个过程中，教师需要借助几何直观来帮助学生对算理进行梳理，并且对其中抽象的概念如算理、算法等进行相应的总结。在学习这节课前，学生已经学习过了两位数乘以一位数。教师让学生根据顺序圈出不同的算式所表现出来的部分，引导学生在操作中理解拆分几个几和几十个几的过程，总结出其中的规律就是先分后和，之后让学生用竖式进行计算，实现由数到图再到数的转换，进而结合这几个重要的内容来梳理和厘清算理形成的过程。

最后，教师为学生呈现出四个乘法算式：2×4=8，1×2=2，1×4=4，1×1=1，同时在图上圈出表现的部分，让学生在动手实践中理解积的定义，从而学会数位对齐并深入理解其原理。在这个过程中，图片给算理提供了一个相应的载体，通过圈画，算理变得看得见、摸得着，有效地让学生掌握了相应的数学知识。

（三）借助几何直观，清楚凸显关系

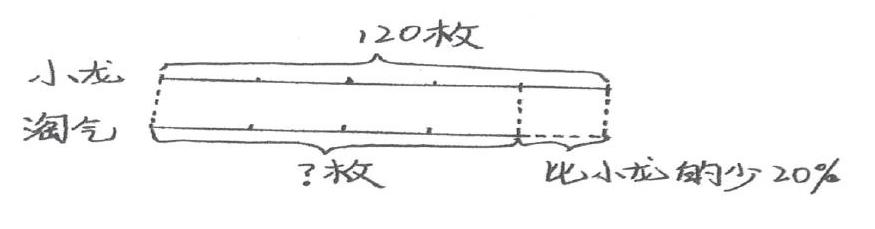
要想解决数学问题，首先要对问题进行有效的分析，让学生学会从不同的角度来观察问题。教师可以通过示意图、线段图及实物图等形式将数量关系直观地呈现在学生面前，降低问题的难度。如在学习“分数混合运算”和“百分数的应用”这两个单元的相关知识时，大量使用线段图能有效帮助学生分析和解决问题。如解决这道问题：小龙有邮票120枚，淘气的邮票数比小龙的少20%，淘气有多少枚邮票？在之前的学习里，学生初步掌握了“A的百分之几是多少”的相关知识和解决方法，但要解决这个问题，关键是理清小龙的邮票数和淘气的邮票数之间的数量关系。教师应引导学生通过画线段图来分别表示小龙的邮票数量和淘气的邮票数量，在画图的过程中适当提示：谁的邮票多？多多少？在画图的过程中，学生能逐步分析题目信息，并能使用直观的线段图找到列式的直通车。

学生借助数形结合思想有效地发现了问题的本质，有利于理清不同数量之间的关系，借助几何直观图形，量与率之间的对应关系也就一目了然，从而轻松地解决了问题。

参考文献：

[1]教育部.义务教育数学课程标准：2011 版[S].北京：北京师范大学出版社，2012.

[2]钟建林，林武.小学数学专题式教学导引[M].福州：福建人民出版社，2012.

（责任编辑：韩晓洁）