基于用电负荷的缺失数据插补方法研究

路 昂

(北京华电天仁电力控制技术有限公司，北京 海淀 100039)

0 引言

2015年，中共中央发布中发[2015]9号文[1]，文件制定了深化电力体制改革的总体思路、基本原则和重点任务[2]。我国的电力市场化交易体系形成了良好的开端，但对比成熟运行的电力市场，仍有许多方面需要改进[3]。电力市场发展表明，电力市场中发电企业与售电公司在各项业务环节中，需要较为准确的进行负荷预测作为数据分析与辅助决策的支撑。因此，提供准确的负荷预测等电力负荷数据分析是确保发电企业制定合理的发电计划，确保电力合理调配，节约电网控制成本[4]的关键一环。目前负荷预测的主要算法有深度学习方法[5]，BP神经网络法[6]，时间序列分析法[7]等。但是由于现实环境下负荷数据的采集容易受到随机因素的影响，以及负荷数据非线性程度高等特性，数据采集的完整率和准确率长期以来受到影响。另外由于统计时也会出现一定量的不良统计数据，其对电力系统负荷分析的精度产生了进一步的破坏[8]。因此对原始电力数据进行预处理，对缺失部分进行插补，得到完整数据集，对于电力数据分析来说具有重要的意义。

针对不良数据及缺失数据的补全，国内外学者开展了大量的研究工作。文献[9]将抽样调查中由于项目无回答所形成的缺失数据作为重点，从矩阵运算的角度分析了该缺失数据带来的危害，并对单一插补与多重插补方法的效率进行了研究与比较。文献[10]为提高数据插值的性能，提出了一种基于反向传播人工神经网络算子的鲁棒数据插值方法，与传统的反距离加权插值方法相比，该插值方法误差较小。文献[11]提出了缺失数据下联合均值与方差模型,在随机缺失情况下研究了3种插补方法对于模型的参数估计，并进行了插补结果的分析比较。

本文根据拟合曲线特征对用户电力负荷曲线进行分类并随机生成缺失值，用多种插补方法补全缺失数据，通过均方误差(mean square error，MSE)值比较并分析了不同插补方法对于不同类别用户的插补结果，对不同方法的准确性和适用性进行了验证，提高了插补效率。

1 数据插补原理

合理地补全缺失数据可以提高数据的质量，高质量的数据可以体现出数据集的整体特征以及数据个体信息。在进行数据分析之前，以最大程度恢复、补全缺失数据可以提高数据分析的准确性，对于数据的深度挖掘分析具有重要的意义。

为了补全缺失数据，延伸出很多种数据插补方法，但不同插补方法的中心思想都是用合理的数值来替代原始数据的缺失部分，以得到完整数据集。数据插补方法可分为单一插补和多重插补两大类。

本文首先描述了数据缺失机制，以及现有的缺失数据处理方法原理及其各自的优缺点；其次选取了6个典型的工商业用户，将6个用户按照负荷曲线特征分为两类；然后随机生成了每个用户10% 缺失率下的不完整数据集，并选取了适合本文样本数据的均值插补、回归插补和期望最大化(expectation maximization，EM)插补方法分别对缺失数据部分进行插补；最后，将插补后得到的数据集与原数据集进行对比，计算MSE值并对不同插补方法效果进行分析。

2 数据插补方法

本节首先介绍了数据的缺失机制，然后描述了不同类别的插补方法原理。

2.1 数据的缺失机制

数据的缺失机制分为3种情况：完全随机缺失、随机缺失和非随机缺失机制[12-13]。其中，完全随机缺失机制下，缺失值可以忽略，在图1中对应删除法。

图1 插补方法选择流程图Fig.1 Flow chart of interpolation method selection

记数据矩阵X中，Xobs为观测到的数据，Xmis为缺失数据。记矩阵R与矩阵X维度相同，R中的元素与X中的元素一一对应，且表示X中的元素是否缺失。R中的元素等于1表示X中的元素可以观测，R中的元素等于0表示X中的元素缺失。ξ为缺失机制相关参数。

1) 完全随机缺失：

P(R|Xobs，Xmis，ξ)=P(R|ξ)

(1)

2) 随机缺失：

P(R|Xobs，Xmis，ξ)=P(R|Xobs，ξ)

(2)

3) 非随机缺失：

P(R|Xobs，Xmis，ξ)结果不确定

(3)

2.2 现有的缺失数据处理方法

2.2.1 单一插补法

单一插补法是指通过对待插补数据集的非缺失部分进行数据挖掘，得到合适的代替值，并插补至缺失值位置的方法，主要包括以下几种。

1) 均值插补法。

均值插补的原理是用待插补数据集的所有非缺失部分的均值替代每个缺失值，从而得到完整的数据集。该方法过程简单，应用最为广泛[14]。

(4)

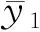
使用均值插补时，插补后的总体均值估计如下：

(5)

由于均值插补法利用一个相同的值来替代缺失数据，会使数据结构呈尖峰态，因此该方法会不同程度地改变原数据分布。

2) 回归插补法。

(6)

则采用回归法得到的插补值为

(7)

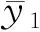
插补后，目标变量的总体均值估计为

(8)

回归插补法通过对目标插补值与其他数据之间的内在联系进行挖掘，建立回归模型得到目标插补值。该方法需要构造和评估回归模型，各属性间的回归关系越显著，插补准确度越高。

3) EM插补法。

EM插补法包括以下2个步骤。

E步：根据样本集数据，以及上一次迭代得到的参数估计θ(n)，对数似然函数的条件期望为

(9)

式中：Y为样本数据；Z为对应的隐变量数据。

M步：将Q极大化，反推新的参数估计值θ并用于下步的迭代：

(10)

不断迭代以上两步，直到计算得到的估计参数的差值|θ(n+1)-θ(n)|充分小停止。经过迭代，得到最终参数估计值θ与相应的完整数据集。EM算法应用较为广泛，很多文献也对该方法进行了扩展研究。

4) 热卡插补法。

热卡插补法步骤为：对于一个包含缺失值的变量，利用数据库中与它最相似的无缺失的数据单元的值对其进行插补，在等概率抽样情况下，总体均值估计量为

(11)

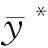
(12)

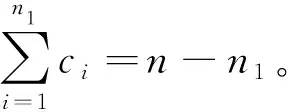
热卡插补法计算过程较慢，耗时较长，且容易使回归方程的误差增大，因此现阶段应用不太广泛。

2.2.2 多重插补法

多重插补法的典型代表为马尔科夫链蒙特卡洛(Markov chain Monte carlo，MCMC)法。多重插补过程中，MCMC法利用蒙特卡罗模拟实现马尔科夫过程，抽样过程随模拟进程的改变而改变，通过马尔科夫链实现缺失数据和参数分布收敛以模拟分布，实现动态模拟。

3 实验与结果分析

本文选取典型的工商业用户，生成用电负荷曲线，利用均值插补、回归插补和EM插补方法补全缺失数据。插补过程使用Matlab、SPSS软件，且在1.6 GHz、8 GB内存的笔记本电脑上运行。本文提出的对于不同类别用电负荷曲线进行数据插补的实验流程图如图2所示。

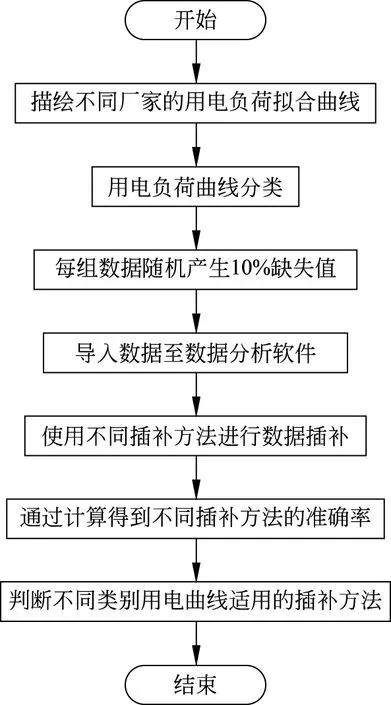
图2 实验流程图Fig.2 Experimental flow chart

3.1 原始数据及拟合曲线

选取6个典型的工商业用户，分别是广东四会互感器厂有限公司、中国电信股份有限公司汕尾分公司、紫金县石王水泥有限公司、广东吉荣电梯有限公司、汕头经济特区和兴音像有限公司和金钰(清远)卫生纸有限公司。各个用户的用电负荷数据以一天24个点，即每小时一次进行采样，选取2019年1月份16～20号5天的用电负荷数据(见表1—3)，并用MATLAB拟合生成回归曲线。

图3、图4为广东四会互感器厂有限公司、中国电信股份有限公司汕尾分公司2019年1月份16～20号全部原始负荷数据对应的拟合曲线。

表1 广东四会互感器厂有限公司、中国电信股份有限公司汕尾分公司部分原始数据Table 1 Partial original data of Guangdong Sihui Transformer Factory Co., Ltd. and Shanwei branch of China Telecom Co., Ltd.

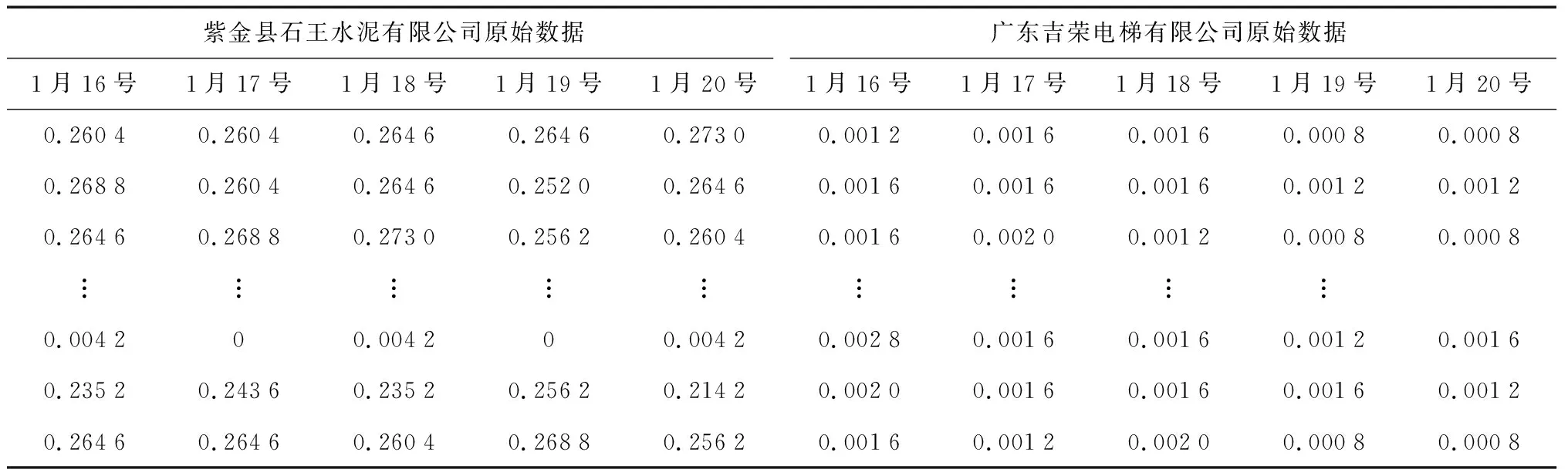
表2 紫金县石王水泥有限公司、广东吉荣电梯有限公司部分原始数据Table 2 Partial original data of Zijin Shiwang Cement Co., Ltd. and Guangdong Jirong Elevator Co., Ltd.

表3 汕头经济特区和兴音像有限公司、金钰(清远)卫生纸有限公司部分原始数据Table 3 Partial original data of Shantou Special Economic Zone Hexing Audio and Video Co., Ltd. and Jinyu (Qingyuan) Toilet Paper Co., Ltd.

图5、图6为紫金县石王水泥有限公司、广东吉荣电梯有限公司2019年1月份16～20号全部原始负荷数据对应的拟合曲线。

图7、图8为汕头经济特区和兴音像有限公司、金钰(清远)卫生纸有限公司2019年1月份16～20号全部原始负荷数据对应的拟合曲线。

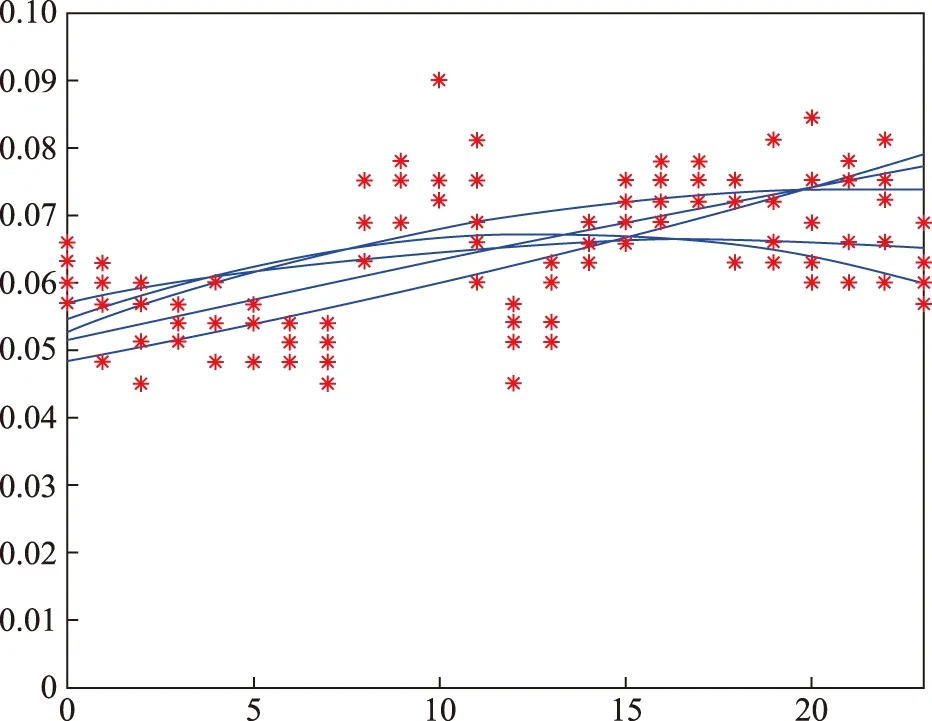
图3 广东四会互感器厂有限公司负荷拟合曲线Fig.3 Load fitting curve of Guangdong Sihui Transformer Factory Co., Ltd.

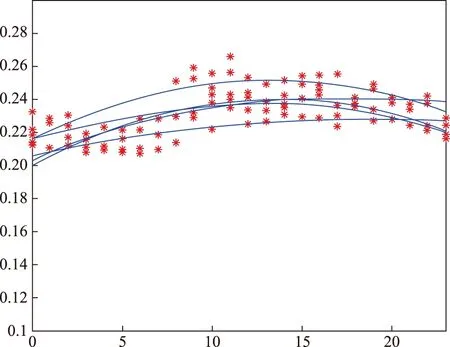
图4 中国电信股份有限公司汕尾分公司负荷拟合曲线Fig.4 Load fitting curve of Shanwei branch of China Telecom Co., Ltd.

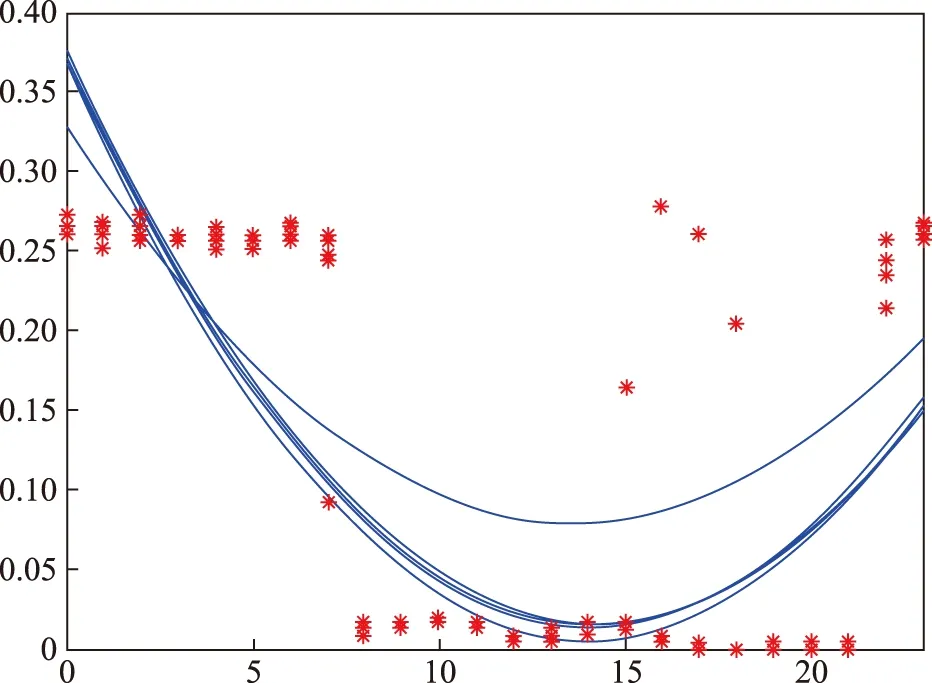
图5 紫金县石王水泥有限公司负荷拟合曲线Fig.5 Load fitting curve of Zijin Shiwang Cement Co., Ltd.

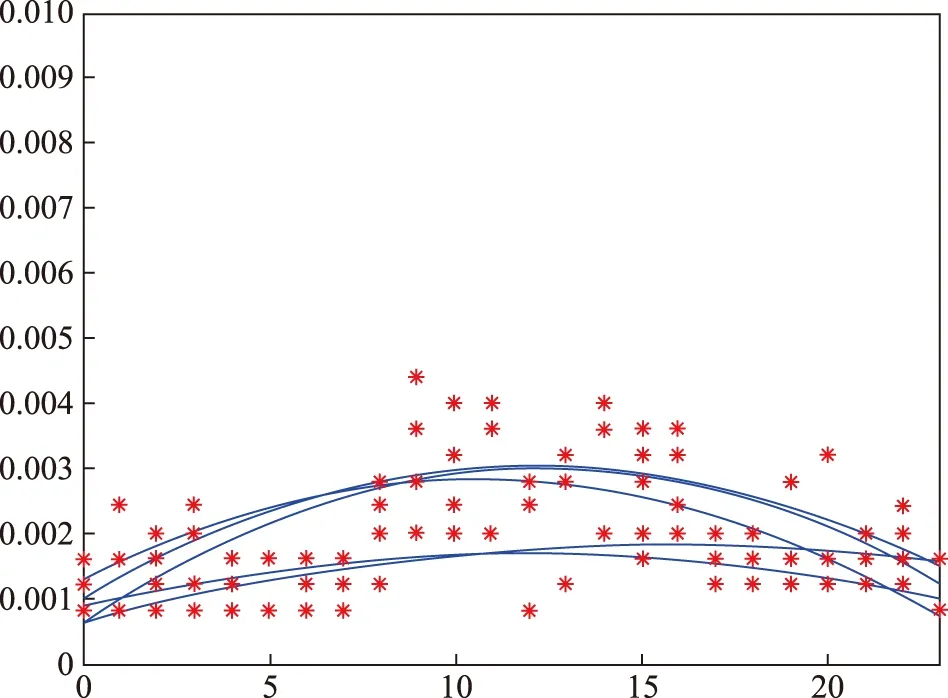
图6 广东吉荣电梯有限公司负荷拟合曲线Fig.6 Load fitting curve of Guangdong Jirong Elevator Co., Ltd.

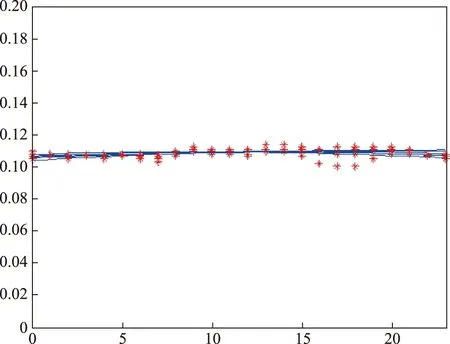
图7 汕头经济特区和兴音像有限公司负荷拟合曲线Fig.7 Load fitting curve of Shantou Special Economic Zone Hexing Audio Visual Co., Ltd.

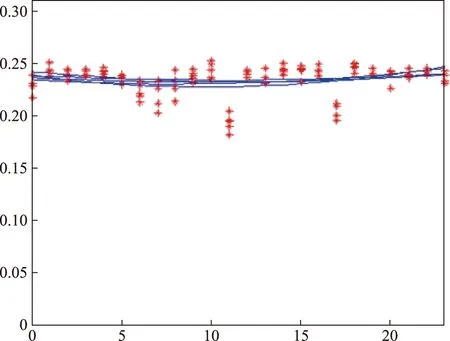
图8 金钰(清远)卫生纸有限公司负荷拟合曲线Fig.8 Load fitting curve of Jinyu (Qingyuan) Toilet Paper Co., Ltd.

为了验证不同插补方法的准确程度，首先对上述完整数据集进行处理，生成在10%缺失率下，含有随机缺失数据的不完整数据集。然后分别选择均值插补、回归插补、EM插补3种方法对各个不完整数据集进行数据插补工作，获得完整数据后，对比插补后数据集与原始数据集情况，通过计算MSE判断插补效果。

3.2 缺失数据及插补结果

进行缺失数据插补后，本文评价插补精确度采用的指标为MSE值。MSE是预测数据值与原始数据值之差平方的期望值，可以作为判断数据变化程度的评价指标。MSE的值越小，说明预测模型精确度越高。其表达式为

(13)

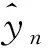
按照本文的实验方法，根据公式(13)可以得到6组实验中每一次数据插补的准确度，结果见表4。

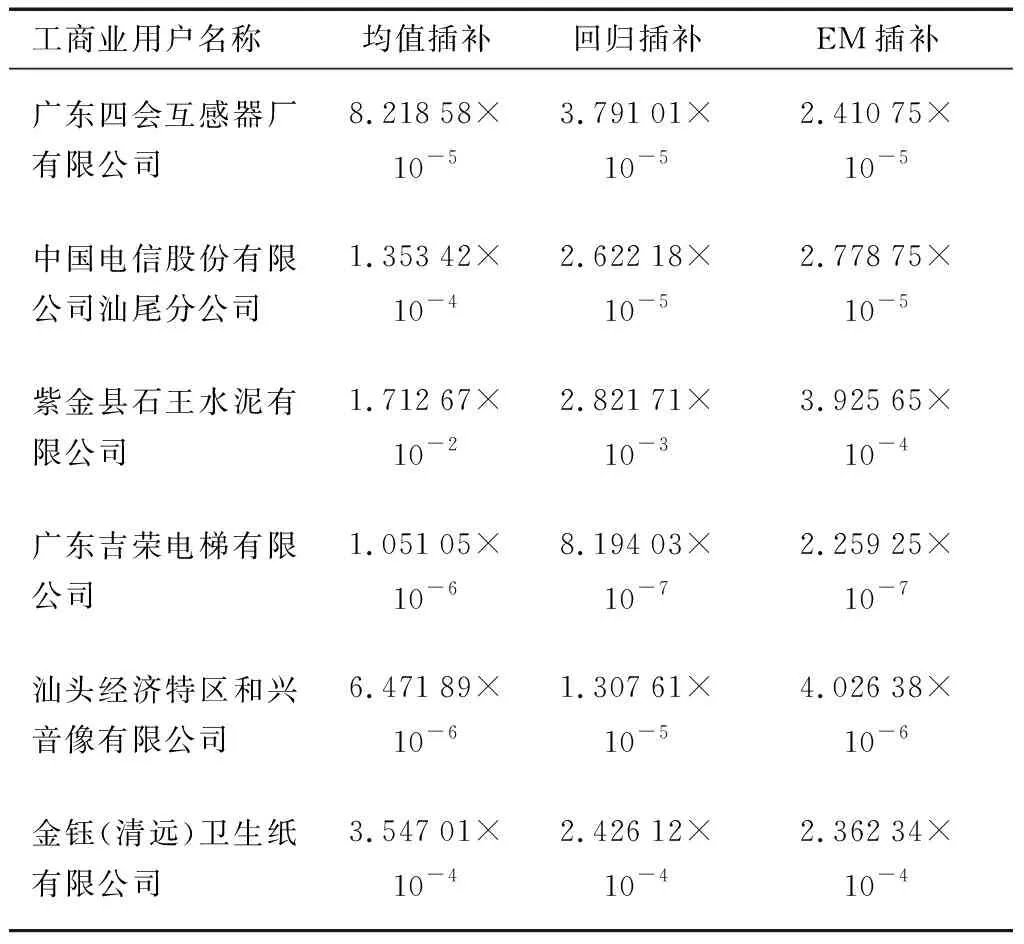
表4 不同插补方法的MSE值Table 4 MSE values of different interpolation methods

3.3 插补结果分析

按照拟合曲线特征，将6家工商业用户负荷曲线分为2类：

1) 类别1：变化幅度小，负荷曲线趋近于直线。包括广东四会互感器厂有限公司、汕头经济特区和兴音像有限公司、金钰(清远)卫生纸有限公司。

2) 类别2：变化幅度大，负荷曲线为有拐点的曲线。包括中国电信股份有限公司汕尾分公司、紫金县石王水泥有限公司、广东吉荣电梯有限公司。

对2类工商业用户负荷曲线的均值插补、回归插补和EM插补结果分别求均值，结果见表5。

表5 不同插补方法MSE平均值Table 5 MSE average value of different interpolation methods

通过对表4、5的分析可知，2种类别的MSE值从小到大排列均为EM插补、回归插补、均值插补，其中EM插补的MSE值最小，说明插补结果最接近原始数据；对于变化幅度小，负荷曲线趋近于直线的类别，回归插补、均值插补和EM插补的MSE值属于同一数量级；对于变化幅度大，负荷曲线为有拐点的曲线，回归插补与EM插补的MSE值属于同一数量级，而均值插补的MSE值较大。

4 结论

3种数据插补方法中，对于变化幅度小、负荷曲线趋近于直线和变化幅度大、负荷曲线为有拐点的2种类别曲线，EM插补方法的MSE值均为最小，插补结果最为准确，说明对于本文中的不同负荷曲线，EM插补方法适用性和准确性最好；回归插补方法的适用性和准确性次之；均值插补方法对于文中2种类别曲线的插补准确性均为最差，特别是对于变化幅度大、负荷曲线为有拐点的曲线，均值插补方法的误差较大，不适宜使用。