响应倾向得分匹配插补法

杨贵军，孙玲莉，李 璐

(天津财经大学 中国经济统计研究中心，天津300222)

一、引 言

在统计数据收集过程中，无回答总是不可避免。无回答直接影响数据分析结果的可靠性，一直是统计学、医学、生物学等领域研究和应用的热点［1］15－17［2］161－210［3］24－40［4－6］。插 补 法 通 过 特 定 算 法或模型给出无回答的插补值，是处理无回答问题的常用方法之一［7］47－67［8］。根据插补值个数，插补法可分为单重插补法和多重插补法。单重插补法仅给出无回答的一个插补值。多重插补法可以给出无回答的多个插补值，进而给出插补值的精度描述［1］。多重插补法的应用更为广泛。

根据插补原理，常用多重插补法主要分为三类。第一类是选用与无回答距离小的回答单元进行插补。例如，最近邻插补法依据回答单元与无回答单元之间的距离选择无回答插补值，常用的距离是欧氏距离。

倾向得分匹配插补法依据倾向得分的距离选择无回答插补值［9－11］。第二类是利用变量相关性进行插补。例如，回归插补法利用回答单元建立响应变量与解释变量之间的回归模型，根据回归模型得到无回答的插补值。Rubin最早提出线性回归多重插补法，Little和Rubin、Stef van Buuren将其扩展得到贝叶斯线性回归多重插补法、自助线性回归多重插补法［1］74－81［3］24－40［12］57－63。预测 均 值 匹 配 多 重 插 补 法(PMM)也属于回归插补法［13－14］［15］147－162。第三类是依据无回答的统计性质进行插补，例如，DA多重插补法［16－17］、EM 多重插补法及 EMB 多重插补法等［4，18］。其中，第二类多重插补法能保证变量之间的一致相关性，但对数据异常值较为敏感。第三类插补法往往迭代次数多，计算成本大。相比较，第一类插补法依据数据之间距离定义，应用领域更广。本文主要关注第一类插补法中的倾向得分匹配插补法。

倾向得分匹配插补法能处理实际经济问题中多种无回答情形。Paul和Rubin借助反事实提出倾向得分匹配(Propensity Score Matching)，利用Logistic模型平衡处理组与控制组的倾向得分，有效地均衡解释变量的分布［9］。若处理组和控制组不同个体之间的倾向得分相同或近似相等，则认为个体匹配。将倾向得分匹配法的思想用于无回答问题，称为倾向得分匹配插补法。无回答单元视为处理组，回答单元视为控制组。若无回答单元与回答单元之间的倾向得分相同或相近，对应的回答单元作为无回答单元的插补值。但倾向得分匹配插补法存在某些局限。一是倾向得分匹配插补法依赖于数据是否为无回答建立倾向得分模型。然而，实际问题中无回答往往是完全随机无回答或随机无回答。二是Logistic回归模型对无回答和回答的样本比例较为敏感。无回答的样本量较少或与回答样本量的差异大往往会导致Logistic回归模型拟合程度低，显著降低插补值的可信度。

基于上述讨论，利用倾向得分匹配插补法的思想，本文提出响应倾向得分匹配插补法(Response Propensity Score Matching Imputation)。响应倾向得分匹配插补法将回答单元的响应变量值的秩变换作为响应变量，与其他解释变量构建Logistic模型，作为响应倾向得分模型。将无回答单元和回答单元的解释变量带入模型分别得到无回答单元和回答单元的响应倾向得分。与无回答响应倾向得分差值小的回答单元，称为无回答单元的匹配，用于无回答的插补值。响应倾向得分匹配插补法保留了倾向得分匹配插补法的优良性，并且克服了无回答和回答的样本量差异影响，有效改善模型的拟合效果，提高插补值的可信度。

二、响应倾向得分匹配插补法

倾向得分匹配的思想最早是由 Paul和Rubin提出，用于解决因果推断中的处理组与控制组的匹配问题［9］。个体是否接受处理为二分类变量，与解释变量建立得分模型，依据倾向得分进行处理组和控制组的个体匹配。Little将倾向得分匹配思想应用于无回答，引入了倾向得分匹配插补法(Propensity Score Matching Imputation)［10］。现有文献将无回答和回答分别视为处理组和控制组，按是否回答设定示性变量作为响应变量，建立得分模型，若无回答单元与回答单元的得分相同或相近，认为无回答单元与回答单元匹配，用回答单元的响应值作为无回答单元的插补值［11，19］。一方面，这类倾向得分匹配插补法是按个体是否为无回答单元设定示性变量，但这与实际问题并不相符，实际中无回答单元往往是完全随机或随机无回答。另一方面，倾向得分模型对无回答和回答的样本量较为敏感。当无回答的样本量较少或与回答样本量的差异大，都会导致模型无法收敛，影响拟合模型的可信度和插补效果。

本文引入响应倾向得分匹配插补法。基本思想是将回答单元响应变量观测值依照从小到大的顺序排列，计算个体的秩，对秩变换为0至1区间内的数值，再与解释变量建立响应倾向得分模型。利用拟合的响应倾向得分模型，分别计算无回答组和回答组的单元响应倾向得分。考虑无回答组和回答组的响应倾向得分，将与无回答单元响应倾向得分差异小的回答单元作为无回答的匹配，对应的响应变量观测值作为无回答的插补值。相比于倾向得分匹配插补法，响应倾向得分匹配插补法的主要创新有两点，一是对响应变量观测值进行秩变换，二是建立秩变换与解释变量之间的倾向得分模型。引入秩变换是保证响应变量观测值的大小不发生错序，并使得响应变量观测值变换在0至1区间，改进倾向得分模型拟合效果，便于无回答组与回答组的个体匹配。响应倾向得分匹配插补法既不受无回答组和回答组的样本量差异大小影响，又保留了倾向得分匹配法的优良性。

假定响应变量为Y={Ymis，Yobs}，Ymis表示无回答单元的响应变量，Yobs表示回答单元的响应变量。无回答的样本量记为nmis，回答单元样本量记为nobs，n=nmis+nobs为总样本量。X={Xmis，Xobs} 表示 Y={Ymis，Yobs}对应的解释变量。假定解释变量不存在无回答，仅响应变量存在无回答。回答单元数据记为{X0，i，y0，i}(i=1，2，…，nobs)，无回答单元数据记为{X1，j，y1，j}(j=1，2，…，nmis)。响应倾向得分匹配插补法的具体步骤如下:

建立响应倾向得分模型。将回答单元响应变量值 y0，i(i=1，2，…，nobs) 按从小到大的顺序排列，记为 y0，1'，y0，2'，…，y0，n'obs，计算每个观测值的秩，分别记为 R0，i(i=1，2，…，nobs)。对秩进行变换，即:

利 用 h(X0，i) 与 解 释 变 量 X0，i= (x0，i1，x0，i2，…，x0，ik)'(i=1，2，…，nobs) 建立响应倾向得分模型。本文选择Logistic回归模型作为响应倾向得分模型，将h(X0，i) 作 为 被 解 释 变 量，X0，i= (x0，1，x0，2，…，x0，nobs)'作为解释变量，建立如下模型:

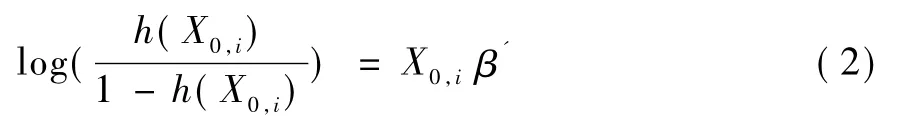
其中，β =(β1，β2，…，βk)'为模型系数，其估计值为拟合响应倾向得分模型为:

插补步。将无回答单元的解释变量 X1，j代入拟合模型(3)，得到无回答单元的响应倾向得分值(X1，j)(j=1，2，…，nmis)。计算无回答单元响应倾向得分值与回答单元响应倾向得分值的差值:

在回答组中，选择与无回答单元 j∈ {1，2，…，nmis}的响应倾向得分差值小的回答单元i∈{1，2，…，nobs}进行匹配。对于无回答单元 j，与回答单元的响应倾向得分差值满足:

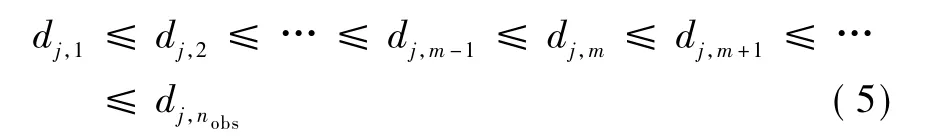
取前m个对应的回答单元响应变量值作为无回答单元响应值的m重插补值。

响应倾向得分匹配插补法保留了倾向得分匹配法的优点。将多个解释变量的相关信息转化为一个响应倾向得分值，简化匹配过程。响应倾向得分基于最近距离进行匹配，降低了高维数据处理的复杂度，更合理利用了回答组与无回答组的共同属性，提高了计算效率。另外，响应倾向得分匹配插补法保证无回答的随机性，不需要增加回答组和无回答组样本量平衡等假定条件。

三、随机模拟研究

利用统计模拟方法，探讨响应倾向得分匹配插补法的统计性质。Rubin将无回答机制分为完全随机无回答机制(MACR)、随机无回答机制(MAR)和非随机无回答机制(MNAR)［3］24－40。在非随机无回答机制下，常常不建议使用插补法。本文主要给出完全随机无回答机制和随机无回答机制下的模拟结果。无回答机制下的统计模拟细节请参考杨贵军等的研究［4］。本文选择的模型设定为:

其中，β0=1，β1=10，β2=1，β3=1，β4=2，ε为服从标准正态分布的随机误差项。X1，X2分别服从正态分布 N(1，4) 和 N(10，4);X3，X4分别服从二项分布 B(1，0．4) 和 B(1，0．5)。从解释变量 X1，X2，X3，X4的分布中随机产生100个随机数，根据模型(6)计算响应变量对应的100个观测值y1，y2，…，y100。这100个随机样本构成样本数据集。

本文主要选择了5%、10%、20% 共3种不同无回答率，4 种不同的插补重数，分别为 5、10、20、40，无回答机制分别为完全随机无回答机制和随机无回答机制。分别在无回答率、无回答机制与插补重数等多种组合情况下，采用响应倾向得分匹配插补法对无回答进行插补。在每种组合情况下，分别得到m组插补值，m组插补值与回答组数据合并为m组插补后的完整数据集。分别利用每组完整数据集，估计模型(6)的回归系数，得到m组回归系数估计值，记为。对m组回归系数分别取均值，即:3，4)作为模型(6)的系数估计值。

重复上述过程200次，得到200组系数估计值，计算回归系数估计的偏差和均方误差作为插补法优良性的评价指标。偏差是回归系数估计值与真值之差的平均数，均方误差为回归系数估计值与真值之差值平方的平均数。为了对比分析，这里也给出了采用基于欧式距离的最近邻插补法、倾向得分匹配插补法和回归插补法的模拟结果。结果显示在完全随机无回答机制下和随机无回答机制下，无回答率为10%的模拟结果介于无回答率为5%和20%的模拟结果之间。后文中仅给出无回答率为5%和20%的具体结论。

(一)完全随机无回答机制下回归系数估计量的偏差和均方误差

在完全随机无回答机制下，分别使用响应倾向得分匹配插补法、最近邻插补法、倾向得分插补法以及回归插补法分别对Y的无回答进行插补，并估计模型的回归系数。本节的最近邻插补法选用的是欧式距离。在插补重数、插补法和无回答率的组合下的回归系数估计偏差和均方误差见表1和表2。表1、表2依次对应无回答率5%、20% 的模拟结果。在表1和表2中，A、B、C、D依次表示响应倾向得分匹配插补法、最近邻插补法、倾向得分匹配插补法以及回归插补法。每行对应的插补重数相同。第3～7列依次给出了回归系数估计的偏差，第8～12列依次给出了回归系数估计值的均方误差。如表1中第1行数值0．074、－0．023、－0．005、－ 0．052、0．030依次为响应倾向得分匹配插补法且插补重数为5的的偏差，0．251、0．008、0．002、0．113、0．092依次为响应倾向得分匹配插补法且插补重数为5的的均方误差。

表1显示，插补重数对回归系数估计的偏差和均方误差都有影响。随着插补重数增加，响应倾向得分匹配插补法的回归系数估计偏差绝对值和均方误差都有增加趋势，其中常数项估计的偏差绝对值和均方误差增加幅度大，其他系数的偏差绝对值和均方误差增加幅度小。最近邻插补法的回归系数估计量的偏差绝对值和均方误差随着插补重数增加也呈现递增趋势，增加幅度明显大于基于响应倾向得分匹配插补法的结果。倾向得分匹配插补法的回归系数估计量的偏差绝对值和均方误差随着插补重数增加并没有呈现明显的递增趋势的偏差绝对值和的均方误差随着插补重数增加甚至呈现递减趋势。回归插补法得到的回归系数估计的偏差绝对值和均方误差随着插补重数增加呈现略微递减趋势。

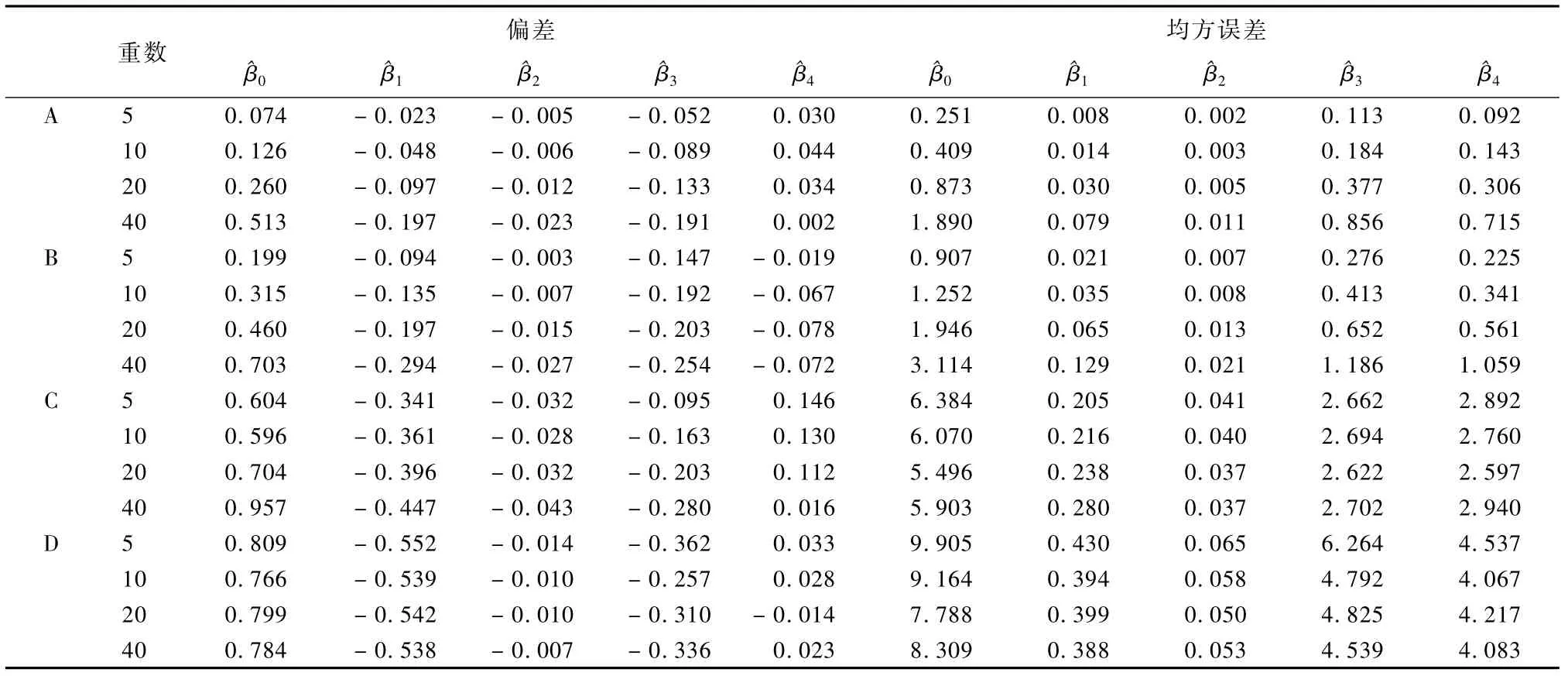
表1 完全随机无回答机制下无回答率为5%的模拟结果

表2 完全随机无回答机制下无回答率为20%的模拟结果

表1显示，不同插补法对系数估计量的偏差和均方误差的影响不同。相比较而言，响应倾向得分匹配插补法最优，相应的系数估计量的偏差绝对值和均方误差都较小。最近邻插补法的回归系数估计的偏差绝对值和均方误差也较小，但略大于响应倾向得分匹配插补法的结果。倾向得分匹配插补法和回归插补法的偏差绝对值和均方误差明显大于前两种方法。

表2给出了完全随机无回答机制下无回答率为20%的模拟结果。表2显示，插补重数对回归系数估计的偏差和均方误差都有影响。随着插补重数增加，响应倾向得分匹配插补法和最近邻插补法偏差绝对值和均方误差呈现递增趋势，其中增加幅度小的是响应倾向得分匹配插补法。倾向得分匹配插补法和回归插补法的偏差绝对值和均方误差随着插补重数增加呈现递减趋势，回归系数估计的均方误差要大于前两种插补法。表2显示，响应倾向得分匹配插补法系数估计的偏差绝对值和均方误差都相对较小，小于其他插补法。对比表1和表2可知，随着无回答率增加，采用四种插补法得到回归系数估计的偏差绝对值以及均方误差也往往增加。

在完全随机无回答机制下，响应倾向得分匹配插补法的回归系数估计的偏差绝对值和均方误差，随着插补重数增加呈现递增趋势，也随着无回答率增加而呈现递增趋势。

(二)随机无回答机制下回归系数估计量的偏差和均方误差

随机无回答机制的设定与解释变量有关，考虑分别依赖于连续变量X1，X2与离散变量X3，X4的随机无回答机制。变量X1，X2模拟结果规律相似，变量X3，X4的模拟结果规律相似，本节只给出依赖连续变量X1与离散变量X3的模拟结果。

1．依赖连续变量X1的随机无回答机制。表3和表4分别表示无回答率为5%、20% 时依赖连续变量X1的随机无回答机制下的模拟结果，结构同表1。

表3 依赖连续变量X1随机无回答机制下无回答率为5%的模拟结果

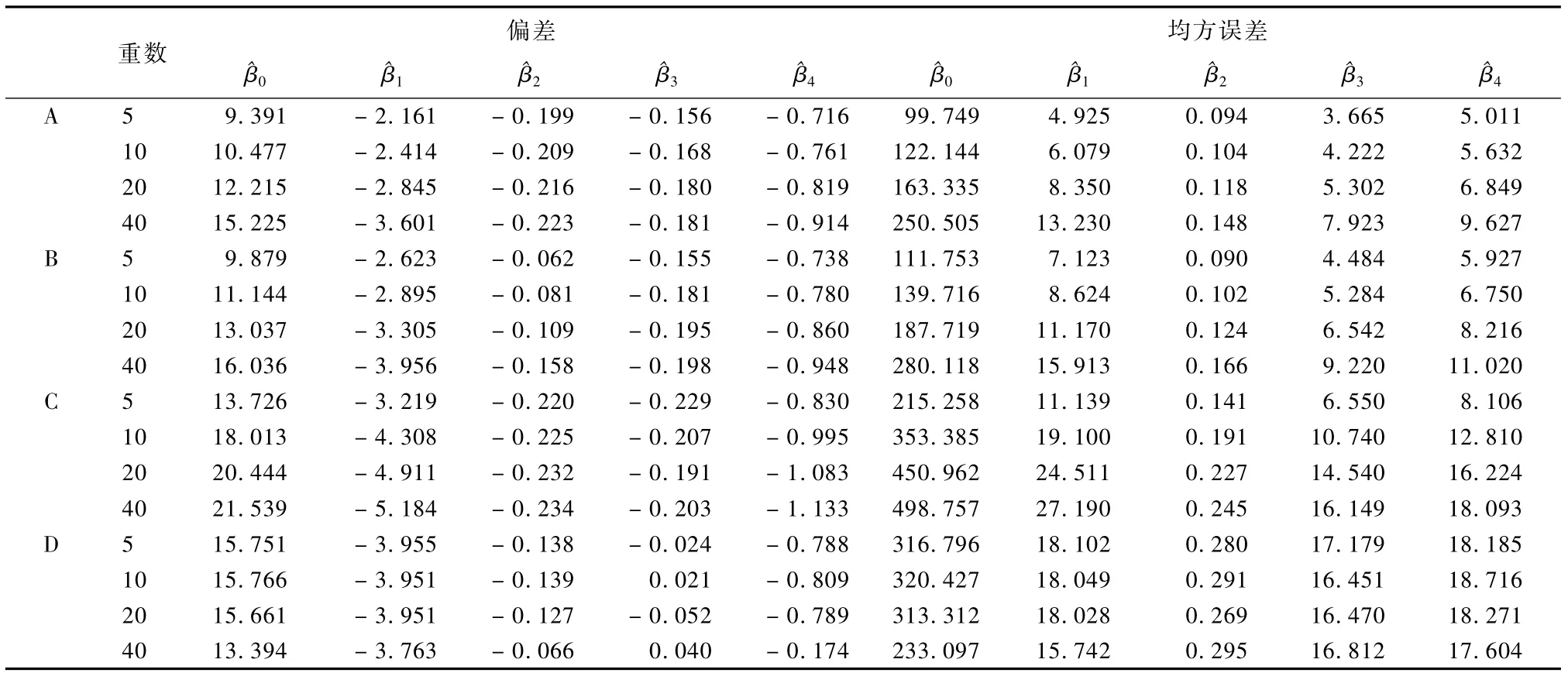
表4 依赖连续变量X1随机无回答机制下无回答率为20%的模拟结果

表3显示，在依赖连续变量X1的随机无回答机制下，插补重数对回归系数估计量的偏差和均方误差都有影响。随着插补重数增加，响应倾向得分匹配插补法回归系数估计偏差绝对值和均方误差都有增加趋势，常数项估计的偏差绝对值和均方误差增加幅度大，其他系数的偏差绝对值和均方误差增加幅度小。最近邻插补法的回归系数估计量的偏差绝对值和均方误差随着插补重数增加也呈现递增趋势，增加幅度明显大于基于响应倾向得分匹配插补法的结果。倾向得分匹配插补法的回归系数估计量均方误差随着插补重数增加呈现递增趋势，^β2、^β4的偏差绝对值随着插补重数增加甚至呈现递减趋势。回归插补法的回归系数估计的偏差绝对值和均方误差随着插补重数增加呈现略微递减趋势。

表3显示，在依赖连续变量X1的随机无回答机制下，不同插补法对系数估计量的偏差和均方误差的影响不同。相比较而言，响应倾向得分匹配插补法最优，相应的系数估计量的偏差绝对值和均方误差都较小。最近邻插补法的回归系数估计的偏差绝对值和均方误差也较小，但略大于响应倾向得分匹配插补法的结果。倾向得分匹配插补法和回归插补法的偏差绝对值和均方误差明显大于前两种方法。在几种插补法下，相对于其他回归系数，^β2的偏差绝对值和均方误差都最小，偏差绝对值小于0．05，均方误差都小于0．3。

表4为依赖连续变量X1随机无回答机制下无回答率为20%的模拟结果。表4显示，随着插补重数增加，响应倾向得分匹配插补法、最近邻插补法、倾向得分插补法的偏差绝对值和均方误差随着插补重数增加呈现递增趋势，其中增加幅度小的是响应倾向得分匹配插补法。回归插补法的偏差绝对值和均方误差随着插补重数增加呈现略微递减趋势，回归系数估计的均方误差要大于前三种插补法。表4显示，响应倾向得分匹配插补法系数估计的偏差绝对值和均方误差都相对较小，小于其他插补法。对比表3、表4可知，随着无回答率增加，采用四种插补法得到的回归系数估计的偏差绝对值和均方误差递增趋势显著。

对比完全随机无回答机制下的模拟结果，依赖连续变量X1随机无回答机制下，采用四种插补法得到的回归系数估计的偏差绝对值和均方误差的普遍大于完全随机无回答机制下的偏差绝对值和均方误差。

2．依赖离散变量X3的随机无回答机制。变量X3为一个二分类变量，参考Jonathan Kropko等人的研究成果中对分类变量的随机缺失机制模拟的方法［20］。首先利用Logistic函数将二分类变量转换为概率 π，对于每个 x3，i都有一个对应的概率 πi，再减去U(0，1)中的一个随机数di，得到了100个观察变量= πi－ di(i=1，2，…，100)。依据无回答率确定变量的分位数，将小于该分位数的观测 yi，x1i，x2i，x3i，x4i中yi设定为无回答。利用插补法对Y的无回答进行多重插补，再估计模型的回归系数。表5、表6分别表示无回答率为5%、20%时依赖离散变量X3的随机无回答机制下的模拟结果，结构同表1。

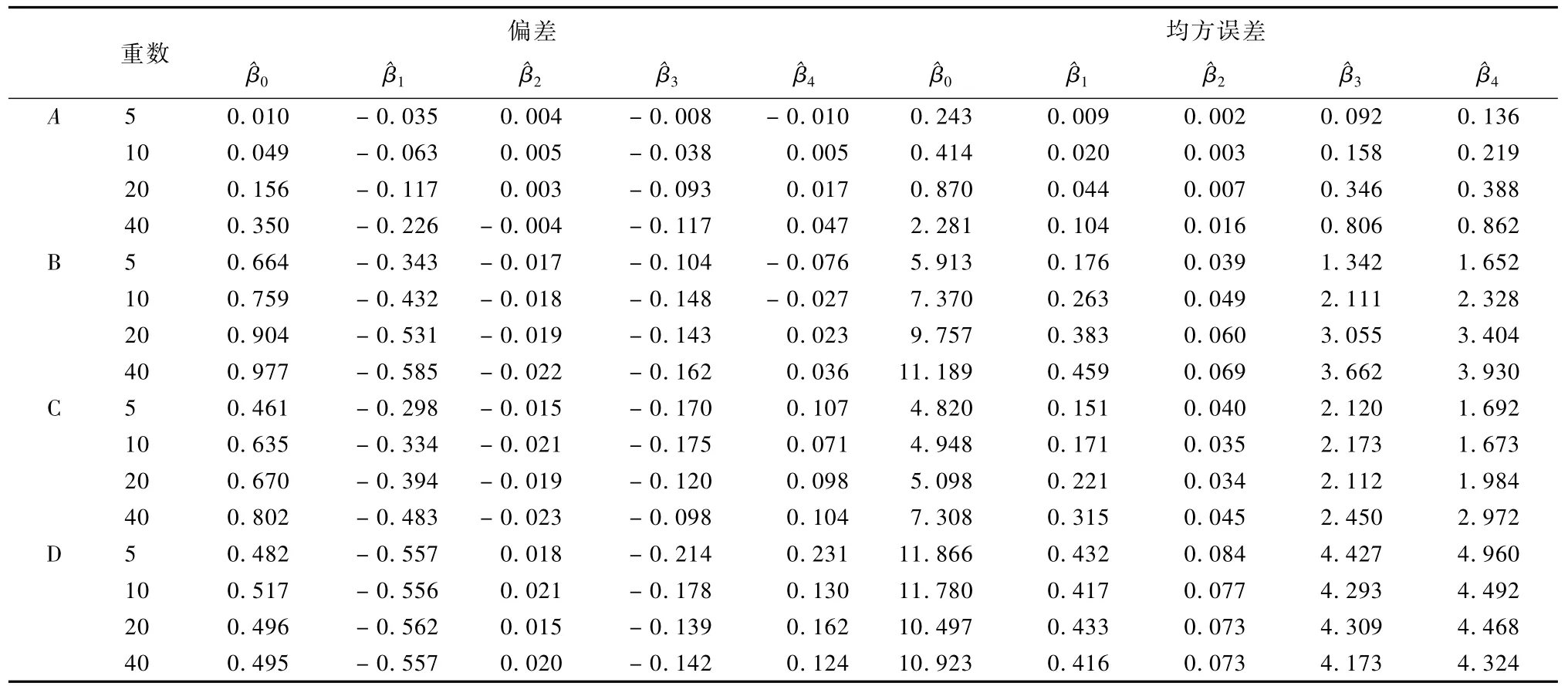
表5 依赖离散变量X3随机无回答机制下无回答率为5%的模拟结果

根据表5可知，在依赖离散变量X3的随机无回答机制下，插补重数对回归系数估计量的偏差和均方误差有影响。随着插补重数增加，响应倾向得分匹配插补法、最近邻插补法、倾向得分匹配插补法的回归系数估计偏差绝对值和均方误差都有增加趋势。最近邻插补法的回归系数估计量的偏差绝对值和均方误差的递增幅度明显大于基于响应倾向得分匹配插补法和倾向得分匹配插补法的结果。回归插补法得到回归系数估计的偏差绝对值和均方误差随着插补重数增加呈现略微递减趋势。

表5显示，在依赖离散变量X3的随机无回答机制下，不同插补法对回归系数估计量的偏差和均方误差影响不同。响应倾向得分匹配插补法效果最优，其对应回归系数估计量偏差绝对值和均方误差明显小于最近邻插补法、倾向得分匹配插补法和回归插补法的结果。倾向得分匹配插补法的偏差绝对值和均方误差小于最近邻插补法和回归插补法的结果。

表6为在依赖离散变量X3的随机无回答机制下无回答率为20%的模拟结果。表6显示，随着插补重数增加，响应倾向得分匹配插补法、最近邻插补法、倾向得分插补法的偏差绝对值和均方误差随着插补重数增加呈现递增趋势，其中增加幅度小的是响应倾向得分匹配插补法。回归插补法的偏差绝对值和均方误差随着插补重数增加呈现略微递减趋势，回归系数估计的均方误差要大于前三种插补法。表6显示，响应倾向得分匹配插补法的系数估计的偏差绝对值和均方误差都相对较小，小于其他插补法。对比表5、表6可知，随着无回答率增加，采用四种插补法得到的回归系数估计的偏差绝对值和均方误差递增趋势显著。

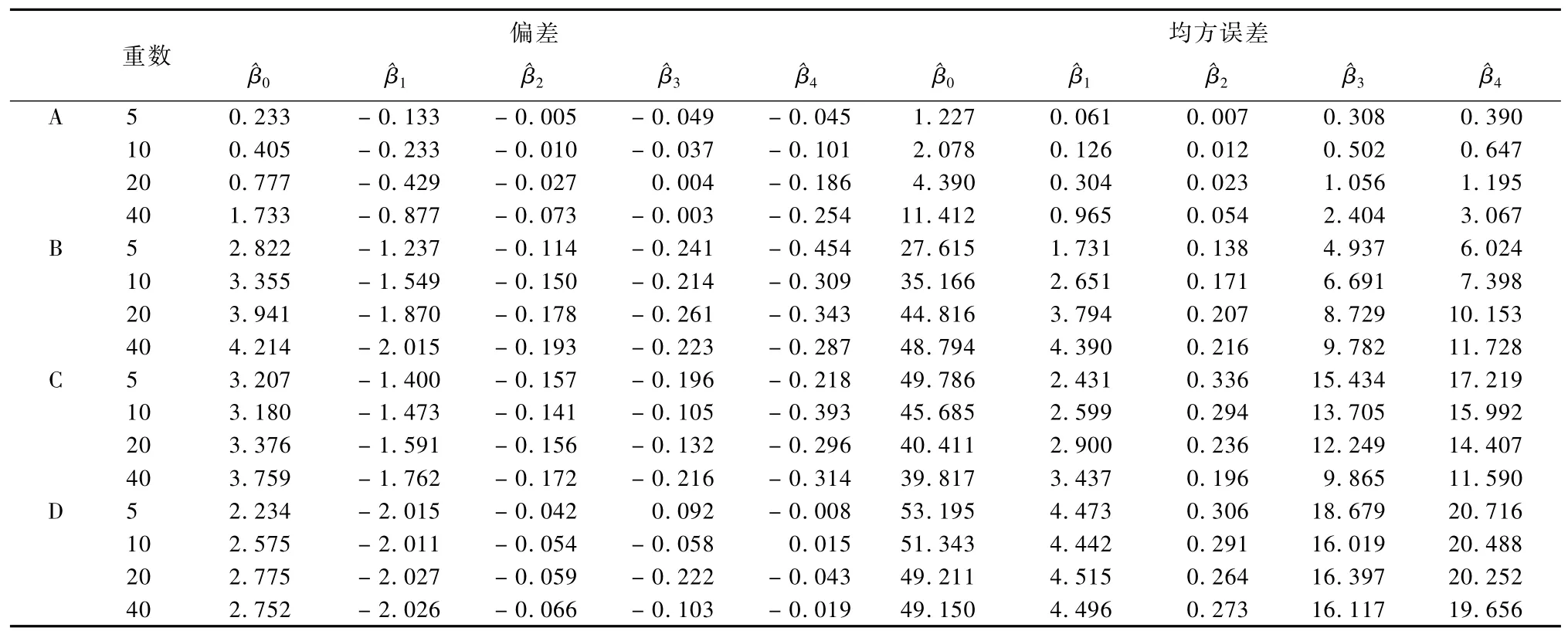
表6 依赖离散变量X3随机无回答机制下无回答率为20%的模拟结果

对比完全随机无回答机制下和依赖连续变量X1的模拟结果，依赖离散变量X3随机无回答机制下，采用四种插补法得到的回归系数估计的偏差绝对值和均方误差普遍大于完全随机无回答机制下的偏差绝对值和均方误差，但小于依赖连续变量X1随机无回答机制下偏差绝对值和均方误差。

综上所述，在完全随机无回答机制下和随机无回答机制下，响应倾向得分匹配插补法的插补效果明显优于最近邻插补法、倾向得分匹配插补法和回归插补法。随着插补重数增加，响应倾向得分匹配插补法的偏差绝对值和均方误差呈递增趋势。在实际使用响应倾向得分匹配插补法时，插补重数选择不宜过大，建议插补重数选择为5。

四、实证分析

本研究使用响应倾向得分匹配插补法分析Sparrows数据集［21］29－31①数据下载网址:http://highstat．com/index．php/a-beginner-s-guide-to-r。Sparrows数据集有 979 个样本观测值。本文选择6个变量分别是:Wingcrd(羽翼长度)、Sex(性别)、Tarsus(胫骨长度)、Head(头的尺寸)、Culmen(上嘴长度)、Wt(重量)。其中，性别中雌性表示为1，雄性表示为0。以Wingcrd为响应变量，其余变量为解释变量。为了描述羽翼长度，建立如下的线性模型:

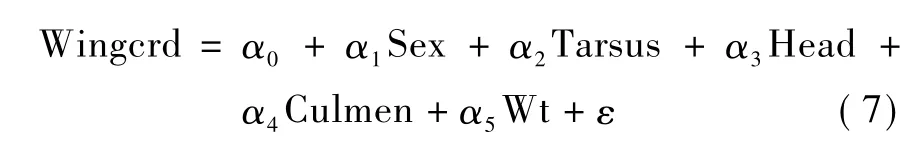
利用Sparrows数据集的数据拟合模型(7)，估计结果如表7第2、3行所示。表7的列分别对应模型系数，第2、3行分别表示系数估计值及其方差估计。在显著性水平0．005下，所有的系数估计都是显著的。模型整体拟合效果较好，R2=0．634。其中，系数α1的估计值2．206为正，说明雌性麻雀要比雄性麻雀的羽翼更长。α2和 α3的估计值为正，不超过0．3，说明麻雀的胫骨越长，头部越大，其羽翼更长。α4和 α5估计值为正，接近 0．4，说明麻雀的上嘴越长，重量越大，其羽翼更长。模型(7)的参数估计合理。

表7 Sparrows数据集的估计结果

针对Sparrows数据集，构造无回答，无回答率为5%(49/979≈0．05)。在完全随机无回答机制和随机无回答机制下，构造49个观测的响应变量Wingcrd为无回答。使用响应倾向得分匹配插补法，选择插补重数 m=5，依次得到参数 αk(k=0，1，…，5)的5个估计值，取5个估计值的平均数作为参数αk的估计值。插补后估计量的方差计算采用Rubin(1987)的公式:

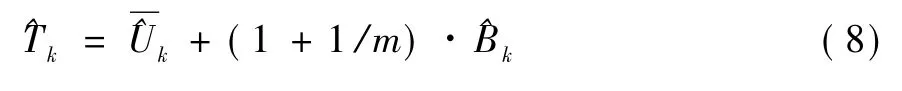
在完全随机无回答机制下，采用响应倾向得分匹配插补法的估计结果如表7第4和5行所示。其中，第4行是回归系数 αk(k=0，1，2，…，5) 的200个估计值的平均数，第5行是200个方差估计的平均数。首先，从参数估计值角度。表7显示，采用响应倾向得分匹配插补法的估计值平均数，与利用全部数据的参数估计值的差异小。相比较，最大的是常数项α0的估计值差值，为 0．082。对于参数 α3，两者差异为 0．005，对于参数 α1、α2、α4和 α5，两者差值小于等于 0．002。其次，从参数方差估计角度。在表7中，采用响应倾向得分匹配插补法的方差估计平均数略大于利用全部数据的参数方差估计，两者差异小。其中常数项α0的两者差异最大，为0．820。对于其他参数，两者差值不超过0．002。在完全随机无回答机制下，采用响应倾向得分匹配插补法，能够得到较好的模型系数。

在随机无回答机制下，分别考虑了无回答依赖于变量 Sex、Tarsus、Head、Culmen、Wt的情况。采用响应倾向得分匹配插补法的估计结果如表7第6至15行所示。在依赖于每个变量的估计结果中，第1行是回归系数 αk(k=0，1，2，…，5) 的200个估计值的平均数，第2行是200个方差估计的平均数。类似，先观察参数估计值。表7显示，采用响应倾向得分匹配插补法的估计值平均数，与利用全部数据的参数估计值的差异小。相比较，常数项α0的估计值差值最大。其中，依赖变量 Head的估计值差值为1．719，依赖其他变量的常数项的估计值差值均小于0．2。对于参数 α3和 α4，不超过 0．095。对于参数 α1、α2和α5，两者差异更小，不超过 0．05。再观察参数方差估计。在表7中，采用响应倾向得分匹配插补法的方差估计平均数略大于利用全部数据的参数方差估计，两者差值小。其中，对于常数项α0，两者差异最大，不超过0．7。对于其他参数，两者差值不超过0．002。在随机无回答机制下，采用响应倾向得分匹配插补法，能够较好估计模型系数。

五、结 论

在数据收集过程中，不可避免存在无回答。多重插补法是用于处理无回答的主要方法之一。本文引入了响应倾向得分匹配插补法。将回答单元响应变量观测值的秩进行变换，建立响应倾向得分模型。依据响应倾向得分模型分别得到回答单元和无回答单元的响应倾向得分，匹配无回答单元和回答单元的响应倾向得分确定无回答的插补值。响应倾向得分匹配插补法对无回答和回答单元的样本量差异大小无要求。相比于倾向得分匹配插补法，有效改善了模型拟合效果，提高插补的可靠性。

模拟结果显示，在完全随机无回答机制和随机无回答机制下，响应倾向得分匹配插补法优于最近邻插补法、倾向得分匹配插补法和回归插补法。在相同的无回答机制下，随着插补重数增加或随着无回答率增加，采用响应倾向得分匹配插补法的回归模型系数估计的偏差绝对值和均方误差呈递增趋势。利用Sparrows完整数据集的分析结果显示，在完全随机无回答机制和随机无回答机制下，使用响应倾向得分匹配插补法的回归系数估计值与使用完整数据集得到的估计值和方差估计的差异都较小。在实际应用响应倾向得分匹配插补法时，插补重数选择不宜过大，建议插补重数选择为5。