高寒高海拔地区风光互补热电联供系统多目标优化研究

2020-09-21檀丛青王志奇陈柳明谢宝琦

分布式能源 2020年4期

檀丛青，王志奇，陈柳明，赵斌，谢宝琦

(湘潭大学机械工程学院，湖南湘潭 411105)

0 引言

高寒高海拔地区居民地处偏远且居住点分散，极大地增加了电网供电和集中供暖的投资费用。因此，供电与供暖问题已成为制约高寒高海拔地区经济发展和居民生活水平提升的主要因素。高寒高海拔地区风能、太阳能等可再生能源丰富，然而单一风能发电或者光伏发电模式具有显著的波动性和间歇性[1-2]，难以提供稳定的电能和热能。太阳能和风能在时域和地域上都存在很强的互补性，将光伏发电和风力发电相结合能有效提升系统的稳定性[3-4]。因此，风光互补系统是解决高寒高海报地区供暖与供电问题的有效途径。

合理配置系统容量，是进一步提高风光互补热电联供系统可靠性与经济性的关键。为此，国内外学者对风光互补系统的容量配置开展了优化研究。如齐志远等[5]以系统发电成本为目标，采用改进和声搜索算法对系统配置进行优化。徐璋等[6]应用粒子群优化算法对风光互补系统的配置进行优化设计，有效降低了系统的总成本。此外，随着人们对环保问题的日益关注，唐浩等[7]以系统等效CO2排放量为目标，对容量配置进行了优化。然而，这些研究采用的都是单目标优化，仅考虑了系统的经济性或环保性。

实际工程中，风光互补系统具有多个方面的性能需求，如经济性、可靠性与环保性，单目标优化难以平衡不同需求之间的冲突。为此，一些学者应用多目标优化方法开展系统容量配置设计。如一些学者考虑系统的总成本和失负荷概率，对风光互补系统配置进行多目标优化设计，较好地平衡了系统的经济性与可靠性[8-10]。杨冬等考虑输出功率波动性、设备利用率与清洁能源浪费率等性能指标，从系统可靠性与经济性角度对容量配置进行优化[11]。此外，Rodolfo等[12]以系统供能成本与等效CO2排放量为目标，对风光互补系统进行优化，有效提升了系统的综合性能。然而，这些研究主要针对风光互补发电系统进行多目标优化，并未考虑用户的供暖需求。同时，这些研究一般采用2个优化目标，并没有综合考虑系统的经济性、可靠性与环保性。

为此，本文以风光互补热电联供系统为研究对象，建立该系统主要部件的数学模型，并以系统总投资成本、负荷缺失率与等效CO2减排量为目标，构建热电联供系统的多目标优化模型；在此基础上，以西藏那区为例，利用NASG-II算法对系统配置进行优化设计，获得符合气象条件的最优配置。

1 风光互补热电联供系统数学模型

1.1 系统简介

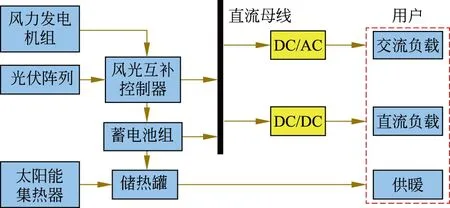
图1 风光互补热电联供系统布置图Fig.1 Sketch of wind-solar hybrid co-generation system

风光互补热电联供系统由风力发电机组，光伏电池阵列、储能单元、控制系统和逆变系统、集热器、储热罐等部件组成，其布置如图1所示。相比风光互补发电系统，该系统增加了供暖功能，且供电系统会作用于供暖系统，增大了系统容量配置的难度。

在该风光互补系统中，风力发电机与光伏阵列产生的电能经控制器后，向用户输出电能；当产生电能高于负载量时，向蓄电池充电；太阳能空气集热器吸收太阳能，并利用换热器将热量传递给液体媒介，储存在储热罐中，然后再向建筑供暖；当负载耗电量大于发电量时，蓄电池向负载供电；当储热罐中的能量低于建筑热负荷时，蓄电池给储热罐中的加热器提供电能。

1.2 风光互补系统模型

1) 风机数学模型。

风机的功率和风速满足如下函数关系[13]：

(1)

式中：PW(t)为风机在该时刻的实际输出功率，W；Pr为风机的额定输出功率，W；vr表示额定风速，m/s；vi为风机切入风速，m/s；vo为风机切出风速，m/s。本文采用FD2.7-1.0/12风力发电机，其额定功率为1 000 W，额定风速、切入风速与切出风速分别为10 m/s，3 m/s与14 m/s。

2) 太阳能光伏阵列数学模型。

考虑光照强度与电池自身温度的影响，太阳能光伏阵列的输出功率[5]为：

式中：PPV,STC为标准测试条件下光伏发电单元的最大测试功率，W；G为太阳光照强度，取1 000 W/m2；t为时间，h；T为温度，℃；k为功率温度系数，取-0.45%；TNOCT为组件额定工作温度，℃；下标STC，air分别表示测试条件与环境。本文选用STP265-20光伏板，其峰值功率为265 W。

3) 太阳能集热器模型。

考虑辐射、对流等热损失，根据热平衡关系可得循环空气的实际吸热量[14]：

QJ=[ταG-UL(tp-ta)]A

(4)

式中：τ为玻璃盖板透射率；α为吸热板的吸收率；A为吸热板面积，m2；UL为集热器总损失系数；ta为环境温度，℃。本文选用HT-SAC-01太阳能空气集热器，其透射率为0.72，吸收率为0.95，损失系数为2.66。

4) 储热罐数学模型。

当集热器吸热量大于用户需要的供暖量时，储热罐开始储存热能，其蓄热模型为

(5)

当集热器吸热量低于用户需要的供暖量时，储热罐开始释放热能，其放热模型为

(6)

式中：Qc为蓄热功率，W；Qf为放热功率，W；QX,max为储热罐的最大储热容量，J；QX,min为储热罐的最小储热容量，J。

5) 蓄电池数学模型。

当风光发电量大于负载用电量时，蓄电池开始充电，其充电模型为

(7)

当风光发电量低于负载用电量、建筑供暖负荷高于集热量与储热量时，蓄电池开始放电，其模型为

(8)

式中：E为蓄电池存储电能；Pc为充电功率；Pf为放电功率；η为蓄电池自放电率；ηc为蓄电池充电效率；ηf为蓄电池放电效率；Esoc,max为蓄电池额定容量；Esoc,min为蓄电池最小储能量。本文选用GFM-200蓄电池，其充放电率为0.7，最低放电深度为0.65，额定容量为200 A·h。

2 多目标优化模型

2.1 目标函数

高寒高海拔地区(如西藏)受地理位置与气候条件的制约，系统建造成本更高、维护更加困难。同时，这些地区的生态环境比较脆弱，系统建造还要考虑其环境效益。因此，本文在对风光互补热电联供系统进行优化时，选取系统成本、供电可靠性与当量CO2减排量为目标函数。

1) 系统总成本模型。

风光互补发电系统的总成本主要包括固定投资成本和维护费用2部分。其中，系统初始固定投资成本包括风力发电机组、光伏阵列、集热器、蓄电池组、逆变器等设备成本，相关设备的初始投资成本可表示为：

式中：NW为风力发电机组数量；NPV为光伏阵列的数量；NB为蓄电池的组数；AJ为集热器的面积，m2；VX为储热罐体积，m3。CW、CPV、CB、CJ、CX分别为风机、光伏阵列、蓄电池、集热器、储热罐的单价，分别为3000元、600元、1 500元、1 000元、1 500元。r为折旧率，取5%；Lf为系统工作年限，取20年。

风光互补发电系统的运行维护费用可表示为

(11)

式中：C′W、C′PV、C′B、C′J、C′X为风力发电机组、光伏阵列、蓄电池组、集热器、储热罐的运行维护费用系数。

将系统的总成本作为一个优化目标，即

F1(X)=Cbm+Com

(12)

2) 系统供电可靠性。

根据能量平衡原则与时间序列法，将评估时段以小时为单位，假定各时段内系统发电量与负荷量不变。负荷缺电率的具体表达式：

(13)

式中：fLPSP为全年负荷缺电率；ΔP(ti)为风光互补热电联供系统的逐时负荷缺口；PL(ti)为建筑逐时的总负荷需求；N为一年总的小时数。

由公式(13)可知，该数值越小，风光互补系统的供电可靠性越高。

3) 系统当量CO2减排量。

风光互补系统在运行过程中，将绿色可再生风能与太阳能转换为电能，不会对环境造成破坏。因此，相比传统火力发电系统，风光互补系统的发电量可以减少有害气体的排放。传统火力发电厂在发电过程中，排入环境的废弃包括CO2、CO、CH4、SO2与NOx等气体，将这些都折算成CO2，可以计算出风光互补发电系统的当量CO2减排量。

(14)

式中：Fco2、Fch4、Fco、FNOx、Fso2分别为CO2、CH4、CO、NOx、SO2转换成CO2的比例因子；mco2、mch4、mco、mNOx、mso2分别火电厂生产1 kW·h电力是排放的CO2、CH4、CO、NOx、SO2等气体的质量，如表1所示[15]。

表1 转换因子、电力生产所排放的温室气体量Table 1 Conversion factors, greenhouse gas emissions from electricity production

另一方面，风机、太阳能光伏阵列、蓄电池等设备在投入运行与维护过程将不可避免地对环境产生危害。在投入运行过程中，风光互补系统的CO2排放量可表示为：

EOM,CO2=PW,tEW,CO2+APV,tEPV,CO2+NB,tEB,CO2

(15)

式中：EW,CO2为单位风力发电年CO2排放量；EPV,CO2为单位面积光伏电池板年CO2排放量；EB,CO2为单位储能容量电池的年CO2排放量；PW,t为所有风力发电机年发电量；APV,t为光伏电池板总面积；NB,t为蓄电池总容量。风机CO2的排放量为18 g/(kW·h)，太阳能光伏电板的CO2排放量为33 g/(kW·h)，蓄电池的CO2的排放量为50 g/(A·h)。

综合考虑风光互补系统CO2减排量与生成量，以当量CO2年减排量作为系统环境效益的评估指标。

(16)

2.2 设计变量及约束条件

在对风光互补系统容量配置进行优化时，以风力发电机数量NW、光伏阵列数量NPV、蓄电池组数NB、太阳能集热器面积AJ以及蓄热罐容积VX等5个参数作为设计变量，即X=(NW,NPV,NB,AJ,VX)。

在优化过程中，考虑如下条件对设计变量的约束：

极端工况下，如夜间光伏阵列输出功率为0，风力发电机组输出功率应满足系统负荷的平均功率。

(17)

当白天风力很小时，风力发电机组几乎不工作，光伏阵列输出功率也应满足系统负荷的平均功率。

(18)

当风力发电机和光伏阵列的输出功率为零时，蓄电池应能保证系统负载正常运行n天，则所需蓄电池的数量为

(19)

式中：USOC为蓄电池正常工作电压；DODmax为蓄电池最大放电深度。

太阳能空气集热器的总吸热量应大于建筑所需的供暖负荷的60%，即

AJ≥0.6QGN/QJ

(20)

光伏阵列日平均发电总量与风机发电总量之和应能满足日平均负荷需求：

(21)

2.3 优化算法

风光互补热电联供系统多目标优化中，不同性能指标之间存在对立与竞争关系，通常不存在唯一的局部或全局最优解，而是许多非劣解的集合，即pareto解集。NSGA-II算法是根据生物遗传与变异演化过来的高级进化算法，不仅能更好地从种群中获得优良个体、有效避免种群早熟，而且大大降低计算复杂度，大幅提升了计算速度与鲁棒性。该算法的具体流程如图2所示。

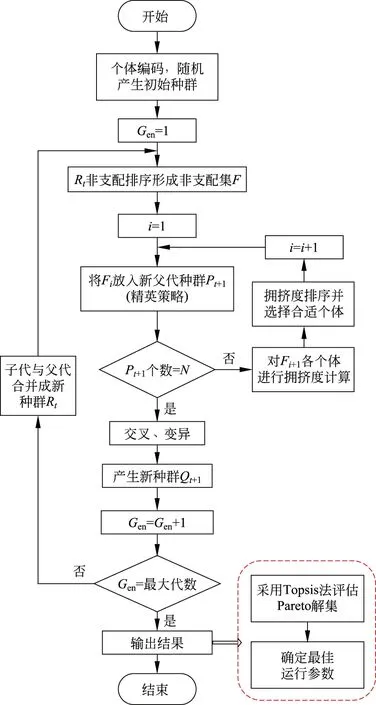
图2 NSGA-II算法计算流程Fig.2 Flow chart of NSGA-II

3 实例分析

本文以西藏自治区那曲市那曲县罗玛镇加贡村(北纬31°07′，东经92°05′)为例，对风光互补热电联供系统配置进行优化，以便更好地为当地村委会提供电能与供暖，改善当地的工作条件。优化过程中相关参数的设定见表2，且优化中假定各设计变量为连续参数，最后根据优化结果对其取整。

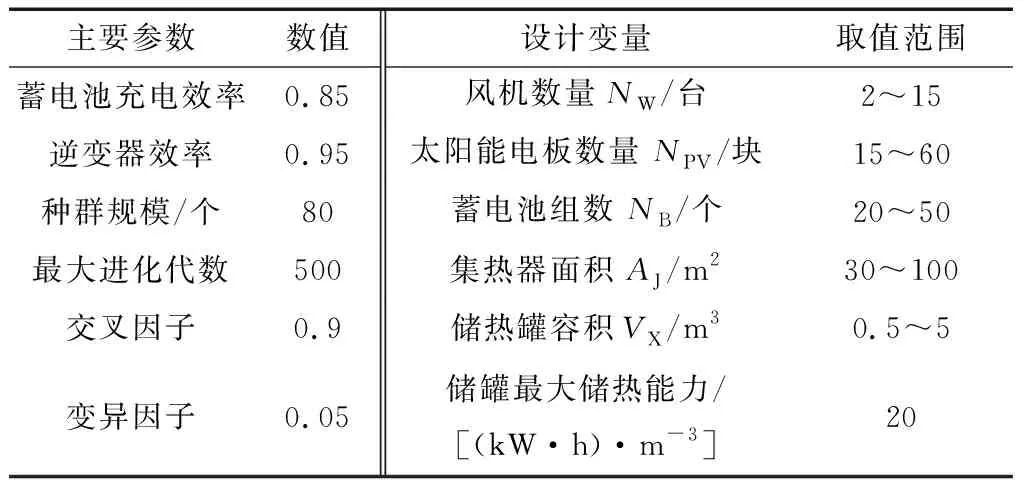
表2 优化过程中相关参数Table 2 Parameters for the multi-objective optimization

2018年，该地区的实时风速与光照强度如图3所示。

图3 当地逐时风速与光照强度Fig.3 Local hourly wind speed and light intensity

图3表明，那曲地区1～3月份的风速更高，平均风速约为6 m/s；7～9月的风力资源相对较少，平均风速约3 m/s。同时，该地区太阳能资源丰富，全年平均每日累计光照强度为5.1 kW·h/m2，且7～9月份的光照强度大，与风力资源形成了良好的互补性。

根据村委会用电负载及供能需求，计算该建筑的逐时用电量与热负荷，结果如图4所示。

图4表明，村委会用电主要集中在白天时段，晚上时段的负载较低；采暖热负荷分布与环境温度的分布规律正好相反，全年气温较低时段的热负荷更高。

在此基础上，采用NSGA-II计算程序对风光储多能互补系统开展多目标优化，所得Pareto解集对应的目标函数值如图5所示。

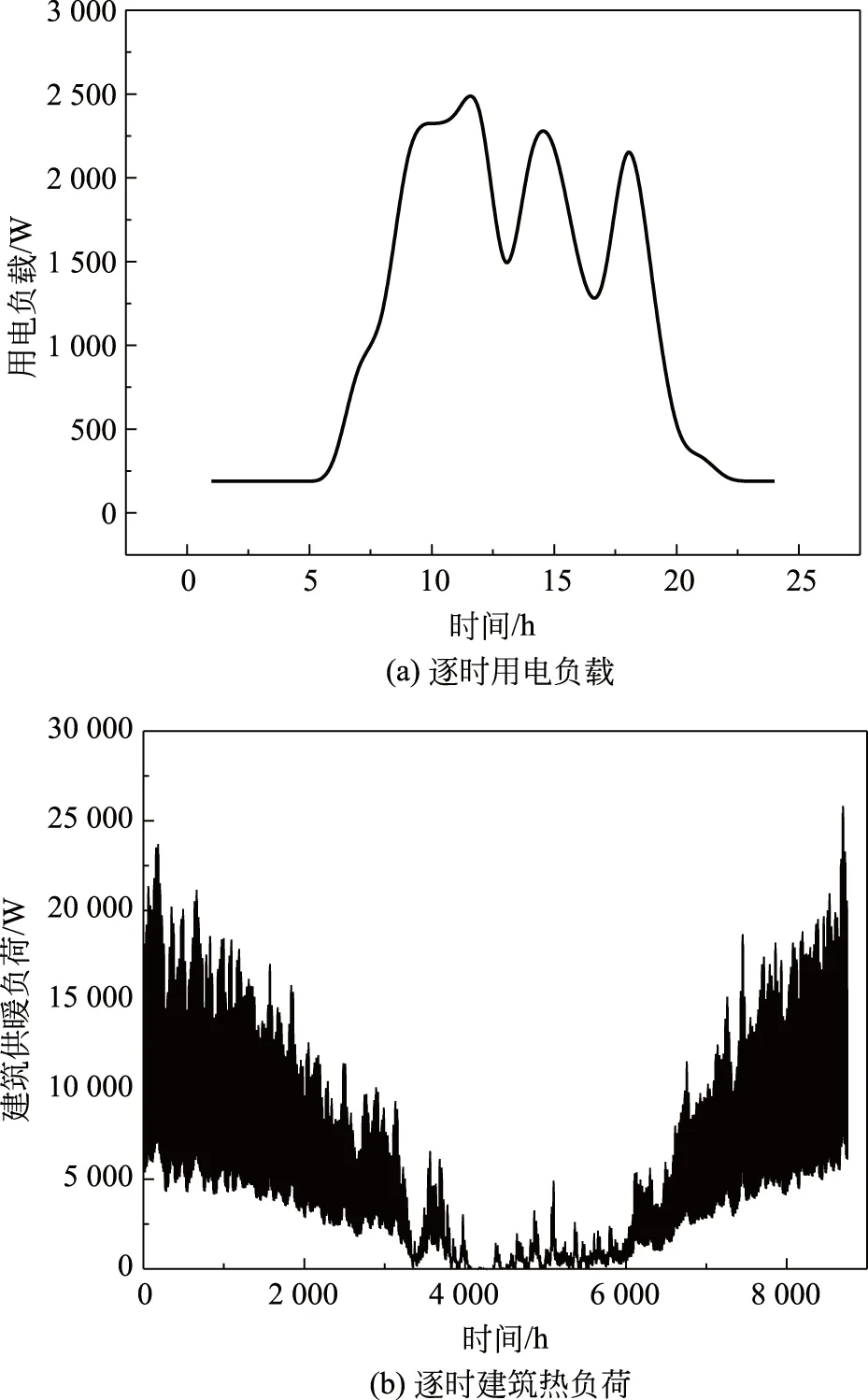
图4 当地逐时用电负载与建筑热负荷Fig.4 Local hourly power load and building heat load

图5 多目标优化的Pareto分布Fig.5 Pareto distribution of multi-objective optimization

图5表明，A点的投资成本最低而负荷缺失率最高，超过30%；B点的负荷缺失率最低(约0.6%)，而投资成本最高，接近28万。图5(b)中，C点的CO2年减排量最高，其负荷缺失率较低；D点的CO2年减排最低，而负荷缺失率最高。这说明系统投资成本与负荷缺失率存在对立竞争关系，而当量CO2减排量与负荷缺失率相一致。

基于“Topsis 决策法”的基本思想，对系统优化Pareto解集进行决策，所得的最终结果取整后如表3所示。

表3 多目标优化的最优解Table 3 Optimal results of multi-objective optimization

从表3中可以看出，最优工况下，风光互补系统的总体设备投资为16.2万，负荷缺失率为4.6%，每年可实现CO2减排95.4 t。通过系统优化设计，风光互补系统不仅可以提升其可靠性，而且可以降低CO2排放。

最优工况下，系统设备成本组成如图6所示。

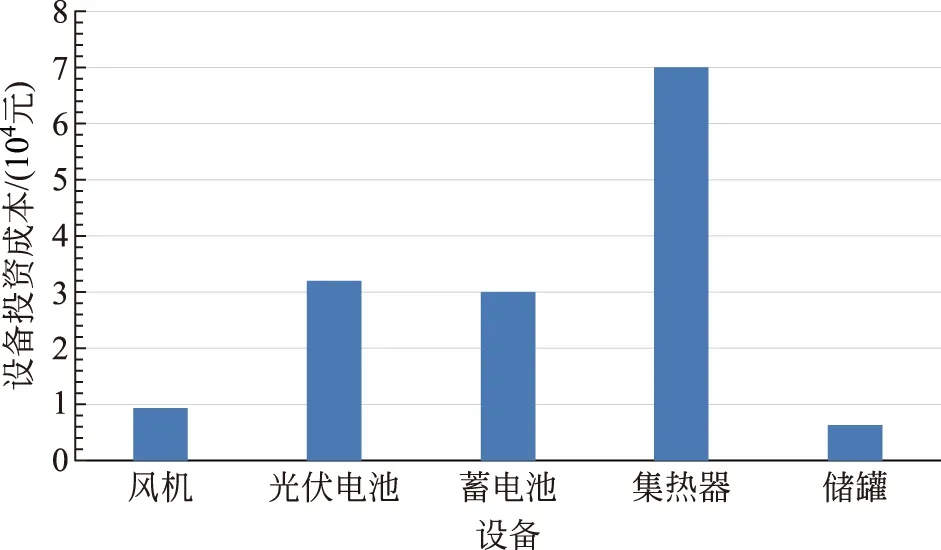
图6 最优工况下不同设备成本组成Fig.6 Cost composition of different equipment under optimal operating conditions

可以看出，系统设备成本中，集热器的总投资最多，约为7×104元，占设备总投资的50%；这主要是因为风光互补系统中集热器的数量最多，且集热器单位面积的价格也较高。系统中，光伏电池与蓄电池的投资基本相当，都小于集热器成本；风机与储热罐的占比都比较小，约占设备投资的10%。

为进一步了解最优工况下风光互补系统的运行特性，对系统性能进行计算与分析，图7给出了风机与太阳能光伏的逐月发电量情况。

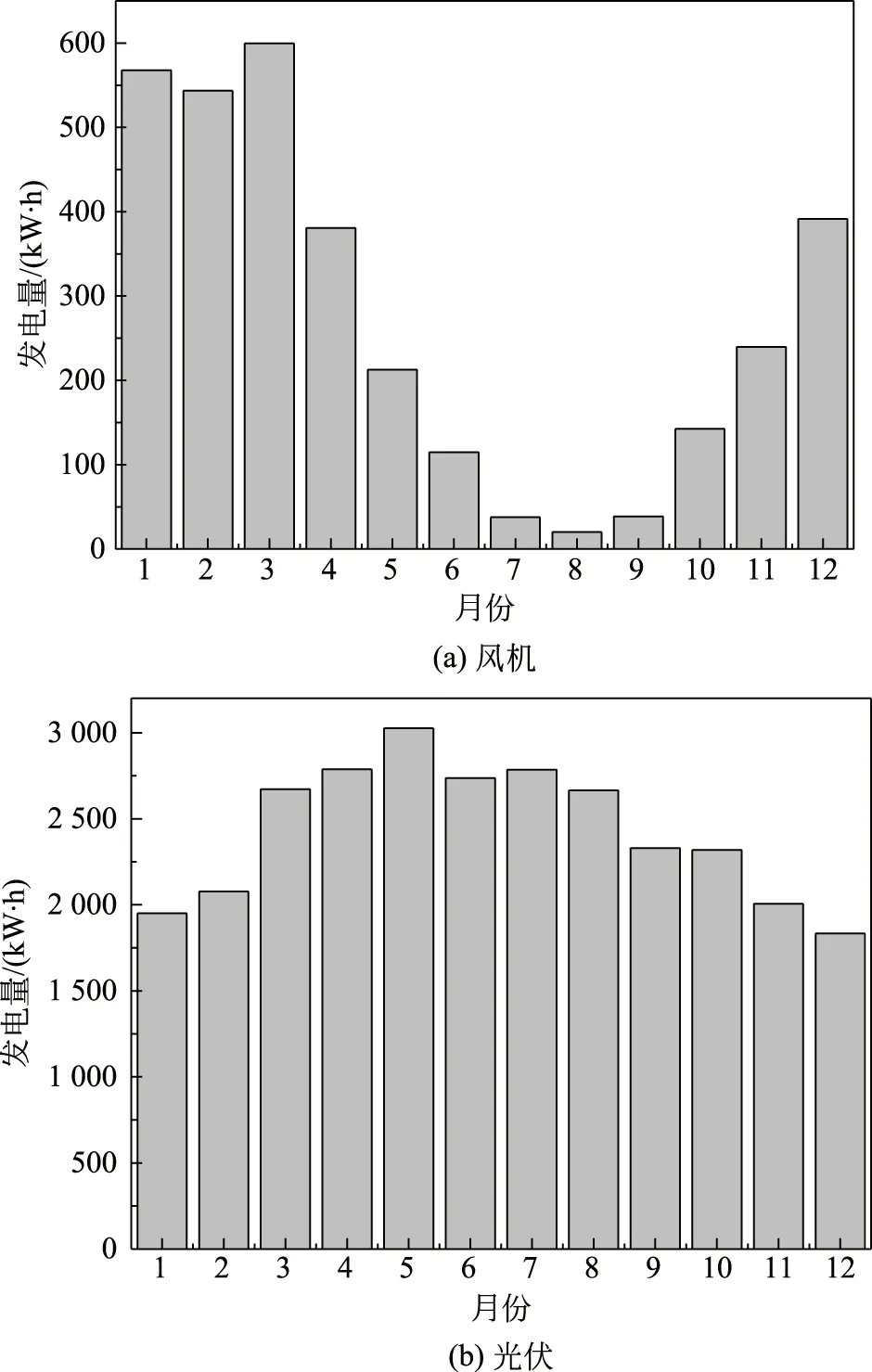
图7 最优工况下风机组逐月发电量Fig.7 Monthly power generation of wind turbine under the optimal condition

虽然一天当中风力资源具有较好的持续性，但是风力资源受季节的影响较大。如图7(a)所示，风机组在1～3月的输出电能最高，3台风机单月输出电量接近600 kW·h；7～9月的输出电能最小，风机组单月最低发电量仅20 kW·h；如图7(b)所示，光伏发电量在12月份最低(1 833 kW·h)，5月风最高(3 026 kW·h)，光伏发电量最高月份与最低月份的发电量仅相差40%。可以看出，光伏发电量波动较小，比风力发电更加均衡。因此，太阳能发电在整个风光互补系统中占主导地位。

系统逐时负荷缺失率如图8所示。

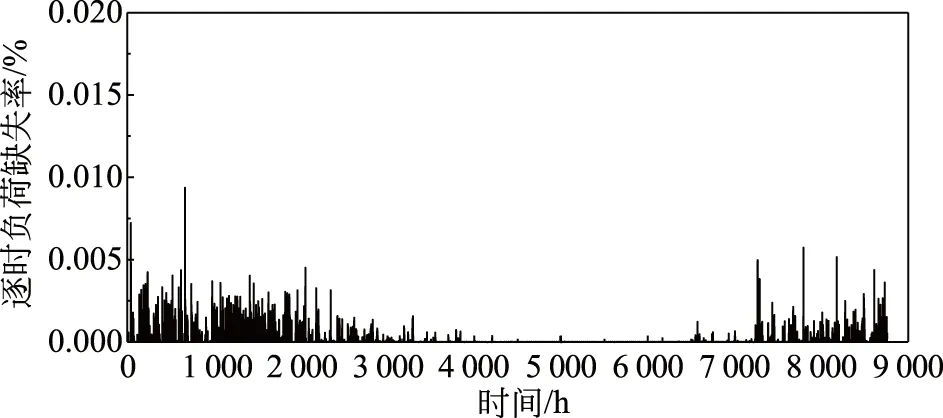
图8 风光互补系统逐时负荷缺失率Fig.8 Hourly load loss rate of wind solar hybrid system

从图8可以看出，风光互补系统的逐时负荷缺失率较低，且主要集中在一年中气候相对寒冷的时期。这主要是由于这一时期内的建筑供暖负荷较大，集热器吸热量、储热与储能单元难以满足建筑供暖需求，造成负荷缺失。根据前面优化结果可知，系统全年合计的负荷缺失率为4.6%，处于一个较低的水平，这也表明该容量配置能较好地满足村委会的用电与供暖需求。