基于少数类过采样的倾向得分匹配插补法
2021-01-26杨贵军孙玲莉
杨贵军,杜 飞,孙玲莉
(天津财经大学 a.统计学院;b.中国经济统计研究中心,天津 300222)
一、引 言
在社会经济问题研究中,学术研究越来越依赖于微观数据库,分析社会经济的运行机制以及数量关系。通过调查获得的微观数据常常存在一定程度的无回答,而且无回答是很难避免的。在大数据应用中,无回答发生更频繁。无回答会严重影响调查数据的质量以及分析结果的可靠性。多数统计方法和统计分析软件都是基于完整数据集设计的,如何有效地处理无回答成为获取可靠分析结果的关键。20世纪70年代统计学者极其关注无回答问题,并提出了在经济学和统计学相关领域中处理无回答问题的方法[1-2]。
处理无回答的方法主要划分为事前预防和事后补救两方面。鉴于数据收集过程中的条件限制,事前预防措施并不能从根本上解决无回答问题,因此多数方法从事后补救方面开展研究。无回答的事后补救措施大体可分为两类:一是基于设计角度对目标值进行估计的方法。Robins等基于对无回答概率的估计,提出估算目标值的加权法[3]。金勇进等则通过对无回答子总体进行追加调查的方式来减小无回答偏差[4-5]。Little等讨论了无回答的极大似然估计量[2,6-7]。二是对无回答进行插补的方法。Chapman等讨论了无回答的单重插补法[8-12]。Rubin将无回答的不确定性考虑在内,提出了多重插补方法,并作了进一步的讨论[1]。现在,多重插补法已成为处理无回答的最常用方法。
多重插补法将无回答的不确定性考虑在内,弥补单重插补法的缺陷,提高了插补结果的可靠性。常用的多重插补法可分为三类:第一类是基于协变量相近性匹配的插补法,例如:最近邻插补法、倾向得分匹配插补法;第二类是利用变量之间相关关系的插补法,例如:回归多重插补法[1-2,13]、预测均值匹配多重插补法[14-17];第三类是依据无回答统计性质的插补法,例如:DA多重插补法[16,18]、EMB多重插补法等[19-20]。其中,第一类插补方法在实际中应用范围最广泛。相较于其他直接基于协变量匹配的插补方法,倾向得分匹配插补法是利用倾向得分模型对无回答单元与回答单元进行倾向得分匹配,以此来提高插补效率。
倾向得分匹配(Propensity Score Matching,PSM)是由Paul和Rubin提出的基于反事实推断模型的协变量匹配方法[21]。其基本思想是利用Logit或Probit模型估计处理组与潜在对照组中单元的倾向得分,依据单元的倾向得分,搜索与处理组单元相匹配的控制组单元以构建对照组。PSM模型降低了匹配过程中由于混杂变量产生的影响,消除了系统性偏差,现已被广泛应用于经济学政策评价和因果推断等研究中。Little首次将PSM模型应用于处理无回答问题中,提出了倾向得分匹配插补法(简记为PSM插补法),将无回答单元划为处理组,回答单元划为对照组,根据倾向得分的相同或相近,将匹配的回答单元目标变量值作为无回答单元的插补值[22]。PSM插补法保留了PSM模型匹配效率高、不易受混杂变量影响的优点,提高了插补的准确性。然而,在实际应用中,无回答率往往较低,明显低于回答率,无回答单元数量与回答单元数量相差较大,造成Logit模型会倾向于误判为多数单元的类别,降低PSM插补法的可靠性。
针对类别数据的非平衡问题,目前最常用的方法是随机欠抽样和随机过抽样。随机欠抽样方法通过随机剔除部分多数类单元来改善数据集的非平衡程度,但会造成一定程度的信息损失。随机过抽样方法则通过随机复制少数类单元,使各类单元数达到平衡,但该方法会导致模型出现过拟合现象。Chawla等针对上述两种方法的缺陷提出少数类过采样(Synthetic Minority Over-sampling Technique,SMOTE)算法,保留所有多数类单元,并在相距较近的少数类单元之间线性合成新的少数类单元,以改善数据集的非平衡程度[23]。因而,SMOTE算法既保留了所有数据的信息,又在一定程度上避免了过拟合现象的出现。
综上,针对PSM插补法在处理无回答单元数量与回答单元数量相差较大情况下插补效果不佳的问题,本文创新性地将SMOTE算法的思想应用于解决插补问题,提出了一个新的PSM插补方法,并通过统计模拟和实证分析,在仅考虑单一目标变量存在无回答的情况下,比较SMOTE-PSM插补法与常用插补方法的插补效果,并分析不同无回答率、插补重数和误差分布对插补效果的影响,为解决在实际应用中的无回答问题提供更好选择。
二、基于SMOTE算法的PSM插补法
下面首先总结SMOTE算法和PSM插补法及其性质,再给出基于SMOTE算法的PSM插补法。
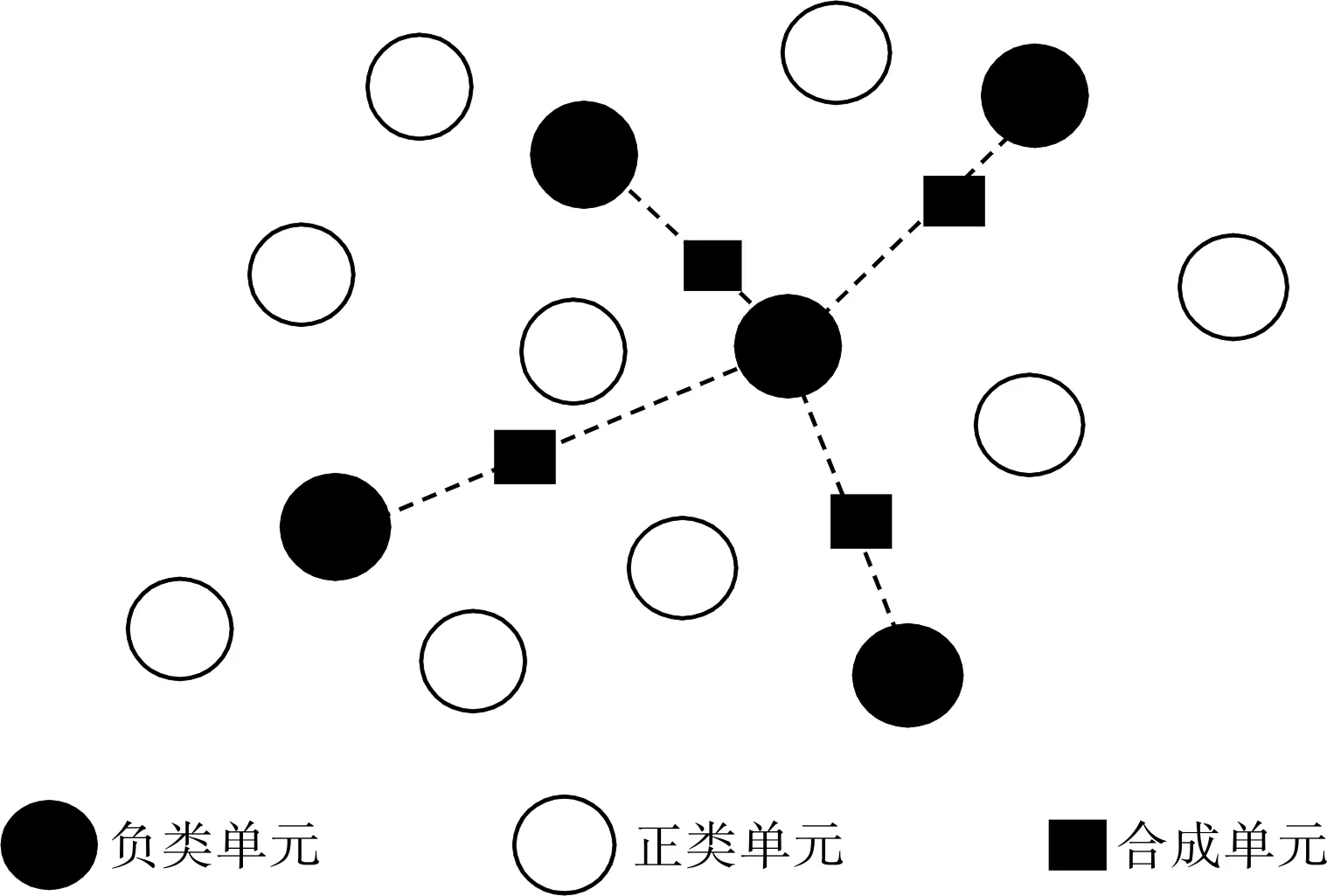
图1 SMOTE算法基本原理
(一)SMOTE算法
SMOTE算法是由Chawla针对非平衡分类数据提出的,其基本原理详见图1。在非平衡分类数据中,多数单元类称为正类,少数单元类称为负类。由于正负两类单元数量相差较大,往往造成传统分类模型的分类精度下降,特别是对于负类单元,分类模型无法通过训练集数据充分拟合其内在规律,导致分类精度相对低。SMOTE算法是目前较为经典的处理非平衡分类数据的一种过抽样方法,不同于仅对负类单元进行简单复制的随机过抽样方法,而是在相距较近的负类单元之间线性插值产生新的合成单元,平衡分类数据集,提高分类模型准确度。
SMOTE算法的基本假设为:距离较近负类单元之间的单元仍为负类,通过负类的合成单元来改善数据集的平衡程度。其具体过程如下:
第一步,确定单元合成率r。假定正类单元个数为n+,负类单元个数为n_,为使数据集类别平衡,需要产生负类的合成单元数ns=n+-n_,则单元合成率为:
(1)
第二步,计算负类单元之间的距离,选取近邻单元。不失一般性,设dij表示负类单元xi与xj之间的欧式距离,对于每一个负类单元xi(i=1,2,…,n_),与其他负类单元的距离向量记为Di=(di1,…,dij,…,di(n_-1)),从中选取dij中最小的b个单元作为近邻单元。
第三步,产生负类的合成单元。在负类单元xi选取的b个近邻单元中,随机抽取r个单元记为xl(l=1,2,…,r),利用xi与xl按照式(2)产生新的合成单元pil:
pil=xi+rand(0,1)×(xl-xi)
(2)
其中,rand(0,1)表示(0,1)之间的随机数。最后将每一个负类单元xi的r个合成单元合并到原数据集中,形成新数据集。
综上,SMOTE算法在负类的邻近单元之间通过随机线性插值产生负类的合成单元,构造的新数据集不仅好于原数据集的分类平衡程度,还具有更丰富的负类单元信息,以改善传统分类模型的拟合效果,提高分类精度。同时,SMOTE算法还避免分类模型出现过拟合现象。
(二)PSM插补法
Little将PSM模型应用于无回答的插补过程中,提出PSM插补法。PSM插补法的步骤主要分为匹配步和插补步,具体过程如下:
匹配步:将数据集中无回答单元视为处理组,回答单元视为对照组,回答与否的标记作为响应变量,利用Logit或Probit模型对每个单元的倾向得分进行估计,将倾向得分相同或相近的无回答单元与回答单元视为匹配单元。假定数据集样本量为n,观测变量为{Y,X},其中Y为被解释变量,X为解释变量。本文仅考虑被解释变量Y存在无回答的情况,记Y中的无回答单元和回答单元为{Ymis,Yobs},样本量为{nmis,nobs},与其对应的解释变量为{Xmis,Xobs},无回答单元集为{Ymis,Xmis},回答单元集为{Yobs,Xobs}。定义标识变量为T,其中无回答单元标记为1,回答单元标记为0,即对于i=1,2,…,n,
利用标识变量T与解释变量X构建倾向得分模型,并计算每个单元的倾向得分拟合值。这里,选择最常用的Logit模型作为倾向得分模型,有:
(3)
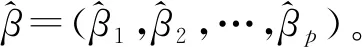
(4)

插补步:计算无回答单元与回答单元的倾向得分差值,将差值最小的m个回答单元的被解释变量值作为无回答单元的m重插补值。假设无回答单元与回答单元的倾向得分差值为si,j,即对于i=1,2,…,nmis,j=1,2,…,nobs,
(5)
针对每个无回答单元,将倾向得分差值进行排序,
si,1≤si,2≤…≤si,m-1≤si,m≤si,m+1≤…≤si,nobs
(6)
选取差值最小的m个回答单元的被解释变量观测值作为无回答单元的m重插补值。
PSM插补法利用倾向得分对无回答单元与回答单元进行匹配,避免了混杂因素的影响,提高了插补的效率和可靠性。
(三)SMOTE-PSM插补法
在实际应用中,人们都尽可能降低无回答率,导致调查数据的无回答单元数量与回答单元数量差异往往较大,PSM模型的分类精度下降。这里,继承SMOTE算法处理非平衡数据的优势,提出基于SMOTE算法的PSM插补法。目前,处理无回答的方法是基于无回答缺失机制的假定。在大多数的实际应用中,随机缺失机制(简记为MAR)最为常见,故选择随机缺失机制的假定。由MAR机制的定义可知:
p(T=1|Y,X)=p(T=1|X)
(7)
即变量的无回答概率仅依赖于完全观测变量X,与无回答变量Y无关。例如:居民收入调查中,受访者收入数据的无回答概率与其年龄有关,年龄是完全观测变量,则收入数据无回答往往为MAR机制。本文提出的SMOTE-PSM插补法先采用SMOTE算法利用无回答单元合成新的单元,改善数据集的非平衡程度,再通过PSM插补法对无回答单元与回答单元进行匹配和插补。新方法的具体步骤如下:
第一步,产生合成单元集。根据回答单元数量与无回答单元数量确定合成率r,对于每个无回答单元{ymis,i,Xmis,i},选取距离最近的b个无回答单元,从中随机抽取r个单元{ymis,l,Xmis,l},l=1,2,…,r,按照式(2)产生新的合成单元集{ymis,il,Xmis,il}:
{ymis,il,Xmis,il}={ymis,i,Xmis,i}+rand(0,1)×({ymis,l,Xmis,l}-{ymis,i,Xmis,i})
(8)
将合成单元集与原数据集组成新数据集{YS,XS}。
第二步,利用PSM插补法对无回答单元进行插补。数据集{YS,XS}包含回答单元、无回答单元和合成单元。基于PSM插补法,将回答单元标记为0,划为对照组;将无回答单元和合成单元标记为1,划为处理组。对于k=1,2,…,n+r×nmis,标识变量T(YS)定义为:
利用标识变量T(YS)与解释变量XS,构建倾向得分模型,计算每个单元的倾向得分拟合值,再对无回答单元与回答单元进行匹配。将每个无回答单元的倾向得分差值最小的m个回答单元的被解释变量观测值作为该无回答单元的m重插补值。
本文将SMOTE算法处理非平衡分类数据集的优势扩展到PSM插补法中,创新性地提出了SMOTE-PSM插补法,解决了无回答单元与回答单元在数量不平衡时PSM模型的拟合精度问题。本文提出的SMOTE-PSM插补法不仅保留了PSM插补法不易受混杂变量影响的优点,也继承了SMOTE算法的优势,保证了插补的精度。
三、SMOTE-PSM插补法的统计模拟研究
(一)统计模拟的模型设定
鉴于无回答真实值的不可获得性,本文利用统计模拟方法研究SMOTE-PSM插补法的统计性质。设定线性模型产生完整数据集,依据MAR机制设置无回答单元,利用SMOTE-PSM插补法对无回答单元进行多重插补,评价线性模型系数估计的统计性质。设定的线性模型为:
Y=β0+β1X1+β2X2+β3X3+β4X4+ε
(9)
其中,解释变量设定为两种类型,将X1、X2设定为连续变量,分别服从正态分布N(1,4)和N(10,4),将X3、X4设定为离散变量,分别服从二项分布B(1,0.8)和B(1,0.6);截距项和解释变量系数分别设定为β0=1,β1=10,β2=1,β3=1,β4=2;误差项ε的分布分别设定为正态分布、T分布和Cauchy分布,以对不同误差分布假定下的插补效果进行比较,设定数据集的样本量为100。

(二)模拟结果比较分析
1.不同插补方法的模拟结果与分析
在MAR机制下,单元的无回答概率仅依赖于完全观测变量,与无回答变量无关。本文选取X1和X3两个不同类型的变量作为无回答概率的依赖变量,对单元进行无回答设定,分别采用SMOTE-PSM插补法和其他比较方法对无回答单元进行多重插补。在无回答概率依赖连续变量X1的情况下,选择小于变量X1的给定无回答比率分位数的单元,将目标变量值设定为无回答。在无回答概率依赖于离散变量X3的情况下,借鉴Kropko的方法,利用Logit模型将变量X3的值转换为概率值pi,再按照依赖于连续变量X1的情况进行设定单元的无回答。在采用SMOTE算法产生新的合成单元时,若无回答率为5%,单元合成率r为18,近邻个数b选为3;若无回答率为20%,单元合成率r为3,b为5。表1和表2分别给出单元无回答概率分别依赖于连续变量X1和离散变量X3的模拟结果,其中RE表示系数估计的相对误差,MSE表示系数估计的均方误差。
表1和表2中的模拟结果显示,在无回答率与插补重数的多种组合中,与其他插补方法相比,基于SMOTE-PSM插补法的系数估计的相对误差和均方误差最小。在无回答率为5%时,SMOTE-PSM插补法明显优于其他插补方法。
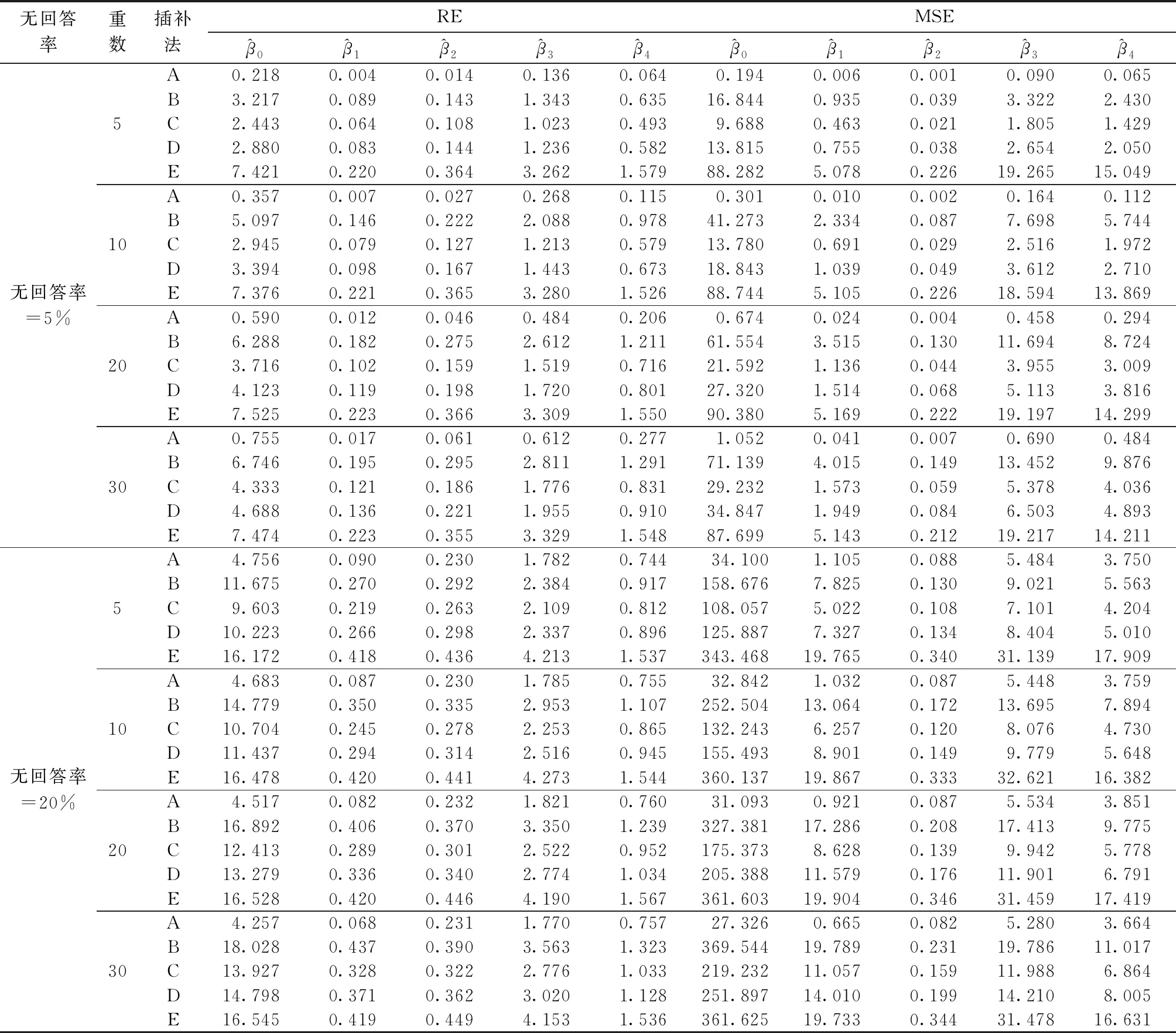
表1 无回答概率依赖于连续变量X1的模拟结果

表2 无回答概率依赖于离散变量X3的模拟结果
由表1和表2的比较分析可知,在无回答率一定或插补重数一定的情况下,五种插补方法的模拟结果表现特征相同。在给定无回答率的情况下,基于PSM插补法、响应倾向得分匹配插补法和最近邻插补法的系数估计相对误差和均方误差,都随着插补重数增加,呈现出递增趋势。而回归插补法相应的相对误差和均方误差未呈现明显的变化趋势。SMOTE-PSM插补法在不同无回答率下呈现不同的特征。在无回答率为5%的情况下,基于SMOTE-PSM插补法的系数估计相对误差和均方误差无明显递减趋势;而在无回答率为20%的情况下,插补效果呈现下降趋势。在插补重数为30时,插补效果更优良。从相对误差和均方误差的变动幅度来看,PSM插补法和最近邻插补法受插补重数的影响较大,响应倾向得分匹配插补法和回归插补法次之,SMOTE-PSM插补法的相对误差和均方误差变动幅度最小,受插补重数的影响小。
在给定插补重数的情况下,基于五种插补法的模型系数估计相对误差和均方误差,在无回答率为20%的情况下均高于无回答率为5%的情况。其中,基于PSM插补法和回归插补法在两种给定无回答率下的系数估计相对误差和均方误差的变动幅度较大,响应倾向得分匹配插补法和最近邻插补法次之,SMOTE-PSM插补法的变动小,说明无回答率对SMOTE-PSM插补法的影响小,插补效果较为稳健。
综上可知,无论单元无回答概率依赖于连续变量还是离散变量,在无回答率与插补重数的多种组合中,基于SMOTE-PSM插补法的系数估计的相对误差和均方误差最小,并且在不同无回答率和插补重数下,系数估计的相对误差和均方误差变动幅度最小,插补效果稳定。
2.不同误差分布假定下的模拟结果
为了分析误差分布对SMOTE-PSM插补法的插补效果影响,分别选择T分布、Cauchy分布和正态分布作为误差分布,进行模拟研究。为了简洁展示模拟结果,给出无回答率20%、插补重数5组合下的模拟结果,见表3和表4。其中,非正态误差分布假定下的系数估计采用极大似然估计方法。

表3 不同误差假定的模拟结果(无回答概率依赖于连续变量X1)

表4 不同误差假定的模拟结果(无回答概率依赖于离散变量X3)
表3给出单元无回答概率依赖于连续变量X1的五种插补方法的模拟结果。从系数估计的相对误差和均方误差来看,在三种误差分布假定下,回归插补法的插补效果最差。基于SMOTE-PSM插补法的系数估计相对误差和均方误差最小,受误差分布影响小,系数估计量的变动幅度最小。表4给出单元无回答概率依赖于离散变量X3的五种插补法的模拟结果,与单元无回答概率依赖于连续变量X1的模拟结果相似。从系数估计的相对误差和均方误差来看,回归插补法、最近邻插补法和PSM插补法的插补效果较差,且回归插补法和PSM插补法易受误差分布的影响。基于SMOTE-PSM插补法的系数估计的相对误差和均方误差明显低于其他四种插补法,受误差分布影响最小,误差分布对系数估计的变动幅度影响最小。综上可知,在多种误差分布假定下,SMOTE-PSM插补法的插补效果最优,系数估计的相对误差和均方误差小,变化幅度小,插补效果稳定。
由上可知,本文所提出的SMOTE-PSM插补法在各误差分布假定下的插补效果最优,并且不同误差分布假定下的系数估计相对误差和均方误差变化幅度小,受误差分布的影响小,插补效果稳定。从不同误差分布来看,SMOTE-PSM插补法在正态分布和T分布假定下的插补效果较好,且两者较为接近。
四、SMOTE-PSM插补法的实证研究
下面验证SMOTE-PSM插补法在Grilic(1)数据下载网址为:https:∥github.com/Stata-Club/Sharing-Center-of-Stata-Club。真实数据集中的应用效果。Grilic数据集由12个观测变量和758个观测组成,用于研究年轻男子工资的影响因素。这里,选取Lw(工资对数)作为被解释变量,Kww(在“Knowledge of the World of Work”中的测试成绩)、IQ(智商)、Smsa(大城市虚拟变量,住在大城市=1)和Mrt(婚姻虚拟变量,已婚=1)作为解释变量,其中Kww和IQ为连续型变量,Smsa和Mrt为离散型变量。选择的线性模型为:
Lw=α0+α1Kww+α2IQ+α3Smsa+α4Mrt+ε
(10)
表5给出了Grilic数据集在MAR机制下利用SMOTE-PSM插补法的实证结果。Grilic完整数据集的模型系数估计值在显著性水平5%下均显著为正,表明年轻男性群体中,在“Knowledge of the World of Work”测试中的成绩越高,智商越高,所能获得的期望工资越高;居住在大城市比居住在小城市获得的期望工资高;已婚状态比未婚状态获得的期望工资高。第3~18行给出了从Grilic数据集中简单随机抽取100个观测依赖于解释变量Kww、IQ、Smsa、Mrt缺失情况下的实证结果,由于从Grilic完整数据集中重复随机抽取100个观测进行无回答设定,会导致系数估计的方差扩大,大于选用完整数据集的系数估计标准误。
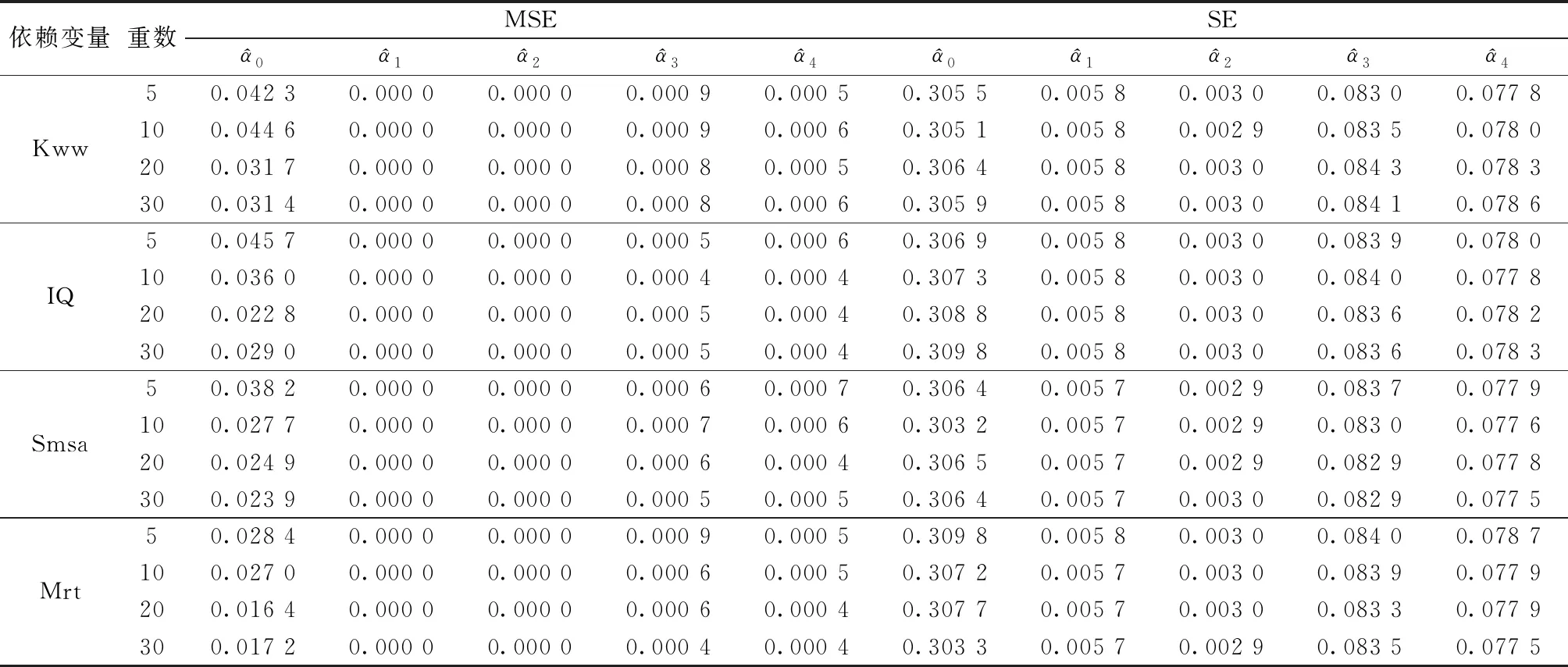
表5 Grilic数据集的分析结果
五、结 论
微观调查数据集中常常存在一定程度的无回答,且很难避免。无回答会严重影响调查数据的质量和分析结果的可靠性。PSM插补法作为处理无回答数据的常用多重插补方法,利用PSM模型对无回答单元与回答单元进行匹配,实现无回答数据的插补,具有不易受混杂变量影响的优点。但是,实际应用中,调查数据的无回答率往往较低,无回答单元数量与回答单元数量相差较大,会造成PSM模型的匹配效果下降,降低PSM插补法的可靠性。
本文为了提高实际应用中无回答单元数量明显低于回答单元数量情况下PSM插补法的插补效果,将SMOTE算法处理非平衡数据集的优势引入PSM插补法,提出基于合成少数类过采样的倾向得分匹配插补法,即SMOTE-PSM插补法。新插补法保留了PSM插补法的优点,并融合了SMOTE算法的优势,改善了非平衡分类数据的拟合性能,提高了插补效果。统计模拟结果演示,SMOTE-PSM插补法的插补效果明显提高,且不易受误差分布的影响,提高了插补的有效性及稳健性。实证结果表明,SMOTE-PSM插补法在实际数据Grilic中同样具有较好的可应用性,能够有效解决数据无回答问题,得出可靠的分析结果。本文的研究为PSM插补法在非平衡分类数据中的应用提供了新思路,可将其推广到政策评价和因果推断等数据分析中。
