考虑不同电价的电动汽车充电服务最优网格划分

覃文泽，李 强，姚 方，文福拴

(1.山西大学电力与建筑学院，山西 太原 030013；2.国网山西电力公司经济技术研究院，山西 太原 030000; 3.浙江大学电气工程学院，浙江 杭州 310027)

0 引言

为了应对环境问题和日益严峻的能源危机，电动汽车(electric vehicle，EV)作为一种节能环保的交通工具受到大众的关注。EV噪声低、无污染、效率高、方便耐用，受到广大消费者青睐。EV市场不断增大，截止2019年底，我国纯EV已有310万辆，2025年我国EV保有量预计将会达到2 390万～2 820万辆[1]。但大量EV的使用会给电力系统带来影响，如电力设备使用寿命降低[2]、配电网电压水平受到影响[3]，也会导致用户排队时间过长等情况出现[4]。为了减轻对电力系统的影响和提升用户的日常体验，充电设施的合理规划和布局是重要措施。

针对充电站的选址定容，已有学者和技术人员做了相关研究。常见的分析对象主要有排队等待时间和碳排放[5-7]、对配电网的影响[8-10]、经济性[7,9-12]以及交通流量[13]。文献[5]结合排队论，以前往充电站、排队、充电三者时间之和为约束，以充电期望值最大为目标函数建立选址定容模型。文献[6]综合考虑排队时间和EV里程约束，以用户总效用最大为目标提出选址模型，并采用免疫优化算法求解。文献[7]以充电站建设成本、用户前往充电站的碳排放和时间、排队时间为目标建立模型，提出基于需求点栅格化的求解方法。文献[8]将充电站规划与配电网调度相结合，建立双层选址定容模型。文献[9]建立了路径选择和交通满意度评价模型，并以总成本最小、网损最小和交通满意度最高为目标建立了选址定容模型。文献[10]基于配电网扩展规划模型，建立总投资成本、运行成本最小的多阶段模型，将网损分段线性化处理并提出两层求解方法。文献[11]运用动态交通网络思想建立了确定充电站布局的优化模型，以用户和充电站成本之和最小为目标函数。文献[12]利用几何方法选择初始站址，并用鲶鱼粒子群算法优化，根据全社会成本最优选取方案。文献[13]以行驶里程约束为下层，以路径流量最大为上层，并用启发式算法求解。

基于上述文献，本文首先分析了充电设施的经济性，然后考虑谷充电电价和放电电价对用户的影响程度，根据不同类EV的出行特性和充放电特性建立负荷模型。为了引导用户前往合适地点充电，结合Voronoi原理求解充电站站址，得到EV充电服务的最优网格划分，在此基础上，以最大允许排队时间为约束计算各充电站设备数量，并计算不同充放电价格下充电设施的经济性。

1 经济性分析

1.1 投资成本

按照生命周期成本理论，EV充电站的生命周期分为建设期、运营期和退出期[14]。本文主要是对新建充电站进行规划，不考虑退出期。

充电站的投资成本可表示为

(1)

式中：ΩK为充电站集合；Cbi和Coi分别为建设成本和运营成本。

式中：d=1和d=2表示快充和慢充；ndi为充电站i所需充电桩的数量；Cevd为单个充电桩的价格，快充和慢充均只使用一种型号的充电桩；Cf和nfi为放电设备的价格及数量；Chi为充放电辅助设备成本，包括变压器和整流滤波装置等；Czi为建筑成本；ui是0-1变量。

式中：Pc,d、cosφd、ηd分别为充电桩的输出功率、功率因数和效率；ηvt为变压器效率；k为同时充电系数；tcs为充电桩工作小时数；Pce和tce为其他用电设备的功率和工作小时数；Cp为充电站从电力公司购电的价格；Coth为其他成本，包括设备检修维护、折旧费用和人工费用等，由于此成本不明确，将建设成本按照一定比例进行估算[15]。

1.2 投资效益

本文考虑投资效益的是社会总效益。由于社会生产、生活规律，电网负荷的峰谷差客观存在，EV作为分布式电源，按照电力公司期望的方式进行有序充放电，可以有效减小峰谷差，降低电网的运行成本。对于EV用户，大规模的无序充电会导致充电站利用效率低下，充电高峰时段排队时间过长，而有序充电可以有效改善这一点。单量EV放电，对电力系统影响很小，所以需要大量EV同时放电形成集成效应。而频繁的充放电会对电池产生不可逆的损伤，因此要用较高的放电价格保证用户的利益。充电站从电网购电向用户售电，售电价格高于购电价格以保证自身效益，但售电价格过高时无法调动用户在夜间充电，可能会进一步增大电网高峰负荷。

B=ΔC+Bf+Bs

(7)

式中：ΔC为电力系统运行成本的降低，主要体现为峰谷差和发电成本的下降；Bf为用户参与放电得到的收益；Bs为充电站售电收益；tq和Tmax为用户充电时的排队时间和允许排队时间上限。

2 充电负荷模型

充电负荷的计算是充电站合理规划的前提，本文主要考虑不同区域之间的转移概率、不同类型EV的出行特性和充放电特性以及不同电价对用户充放电意愿的影响。

2.1 区域划分

按照功能和民众行为规律的差异，可以将城市大致划分为居住区R(resident)、工作区W(work)、商业区B(business)、社交休闲区SR(social and recreational)和其他事物区O(other)五大类[16]。居住区主要指居民小区，小区内充电负荷大多是下班回家后私家车充电引起，到次日上班间隔时间较长，使用慢充完全可以满足用户充电需求，居住区内按照一定比例在现有停车场内设置慢充桩和相应放电设备，不需新建建筑物。商业区主要包含购物中心、银行、酒店、快餐店等，交通流量大，工作区主要包含写字楼、工厂等，社交休闲区主要包含公园、电影院等，其他事物区主要包含学校、医院、政务机关等，若在以上区域建设充电站，快充桩和慢充桩均需设置。

2.2 电动汽车出行特性分析

2.2.1 私家车

(1) 首次出行时刻。

受限于电池技术的发展，EV续航里程无法媲美传统燃油汽车，但也足够满足城市内用户日常使用。因此，EV与燃油车的差别更多地体现在能源使用上，出行规律差别不大。根据美国交通部的统计[17]，私家车每日首次出行时刻T分布为

(10)

式中：a1=0.136；b1=7.546；c1=0.998；a2=0.109；b2=9.386；c2=3.7。

(2) 出行链。

私家车出行规律较为固定，可以用出行链来描述其出行序列。相当一部分私家车主要用于工作地点与住宅之间的通勤，出行链描述为R-H-R。出行链较长时，一般工作区W只出现一次，商业区B和社交休闲区SR可能多次出现。典型出行链及其概率见表1[17]。

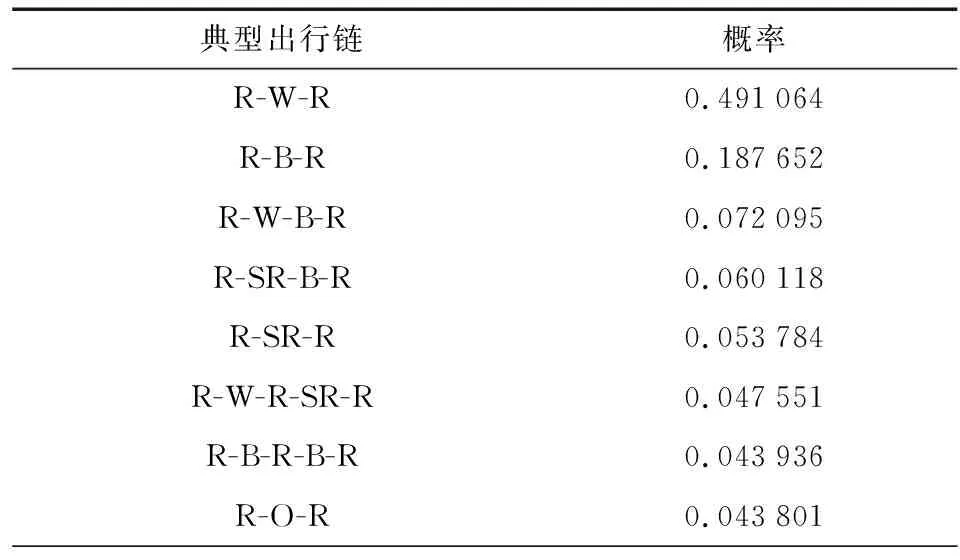
表1 典型出行链及概率Table 1 Typical trip chain and probability

(3) 停留时间。

私家车从首次出行开始，达到不同的目的地可能会停留不同的时间，如出行链R-W-R，用户达到工作区后可能会停留8 h左右，之后再次回到家中。用户在不同地点停留时间tp的概率分布见表2[17]，其中停留在居住区R是指回到家中经一段时间停留后继续出行。

表2 不同目的地停留时间概率分布Table 2 Probability distribution of residence time at different destinations

(4) 有序充电和放电概率。

充放电是长期且频繁的行为，用户可以选择是否签订协议。签订协议的用户按照协议规定时间充放电并定期获得补贴，未签订协议的用户则可以自由决定充放电行为。本文只考虑非协议用户，其充放电行为与电价密切相关，只有电价到达一定程度时，用户才会出于利益考量改变充放电习惯。分时充电电价有利于将部分充电负荷从高峰转移到低谷，在峰电价一定的情况下，转移比例与谷电价高低相关。期望放电电价与用户荷电状态相关，当实际放电电价高于期望值时，用户才会参与放电。按照理性程度将非协议用户分成3类[18]：非理性(Ⅰ类)、理性(Ⅱ类)和有限理性(Ⅲ类)。Ⅰ类用户不受充放电电价影响，不参与有序充电和放电。Ⅱ类用户参与有序充电的概率Poc与谷电价Pv负相关，期望放电电价Pexp与用户荷电状态S负相关。Ⅲ类用户在Pv和S过低时，出于边际效益降低和对行程的焦虑，其参与有序充电的概率比Ⅱ类用户低，期望放电价格比Ⅱ类用户高。大部分车主属于Ⅲ类用户。

(5) 充放电负荷。

为减少排队及往返充电站时长，尽可能减少充电次数，用户仅在预计到达下一目的地后电量不足以保留最小电量Smin应急和结束1天的行程2种情况选择充电，其余情况不充电。其中，结束1天行程后，有序充电用户在谷电价时段慢充，无序充电用户中有个人充电桩的回家后立即开始慢充，无论是否在谷电价时段，没有个人充电桩且电量较多时可选择不充电，电量较少时立即前往集中充电站充电。

不论是否参与有序充电，当电量较多且放电电价Pf高于期望电价Pexp时，用户参与放电，放电时间不宜过长，以放电后仍能保证结束1天行程后保留Smin为上限。

(11)

式中：Si,1和Si,2为行程i开始和结束时的荷电状态；C为电池容量；u为每公里耗电量；di为行程i的公里数。

式中：Pw1和Pw2为慢充和快充功率；η1为充电效率；Smax为EV最大荷电状态；t1为使用慢充充满用时；t2为使用慢充充至行程i+1结束后保留Smin的最小用时；t3为使用快充充满用时。

(15)

式中：Pw 3和η2为放电功率及效率；tc为充电时间；tf为放电时间；S′和t4为期望放电价格与实际价格相等时的荷电状态及放电用时；t5为保留行程i+1耗电和Smin前提下可放电的最大时间；ti,2为行程i结束时刻；tb为系统接受EV放电的结束时刻。

2.2.2 出租车

出租车运营实行两班倒，每班持续12 h，充电1次难以满足需求，应在换班前充满电[19]，运营中载客结束充电条件为

Si,2≤Smin

(21)

出租车出行随机性大，目的地由乘客指定。美国交通部在2017年统计了923 573段行程[20]，其中包含每段行程中用户在出发前正在做的事和出行目的，结合2.1中的区域划分，可以得到每段行程在各区域之间的转移情况。例如一段行程中用户出发前在做家务，出行目的是上学，可以认定此行程是从居住区R转移到其他事务区O。除去无效数据，共有280 610段行程是从R出发，其中有41 082段行程目的地为O，根据统计数据得到从R转移到O的概率为0.146 4。同理，据统计得到各区域间转移概率矩阵P为

1.3.1 卵巢损伤因素 主要包括卵巢病变、卵巢手术史、放化疗以及子宫动脉栓塞术等。卵巢手术、放化疗以及子宫动脉栓塞术等破坏了卵巢血供，损伤了卵母细胞，导致卵巢间质纤维化或坏死，进而引起卵巢功能减退[48]。儿童期或青春期流行性腮腺炎、结核、痢疾杆菌、麻疹病毒、巨细胞病毒及人类免疫缺陷病毒感染等破坏了卵巢组织，使卵巢部分或全部功能丧失，引起卵巢储备功能降低，甚至卵巢功能不全[49]。

RWBSRO

(22)

与载客收益相比，用时较长的慢充带来的损失更大，同时为了减少排队用时，出租车仅快充且直接充满，充电时可用餐或休息，不参与放电，即出租车充放电行为不受电价影响。

根据北京市统计数据[21]，出租车载客间隔时间tj可拟合为对数正态分布lntj～N(2.156,1.5782)

2.2.3 公交车

公交车日行驶里程约为150～200 km，首班发车时间一般为05:30—06:30, 末班发车时间一般为20:00—21:00。每天上、下班时间(06:30—09:00, 16:30—18:30)为公交车运行高峰时段, 发车间隔一般为5～10 min, 所有车辆均参与运行, 其余时段发车间隔则较长, 约10～15 min。

电动公交车额定行驶里程约为250 km，充满电即可满足1天的需求，故选择结束运营后夜间慢充，不参与放电，即公交车充放电行为不受电价影响。公交车运载人数多，必须保证早班车发车前电池已充满，按照一车一桩标准配置专属慢充桩。

公交车按照制定好的规划行驶，行驶路线固定，时间变动也不大，不涉及不同区域之间的转移。

2.3 负荷计算

EV负荷计算考虑24 h，以1 min为单位时间，1天共有1 440个时间点。充电站i的负荷为

Pi(t)=Pi,c(t)-Pi,f(t)

(23)

3 最优网格划分

3.1 加权Voronoi图

Voronoi图由数学家M.G.Voronoi于1907年提出[22]，由1组距两相邻点距离相等线段组成的连续多边形构成。在此基础上，考虑不同生成元属性的不同赋予其不同权重，形成加权Voronoi图，可视为以各生成元为圆心向四周以不同速度扩散，扩散速度与权重成反比，可表示为

(24)

式中：P={p1,p2,…,pn}为生成元集合；d(x,pi)为点x距生成元pi的欧几里得距离；ωi为pi的权重，i≠j。

3.2 最优网格划分步骤

Step 1：以行政区域划分作为初始网格，在各网格内使用重心法得到初始站址；

Step 2：令t=1；

Step 3：t=t+1，并判断每辆EV在t时刻的状态，若恰好行程结束，则判断是否需要充电，若是，则将其作为充电需求点并记录负荷；

Step 4：若t=1 440，则转到Step 5，否则，转到Step 3；

Step 5：使用重心法在各网格内选择新的站址；

Step 6：计算新旧站址之间的距离，若小于阈值，则得到最优网格划分，否则，以新站址为生成元，以各网格内的总负荷为权重，重新生成网格，并转到Step 2。

4 算例与结果

仿真中私家车型号为比亚迪秦EV450，电池容量60.5 kW·h，最大续航400 km，快充功率60 kW，慢充功率10 kW，放电功率3 kW，Ⅰ类、Ⅱ类、Ⅲ类用户占比分别为10%、5%、85%。出租车型号为比亚迪e6，电池容量82 kW·h，最大续航400 km，快充功率60 kW。公交车型号比亚迪K9，电池容量324 kW·h，最大续航250 km，慢充功率为50 kW[23]。充电效率0.9，放电效率0.8。Smax=1，Smin=0.2，Tmax=10 min。在所有交通道路上每间隔10 m取一点作为候选站址，当重新选址后各充电站站址变化距离均小于100 m时，得到最优网格划分。

蒙特卡洛抽样次数为104次，其中私家车、出租车和公交车占比分别为94%、4%和2%。

仿真流程如图1所示。为简化计算，假设每段行程的起点和终点都为交通节点，若需要充放电，则本段行程的终点和下一段行程的起点变为充电站；假设出租车在载客间隔内不移动。

以某市40节点交通网络为例，分区、初始网格划分及初始站址分布如图2所示。每天07:00—9:00、11:00—13:00、17:00—19:00为上下班高峰期，考虑红绿灯等待情况，私家车和出租车高峰期行驶速度为30 km/h，其余时段速度为50 km/h，由于公交车运营中频繁停车，速度分别为15 km/h和30 km/h。

最优网格划分如图3所示，共设置了5个集中充电站。当放电电价为1.0元/(kW·h)、谷电充电价为0.4元/(kW·h)时，分别配备快充桩27、9、180、108、134个，慢充桩74、9、163、82、166个，放电设备50、31、682、446、363套，除此之外，由于夜间充电需求大，按照私家EV数量的80%在各小区内共设置慢充桩及放电设备7 520套，建设成本共计9 312.06万元。各网格均由最外侧矩形边界与网格交界线围成，用户位于网格内部及边界线上时，选择本网格内充电站。若用户需要充电时恰好在两网格交界处，考虑到用户前往充电站的路程，优先选择面积较小网格内的充电站。

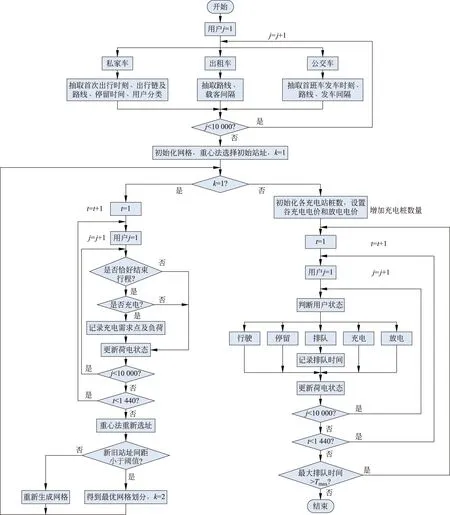
图1 考虑电价的充电服务网格划分及充电桩数量计算流程图Fig.1 Flow chart of charging service grid division and charging pile number calculation considering electricity price

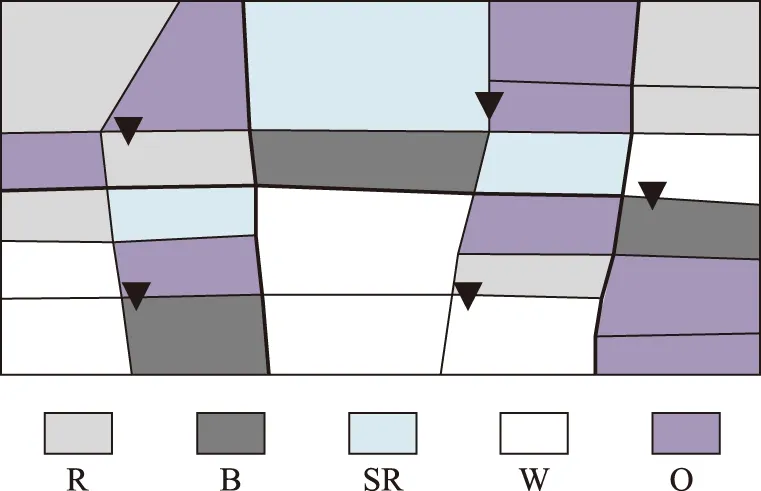
图2 四十节点交通网络Fig.2 Forty node traffic network

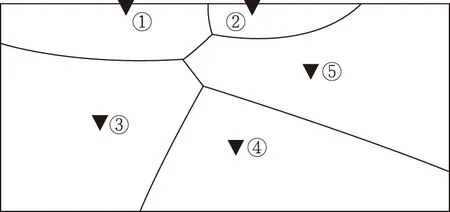
图3 最优网格划分Fig.3 Optimal grid division

此时，各充电站充电负荷如图4所示。5个集中充电站的负荷中各有2次短时间大功率用电，这是出租车集中在换班前快充导致，小区内个人慢充桩充电负荷集中在23:00到次日04:00。充电负荷小于0表示充电功率小于放电功率，当21：00放电价格降为0时放电功率也瞬间降为0，导致充电负荷瞬间升高，在充电站4、5和个人慢充桩表现明显。

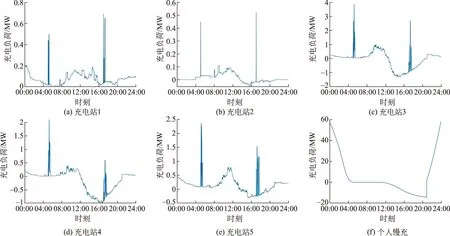
图4 各充电站负荷Fig.4 Load of each charging station

电力系统总负荷如图5所示。最小负荷以下的部分为基荷，由基荷机组承担，平均负荷以上的部分为峰荷，由峰荷机组承担，中间部分由腰荷机组承担。发电过程中，峰荷机组无法按照额定功率发电，且出力变化频繁，维护成本高，因此单位发电量成本最高，腰荷机组次之，基荷机组最低。假设基荷发电成本为0.3元/(kW·h)，腰荷成本0.5元/(kW·h)，峰荷成本1.0元/(kW·h)。不计及EV负荷时，发电成本207.8×104元，峰谷差占最大负荷的26.6%；EV不放电且无序充电时，发电成本212.5×104元，峰谷差增大，占最大负荷的28.2%；EV放电且部分有序充电时，发电成本207.9×104元，峰谷差占最大负荷的24.6%，电网运行成本降低4.6×104元。

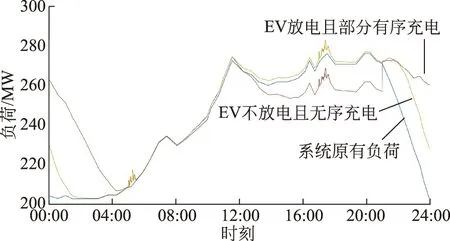
图5 电力系统总负荷Fig.5 Total load of power system

电网日运行成本的降低如图6所示。放电电价小于1.0元/(kW·h)时，日运行成本降低的程度随放电电价增大，大于1.0元/(kW·h)时变化不大。

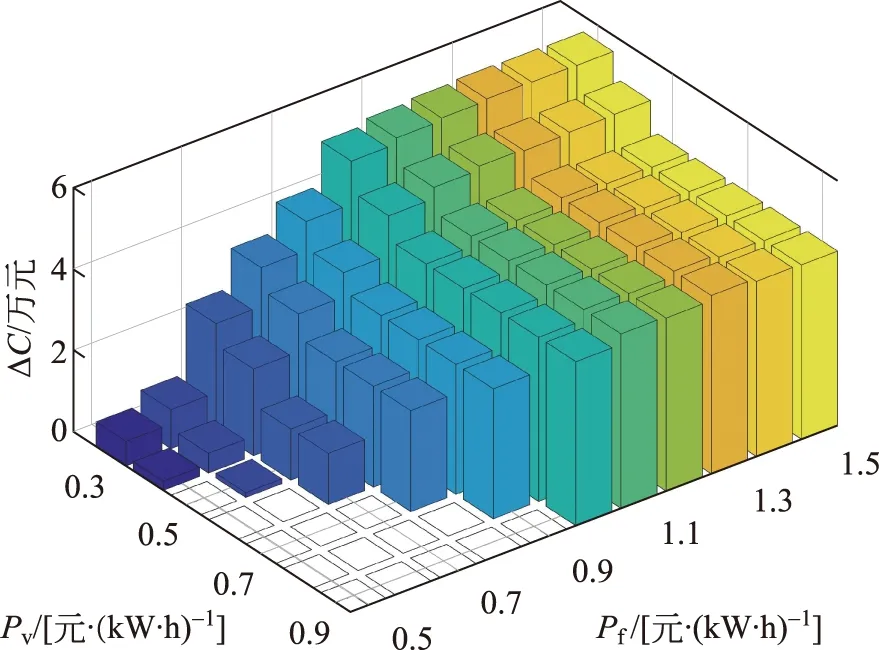
图6 电网日运行成本的降低Fig.6 Reduction of daily operation cost of power grid

谷电充电价小于0.5元/(kW·h)时，日运行成本降低的程度随谷电价增大而减小，大于0.5元/(kW·h)时变化不大。当放电电价为1.3元/(kW·h)，谷电价为0.3元/(kW·h)时，日运行成本降低最大，为5.62×104元。

用户日放电收益如图7所示，随着放电电价增大而增大，几乎不受谷充电电价影响。当放电电价为1.5元/(kW·h)时，日放电收益最大，为15.18×104元。

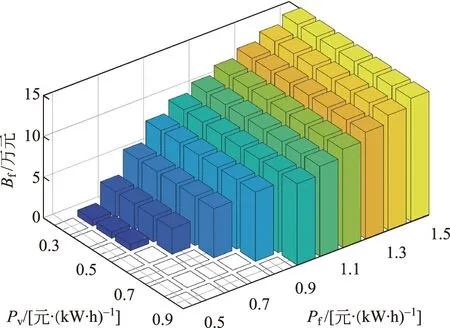
图7 用户日放电收益Fig.7 User daily discharge revenue

充电站日净收益如图8所示，为售电收益减去购电成本，随着谷充电电价增大而增大，几乎不受放电电价影响。当谷电充电价为0.9元/(kW·h)时，日净收益最大，为12.07×104元。

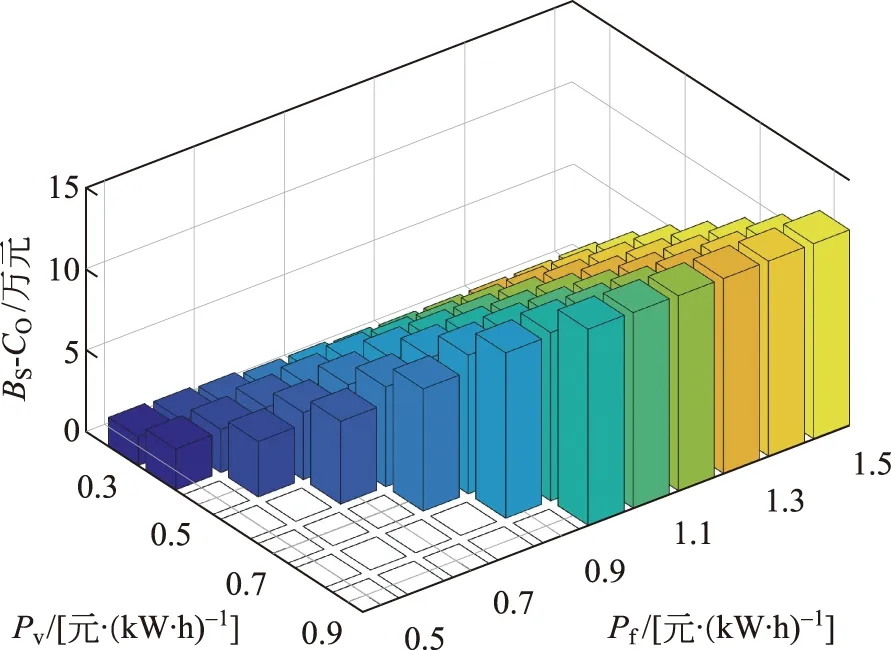
图8 充电站日净收益Fig.8 Daily net income of charging station

社会日总效益如图9所示，为电网日运行成本降低、用户日放电收益和充电站日售电收益三者之和。社会日总效益随放电电价和谷充电电价增大而增大，当放电电价为1.5 元/(kW·h)，谷充电电价为0.9 元/(kW·h)时，总效益最大，为42.20×104元。

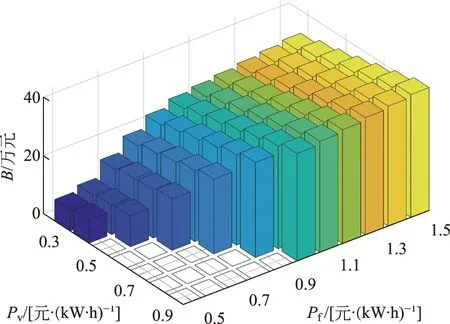
图9 社会日总效益Fig.9 Total social benefit per day

图10 总建设成本Fig.10 Total construction cost

总建设成本如图10所示。放电电价较低时，用户放电意愿低，不需要放电设备，建筑成本低。随着放电价格增大，参与放电的用户增多，需要更多的放电设备，建设成本小幅增加。建设成本几乎不受谷充电电价的影响。

在相同充放电价格及充电站站址不变的情况下，计算采用网格划分与不采用网格划分两种方案的经济性，结果如图11所示。不采用网格划分时，电网和用户收益下降，充电站和社会总效益基本持平，建设成本则明显上升。因此，采用网格划分经济性更好。

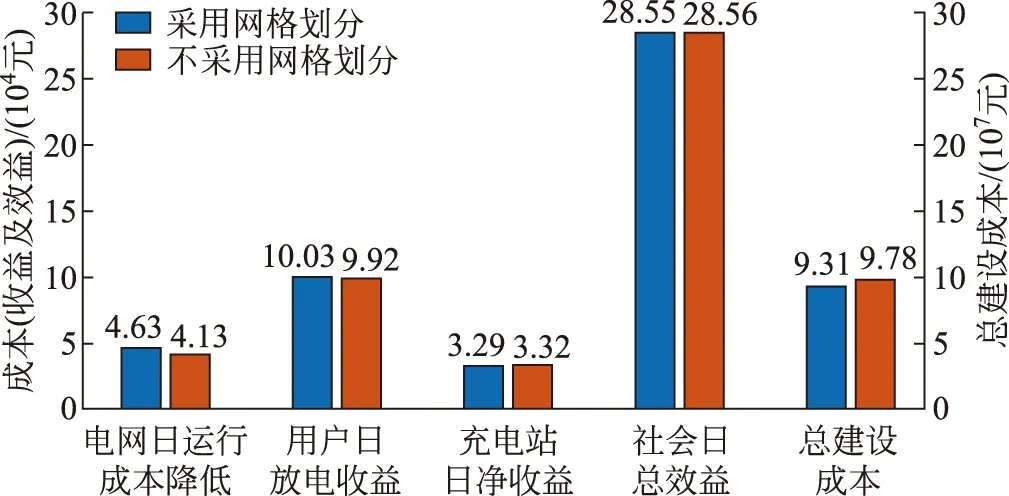
图11 两种方案对比Fig.11 Contrast the two schemes

5 结论

本文分析充电设施的经济性，考虑不同电价对充电负荷的影响，使用蒙特卡洛抽样结合Voronoi图原理进行最优网格划分。计算结果表明：(1)通过调整电价，可以引导用户放电和有序充电，在用户自身获益的同时，为电网降低峰谷差和运行成本，为充电站提供更高的经济效益；(2)当谷充电电价为0.3～0.9元/(kW·h)，放电电价为0.5～1.5元/(kW·h)时，电网日运行成本降低最大为5.62×104元，用户日放电收益最大为15.18×104元，充电站日净收益最大为12.07×104元，社会日总效益最大为42.20×104元。(3)采用网格划分具有更好的经济性。

文中未考虑出租车载客间隔内出行情况，可能导致出租车负荷计算不够准确。后续研究工作将着眼于配电网研究，在充电网和配电网协同规划的基础上进行网格划分，更具有应用价值。