基于正态分布的典型负荷日拟合方法

2020-09-21韩宏志马勤勇赵建平袁铁江

分布式能源 2020年4期

韩宏志，杨洋，郜宁，马勤勇，赵建平，袁铁江

(1.国网新疆电力有限公司电力科学研究院，新疆乌鲁木齐 830011；2.大连理工大学电气工程学院，辽宁大连 116024)

0 引言

风电大规模接入使得电网调峰能力不足，引发大量弃风现象[1]。为保证电力系统稳定，需要对风电出力进行预测以及增加储能配置。进行电力系统负荷预测、储能容量配置、电网调度等工作都需要选取合适的典型负荷日。目前，典型负荷日选取没有统一的方法，一般选峰谷差最大、最大负荷最大的曲线作为典型负荷日曲线。近年来对典型负荷日选取的研究有很多，并取得了一系列成果。文献[2]对比分析典型负荷日特征与年最大负荷代表月份的日负荷特性，根据广东电网负荷变化的实际情况，从电网调峰需求的角度出发，提出将夏季典型日分为典型工作日和双休后典型日。文献[3]将典型日负荷曲线的选取问题转化为基于统计学习的多元分类问题,利用概率潜在语义分析模型进行问题求解。文献[4]提出了基于自适应因子与概率统计法相结合的改进模糊聚类算法典型日负荷曲线选取新方法,应用日负荷率、日负荷波动率等描述性特征指标,确定最优聚类数;引入模糊-离散系数,辨识样本数据中的畸变日,并予以剔除;计算日负荷与月平均负荷之间的相关系数,依据相关系数选取典型日负荷曲线。文献[5]提出一种基于反一致自适应聚类的典型日选取方法，通过反一致自适应可能性C均值聚类算法求取典型日负荷曲线,然后利用样条插值修正典型日负荷曲线。目前多采用聚类算法去除畸变数据[6]，但是聚类算法具有聚类中心、聚类数目难以确定的缺点。文献[7]提出一种基于AP聚类的远景年典型日负荷预测方法，首先，选取历史日负荷数据，并进行标幺化处理；其次，基于AP聚类算法对历史日负荷数据进行聚类，以此作为远景年的负荷特征；最后，基于远景年负荷的预测值，并结合聚类后的负荷特征，计算出远景年典型日负荷曲线。文献[8]针对智能电网建设过程中需准确选择能够代表季节负荷特性典型日的要求，提出了一种计及温度区间的典型日筛选方法。在对负荷影响因素和日负荷曲线聚类分析的基础上,根据温度区间对日负荷重新分类,利用加权重心法筛选出每一类的典型日。文献[9]针对微电网中典型日选取问题，综合考虑资源和负荷总量特征、分布特征、典型性和极端性，构建了典型日选取综合评估指标体系，结合混合整形多目标线性优化建立了典型日选取模型。文献[10]通过对历史数据的预处理、初始聚类中心的设置以及最优聚类数目的确定,建立典型日负荷曲线的聚类预测模型。文献[11]针对典型负荷日选取误差，提出采用两阶段模糊规划分配典型日权重方法,减小了典型日与原始数据间的误差。文献[12]采用选取2个特定日的统调负荷曲线相减得到差值曲线并对其进行修正的方法,近似模拟出分布式光伏电源典型日曲线。文献[13]提出了一种多窗口宽度的主导间谐波频谱分布的算法,该算法能够简单、快捷和准确地计算主导间谐波频谱分布，对典型负荷日的频谱分析提供了借鉴。文献[14]根据日负荷分类标幺化曲线和比例系数得到配变的实际日负荷标幺化曲线，利用配变的实际日负荷标幺化曲线和配变的实际日用电量形成配变的实际日负荷曲线,得到配变的实际日负荷有功功率曲线和无功功率曲线。

以上文献都只考虑了选取已有1天的负荷数据，而已有的数据往往不能反应出负荷日的最典型特征。本文通过大量的电网负荷数据，提出将不同负荷日同一时刻的负荷数据拟合成正态分布曲线，然后利用该分布曲线的期望作为该时刻的负荷值拟合典型负荷日曲线的方法。

1 基于正态分布的典型负荷日拟合方法

1.1 正态分布概述

正态分布模型是一种在工程领域中经常用到的概率分布模型。正态分布又称为高斯分布，其函数图像称为正态曲线。

若随机变量Z的概率密度曲线是

(1)

式中：σ>0，且μ，σ都是常数，称随机变量z服从参数为μ，σ2的正态分布，记作Z～N(μ，σ2)。

若要将随机变量拟合为正态分布，只需确定μ和σ2即可，其中μ为该分布的期望，σ2为该分布的方差。

1.2 典型负荷日拟合方法

将1天按1 h为1个时段，分为24个时段，然后利用大量的电网负荷数据，将不同天的各同一时刻负荷数据拟合成正态分布，最后将各时刻正态分布的期望作为典型日该时刻的负荷值。通过计算24个时段的负荷值得到最终所拟合的典型日。

利用各个时刻负荷值出现的频率表示该负荷值出现的概率，其具体计算如下

(2)

式中：pij表示第j天中第i个时段负荷出现的概率，i=1, 2, …,24；mij表示第j天中第i个时段负荷在整个数据中第i时段出现的次数；n表示数据包含的总天数。

然后，利用最大似然估计法将不同天同一时刻的负荷数据拟合成正态分布。通过式(2)得到负荷值与其出现的概率组合(qij,pij)，为方便应用最大似然估计法将(qij,pij)去掉重复数据后表示为(xia,yia)。其中，qij表示第j天中第i个时段的负荷值；xia表示不同天同一时段去掉重复数据后所剩余的负荷值，yia表示xia出现的概率。

假设第i个时段有bi个重复数据，那么

a=1,2,…,n-bi

(3)

式中：a表示i时刻样本中的第a个负荷值；bi表示i时段重复负荷值的个数。

为计算第i个时段正态分布的参数，将xia当作总体的样本，似然函数L(θi)为

(4)

式中θi为要估计的未知量。

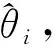
(5)

通过最大似然估计法求得第i时段的正态分布函数后，利用下式求第i个时段负荷值的期望

(6)

式中：E(xi)表示第i个时段的期望；xi表示第i个时段正态分布函数的自变量。

将此期望值作为该时刻的负荷值，计算所有时刻的期望后，利用这些期望拟合成典型负荷日，即将E(x1),E(x2),…,E(x24)作为所拟合的典型负荷日的负荷值。

2 典型负荷日拟合评价指标

利用日负荷率与数据平均日负荷率之差的绝对值作为评价指标1，将选取的典型负荷日与数据所有负荷日相关系数绝对值的平均值作为评价指标2，来评价典型负荷日拟合效果。

2.1 评价指标1

日负荷率是日平均负荷与日最大负荷的比值，用来描述日负荷曲线，表征1天中负荷分布的不均衡性，即

(7)

式中：γj表示第j天的日负荷率；qij为第j天中第i个时段的负荷值。

指标1的计算方法为

(8)

式中：z1表示指标1；γd表示选取的典型负荷日的负荷率。

2.2 评价指标2

皮尔森相关系数[15]能够很好的描述2组数据的相关性，设存在2数组X、Y，当r>0且系数越大，那么这2组数据的正相关性越强，当r<0且系数越小，那么这2组数据的负相关性越强。相关系数r为

(9)

式中：r为相关系数；X=[x1,x2,…,xm],Y=[y1,y2,…,ym]为2个数组，m为数组中元素的个数。

典型负荷日与数据所有负荷日相关系数绝对值的平均值作为指标2，指标2计算方法为

(10)

式中：z2表示指标2；γj表示典型负荷日与第j天的相关系数。

指标2越大，表示所选取的典型负荷日与其他天数的负荷相关性越强，则选择的典型负荷日越好。

3 算例分析

3.1 算例简介

新疆和田地区冬季供热机组多，供热负荷大，每天最大负荷接近，应用传统方法难以选出最有代表性的典型负荷日。为验证该典型负荷日拟合方法的优越性，选取和田地区冬季的负荷数据以1 h为1个采样点，每天采样点数为24，应用Matlab软件编写程序进行仿真实验。

3.2 算例结果及分析

利用最大似然估计法将不同天同一时刻的负荷数据进行正态分布拟合置信度为5%，拟合结果如表1所示。

表1是24个时点利用最大似然估计法拟合成正态分布的结果表，将其中各个时刻的期望作为拟合典型负荷日的负荷值得到最终的典型负荷日，其图像如图1所示。

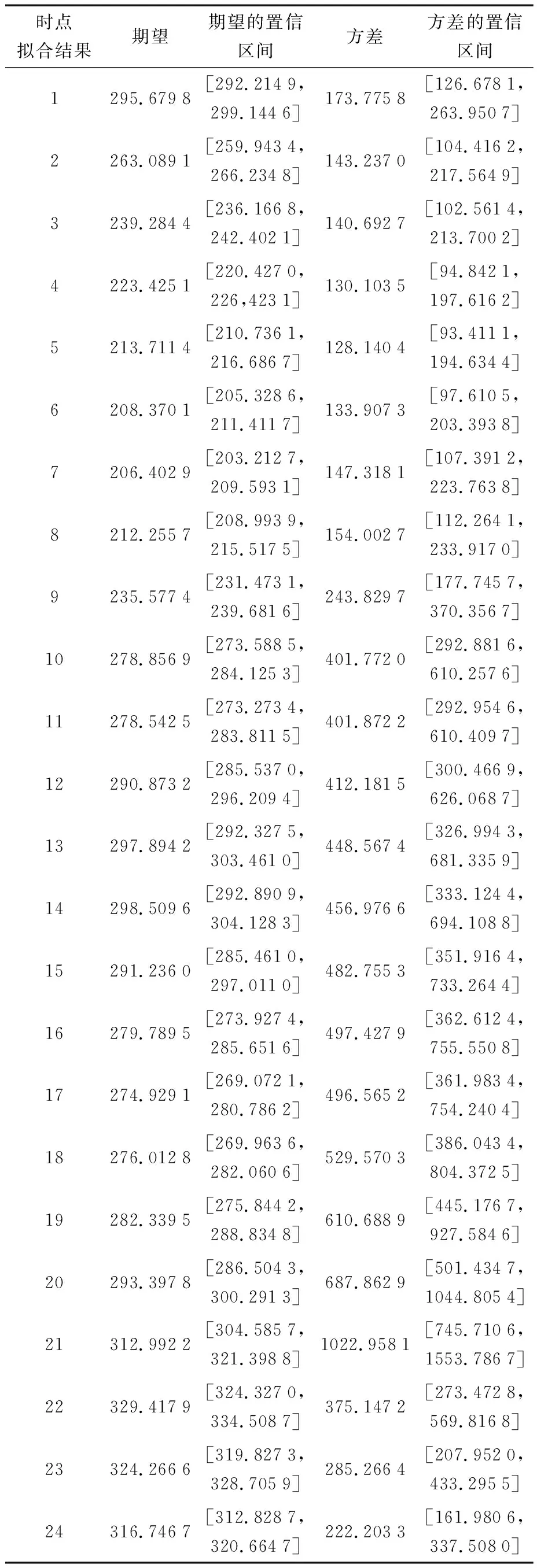
表1 拟合结果Table 1 Fitting results

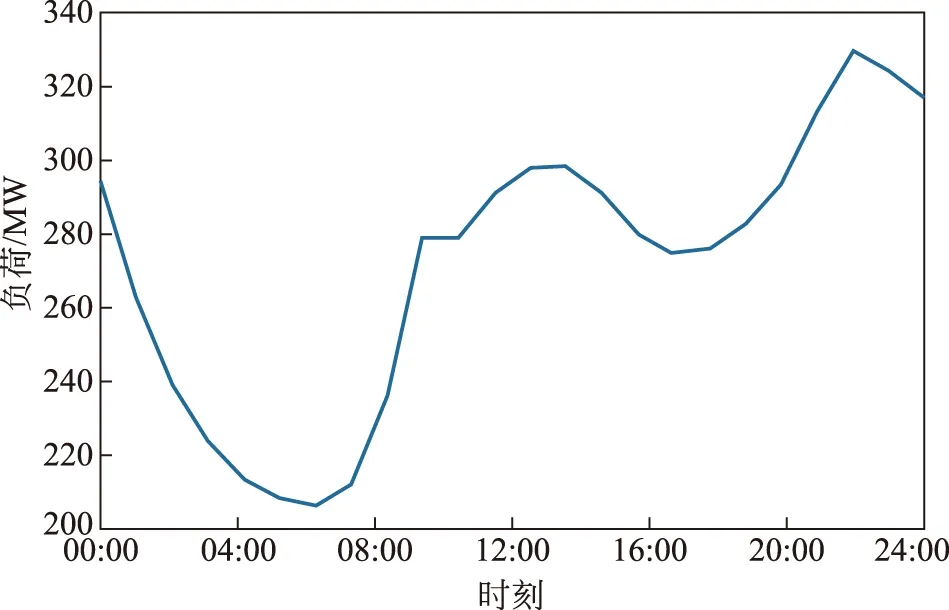
图1 所拟合的典型负荷日曲线Fig.1 Typical load daily curve fitted

为了体现该拟合方法的优越性，用传统方法选取最大负荷最大日和峰谷差最大日作为典型负荷日与该方法所拟合的典型负荷日进行比较，负荷图像如图2所示。

图2 典型负荷日曲线Fig.2 Typical daily load curve

计算传统方法与本文所提方法选取的典型负荷日的指标，结果如表2所示。

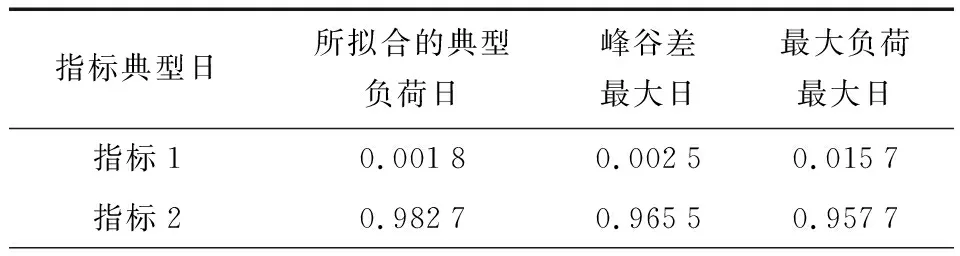
表2 典型负荷日评价指标Table 2 Daily evaluation indexes of typical load

表2为典型负荷日的评价结果表，由表2可以看出由本文所提方法选取的典型负荷日指标1比传统方法选取的典型负荷日低，指标2比传统方法选取的典型负荷日高。由前文所述，指标1表示日负荷率与数据平均日负荷率之差的绝对值，指标1反应了所选取的典型负荷日的日负荷率与数据平均水平的差距，其值越小则典型负荷日选取的越典型；指标2表示典型负荷日与数据所有负荷日相关系数绝对值的平均值，指标2越大表示所选取的典型负荷日与其他天数的负荷相关性越强，则选择的典型负荷日越好。