电力变压器故障诊断的k值自适应加权KNN算法研究

2020-09-21张彼德

湖北电力 2020年2期

张彼德，梅婷，王涛

（西华大学电气与电子信息学院，四川成都610039）

0 引言

作为电力系统中最为核心的设备，电力变压器对整个系统的安全稳定运行起着举足轻重的作用［1］。因此，有必要对变压器的运行状态进行监控，及时诊断出变压器的潜伏性故障，解决系统安全隐患［2］。在变压器故障诊断技术之中，油中溶解气体分析（Dissolved Gas Analysis，DGA）是最为有效也最常用的一种［3］。DGA 技术实时性强，效果直观，且对于发现变压器内部潜伏性故障具有显著效果，已成为变压器故障诊断中最为方便有效的方法之一［4-5］。近年来，人工智能在变压器故障诊断领域得到了广泛应用，各分类模型也发挥了良好的分类效果。常用的分类模型有k 近邻（K-Nearest Neighbor，KNN）［6-8］、人工神经网络（ANN）［9-11］、支持向量机（SVM）［12-14］、贝叶斯网络［15-17］、模糊理论［18-19］等，其中，KNN算法由于其简单有效、易于实现、适用性强等特点而得到了广泛研究。

KNN 算法是由Cover 等人提出的经典分类算法之一，被广泛应用于文本分类［20-21］、人脸识别［22-23］、故障诊断［24-25］等领域之中。传统KNN 算法首先寻找训练样本中与待测样本距离最近的k 个样本点，并统计所有近邻样本的类别，最后将出现次数最多的类别作为待测样本的类别。然而，传统KNN算法也有一些不足之处，主要包括以下几个方面。首先，KNN 作为一种懒惰算法，在特征维数较高时会使得计算量较大；其次，近邻个数k 为固定取值，在实际应用中k 值难以确定，且在样本分布不均时对k进行固定取值并不科学；并且，KNN算法在判定待测样本类别时对所有近邻点施加相同的权重，未考虑样本分布带来的影响。针对上述问题，一些学者从不同角度提出了相关的改进方法。Hui-Ya Li 等［26］提出了一种应用于模式识别领域的快速KNN算法，通过在小波域中进行局部距离搜索来寻找距待测样本点最近的k 个训练样本，实验结果表明该方法可有效缩短KNN 的运算时间。Bhattacharya等［27］针对数据分布不平衡的情况，对不同k值下得到的结果进行了比较分析，提出了k值的选择策略，并经UCI数据集验证了可行性，但该方法仍是采用固定k 值。Sun 等［28］提出了一种k 值自适应选择方法，选用待测样本点最近邻样本的近邻数作为待测样本的k值，该方法简单直接，但未考虑到样本分布情况与异常点等问题，使用范围较为受限。

本文针对变压器故障数据特点，对KNN算法从以下几个方面进行了改进：1）由于变压器样本分布较广，且常有数值异常的离群样本出现，为减小离群样本对分类结果的干扰，对样本数据的局部异常因子进行计算，并以此为根据对离群样本进行剔除；2）考虑样本分布情况，根据待测样本的近邻点密度对k 值进行自适应选择；3）在判断待测样本所属类别时，综合考虑待测样本与近邻点间的欧氏距离，以及待测样本与各类别样本的分布相似度，对权值进行了重新定义。

1 传统KNN算法

KNN算法是由最近邻规则延伸得到的，不同于最近邻法，KNN算法将用于决策的近邻点从一个拓展为k 个，从而获得更多有效信息用于最终的决策［29］。相比其他分类算法，KNN 算法省略了学习的过程，分类原理简单直接，且对大部分分类问题都具有良好效果。

传统KNN算法流程如下：

1）输入训练样本集X=｛X1，X2，…，Xm｝，m 为训练样本个数，并设定k值；

2）输入测试样本集T=｛T1，T2，…，Tn｝，n为待测样本个数，并对测试集中的每一个待测样本点Ti，计算其与训练集中每个样本点Xi间的距离；

3）选择距离待测样本Ti最近的k 个训练样本点，作为该待测样本的近邻集合kNNTi；

4）统计集合kNNTi中所有训练样本的所属类别，并将待测样本点划分为出现概率最大的类别。

5）重复步骤3）和4），直至测试样本集的所有样本点划分完毕。

由以上步骤可以看出，传统KNN算法的近邻个数k为固定取值，且在划分待测样本点所属类别时，认为所有近邻点具有相同的重要程度。而在实际应用中，固定k 值与等权重无法适应不同分布的样本数据，容易对分类结果造成不利影响。

2 k值自适应加权KNN算法

为使KNN 算法中的k 值适应数据分布，且在分类时综合考量各近邻点重要程度，本文根据局部数据密度对k 进行自适应取值，并结合欧式距离与分布相似度，对各近邻点进行加权处理，以使最终的分类结果更加合理。

2.1 离群点检测

由于KNN 算法的分类依据是待测样本近邻点的所属类别，若近邻点中包含离群数据，将对结果造成不利影响。因此，有必要对样本数据进行离群点检测，剔除明显离群样本，减小对分类结果的干扰。本文通过计算每个样本点的局部异常因子来检测离群样本［30］，基本原理如下。

设数据集D 中点p 与第k 个近邻点的距离为dk（p），并根据此距离建立点p 的近邻合集Nk（p），即Nk（p）中所有数据点与点p间的距离≤dk（p），Nk（p）称为点p的第k距离邻域，表示为

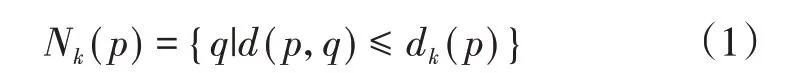
式（1）中d（p，q）为数据点p和q间的距离。若d(p，q) ＞dk(p)，则点p和点q之间的可达距离定义为d（p，q）；若d(p，q) ≤dk(p)，可达距离定义为dk（p），即

根据数据点的可达距离计算局部可达密度，并以此作为该数据点的相对密度，局部可达密度按式（3）计算：

式（3）中，lrdk(p)表示点p的局部可达密度，其值越大，则点p 与其近邻点为同类点的可能性越大；反之，点p是离群点的可能性越大。

为进一步表示出点p 离群的可能性，定义局部异常因子LOFk（p），即点p第k距离邻域Nk（p）的局部可达密度与点p的局部可达密度之比的平均值。

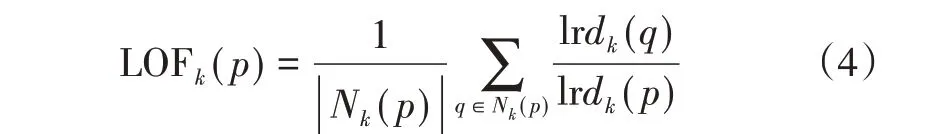
若该值越接近于1，说明点p 与其邻域点密度相近；若该值小于1，说明点p处的密度大于邻域点密度；若该值大于1，说明点p 处的密度小于邻域点密度，即该值越大，点p为离群点的可能性越大。

2.2 基于局部密度的自适应k值

针对传统KNN 方法中k 值为固定取值，无法适应数据分布的缺点，本文根据数据的局部密度对k 值进行选取，使k的取值能适应数据分布实现自适应取值。为便于分类，k值通常取奇数值，且为避免最近邻点的干扰以及减小计算复杂度，将k 值的范围限定于区间［3，15］内。

设k 为待测样本的近邻个数，d 为待测样本到第k个近邻样本的距离，定义样本局部密度ρ 为单位面积上近邻样本的个数。

对k在限定区间内进行取值，并记录不同k值下局部密度的大小，若密度越大，表示k 值可信度越高，最终取密度最大时的k 值作为该待测样本点的近邻个数k。

2.3 近邻点加权

传统KNN算法对待测样本进行分类时，认为所有近邻点具有相同的重要程度，但这种做法并不合理。例如，取一种极端情况，让待测样本的近邻数等于训练样本总数，此时待测样本将被直接归为样本个数最多的那一类。将待测样本近邻点的分布情况纳入分类决策中，即对近邻点进行加权处理，则能有效避免这种情况的出现。

最常用的加权方式是采用待测样本到近邻点间距离的倒数作为权重，计算方式如下

式（6）中：D为待测样本到近邻点间的距离；C为一个常数，避免距离很小时权重值过大。

距离倒数加权方式方便快捷，但存在较近样本权值过大，由近至远时权值衰减过快等问题。本文的加权方式主要从以下两个方面来考虑：

1）根据待测样本到近邻点间的距离，采用高斯函数进行加权，对权值变化进行平缓过渡处理，公式如下

式（7）中，a 取1，C 取0.5。由以上公式可以看出，当近邻点与待测样本距离为0 时，权值为1；随着距离的增大，权值平缓衰减，且永不为0。

2）若取待测样本近邻数为k，则会选取距待测样本最近的k个点作为其近邻点，而这k个近邻点可能来自不同类别，属于同一类别的近邻点称为“同一类别近邻点”。通常，不同类别的数据点具有不同的分布规律，在加权时还应对待测样本点与各类别样本数据的分布相似度进行考虑。本文通过计算各类别近邻点的近邻平均距离，并与待测样本点距该类别近邻点的平均距离相比较，来评价待测样本与该类别数据的分布相似度，从而进行加权。两者分布越相似，证明待测样本点属于该类别的可能性越大，相应赋予该类别近邻点的权值也越大。

①遍历待测样本xi的近邻点类别标签，记录各类别近邻点数量Nc，并以xi的近邻个数ki作为其近邻点的近邻个数，计算各近邻点与其邻域点间的近邻平均距离。第c类近邻点的近邻平均距离计算公式如下

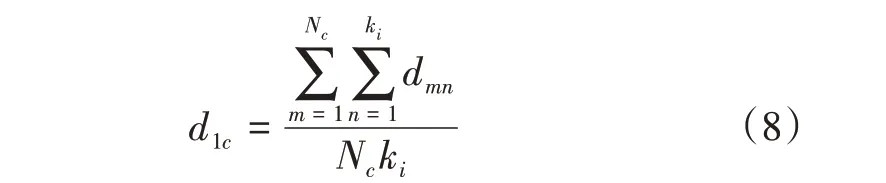
式（8）中：Nc为类别c 的近邻点数量；dmn为待测样本类别c的近邻点m与其邻域点n之间的距离。

②计算待测样本点与第c类近邻点间的平均距离

式（9）中dj为近邻点j到待测样本间的距离。

③根据近邻平均距离及待测样本与其近邻点间的平均距离，对类别为c的近邻点权值进行计算，

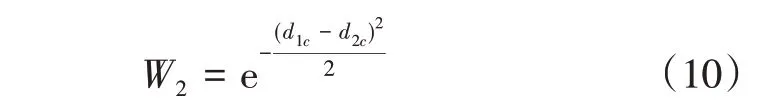
从式（10）可以看出，当距离d1c与d2c相同时，表示待测样本与第c类近邻点分布相同，则第c类近邻点的权重值为1；若两个距离值相差越大，说明待测样本与第c类近邻点分布差距越大，权值则越小。

本文从以上两个方面对加权方式进行了综合考虑，并定义每个近邻点的权值为

式（11）中：W1为根据近邻点到待测样本的欧式距离得到的权值；W2为根据待测样本与各类别样本数据的分布相似度得到的权值，二者的结合能更准确地反映各近邻点的重要程度，从而合理确定权值。

3 基于k 值自适应加权KNN 算法的变压器故障诊断

3.1 样本数据收集及故障类型划分

变压器结构复杂，故障类型繁多，但主要可分为过热型故障与放电型故障。本文参考IEC60599标准，将故障类型划分为以下5种：中低温过热（T12）、高温过热（T3）、局部放电（PD）、低能放电（D1）与高能放电（D2）。本文从已发表文献中收集了DGA 数据433 组，具体如表1所示。

表1 故障样本数据组成Table 1 Composition of the fault data

3.2 特征量选取与数据预处理

1）特征量选取

电力变压器内的绝缘油和绝缘材料在电和热的作用下，会逐渐老化分解并产生气体，并溶解于绝缘油之中。这些气体主要包括H2、CH4、C2H4、C2H6、C2H2、CO、CO2、O2、N2等，由于CO、CO2、O2、N2等气体分散性大且获取不易，因此通常并未列入故障诊断特征气体中。本文选取H2、CH4、C2H4、C2H6、C2H2五种气体的体积分数作为输入特征量。

2）数据预处理

由于变压器数据值分布较广，甚至在数量级上具有显著差异，因此为避免数据值差异过大，影响模型的稳定性与收敛性，通常会对原始数据进行预处理。常用的数据预处理方法有离差归一化（MMN）、标准差标准化（ZSN）和反正切函数转换（ATAN）等。

MMN和ZSN方法属于线性预处理方法，将原始数据进行缩放，并落入指定空间内。但线性方法无法缩小数据间的数量级差异，且通常将各特征进行单独映射，未考虑特征之间的横向联系，会使原始数据丢失一部分有价值信息。ATAN方法通过反正切函数实现对数据的预处理，由反正切函数特点可知，在数据分布较广时，易导致预处理后的数据大量集中于边界处，使得数据分布不均。通过以上分析可知，上述几种方法都不适用于数据分布不均，且数值分布较广的变压器故障数据。

对数变换方法能缩小原始数据在数量级上的差异，使得数据分布更加紧凑，同时其对数据进行整体映射，能合理保留数据特征。因此，本文采用对数变换对数据进行预处理，

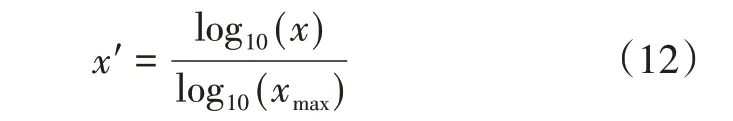
式（12）中xmax为样本数据的最大值。

3.3 变压器故障诊断步骤

将本文提出的k值自适应加权KNN方法用于变压器故障诊断之中，建立故障诊断模型，具体步骤如下：

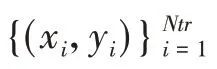
2）对归一化后的训练样本数据进行离群样本检测，并剔除明显离群样本；

3）根据样本的局部密度，按照式（7）对k值进行自适应取值；

4）对各近邻点与待测样本间的距离，以及待测样本与近邻点分布间的关系进行综合考虑，根据式（7）～（11）对近邻点权值进行计算；

5）统计待测样本点各近邻点类别，计算各类别近邻点的总权重，并以最大权重为原则对待测样本进行分类。

4 实例分析

4.1 离群点剔除

对训练样本按类别进行离群点检测，得到的局部异常因子分布情况如图1所示。

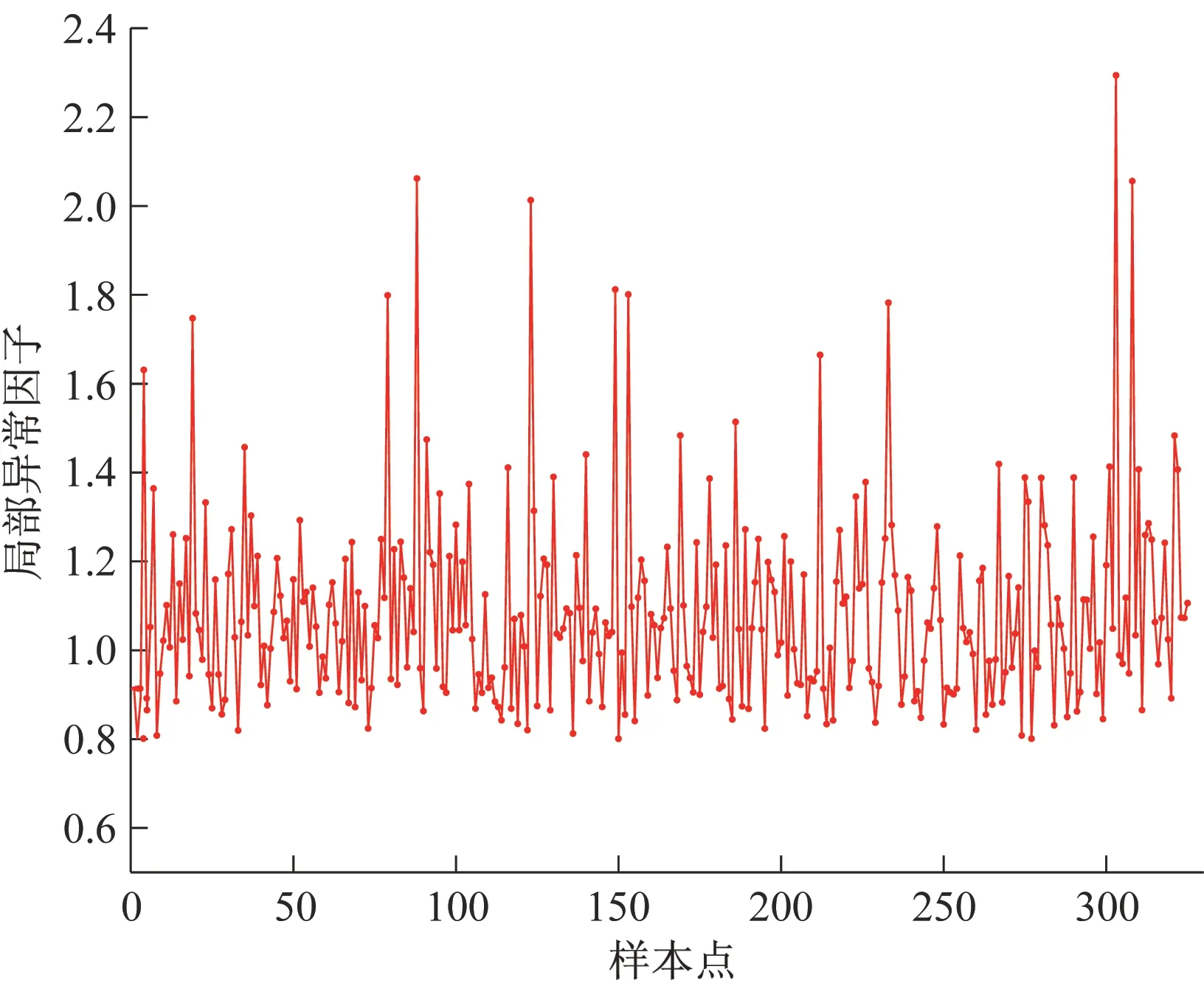
图1 局部异常因子分布情况Fig.1 Local outlier factor distribution

从图1可以看出，样本点的局部异常因子值通常在1附近波动，但在某些“异常点”处波动较大，本文取阈值为1.5，剔除原始数据中的12个“异常点”，即离群点。

为直接观察样本点分布情况，对训练样本数据进行主成分分析，选取第一主成分PCA1 与第二主成分PCA2，分别作为横坐标和纵坐标，并在图中标示出原始数据中判断为异常点的数据点，得到的离群样本分布图如图2所示。

图2 离群数据分布情况Fig.2 Outlier data distribution

经数据可视化后可以看出，所剔除的异常点大部分都明显离群，对其进行剔除后有利于最后的分类工作。

4.2 自适应k值

根据本文方法对k 进行自适应取值，记录各待测样本点所选取的k值，绘制折线图如图3所示。

从图3可以看出，本文提出的根据局部密度方法，可以在考虑样本分布的情况下实现对k 的自适应取值。

图3 k自适应取值Fig.3 Adaptive value of k

4.3 故障诊断结果及对比

基于相同的训练集与测试集，将样本数据按式（12）进行归一化之后，分别输入到BPNN、SVM、传统KNN以及本文改进得到的KNN分类器中进行分类，并与改良三比值法的分类效果进行对比，结果如图4所示。

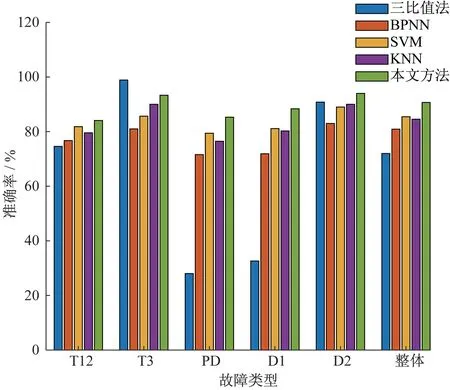
图4 故障诊断结果Fig.4 Fault diagnosis result

从图4 结果可以看出，改良三比值法的整体诊断准确率虽能达到72%，但其局部放电（PD）和低能放电（D1）的诊断准确率仅有28%和32.61%，效果较差。与改良三比值法相比，四种智能分类方法的诊断准确率更高，且不同类型故障的诊断准确率未出现较大差异，具有更好的诊断效果。并且，相较于BPNN、SVM和传统KNN三种分类器，无论是单个故障还是整体的诊断准确率，本文方法所得结果都更优。其中，BPNN、SVM、KNN 和本文方法所得到的整体故障诊断准确率分别为79.6%、85.2%、84.3%和91.7%，说明本文方法能对变压器故障类型进行更为有效的划分。