3300 hp五缸压裂泵曲轴连续梁法和有限元分析强度计算对比*

白尚懿,刘文宝,路海龙,张天临

(1.兰州兰石石油装备工程股份有限公司，甘肃 兰州 730314；2.机械工业油气钻井装备工程技术研究中心，甘肃 兰州 730314；3.甘肃省油气钻采装备工程研究中心，甘肃 兰州 730314)

0 引 言

压裂泵在压裂作业过程中起着至关重要的作用，而曲轴是压裂泵动力端中非常关键的零部件，在压裂泵运行过程中，曲轴将输入扭矩通过连杆传递给十字头体，进而传递给柱塞，而柱塞承受着压裂液的交变压力。因此，曲轴承受输入转矩、轴承座支反力、液力端传递到连杆作用力等多种载荷作用[1]。随着超高压井和超深井的出现及快速发展，对压裂泵提出了更高的要求。因此，对压裂泵曲轴的结构进行强度分析，得到其应力分布情况，对于其科学设计是非常必要的。目前，压裂泵曲轴强度分析一般只采用有限元方法进行[2-5]，而鲜有人将连续梁法和有限元分析方法结合起来进行对比计算。

笔者以输入功率为3300 hp的五缸压裂泵为例，首先采用连续梁法对曲轴进行强度计算，然后基于Simulation对压裂泵曲轴进行有限元分析，通过两种方法的对比计算，为压裂泵曲轴的科学设计提供理论依据。

1 曲轴连杆机构运动学及动力学分析

1.1 运动学分析

曲柄连杆机构的运动规律如图1所示，其中，e为曲柄半径，L为连杆长度，λ为连杆比，λ=e/L，十字头体的位移表示为x，具体计算如下：

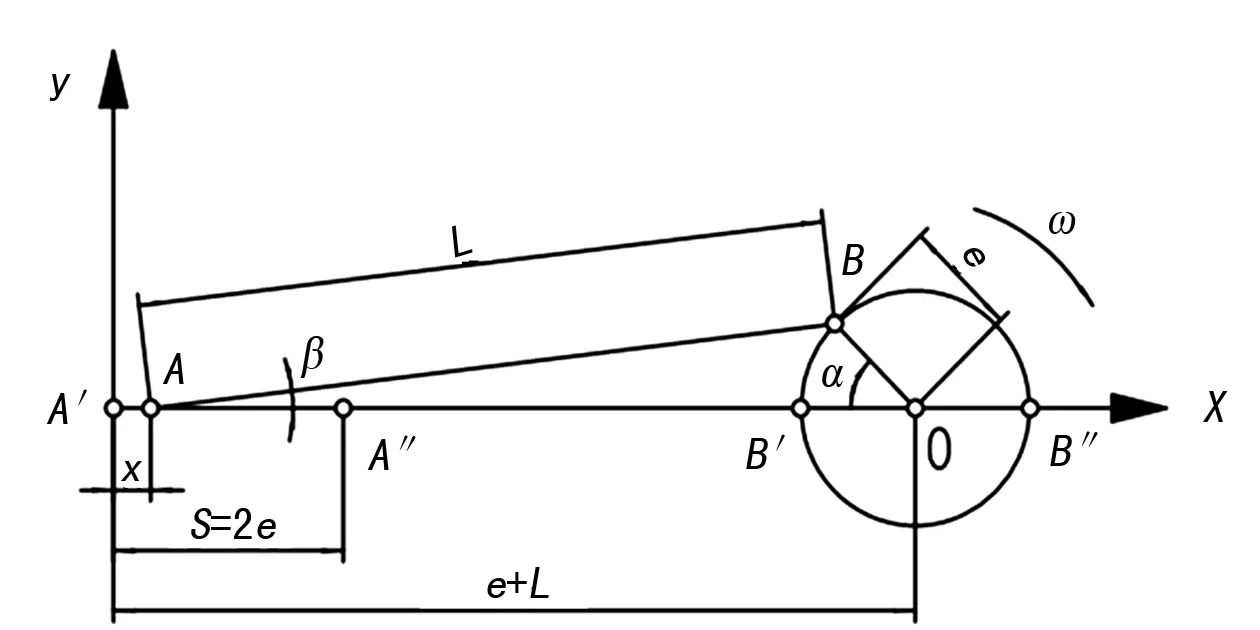
图1 曲轴连杆简图

x=A′A=A′O-AO

=(e+L)-(Lcosβ+ecosα)

在△AOB中，利用正弦定理，有：

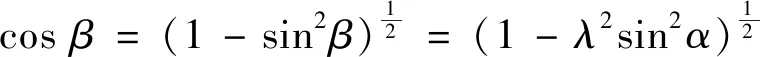
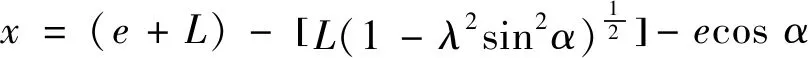
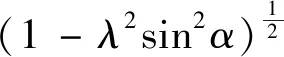
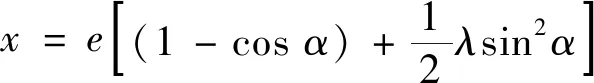
对x求两次导数得到柱塞速度和加速度：

a=eω2(cosα+λcos 2α)

式中：ω为曲柄旋转角速度。

1.2 动力学分析

1.2.1 小连杆上的作用力

如图1所示的曲轴连杆模型，在连杆绕支座作顺时针转动时，小连杆上的拉力或者压力依据柱塞处于吸入过程或者排出过程，按照不同的计算公式计算。α=0°～180°是吸入过程，α=180°～360°是排出过程。

(1) 吸入过程

当α=0°～180°时，系统处于吸入过程，小连杆上所受的作用力为：

式中：a为作用在盘根上的径向压力系数；μ1为柱塞与盘根间摩擦系数；l为盘根长度；D为柱塞直径；p为吸入过程时，柱塞只承受大气压力，0.1 MPa。

(2) 排出过程

当α=180°～360°时，系统处于排出过程，小连杆上所受的作用力为：

式中：P为液体压力，140 MPa。

1.2.2 往复部件的惯性力

在连杆往复运动的过程中，所有部件都会产生水平方向的惯性力。下面公式用于计算往复运动部件在水平方向的惯性力。

Ig=mpeω2(cosα+λcos 2α)

式中：Ig为往复部件的惯性力；mp为往复组件的总质量。

1.2.3 十字头上所受的水平力

十字头上的水平力等于小连杆上的水平力，与摩擦力，还有惯性力的和，即：

F=FXL+Gf-Nf+Ig

=FXL+Gf-F|tanβ|f+Ig

所以，十字头的水平力为：

式中：G为十字头总成的质量；f为摩擦系数；N为十字头在滑道上的正压力。

N=Ftanβ

1.2.4 各连杆上承受的作用力

按照图2所示力的分解方法，十字头上的水平力F与连杆力Q之间存在如下关系：

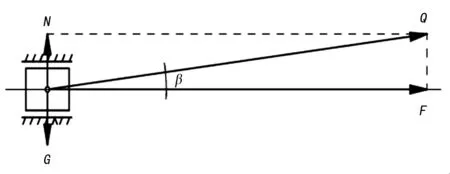
图2 十字头上力的分解示意图

在曲柄转动过程中，连杆方位不断变化，所以，上式中的β不断变化。需要利用连杆和曲柄之间的几何关系式确定两者的关系。

进一步地，可以求出曲柄上的径向力R、圆周力T、水平分力Qx与垂直分力Qy。

2 连续梁法曲轴强度计算

根据压裂泵的使用情况和大量试验研究分析，压裂泵曲轴实际是静不定的多支撑空间连续梁，支座弯矩影响曲轴应力状态。连续梁法即将曲轴简化为刚度阶梯变化的多支撑当量连续梁进行曲轴强度计算。计算时，以5个曲柄滑块击鼓代替五缸压裂泵，在5个曲柄中，相邻2个曲柄有一个相差144°的相位角系。

2.1 曲轴支反力及支座弯矩计算

该曲轴是一个超静定系统，因此采用三弯矩方程求解曲轴支撑处的内弯矩，进而求出支反力。如图3所示。

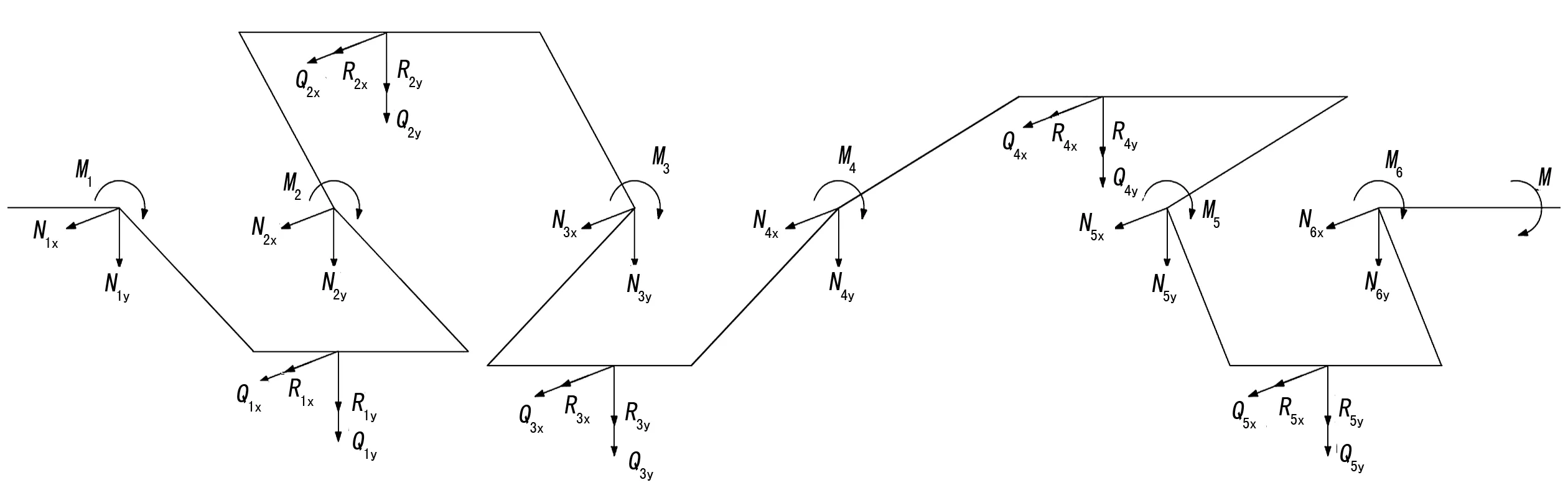
图3 曲轴受力简图

下式为支撑处内弯矩计算公式，依据下式可以分别求出支撑处x方向和y方向的内弯矩。设第一支撑和最后一个支撑处的弯矩为零，即m1=m6=0。

8mi-1+32mI+8mi+1=3(Qi-1+QI)L0

式中：QI为第i个连杆力的水平分量或垂直分量；L0为相邻轴承中心间距。

支反力求解公式如下:

左端支座：

右端支座：

式中：Ri-1为第i-1个曲拐处的旋转惯性力。

2.2 曲轴圆角应力计算

曲轴圆角是曲轴应力集中严重的部位，该部位应力较其他部位增加明显，这种应力的局部提高经常会导致曲轴圆角发生疲劳破坏。因此需要对曲轴圆角去进行校核。

(1) 名义应力计算

各个圆角处的弯矩，由下式计算：

mbi=nix×a1+mix

圆角处扭矩计算：

mti=niy×a1+Miy

进一步可以计算出圆角弯曲应力及扭转应力

弯曲应力计算公式如下：

σimax=mbimax/Wb

σimin=mbimin/Wb

式中：Wb为曲柄抗弯截面模量：

式中：d为曲柄截面直径。

计算结果如表1所列。

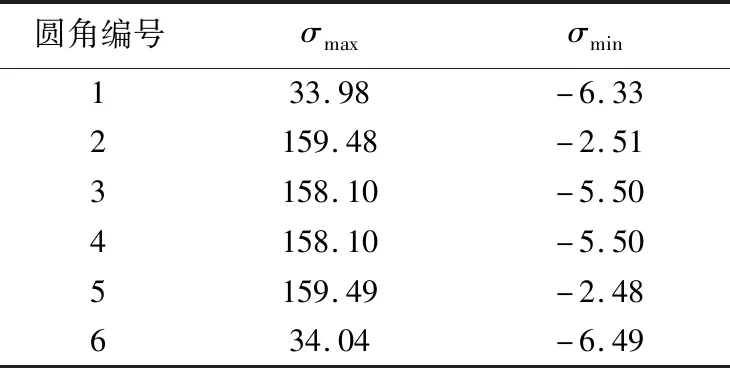
表1 曲轴圆角弯曲应力 /MPa

扭转应力计算公式如下：

τimax=Mtimax/Wt

τimin=Mtimin/Wt

式中：Wt为曲拐抗扭截面模量，Wt=πd3/16；d为曲柄截面直径。

计算结果如表2所列。

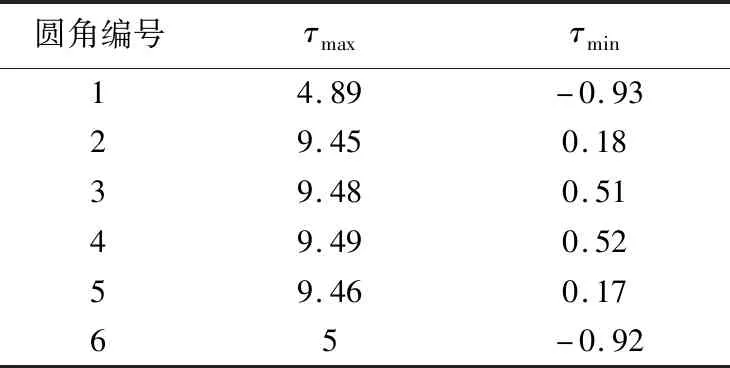
表2 曲轴圆角扭转应力、应力幅和平均应力/MPa

由表1和表2可以看出，曲柄3左侧圆角5的工况最恶劣，因此只校核圆角5是否满足强度要求。

2.3 曲轴强度校核

弯曲安全系数：

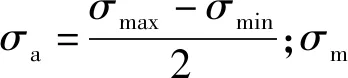
扭转安全系数：

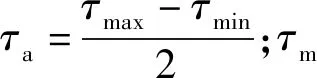
总的安全系数：

许用安全系数[n]=2.1，n>[n]。

因此，曲轴设计满足强度要求。

3 曲轴有限元分析

3.1 计算工况

采用1.2.4连杆力Q计算公式，按照每5°一个转角位置计算连杆力Q，表3列明了连杆受力最大的三个位置及连杆力大小，后续对曲轴进行三个工况的有限元强度分析计算。

表3 125°、270°和340°工况载荷大小

3.2 建立计算模型

此次计算采用SolidWorks建立三维实体模型，用Simulation 进行有限元分析。如图4所示为曲轴的三维模型。坐标系方向显示于左下方，即x轴方向沿着曲轴的轴线方向，y轴沿I拐的偏心方向，z轴则垂直于I拐的偏心方向。对曲轴三维模型进行网格划分，曲柄圆角处采用细化的网格，其余部位采用默认单元尺寸设置，按自由网格进行划分，得到曲轴的有限元模型，如图5所示。

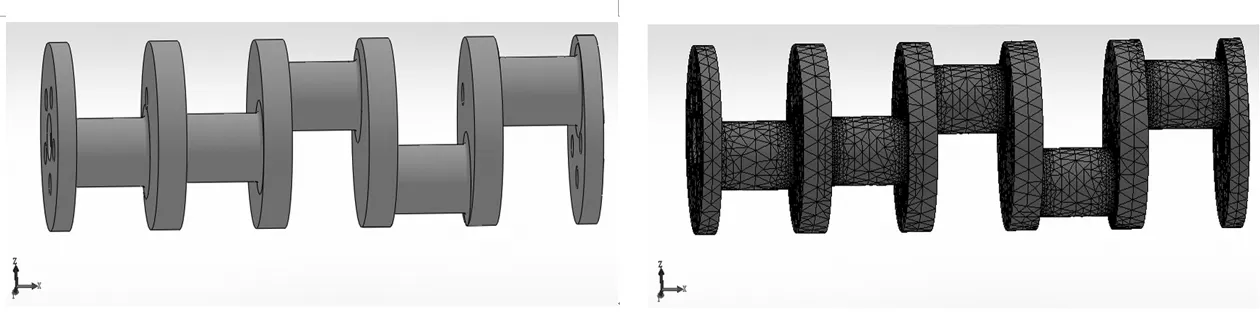
图4 曲轴三维模型 图5 曲轴有限元模型

3.3 施加载荷及约束

载荷：在SolidWorks Simulation中使用轴承载荷，在曲柄上施加沿连杆方向的连杆力,对曲轴整体施加重力加速度。

约束：使用轴承支撑，在花键一侧轴承支撑处施加刚性轴承支撑，其余五个支撑采用柔性轴承支撑，只限制曲轴的径向位移。如图6～8所示。

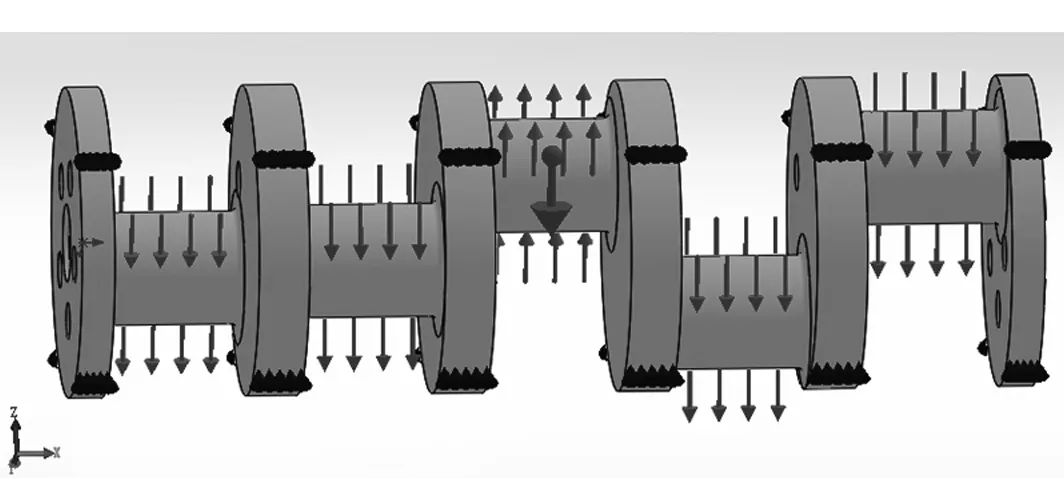
图6 125°工况施加载荷约束

图7 270°工况施加载荷约束

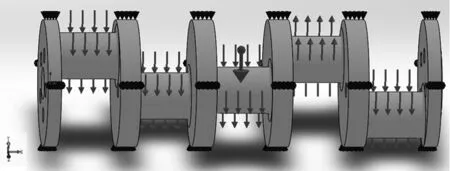
图8 340°工况施加载荷约束

3.4 计算结果分析

经过计算得到应力分布如图9～11所示。

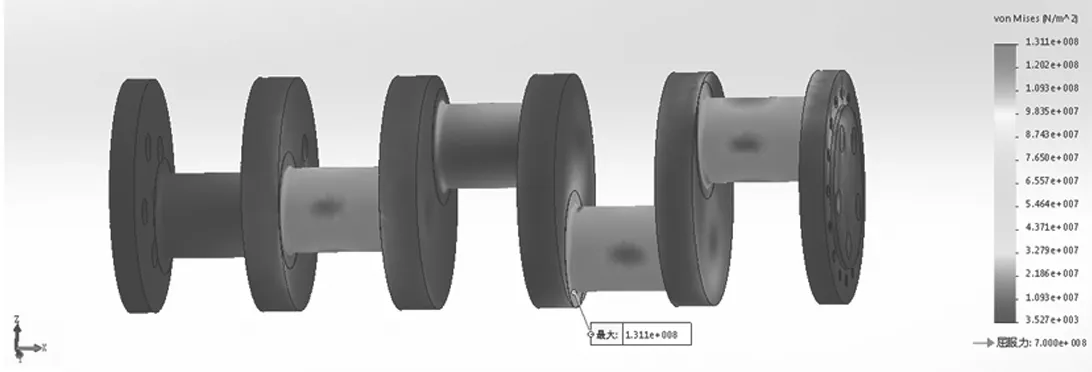
图9 125°工况vonMises应力云图

图10 270°工况vonMises应力云图

图11 340°工况vonMises应力云图

根据三种工况下曲轴的静力分析，可知曲轴曲拐同一位置，吸入工况(125°工况)与排出工况(270°工况、340°工况)相比应力很低，这一点与实际相符。125°工况时最大应力为131.1 MPa，位于第四个曲拐圆角处；270°工况时最大应力为148.9 MPa，位于第三个曲拐圆角处；340°工况时最大应力为129 MPa，位于第五个曲拐圆角处；且连杆对曲轴曲拐施力越大，曲拐所受应力越大。三种工况最大应力均位于曲拐圆角处，表明该部位应力较其他部位明显增加，这种应力的局部提高是导致曲轴圆角发生疲劳破坏的主要原因。在生产实际中，整体曲轴的断裂，多数情况下首先是在曲柄圆角出现疲劳裂纹，随后裂纹扩展导致曲轴断裂。因此，计算结果与生产实际相吻合。

曲轴材料为42CrMo，许用应力[σ]=207 MPa，有限元分析得到的最大应力为148.9 MPa，小于207 MPa，因此，该曲轴满足强度要求。这与前述采用连续梁法计算的结果是一致的。通过变换计算方法，最终得到如下结论：该曲轴满足强度要求。

4 结 论

通过对压裂泵进行连续梁法与有限元分析方法的对比计算，发现采用有限元法计算得到的曲轴危险截面应力比连续梁法的计算结果低7%，为充分发挥曲轴的潜力，应充分考虑这两种计算方法的差别。连续梁法模型中曲拐的个别力学参数需要实验确定，这种方法不能应用于曲轴设计阶段；本文有限元方法加载时对曲柄上施加沿连杆方向的连杆力，较其他学者将加载按照载荷沿曲拐轴颈轴线的方向均布或抛物线分布，沿曲拐轴颈径向方向120°角的范围按余弦分布更为接近实际工况。同时，两种计算方法都表明曲柄的圆角处是曲轴最危险的部位，在机械加工过程中，应尽量保证加工质量，也可以通过增大圆角减小应力集中。该有限元分析结果为压裂泵曲轴的科学设计提供了理论依据。