基于残差梯度法的神经网络Q学习算法

司彦娜，普杰信，臧绍飞

河南科技大学 信息工程学院，河南 洛阳 471023

1 引言

强化学习是一类介于监督学习与非监督学习之间的机器学习算法，其学习机制灵感来源于人类的学习行为[1]。它通过不断试错累积经验达到学习目的，特别适用于缺少先验知识或高度动态化的优化决策问题，因此被广泛应用在机器人控制[2]、资源优化调度[3]、工业过程控制[4]等领域，并取得了令人瞩目的成果。

经典的强化学习过程中，状态和动作空间都是离散且有限的，通常用表格来存储，值函数也需要通过“look-up table”来获得。然而，实际应用中，多数问题都具有大规模离散或连续状态（动作）空间。若使用查表法，算法的时间和空间复杂度随维数增加而成指数增长，易造成维数灾难（curse of dimensionality）问题。为了解决这个问题，一个比较好的方法就是先对值函数进行参数化表示，然后利用逼近器拟合，称为值函数近似（Value Function Approximation，VFA）方法[5-7]。常见的函数逼近器包括：线性多项式、决策树、最小二乘法和人工神经网络等。

近年来，对于各种神经网络与强化学习相结合的理论和应用研究层出不穷，例如：文献[8]针对连续状态空间强化学习问题，提出了一种基于自适应归一化RBF网络的协同逼近算法——QV(λ)，该算法对由RBFs 提取得到的特征向量进行归一化处理，并在线自适应地调整网络隐藏层节点的个数、中心及宽度，可以有效地提高逼近模型的抗干扰性和灵活性。文献[9]考虑连续状态马尔科夫决策过程，提出了一种基于极限学习机（Extreme Learning Machine，ELM）的最小二乘时序差分算法，在旅行商问题和倒立摆实验中均能用较少的资源获得较高的精度。文献[10]和文献[11]讨论了基于神经网络的强化学习算法在移动机器人导航中的应用，分别实现了移动机器人的避障和跟踪控制。

然而，对于上述多层前馈神经网络等非线性逼近器，在权值更新过程中若使用直接梯度法，已经被证明在某些条件下无法收敛[12]。若使用残差梯度法，虽然能够保证较好的收敛特性，但部分情况下的收敛速度较慢[13]。基于此，本文提出一种基于残差梯度法的神经网络Q学习算法。利用残差梯度法和经验回放机制，对神经网络的参数进行小批量梯度更新，有效减少迭代次数，加快学习速度，同时引入动量优化，进一步提高学习过程的稳定性。此外，本文选择Softplus 激活函数代替常用的ReLU 激活函数，避免了ReLU 函数在负数区域值恒为零所导致的某些神经元可能永远无法被激活，相应的权重参数可能永远无法被更新的问题。最后，利用CartPole 控制任务，对所提算法的正确性和有效性进行仿真验证，并与其他算法进行对比，结果表明本文所提算法具有良好的学习效果。

2 Q学习

强化学习中，智能体（Agent）观察当前状态（State），采取某种行为（Action）作用于环境（Environment），然后获得奖赏（Reward），并迫使环境状态发生改变，如此循环。通过与环境的不断交互，Agent 根据奖赏值随时调整自己的行为，以获得最大回报为目标，其基本原理如图1所示。

图1 强化学习基本原理

通常，回报值定义为奖赏值的加权累积：

其中，γ∈ ( 0,1) 为折扣因子，用来平衡短期奖励和长期奖励。

为了更好地描述累积回报这一变量，定义其在状态s处的期望为状态值函数（value function）：

相应地，状态-动作值函数为：

Agent 在每次动作完成以后，都要更新值函数。针对不同的更新规则，产生了多种强化学习算法。其中，Q-learning 是时序差分（Temporal Difference，TD）强化学习算法的一种，通过不断改善特定状态下特定动作的价值评估实现，相当于动态规划的一种增量方法。其更新公式定义为：

3 基于残差梯度法的神经网络Q学习算法

3.1 前馈神经网络

前馈神经网络（Feedforward Neural Network，FNN）是最常见的神经网络结构之一，较为常用的前馈神经网络有两种，一种是反向传播神经网络（Back Propagation Neural Networks，BPNN）；一种是径向基函数神经网络（Radial Basis Function Neural Network，RBFNN）。前馈神经网络的结构并不固定，以图2为例，包括输入层、一个隐藏层和输出层。层与层之间单向连接，层间没有连接；每层节点数不固定，可根据需要设置。

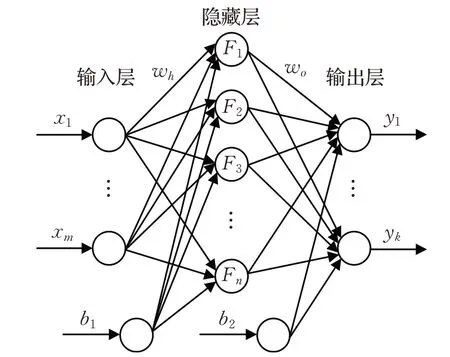
图2 前馈神经网络结构

虽然神经网络强化学习的理论研究和实际应用均取得了不错的发展，但神经网络的选择和训练依然值得关注。尤其是随着神经网络深度的增加，模型的训练也更加困难。其中激活函数是人工神经网络实现非线性逼近的关键，直接影响到网络最终的训练效果。Sigmoid函数及Tanh 函数曾经是广泛使用的一类激活函数，但这类函数包含指数运算，计算量比较大，影响学习速度，并且其饱和性导致的梯度消失现象，非常不利于深度网络的训练，已很少使用。为了解决Sigmoid 类函数带来的问题，有学者提出了线性整流单元（Rectified Linear Unit，ReLU）。ReLU 具有线性、非饱和形式，既能提高运算速度，又能缓解梯度消失现象。但是，ReLU在负数区域梯度为零，可能导致某些神经元完全不被激活，相应的参数可能永远不被更新。因此，本文采用Softplus激活函数代替ReLU。Softplus 函数可以看作是ReLU的改进版本，更加接近生物学激活特性，可以有效克服“Dead ReLU Problem”，并使整个系统的平均性能更好[14]。四种激活函数的图像如图3所示。

图3 激活函数图像

3.2 值函数近似

在离散状态或小规模强化学习问题中，值函数一般采用表格形式存储。面对大规模离散或连续状态（动作）空间问题，若使用查表法，存在维数灾难问题。因此需要采用值函数近似方法。利用神经网络对值函数进行逼近时，可表示为：

此时，w为网络更新参数。当网络结构确定时，w就代表值函数。

采用图2 所示的多层前馈神经网络逼近状态——动作值函数Q(s,a)，输入为系统状态变量，输出为每一个可能动作所对应的Q值。隐藏层有n个神经元，激活函数为Softplus 函数，记为φ(x)=ln(1+ex)，则神经网络的输出可表示为：

若按照直接梯度法，则神经网络的权值更新为：

其中，α为学习速率。

虽然直接梯度法更新过程中所需信息较少，学习速度相对较快，但其收敛性无法保证。为了保证学习过程收敛，故选择残差梯度法更新神经网络的权值。记误差函数为：

则神经网络的权值按照残差梯度法更新为：

根据目标函数更新时采用的数据量，梯度下降法大致可以分为两种：批量梯度下降算法（Batch Gradient Descent，BGD）和随机梯度下降算法（Stochastic Gradient Descent，SGD）。BGD每次更新需要对全部的训练集样本计算梯度，可以保证更新朝着正确的方向进行，最后能够收敛于极值点（凸函数收敛于全局极值点，非凸函数可能会收敛于局部极值点），但是运算量大，尤其是样本数量较多时，会导致收敛速度非常慢，且不能实时更新。SGD 每次仅随机选择训练集中的一个样本来进行梯度更新，学习速度较快，但每次更新不能保证按照正确的方向进行，并且很不稳定，容易造成优化波动，使得整体收敛速度变慢。

因此本文采用经验回放机制，储存在线学习过程中产生的样本，进而实现对神经网络参数的小批量梯度更新。该方法相较于BGD，有效减少计算量，加快学习速度；相较于SGD，大大减少迭代次数，同时训练过程更稳定。然而其收敛性受学习率的影响，如果学习率太小，收敛速度会很慢；如果太大，误差函数就会在极小值处不停地振荡甚至偏离。故而引入动量修正项，以缓解随机梯度带来的优化波动问题并加快收敛过程。动量项的加入，可以使得更新速度在梯度方向不变的维度上变快，而在梯度方向有所改变的维度上变慢，这样就可以加快收敛并减小振荡[15]。

引入动量的梯度下降法更新公式为：

4 仿真实验

4.1 问题描述

CartPole控制是测试强化学习算法性能的常用任务之一。如图4 所示，在游戏里，一根杆子由一个非驱动性关节连接到一个小车上，小车可以沿着无摩擦的轨道移动。游戏开始，杆子是直立的，通过对小车施加+1或-1 的力来控制小车前后移动。每次动作，若杆子保持直立，奖励值为+1，若杆子离开垂直方向超过12°，或者小车距离中心移动超过2.4个单位，游戏结束。

图4 CartPole模型示意图

该系统中，状态为水平方向的位置及导数和垂直方向的偏角及导数属于连续变量；动作为离散变量A=[-1,1]，分别表示向左或向右移动。实验使用图2所示神经网络结构，隐含层神经元个数设为200。

4.2 实验结果与分析

为了充分验证所提算法的正确性和有效性，进行两组对比实验。实验中，动作选择使用ε-greedy 策略，并且为了平衡探索和利用的关系，每一轮游戏中，ε逐渐减小，探索值ε=(0.9 →0.01) 。其他参数设置为：折扣因子γ=0.9，学习率η=0.001，动量衰减值μ=0.5，批量大小batch_size=32。

实验1 分别对比随机梯度下降（SGD），小批量梯度下降（MBGD）和本文所提算法在ReLU 和Softplus 两种激活函数下的单轮学习得分情况，结果如图5所示。

图中，横坐标Episode表示游戏进行的轮数，纵坐标Reward 表示每轮游戏结束获得的奖励。每幅图中，左侧为ReLU 激活函数训练下的结果，右侧为Softplus 激活函数训练下的结果。

其中，图5（a）的SGD 算法在ReLU 激活函数下，虽然200 轮以后，可以达到最高分，但在1 000 轮结束后，每轮游戏的得分波动依然很大；而使用Softplus 激活函数，在大约200轮以后，得到最高分的次数逐渐增多，并且分数基本保持在75 分以上。图5（b）的MBGD 使用ReLU在100轮左右得到最高分，但大概在600轮以后分数才基本稳定在175 分以上；而使用Softplus 激活函数在100 轮左右得到最高分，500 轮以后分数的波动次数就明显减少，基本能够得到最高分。图5（c）本文所提算法在两种激活函数训练下，均在100轮左右开始取得最高分，但使用ReLU 在后续训练过程中分数不太稳定，仍然存在相对较多的波动；使用Softplus 激活函数大约200轮之后基本维持在最高分，只有几次小幅度的分数波动。

图5 CartPole任务单轮得分

横向对比，三种算法在使用Softplu函数代替ReLU函数以后，分数波动大幅减小，而得到最高分的次数明显增多，训练效果得到显著提高。纵向对比，在两种激活函数训练下，本文所提出的基于动量修正的MBGD算法比常规的SGD算法和MBGD算法能更多地得到最高分，且分数波动次数与波动幅度均得到有效抑制。

实验2 在Gym 中，CartPole 任务设定每个episode最大步数为200，并规定每100 个episode 的平均奖励若超过195，则视为训练成功。所以，本组实验将对比本文所提算法与另外两种算法的训练成功率。

对比算法选择常规的随机梯度下降法（SGD with ReLU）和小批量梯度下降法（MBGD with ReLU）。为了尽可能获得有效数据，每种算法实验4 次，并且实验过程中保持其他参数不变。设置episode 为3 000，每100个episode记为一次训练，取其平均奖励值作为训练结果，则三种算法的最终任务完成效果如图6 所示，统计结果见表1。其中，图6为三种算法在4次实验中的训练平均得分分布，表1为训练成功次数统计。

实验结果表明，ReLU 激活函数情况下：SGD 算法4 次实验均未成功；MBGD 算法最少成功19 次，最多成功26次，成功率在63%以上。而本文提出的算法，最少成功26次，最多成功28次，成功率在86%以上。对比图6（b）和6（c），可以看出本文所提算法表现更加稳定，失败情况相对较少，且集中在训练初始阶段，5次之后，基本能够保持成功，且稳定在最高分。

表1 CartPole任务成功次数统计表

图6 CartPole任务平均得分

5 结论与展望

本文针对具有连续状态空间的强化学习问题，提出了一种基于残差梯度法的神经网络Q 学习算法。首先利用多层前馈神经网络实现了Q值函数的近似表达，然后采用残差梯度法和经验回放机制，对神经网络的权重参数进行小批量梯度更新，加快了学习速度；动量优化的引入，提高了训练过程的稳定性。此外，Softplus函数代替一般的ReLU 激活函数，避免了ReLU 函数在负数区域值恒为零所导致的某些神经元可能永远无法被激活，相应的权重参数可能永远无法被更新的问题。最后，CartPole 任务的实验证明，在同等条件下，本文所提算法能够在更少的训练次数下完成任务，并且得分更高，表现更加稳定。

然而，神经网络等非线性函数逼近缺乏可靠的收敛性保证，且泛化性能较差。接下来需要考虑本文算法在其他控制任务中的表现，并进一步提高时效性。