逆半群同余的对偶刻画

赵雪欣，陈芬芬，高连飞，谢祥云

（五邑大学 数学与计算科学学院，广东 江门 529020）

Vagner[1]在1952年首次提出逆半群理论，随后Preston[2-4]也提出这个概念.Vagner[5]最初把逆半群称为“广义群”，无论是Vagner还是Preston，最初提出逆半群的动机是研究集合上的部分一一映射所构成的半群.逆半群最早的结果之一是表示定理（类似于群论中的Cayley定理），即每个逆半群都具有忠实表示作为部分一一映射的逆半群.

由于逆半群的理论与群的理论有许多相似之处，所以促使了很多学者对逆半群上的同余关系进行研究学习，特别是核—迹方法对同余的刻画.1961年，Munn[6]首次提出逆半群的同余σ ，并给出其刻画；1964年Howie[7]给出了最小群同余和最大幂等分离同余的刻画；1966年Lallement[8]给出对μ=Hb的研究.1974年Scheiblich[9]首次提出核与迹；1975年和1978年Green[10]和Petrich[11]也对其做了更深入的研究.1981年Petrich和Reilly[12]将相同的想法应用于完全单半群.

本文基于Petrich[11]和Howie[7,13]对逆半群核迹同余的研究，给出了核迹同余的一种对偶刻画，并在此基础上研究了S 上的最小群同余和最大幂等分离同余的相应理论和性质.

1 预备知识

本节的基本知识主要来源于文献[13].在一个半群S 中，定义Green 关系如下：

设a∈S ，元素a 称为正则的，如果存在x∈S ，使得axa=a.如果S 中每一个元素都是正则的，则S 称为正则的.半群S 称为逆半群如果S 中每个元均有逆元存在且幂等元可交换.

引理1[13]145设S 是一个半群，则下列命题等价

1）S 是一个逆半群；

2）S 是正则的，并且它的幂等元可换；

3）每一个L 类和每一个R 类只包含一个幂等元；

4）S 中的每一个元素有唯一逆元.

引理2[13]146设S 是一个逆半群，E (S) 是其幂等元构成的半格.那么

1）对任意 a,b∈S，(ab)-1=b-1a-1；

2）对任意a∈S，e∈E (S)，aea-1和 a-1ea都是幂等元.

设ρ 是逆半群S 上的一个同余关系，E (S)是S 的幂等元构成的半格.ρ 限制在 E (S)上是 E (S)的一个同余关系，我们称为ρ 的迹，写作 τ=tr ρ.每一个 τ类e τ等于 eρ ∩E (S).同余关系 τ称作正规的，如果 e τf ⇒(∀ a∈S)a-1ea τa-1fa.我们知道，设ρ 是逆半群S 上的一个同余关系，那么S/ρ是一个群当且仅当tr ρ=E (S)×E (S).

设ρ 是逆半群S 上的同余关系，S 的幂等元集是 E (S)，那么ρ 的核定义为文献[13]中已经证明逆半群S 的核N 是S 的完全逆子半群且是正规的，且核Ker ρ 与迹tr ρ 有如下关系：

若N 是S 上的正规子半群，τ是 E (S) 上的正规同余，则S 上的同余对(N,) τ定义如下[13]：

定理1[13]157设S 为逆半群，E (S) 是S 上幂等元构成的半格，若ρ 为S 上的同余，则(ker ρ,tr)ρ是一个同余对；

本文主要内容是在定理1 的基础上给出它的对偶定理.

2 主要结果

在给出定理1 的对偶刻画之前，我们有以下关于同余对的对偶定义：

定义1S 是一个逆半群，E (S)是S 上幂等元构成的半格.设N 是S 上的正规子半群，τ是E (S)上的正规同余，称(N,τ)是S 的一个同余对如果满足条件：对任意的a∈S和 e∈E (S)，有

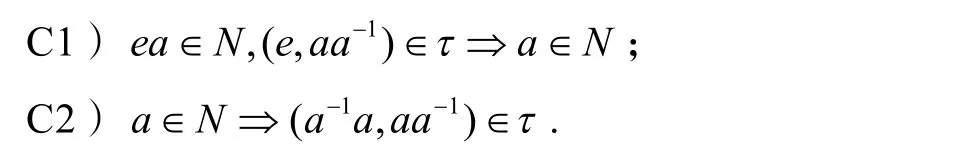
引理3设S 是一个逆半群，E (S)是S 上幂等元构成的半格，ρ 是S 上的一个同余，则对任意的a∈S，e∈E (S)，有

证明1）设 ea ρ f，f∈E (S)，因为 (a=aa-1a) ρ ea ρf ，所以a∈kerρ.

2）设a∈eρ，e∈E (S)，显然有 a-1∈eρ，于是有 a-1a,aa-1∈eρ，则 (a-1a,aa-1)∈tr ρ.

引理4设S 是一个逆半群，(N,τ)是S 的一个同余对，则对于任意的 a,b∈S，e∈E (S)，有

1）若bea∈N，e τaa-1，则ba∈N.

2）若 (aa-1,bb-1)∈τ，a-1b∈N ，则对 每个 e∈E (S)，有 (aea-1,beb-1)∈τ.

证明1）设bea∈N，e τaa-1，则 bea=bb-1b ea=beb-1b a=f (ba)∈N ，其中 f=beb-1∈E (S).因为(f=beb-1) τ(b aa-1b-1=ba (b a)-1)，所以根据定义1 的C1），有ba∈N.

2）设 (aa-1,bb-1)∈τ，a-1b∈N ，则(mod τ)有

所以，(aea-1,beb-1)∈τ.

下面我们给出定理1 逆半群同余的对偶刻画：

定理2设S 为逆半群，E (S) 是S 上幂等元构成的半格，若ρ 为S 上的同余，则(ker ρ,tr)ρ 是一个同余对；

反之，若(N,τ)是一个同余对，则关系 ρ(N,τ)={(a,b)∈S :(aa-1,bb-1)∈τ,a-1b∈N}是S 上 的 一 个 同余.此 外 ker ρ(N,τ)=N ，tr ρ(N,τ)=τ，ρ(kerρ,trρ)=ρ.

证明"⇒".若ρ 为S 上的同余，则由引理3，(ker ρ,tr ρ)是一个同余对.

" ⇐".设(N,τ)是一 个同余 对，ρ(N,τ)={(a,b)∈S :(aa-1,bb-1)∈τ,a-1b∈N}.因为N 是S 上的 正规子半群，τ是 E (S)上的正规同余，所以ρ 是自反的和对称的.要证ρ 是传递的，只需证明对任意的(a,b)∈ρ，(b,c)∈ρ，有(a,c)∈ρ.

设(a,b)∈ρ，(b,c)∈ρ，则由 (aa-1,bb-1)∈τ，(b b-1,cc-1)∈τ，有 (aa-1,cc-1)∈τ.因为 a-1b,b-1c∈N，于是有 a-1(b b-1)c=a-1ec∈N ，e=bb-1.由于 (b b-1=e) τcc-1，根据引理4 1），有 a-1c∈N ，所以(a,c)∈ρ.因此ρ 是一个等价关系.

要证ρ 是一个同余关系，只需证明

设(a,b)∈ρ，则有 (aa-1,bb-1)∈τ，a-1b∈N ，根据引理4 2），有

因为N 是正规的，所以有 (ac)-1bc=c-1(a-1b)c∈N ，因此(ac,bc)∈ρ.又因为

所以(ca,cb)∈ρ.因此，ρ=ρ(N,τ)是S 上的一个同余关系.

若a∈eρ，e∈E (S)，则 e τaa-1，ea∈N，根据定义1 C1），有a∈N.因此，kerρ⊆ N.反之，若a∈N，则 e-1a=ea∈N ，e=aa-1；由幂等元 ee-1=aa-1有ee-1τaa-1，所以 a∈eρ⊆ kerρ.因此，ker ρ(N,τ)=N.

设 e,f∈E (S)，若 (e,f)∈ρ=ρ(N,τ)，则 (e=ee-1) τ(f f-1=f)，因此tr ρ⊆ τ.反 之，若 e τf，则(e e-1=e) τ(f=ff-1)，e-1f=ef∈E (S)⊆ N ，所以 (e,f)∈ρ∩（E (S)×E (S)）=trρ.因此 tr ρ(N,τ)=τ.

设(a,b)∈ρ，则 (a-1,b-1)∈ρ，于是有 (aa-1,bb-1)∈ρ.因为 aa-1，bb-1是幂等元，所以有(aa-1,bb-1)∈tr ρ.由于 (a-1b,b-1b)∈ρ，则有 a-1b∈(b-1b)ρ⊆ ker ρ，因此 ρ⊆ρ(kerρ,trρ).反之，设(a,b)∈ρ(kerρ,trρ)，则有 (aa-1,bb-1)∈tr ρ，a-1b∈kerρ.因为 (a-1b)ρ是 S /ρ 的一个幂等元，所以于是有

因此(a,b)∈ρ，故 ρ=ρ(kerρ,trρ).

性质1设S 是一个逆半群，E (S)是S 上幂等元构成的半格，令 τ是 E (S)上的正规同余，然后有：

2）关系 τmax={(a,b)∈S×S :(∀ e∈E (S)) aea-1τb eb-1}是S 上以 τ为迹的最大同余.

证明仿照文献[13]中相关定理的证明，省略.

推论1若 τ=E×E ，则 τmin={(a,b)∈S×S :(∃ e∈E (S)) ae=be}.

一般地，记 σ=τmin，称为S 上的最小群同余，则S /σ 是S 上的最大群同态像.于是，对于S 上使得 S /γ 是一个群的每一个同余γ ，都存在一个同态 ζ:S/σ→ S/γ.容易验证，σ 的核如下：

定理3设S 是一个逆半群，E (S)是S 上幂等元构成的半格，令σ 是S 上的最小群同余，则ker σ=Eω，且 σ={(a,b)∈S×S:a-1b∈Eω }.

一个同余称为幂等分离，如果它的迹是恒同余1 的.根据性质1 2），我们有以下推论：

推论2若 τ=1E，则 τmax={(a,b)∈S×S :(∀ e∈E (S)) aea-1=beb-1}.

一般地，记 μ=τmax，称为S 上的最大幂等分离同余.要确定ker μ ，我们需要一个定义：在S 上设 E (S)的中心化子为Eς ，其中 Eς={a∈S :(∀ e∈E (S)) ae=ea}.然后有下面的结论：

定理4设S 是一个逆半群，E (S)是S 上幂等元构成的半格，令μ 是S 上的最大幂等分离同余，则ker μ=Eς，且 μ={(a,b)∈S×S:aa-1=bb-1,a-1b∈Eς }.

下面给出μ 的进一步刻画：

性质2设S 是一个逆半群，E (S)是S 上幂等元构成的半格，令μ 是S 上的最大幂等分离同余，则 μ=Hb为S 上包含在H 里的最大同余.

证 明设(a,b)∈μ，则由定理4得 aa-1=bb-1.因为 (a-1,b-1)∈μ，所以有 a-1a=b-1b ，因此(a,b)∈H，μ⊆ H.下面证明μ 是S 上包含在H 里的最大同余.考虑S 上的任意一个同余ρ ，且ρ⊆ H.假设(a,b)∈ρ，则 (a-1,b-1)∈ρ，于是对任意的 e∈E (S)，有 (aea-1,beb-1)∈ρ⊆ H.由S 上的每个H 类最多包含一个幂等元可知，对任意的 e∈E (S)，有 aea-1=beb-1，因此(a,b)∈μ.

一个逆半群S 称为基本的，如果在S 上的最大幂等分离同余是恒同余1S的.

定理5设S 是一个逆半群，E (S) 是S 上幂等元构成的半格，令μ 是S 上的最大幂等分离同余，则 S/ μ 是基本的，且 S/ μ 上的幂等元所构成的半格与 E (S) 同构.