分形集上关于扰动的梯形积分公式的Iyengar 型不等式
2020-09-15曾志红时统业
曾志红,时统业
(1.广东第二师范学院 学报编辑部,广东 广州 510303;2.海军指挥学院,江苏 南京 211800)
1 引言与预备知识
梯形不等式[1]是

其 中 f:[a,b]→R 在(a,b)内 二阶 可 微且有关梯形不等式和扰动的梯形不等式可参阅文献[2-6].
Iyengar 不等式[7]是

其中 f:[a,b]→R 是[a,b]上的可微函数,且存在常数M ,使得对任意 x∈[a,b]有有关Iyengar 型不等式和扰动的Iyengar 型不等式可参阅文献[8-12].
沿用文献[13]的记号,设

定理1[13]设区间I⊆R,I°是I 的内部,f: I →R 在I°上二次可微,a,b∈I°,a<b.若存在常数M2∈R,使得对于任意 x∈[a,b]有则有
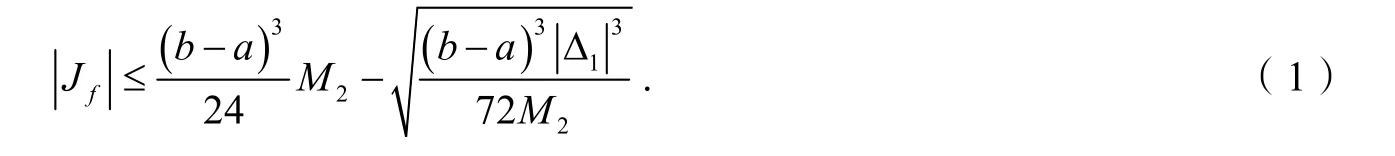
本文全篇假设0<α≤1.文献[14-15]系统阐述了建立在分形空间上的局部分数阶微积分的相关理论.设 Rα是分形实线的α 型集合,aα,bα,cα∈Rα,则在这个分形集中有如下运算律:
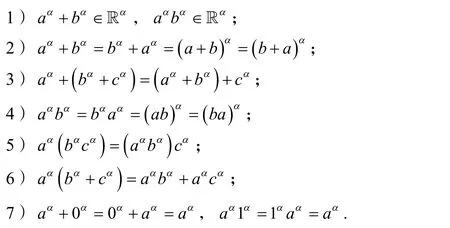
下面使用Gao-Yang-Kang 的方法来描述局部分数阶的导数和积分.
定义1[16]设 f: R →Rα是不可微函数,如果对任意ε> 0,存在δ> 0,使得当时,有则称f 在点 x0处局部分数阶连续.若f 在区间I⊆R 上局部分数阶连续,则记为f∈Cα(I).
定义2[17]设 f∈Cα(a,b),x0∈(a,b),则f 在点 x0处的α 阶局部分数阶导数定义为

若对任意x∈I⊆R 时存在 f(α)(x),则称f 在I 上α 阶局部分数阶可微,记为 f∈Dα(I).一般地,记如果对任意x∈I⊆R,存在则记为其中 k=0,1,2,….
设 f,g∈Dα(I),则对任意x∈I,有利用这个局部分数阶导数的乘法法则,有
定义3[18]设 f∈Cα[a,b],f 在点[a,b]上的α 阶局部分数阶积分定义为
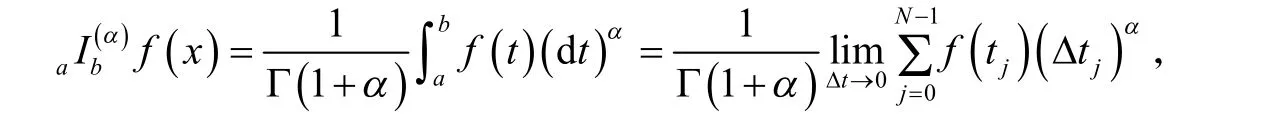
在闭区间上局部分数阶连续的函数是局部分数阶可积的.局部分数阶定积分有与黎曼定积分类似的性质,如线性性质、区间可加性、比较性质、绝对不等式、牛顿-莱布尼茨公式、换元法、分部积分法等[14-18].
引理1[18]1)设则特别地,若 f (x)恒为常数c,则有
2)设 f,g∈Dα[a,b]且则

利用引理1 得
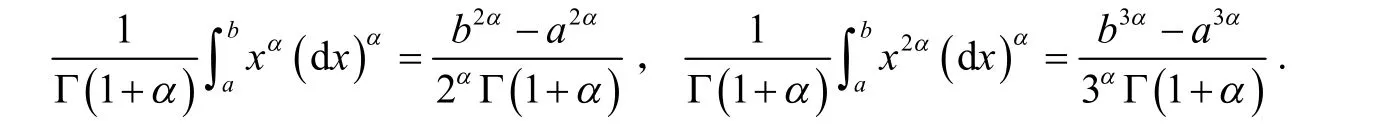
文献[19]引入分形集上广义凸函数的概念.
定义4[19]设I⊆R,函数 f :I →Rα,若对任意 u,v∈I和任意 λ∈[0,1],有

则称f 是I 上的广义凸函数.
引理2[19]设 f∈Dα(I),则下面条件等价:
i)f 是I 上的广义凸函数;
ii)对任意 x1,2x∈I ,有
引理3[19]设 f∈D2α(a,b),则f 是(a,b)上的广义凸函数当且仅当对任意 x∈(a,b)有 f(2α)(x)≥0α.本文为方便起见,记

本文目的是在分形集上建立关于扰动的梯形积分公式的不等式.为得到本文的主要结果,需要下面的引理.
引理4设区间I⊆R,I°是I 的内部,则有

证明使用局部分数阶积分的分部积分法(引理1)得

式(4)除以 2αΓ2(1+α),则式(2)得证.类似可证式(3).
引理5设区间I⊆R,I°是I 的内部,若存在常数 k,K∈Rα,使得对于任意 x∈[a,b]有 k≤f(2α)(x)≤K ,则有
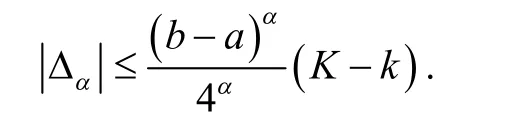
证明由式(3)得
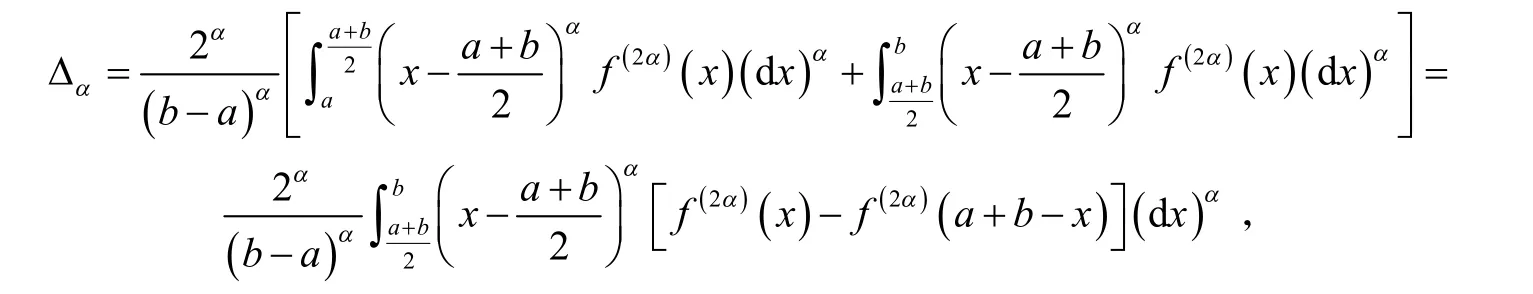
于是

引理6[17](局部分数阶微分中值定理)设函数 F (x)在[a,b]上连续,在(a,b)上α 阶局部分数阶可微,则对于任意 x0,x∈[a,b],x0<x,存在 ξ∈[x0,x],使得

2 主要结果
定理2设区间I⊆R,I°是I 的内部,若存在常数 k,K∈Rα,使得对于任意 x∈[a,b]有 k≤f(2α)(x)≤K ,则有


证明对任意常数ε ,由引理4 得

其中

当 Δα≥0时,考虑任意有

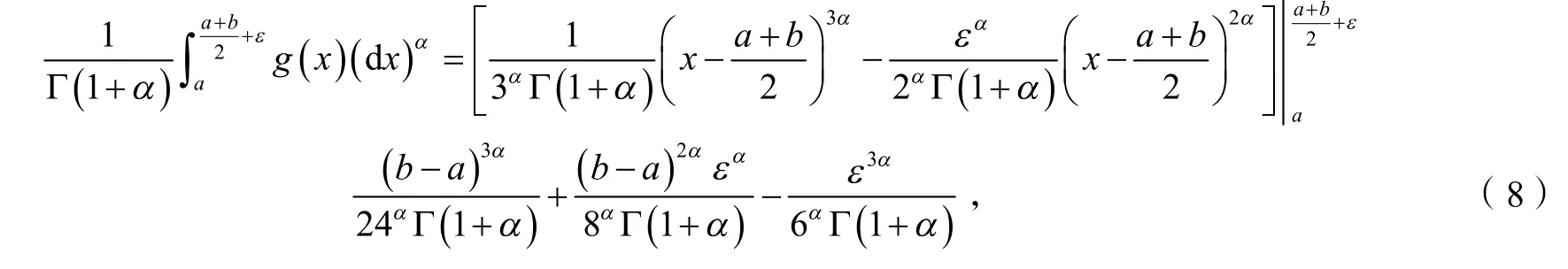
类似可得

综合式(6~10)得
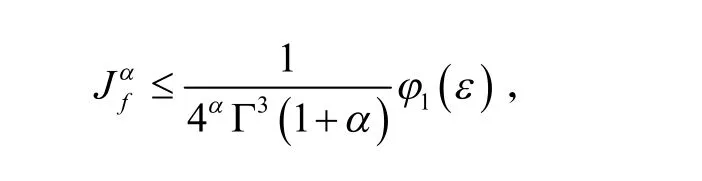
其中
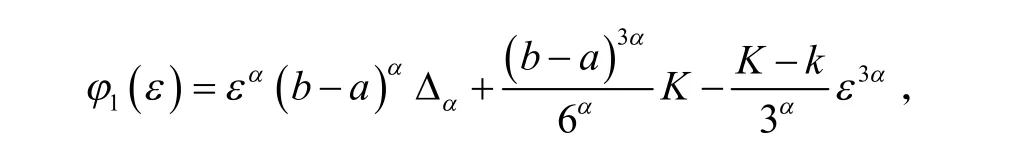
于是有



综合式(11~14),当 Δα≥0时,有

当 Δα≤0时,考虑任意
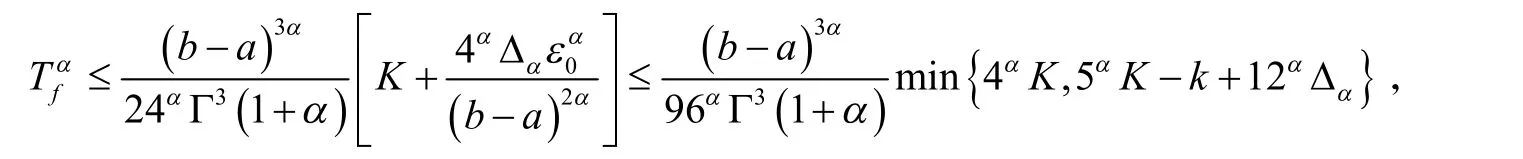
通过这些以往研究可以发现,从横向上看,对于“媒体会对政策变迁产生影响”这一观点,各学科虽论证方式不同,但已达成广泛共识;从政策学角度出发的研究不少,但充分运用理论展开主体细致分析的不多。从纵向上看,有研究已发现传统媒体与新媒体在影响政策议程、政策变迁上的差异,但缺乏理论指导下的深入比较,也未能结合当下我国媒介融合的时代背景。
推论1设区间I⊆R,I°是I 的内部,若存在常数M∈Rα,使得对于任意 x∈[a,b]有则有

证明在定理2 中取 k=-M,K=M即可得证.
推论2设f :[a,b] →R二次可微,f′在[a,b]上连续,且存在常数k 和K ,k<K使得k≤f′≤K,则有

证明在定理2 中取α=1 即可得证.
注1在推论2 中,若存在常数M2,使得则得到定理1.
定理3设区间I⊆R,I°是I 的内部,

证明利用引理3 得:
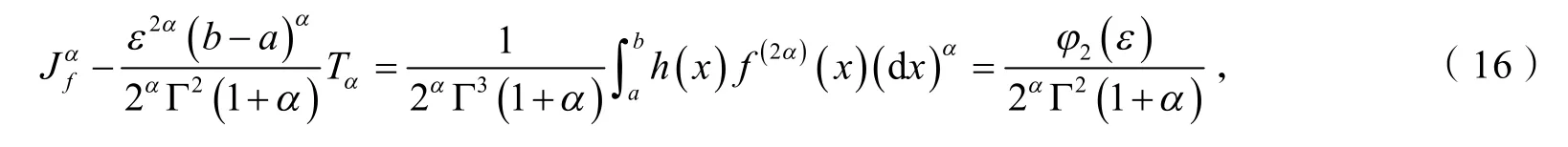
其中


综合式(16~17)得

其中

于是有

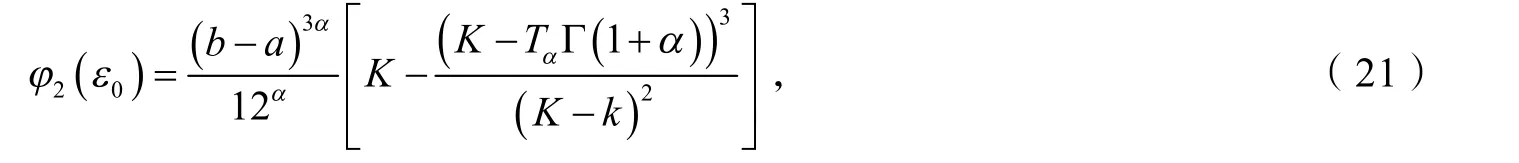
综合式(18~21),则式(15)的右边的两个不等式得证.当 k≤f(2α)≤K 时,有-K≤(-f)(2α)≤-k.对函数-f应用已证结论,则式(15)的左边的两个不等式得证.
推论3设区间I⊆R,I°是I 的内部,若存在常数M∈Rα,使得对于任意 x∈[a,b]有则有
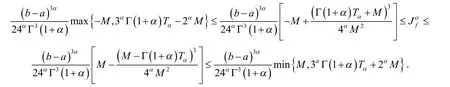
证明在定理3 中取 k=-M,K=M即可得证.
推论4设f :[a,b]→R二次可微,f′在[a,b]上连续,且存在常数k 和K ,k<K使得k≤f′≤K,则有

证明在定理3 中取α=1 即可得证.
注2在推论4 中,若存在常数M2,使得则有

注3式(1)与式(22)各有强弱.比如取 f (x)=x4,[a,b]=[-1,1],则 M2=12,T1=4,Δ1=0,显然式(22)比式(1)好些.又比如取 f (x)=x3,[a,b]=[-1,1],则 M2=6,T1=0,Δ1=4,由式(1)得由式(22)得因为故式(1)与式(22)好些.
