一类具有Holling II 型功能反应的分数阶捕食者-食饵系统的动力学分析
2020-09-15杜争光蒲武军
杜争光,蒲武军
(陇南师范高等专科学校 数学系,甘肃 陇南 742500)
分数阶捕食系统的动力学研究是整数阶动力系统研究的拓展和延伸,是生物种群动力学研究的一个重要组成部分.Ahmed[1]讨论了一类分数阶捕食者-食饵模型,此后,分数阶种群动力学的研究逐渐成为了一个热点课题,受到了许多学者的广泛关注,取得了一系列好的研究成果[2-5].Komeil[6]讨论了一类具有Holling II型功能反应的捕食系统,对平衡点的稳定性进行了研究,并证明了分数阶种群动力学模型平衡点的稳定性、收敛速度与系统的阶数α 密切相关.Khoshsiar[7]对一类食饵具有非线性收获的分数阶捕食模型进行了研究,并指出,分数阶模型表现了更加丰富的动力学行为,且随着分数的阶的改变,动力学行为会越来越复杂.
目前,针对具有Holling II型功能反应的分数阶捕食者-食饵模型的研究,已经有了部分结果[5-8].本文考虑一类具有Holling II型功能反应且食饵和捕食者都具有线性收获的分数阶捕食者-食饵模型:

其中,α∈(0,1]; r,k,a,b,c,d1,d2,h 均为正常数.r 表示食饵的增长率,k 表示食饵的环境容纳量,b 表示捕食率,c 表示食饵的转化率,d1,d2表示食饵和捕食者收获率,a 表示Holling II功能系数,h 表示捕食者的死亡率.u (t)和 v (t)分别表示食饵和捕食者的种群密度,初始条件 u (0)>0,v(0)>0.

1 预备知识和引理
定义1[9]设函数 f:R+→R+,且 f (x)和f(n)(x) 均连续,则其α 阶Caputo分数阶导数定义为:其中,n-1≤α<n,Γ (·) 是Euler Gamma函数.
性质1[10]Caputo分数阶导数满足线性运算性:
引理1[11]设分数阶系统有平衡 点 (xe,ye),则平 衡点 (xe,ye)局部渐近稳定的充要条件是:Jacobian矩阵在平衡点 (xe,ye)的所有特征值 λi满足条件
引理2[12]设 x(t)∈R+是连续可微函数,则对任意时刻t≥t0,有
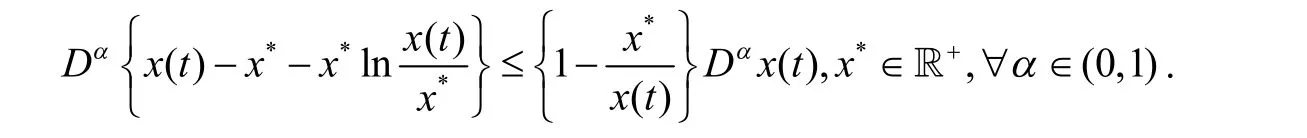
引理3[13]分数阶系统 Dαx (t)=f (t,x),t>t0,其中,f :[t0,∞)×Ω →Rn,Ω ⊂Rn,x(0)=x(t0),α∈(0,1],若函数 f (t,x) 关于x 满足局部Lipschitz条件,则系统存在[t0,∞)×Ω 上的唯一解.
引理4[14]设 u (t) 是定义在 [0t,∞)上的连续函数且满足其中λ>0 ,初始时刻 t0≥0.则Eα是Mittag-Leffler函数,即
2 主要结果及其证明
2.1 解的存在唯一性、非负性和有界性
定理1对任意初值(x (t0),y (t0))∈Ω,Ω={(x,y)∈R2:max{|x|,|y|}≤M},系统(1)存在唯一解X=(x,y)∈Ω,且对任意的初值 (x(t0),y (t0))∈Ω+,系统(1)的所有解均非负且一致有界.
证明首先,令定义映射 H (X)=(P (X),Q (X)),对

以下证明非负性和一致有界性.

因此,系统(1)始于Ω+的所有解均在上,即Γ 是关于系统(1)的正交不变集,且对任意初值 (x(t0),y (t0))∈Ω+,系统(1)的所有解均有界.
2.2 平衡点的局部稳定性
为方便说明问题,首先求出系统(1)在 E (x,y) 点的Jacobian 矩阵:

定理2系统(1)的平凡平衡点E0(0,0)和边界平衡点均不稳定.
证明易知系统(1)在E0(0,0)点的Jacobian 矩阵对应的特征值分别为 λ1=r-d1>0,λ2=-(d2+h)<0,则由引理1 知E0(0,0)不稳定.
结合条件H2,同理可得,系统(1)的边界平衡点亦不稳定.
定理3若条件 1H 和H2满足,且下列任一条件成立:

证明系统(1)在正平衡点 E2(x*,y*)处的Jacobian 矩阵为

故其特征根可表示为

若条件i)成立,则 rp+2rx*+d1-r>0,从而分两种情形:
1)若 tr2(J2)-4det(J2)≥0,则有 λ1<0,λ2<0,于是由引理1 知正平衡点 E2(x*,y*)局部渐 近稳定.
2)若 tr2(J2)-4det(J2)≥0,则 λ1和 λ2是一对共轭复根,且 Re(λ1)=Re(λ2)=tr(J2)<0,故|arg(λ1)|>由引 理1 知正平 衡点 E2(x*,y*)局部渐 近稳定.
综上,正平衡点 E2(x*,y*)局部渐 近稳定.
若条件ii)成立,则

若条件iii)成立,则

2.3 平衡点的全局渐近稳定性
定理4若条件 H1和H2满足,且 rp (p+x*)> y*,则系统(1)的唯一正平衡点 E2(x*,y*)是全局渐近稳定的.
证明定义 E2(x*,y*)处的Lyapunov 函数 V (t)如下:
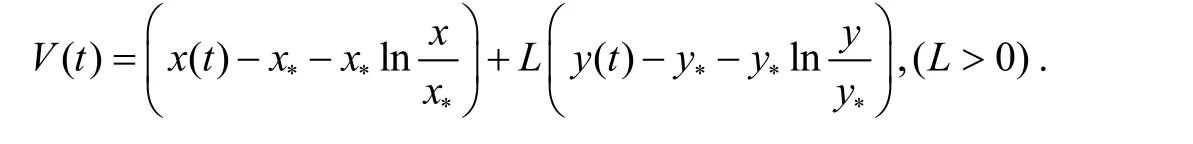
由引理2 可得:

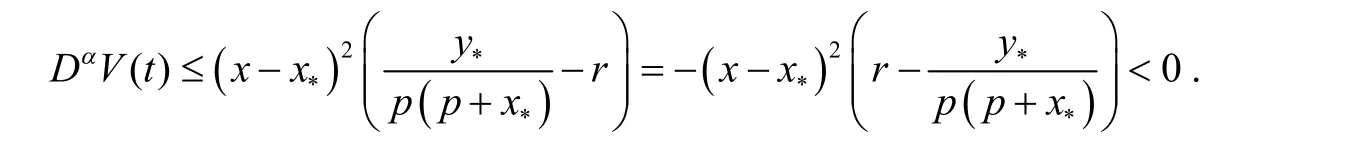
显然,平凡平衡点 E0和边界平衡点 E1均在Γ 的边界处,正平衡点 E2在Γ 内,由定理1 知集合仍然是系统(1)的一个正不变集和全局吸引集.由文献[15]知,对于任意初值条件即正平衡点2E 是全局吸引的,此即说明系统(1)的正平衡点 2E 是全局渐近稳定的.
